圆外切Bounding-box WSN定位方法

罗清华，焉晓贞，彭宇，王丹，彭喜元

(1.哈尔滨工业大学(威海)信息与电气工程学院，山东 威海264209;2.哈尔滨工业大学自动化测试与控制研究所，黑龙江哈尔滨，150080;3.通用电气公司(上海)，上海200241;4.桂林电子科技大学广西自动检测技术与仪器重点实验室，广西 桂林541004;5.地理信息工程国家重点实验室，陕西西安710054)

在Bounding-box方法中［1］，定位准确度不能随距离估计精度的提高，而持续提高［2］。针对这个问题，众多学者提出了Bounding-box的改进方法:郭海琦等人提出了三点质心定位Bounding-box和三点加权质心Bounding-box定位算法［3］，然而改善程度有限。受加权质心算法的启发，文献［4］提出了加权Bounding-box改进算法。姚英彪等人提出了采用边框定界方法来确定节点存在的区域，然后将区域网格化，并用全搜索的方法找到最佳估计点［5］，但存在计算量大的问题。Sanabria-Russo等人提出了一种灵活的定位方法，可根据应用需求来选择不同的定位方法［6］;文献［7］提出了加权的Bounding-box定位方法，但没有在实际应用环境中进行验证;文献［8］提出利用加权的最小二乘来解决室内非视距定位问题，但其计算复杂度较高。文献［9］提出基于差分修正的加权质心定位算法，从一定程度上克服距离估计误差对定位的影响。上述方法在一定程度上改善了Bounding-box算法的定位精度，然而仍存在着改善程度有限、计算量大的问题。而本文则从正方形区域和实际通信区域模型的差异区域入手，分析导致Bounding-box定位误差较大的原因，并合理运用2个模型间的误差区域，提出了圆外切的Bounding-box定位改进算法。

1 圆外切Bounding-box定位方法

在传统的Bounding-box定位算法中，为了计算简便，通信区域选择以2d为边长的正方形，其中d为未知节点与锚节点之间的距离测量值。然而，这样将导致正方形区域与实际通信圆区域之间存在误差区域。鉴于此，本文提出一种改进的Bounding-box定位方法，即圆外切Bounding-box定位算法，能够减小这类误差区域的大小，使定位估计更加准确。

在Bounding-box算法的基础上，基于圆外切的bounding-box改进算法不再采用正方形作为通信区域，而是采用圆形作为通信区域。在正方形的定位区域中，四个角分别放置一个锚节点，平移正方形的对角线使其切于各个锚节点通信区域的圆，根据对角线的不同，该直线可以表示为y=x+bi或y=－x+bi。寻找4条切线所组成的矩形区域，并将这个区域的质心作为未知节点的估计坐标，其原理如图1所示。

图1 改进的Bounding-box算法原理示意图Fig.1 The principle of improved Bounding-box

本文提出的改进方法在运算中将传统方法中寻找正方形交集区域变换为寻找切线组成的区域，从而缩小定位的估计范围，使定位精度得到提升。

基于以上思路和分析，基于圆外切的Bounding-box改进算法的具体实现步骤如下:

1)未知节点周期地广播定位请求数据包。

2)锚节点在收到定位请求信息后，采集定位请求数据包的RSSI值，并向未知节点发送自身信息:节点ID、自身位置信息及RSSI值。

3)采用一定的距离估计方法，通过获得的各个RSSI值估计出未知节点到各个锚节点的距离测量值。

4)未知节点收到后建立锚节点集合Beacon_set={a1，a2，…，am}，本实验中m值为4。未知节点到锚节点的距离集合 Distance_set={d1，d2，…，dm}，锚节点位置集合 Position_set={(X1，Y1)，(X2，Y2)，…，(Xm，Ym)}。

5)已知切线y=x+bij与锚节点通信圆的切点:

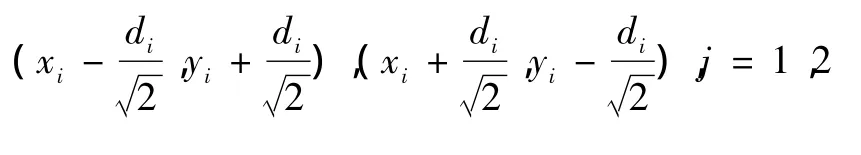
及切线y=－x+bij与锚节点通信圆的切点:

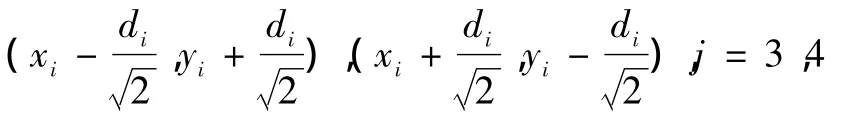
带入切线y=x+bij及y=－x+bij中，可以求得切线与y轴的截距:

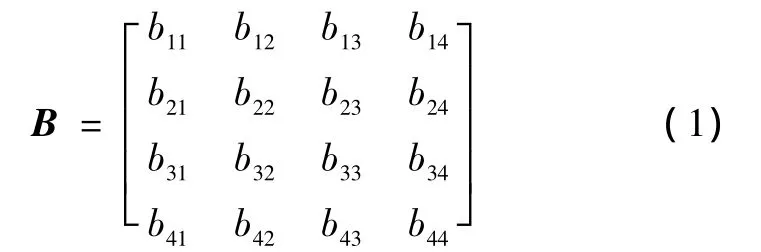
求 min(bi1)、max(bi2)、max(bi3)、min(bi4)可得圆外切线所组成的区域:

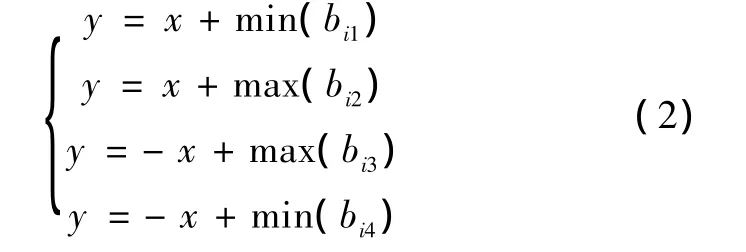
从图1可以看出，圆外切Bounding-box方法形成的搜索区域相对于其他Bounding-box方法所搜索的估计区域明显减小，因此能够大大提高定位的精度。该搜索区域的质心方程为

其坐标为

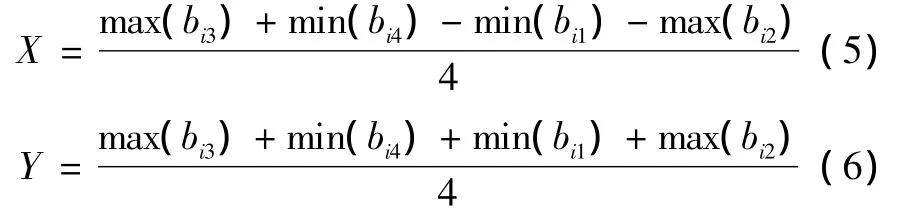
6)计算定位误差:设节点的真实坐标为(X，Y)，定位系统估计的坐标为()，使用均方根误差作为定位误差参数来评价定位的准确度［10］:

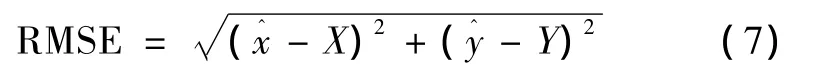
2 实验评估

首先对本文提出的圆外切Bounding-box及其他相关定位算法的性能进行评估和分析，分别采用仿真数据和实际定位环境中的RSSI值两类实验数据来评估定位方法的性能;然后对各定位算法的计算复杂度和能耗进行分析。

2.1 评估环境搭建

2.1.1 实验设置

1)仿真实验设置

定位环境为3.2 m×3.2 m的定位区域，在该区域的4个顶点布置了4个锚节点，未知节点则沿着2个坐标分别以0.8 m的间隔移动未知节点，如图2所示。共形成25个定位点。由于在4个顶点处未知节点与锚节点重合，因此将未知节点在x方向及y方向分别向正方形内部移动0.1 m。

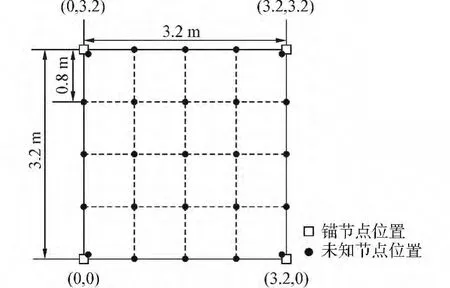
图2 定位区域示意图Fig.2 The localization field

2)实际WSN定位实验设置

节点是自研的CC2530模块，如图3所示。实验部署如图2所示，分别在室内走廊、大厅和室外开阔环境中的3.2 m×3.2 m范围内，进行定位试验，遇到未知节点与锚节点重合情况时，未知节点则在2个方向上各偏离0.1 m。

图3 节点实物Fig.3 The node used in experiments

2.1.2 评估数据集

为了全面评估所提出的定位方法，采用仿真数据和实际WSN定位数据2种评估数据集。

1)仿真数据集:向锚节点与未知节点间的距离值中加入N(0，σ2)噪声，σ分为2种情况讨论，分别为与距离d成正比的σ2=d/10，及与距离无关的σ2=0.2，为了计算在统计状态下的误差分布情况，在每个未知节点处计算150次均方根误差，并得到误差的平均值。

2)实际WSN定位数据集:在上述3种定位环境中，基于采集的实际RSSI数据(锚节点与未知节点间通信对应的RSSI值)，并采用基于RSSI数据的通信距离估计方法DEDC(distance estimation using data clustering)［4］得到距离估计值，然后对本文提出的圆外切Bounding-box定位方法的性能进行评估。

2.1.3 实验评估参数

均方根误差作为评估参数来评估定位方法的定位准确度，如式(7)所示，其值越小，则表示定位误差越小，定位的准确度越高。

2.1.4 实验设计

在实验评估时，首先应用圆外切Bounding-box定位方法对2种仿真数据进行定位，并和其他相关定位方法进行比较分析;然后基于实际WSN定位环境中的数据集对所提出方法进行评估，并和其他相关方法进行比较分析。最后对算法的计算时间复杂度、计算量、延迟和功耗进行分析和比较。

2.2 仿真数据评估

在仿真数据中，通过向锚节点与未知节点间的距离值中加入N(0，σ2)噪声引入距离估计误差，σ分为2种情况讨论，分别为与距离d成正比的σ2=d/10，及与距离无关的σ2=0.2，分别对这2种情况进行评估。

2.2.1 N(0，d/10)情况下定位误差分析

向锚节点与未知节点间的距离值中加入N(0，d/10)噪声，并应用 Bounding-box［2］(简写为 B-box)、三点 质 心 Bounding-box［3］、三 三 加 权 质 心 Boundingbox［3］、加权 Bounding-box［4］和圆外切 Bounding-box 5 种定位方法进行定位，并计算它们对应25个定位点的定位均方根误差，如图4所示。表1显示了定位算法的平均误差及最大误差情况。

图4 N(0，d/10)噪声时各方法的定位误差Fig.4 Localization error of different method with N(0，d/10)noise

由图4可知，相对于其他4种定位算法，圆外切改进Bounding-box定位算法在各定位点上对应的平均定位误差算法是最小的，说明圆外切改进Bounding-box算法具有较高的定位准确度。

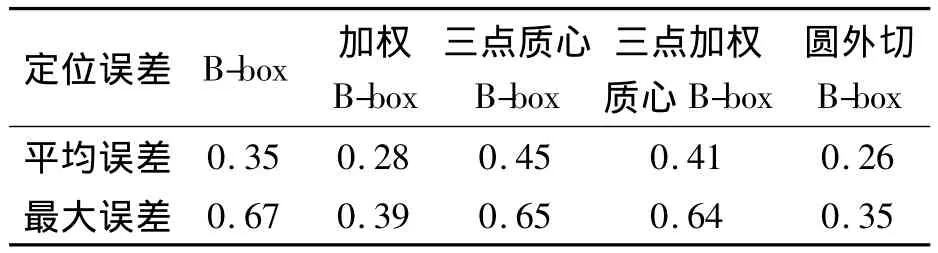
表1 N(0，d/10)的噪声时各方法的定位误差Table 1 Localization error of different methods with N(0，d/10)noise

由表1可见，相对于Bounding-box、加权Boundingbox、三点质心Bounding-box和三三加权质心Bounding-box定位算法，圆外切改进Bounding-box算法在平均误差上分别改善了 25.71%、7.14%、42.22%、36.59%，在最大误差上分别改善了47.76%、10.26%、46.15%和45.31%。

因此，相对于其他相关定位算法，圆外切改进的Bounding-box定位算法具有较高的定位准确度，这主要归因于其采用了与实际比较贴近的圆形的通信区域模型。

2.2.2 N(0，0.2)情况下定位误差分析

向锚节点与未知节点间的距离值中加入N(0，0.2)噪声，并应用 Bounding-box［2］(简写为 B-box)、三点 质 心 Bounding-box［3］、三 三 加 权 质 心 Boundingbox［3］、加权 Bounding-box［4］和圆外切 Bounding-box 5 种定位方法进行定位，并计算它们各自对应的25个定位点的定位均方根误差，如图5所示，表2显示了5种定位算法的平均误差及最大误差情况。

图5 N(0，0.2)噪声时各方法的定位误差Fig.5 Localization error of different method with N(0，0.2)noise

表2 N(0，0.2)的噪声时各方法的定位误差Table 2 Localization error of different methods with N(0，0.2)noise

由图5可知，相对于其他4种定位算法，圆外切改进B-box定位算法在各定位点上对应的平均定位误差算法是最小的。

由表2可见，相对于Bounding-box、加权Boundingbox、三点质心Bounding-box和三三加权质心Boundingbox定位算法，圆外切改进Bounding-box算法在平均定位误差上分别改善了 35.29%、4.35%、50.00%、43.59%，在最大误差上分别改善了 50.00%、0.00%、49.21%和49.21%。

综上，2种噪声情况下的实验结果表明，本文提出的圆外切Bounding-box改进定位算法具有较高的定位准确度，同时加权的Bounding-box方法也具有较高的定位准确度。

2.3 实际WSN定位评估

在上述3种典型定位环境中，对25个定位点的RSSI数据进行采集，并采用DEDC［4］方法进行距离估计，并将得到距离估计值应用到 Bounding-box［2］、加权Bounding-box［4］、三三质心 Bounding-box［3］、三三加权质心Bounding-box［3］和本文提出的圆外切 Bounding-box定位方法中，并比较它们的定位均方根误差。3种典型定位环境中，各定位方法对应的定位误差如表3、表4和表5所示。表中的改善程度是圆外切Bounding-box改进算法相对于其他算法的定位误差降低的百分比。

表3 走廊环境中25个定位点的平均定位误差Table 3 Mean of localization error of 25 points in corridor

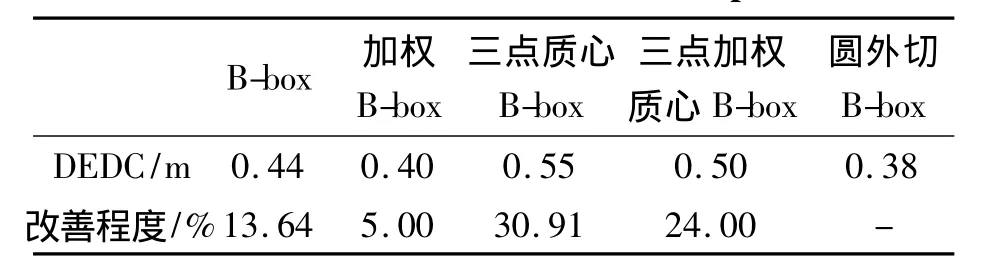
表4 大厅环境中25个定位点的平均定位误差Table 4 Mean of localization error of 25 points in hall

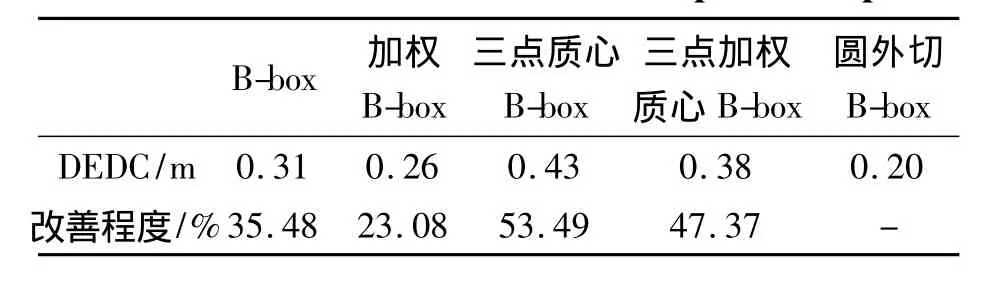
表5 室外环境中25个定位点的平均定位误差Table 5 Mean of localization error of 25 points in open air

2.3.1 定位方法比较分析

由表3、4和5可以看出，圆外切B-box定位算法具有较低的定位误差:

在室内走廊环境中，相对于其他算法，圆外切Bounding-box定位算法分别将定位误差平均改善了1.59% 、8.82% 、11.43% 和 7.46% 。

在室内大厅环境中，相对于上述其他定位方法，圆外切Bounding-box定位算法分别将定位误差平均改善了 13.64% 、5.00% 、30.91% 和 24.00% 。

在室外开阔环境中，相对于上述其它定位方法，圆外切Bounding-box定位算法分别将定位误差平均改善了 35.48% 、23.08% 、53.49% 和 47.37% 。

综上，圆外切Bounding-box定位算法具有较低的定位误差。特别是室外环境中具有很明显的优势，这主要是因为其考虑了无线传感器节点的通信区域模型，并通过切线组成的区域来减小估计范围，获得较高精度的定位结果。同时加权Bounding-box方法也具有较好的定位结果。

2.3.2 定位环境比较分析

由表3、4和5可知，在室内走廊环境中，所有算法的定位误差都很大，室内大厅环境中次之，而室外开阔环境中最小。因为室内走廊通信环境复杂，使得RSSI值的不确定性较大，导致定位误差较大。而在室外开阔环境中，不确定性因素较少存在，使得定位误差较小。因此在部署定位系统时，应考虑环境因素对系统定位准确度的影响。

2.4 计算复杂度和能耗分析

对算法的计算复杂度、延时和能耗进行分析。

2.4.1 计算复杂度分析

对 Bounding-box［2］、加权 Bounding-box［3］、三 三 质心 Bounding-box［3］、三三加权质心 Bounding-box［4］和本文提出的圆外切Bounding-box定位方法的计算时间复杂度分析如表6所示。其中，m为锚节点个数，n为要定位点的个数。从表6可以看出，上述几种定位方法的计算复杂度是相同的。而在具体计算量上有所差异，对上述几种方法的计算量进行分析，如表7所示。

表6 定位方法计算复杂度分析Table 6 Calculation complexity analysis of different ocalization methods

表7 定位方法的计算量分析Table 7 Calculation analysis of different localization methods

从表7可以看出，所有Bounding-box改进算法相对于其基本方法，计算量均有所增加。其中圆外切Bounding-box方法的计算量高于Bounding-box方法及加权Bounding-box方法。因此，可以看出，定位精度的提高是以增加计算量为代价的。同时基于质心的方法计算量是最大的。因此，要根据具体的应用需求，来选择合适的定位方法。

2.4.2 延时分析

本文中无线传感器节点的微控制单元是基于8位的SOC架构，可运行频率在32 MHz［11］。假定采用单指令周期处理方式。执行加/减运算为1个指令周期，执行比较运算为2个指令周期，执行乘/除法运算为5个指令周期，则结合表7中的计算量分析，可得上述几种定位方法的时延如表8所示。

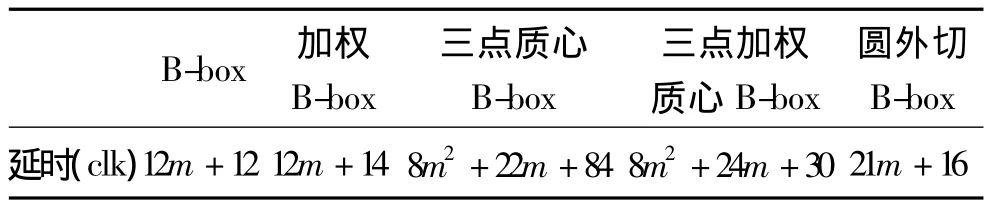
表8 定位方法的时延分析Table 8 Latency analysis of different localization methods

从表8可以看出，B-box、加权B-box和圆外切B-box定位方法的延时在一个数量级，且明显低于基于质心的B－box定位方法。因此综合考虑定位性能和时延，圆外切B-box定位算法具有明显的优势。

2.4.3 能耗分析

由于能量主要耗费在节点间的无线通信上［12］，根据文献［12］中传感器节点能量消耗模型，可得

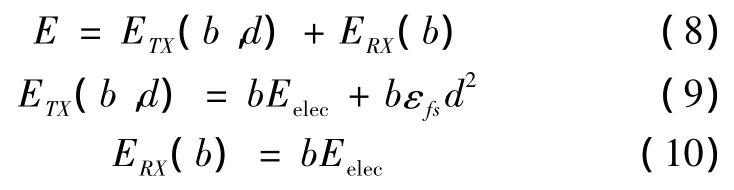
式中:ETX(b，d)为向距离为d的节点发送b比特数据消耗的能量;ERX(b)为接收b比特数据消耗的能量;Eelec为接收b比特数据消耗的能量，典型值为50 nJ/bit;εfs为功率放大所需的能量，典型值为10 pJ/bit/m2。

上述各方法的定位过程是相同的。均是未知节点广播定位请求数据包，各个锚节点收到该包后，发送响应数据包，返回自己的ID、位置信息以及接收到数据包的RSSI值。假定定位请求数据包长度为136 bit，响应数据包长度为178 bit。则采用m个锚节点进行定位时，整个定位系统消耗的能量为

由式(11)可知，主要的能量消耗在无线通信上。不同定位方法的计算量有所不同，但对于无线通信而言，可以忽略。因此，应尽量减小无线通信的次数以及通信时的数据长度。

3 结束语

目前Bounding-box及其改进定位算法普遍采用正方形作为WSN节点通信范围模型，与实际的模型不一致，导致较大的WSN定位误差。针对该问题，本文提出了圆外切Bounding-box改进定位算法。综合考虑定位精度、计算复杂度、计算量、时延和能耗等因素可知:圆外切Bounding-box定位方法是以提高一定计算量为代价换取定位精度的提高，为WSN定位应用系统提供了一种技术方案选择。因此，需要根据具体的需求，选择合适的定位方法。定位方法的优化选择也是下一步研究的主要内容。

［1］EUNCHAN K，KISEON K.Distance estimation with weighted lease squares for mobile beacon-based localization in wireless sensor networks［J］.IEEE Signal Processing Letters，2010，17(6):559-562.

［2］詹杰，刘宏立，刘述钢，等.基于RSSI的动态权重定位算法研究［J］.电子学报，2011，39(1):82-87.ZHAN Jie，LIU Hongli，LIU Shuxinag，et al.The study of dynamic degree weighted centriod localization algorithm based on RSSI［J］.Acta Electronica Sinica，2011，39(1):82-87.

［3］郭海琦.基于ZigBee的无线传感器网络定位算法的研究与应用［D］.成都:西南交通大学，2007:19-32.GUO Haiqi.Research of the localization method based on ZigBee［D］.Chengdu:Southwest Communication University，2007:19-32.

［4］王丹.基于RSSI的无线传感器网络定位研究［D］.哈尔滨:哈尔滨工业大学，2011:44-48.WANG Dan.Research on the localization method based on RSSI for wireless sensor network［D］.Harbin:Harbin Institute of Technology，2011:44-48.

［5］姚英彪，曾嵘，易志强.基于边框定界的WSN分布式全搜索定位算法［J］.通信学报，2012，33(Z2):135-140.YAO Yingbiao，ZENG Rong，YI Zhiqiang.Bounding box based distributed search localization algorithm for WSN［J］.Journal of Communications，2012，33(Z2):135-140.

［6］SANABRIA-RUSSO L，CANO C，BELLALTA B.Localization procedure for randomly deployed WSNs based on the composability of position estimation protocols［C］//Proceedings of 9thInternational Wireless Communications and Mobile Computing Conference.Sardinia，Italy，2013:621-626.

［7］SHI Xin，ZHANG Linghua.High-precision weighted Bounding Box localization algorithm for wireless sensor network［C］//Proceedings of 2013 IEEE 3rd International Conference on Information Science and Technology(ICIST 2013).Yangzhou，China，2013:1110-1113.

［8］YANG Yuan，ZHAO Yubin，KYAS M.Weighted least-squares by bounding-box(B-WLS)for NLOS mitigation of indoor localization［C］//Proceedings of IEEE Vehicular Technology Conference.Yangzhou，China，2013:1110-1113.

［9］程伟，史浩山，王庆文.基于差分修正的传感器网络加权质心定位算法［J］.系统仿真学报，2012，24(2):389-393.CHENG Wei，SHI Haoshan，WANG Qingwen.Weighted centroid localization algorithm based on different correlation for sensor network ［J］.Journal of System Simulation，2012，24(2):389-393.

［10］LUO Qinghua，YAN Xiaozhen，LI Junbao，et al.DDEUDSC:dynamic distance estimation using uncertain data stream clustering in mobile wireless sensor networks［J］.Measurement，2014，55:423-433

［11］LUO Qinghua，PENG Yu，PENG Xiyuan，et al.Uncertain data clustering-based distance estimation in wireless sensor networks［J］.Sensors，2014，14(4):6584-6605.

［12］HEINZELMAN W B，CHANDRAKASAN A P，BALAKRISHNAN H.An application-specific protocol architecture for wireless microsensor networks［J］.IEEE Transactions on Wireless Communications，2002，1(4):660-670.