非参数季节分解模型太湖叶绿素a浓度变化特征研究

张以飞，汪　靓，王玉琳

(1.南京大学环境规划设计研究院有限公司，南京　210046；2.河海大学环境学院， 南京　210098)

· 试验研究 ·

非参数季节分解模型太湖叶绿素a浓度变化特征研究

张以飞1，汪靓2，王玉琳2

(1.南京大学环境规划设计研究院有限公司，南京210046；2.河海大学环境学院， 南京210098)

在湖泊各种水质指标中，叶绿素a是表征营养状况最重要的指标之一。使用基于季节分解技术的局部线性回归的非参数方法研究了梁溪河口、梅梁湾和湖中心3个太湖不同区域1995年～2006年期间叶绿素a观测值变化特征。结果表明该方法能有效的分开太湖叶绿素a观测值时间序列中的趋势成分和季节效应成分。趋势成分结果表明，太湖的叶绿素a浓度在1997年中达到顶峰；1998年～2001年期间3个区域的叶绿素a浓度趋势一直下降，随后各有不同；3个区域叶绿素a浓度变化趋势在2001年之前保持良好的响应关系，此后梁溪河口叶绿素a浓度对梅梁湾和太湖中心的影响减弱。季节成分表明3个区域叶绿素a的年最高值都出现在8月份，但5月～6月的浓度很可能比7月份更高；冬春季节3个区域的叶绿素a浓度保持良好的响应关系，而夏季彼此的响应减弱。季节成分模式在1998年和2003年分别出现一个结构变化：前者使太湖每年秋末到春末的叶绿素a浓度下降，但是夏秋两季的浓度升高；后者使叶绿素a浓度的季节效应变的平稳。这些结果为太湖污染控制提供了理论依据。

叶绿素a；局部线性回归；季节分解； 趋势成分；季节效应

当前我国湖泊水环境的保护和改善已受到各级政府和湖泊周围地区居民的高度关注。在影响湖泊水体水质的各种污染物中，叶绿素a作为水生植物含有的主要色素之一，是表征水体营养状况的重要指标，通过叶绿素a的情况能了解水体生态系统的情况及其富营养化的水平[1～3]，因此研究湖泊的叶绿素a的随时间变化的规律对掌握湖泊富营养化特征的变化有着十分重要的作用。

前人学者已进行了大量叶绿素a与其它环境因素之间的关系研究，Joseph A Krewer等[4]用线性回归和曲线回归方法研究了水体中溶解态磷与叶绿素a的关系；Bobbin J等[5]用遗传算法研究了叶绿素a的变化规律，并用于预测藻类暴发；陈宇炜等[6]用逐步多元回归和相关分析法研究了梅梁湾叶绿素a与营养盐之间的关系；白晓华，胡维平[7]用一元回归法研究了太湖水深变化对营养盐和叶绿素a的影响；李未等[8]用小波分析研究了太湖营养化的主要驱动因子等。

各国学者对叶绿素a与环境要素关系研究比较充分，但是对湖泊中叶绿素a本身中长期变化规律的研究很少，龚绍琦等[9]使用参数统计方法，建立了太湖不同区域叶绿素a时间序列的 ARMA模型；他们认为太湖中营养区、轻富营养区和中富营养区分别符合不同参数的AR(1)、MA(5)以及AR(6)模型，这一结果是有意义的，但是，这一参数统计方法要求数据本身符合正态性假设[10]，这一点在实际的观测数据中并不容易得到满足。同时由于叶绿素a本身变化受气候等自然节律和因素影响极大，因此肯定具有季节性规律；而之前建立的ARMA等模型显然并没有考虑季节性因素的影响，所以是不适当的；季节性规律与长期趋势混杂在一起，也将使数据规律分析产生困难，掩盖真实的情况，所以也应分开考虑。

另一方面，太湖及周边区域在我国社会经济发展中占有很重要的地位，而且从上个世纪90年代中期至本世纪最初的10年间，恰恰是太湖蓝藻爆发最频繁的时期；研究这一时间段内太湖叶绿素a浓度的变化规律不但对治理太湖有重要的理论和实际意义，也对控制其它区域的富营养化问题有着借鉴意义。因此，本文利用非参数统计思想，采用季节分解的局部线性回归模型研究1995年～2006年期间太湖的叶绿素a浓度的变化规律；这一方法不但对数据要求较低，更吻合实测数据的要求；更重要的是它能将季节性规律和长期趋势分开，从而清楚的展现叶绿素a时间序列的变化趋势，揭示太湖叶绿素a的季节性规律和长期趋势，为太湖污染控制提供了理论依据。

1　理论模型

局部线性回归是一种新的非参数时间序列方法；该方法可以比较好的区分时间序列中的趋势成分和季节成分[11,12]，不但适用于平稳时间序列，也可以适用于非平稳时间序列。

1.1局部线性回归

一般地，叶绿素a浓度的时间序列{Yt,t}能够分解成下式：

Yt=ft+st+εt

(1)

式中ft表示慢变函数，表示时间序列的趋势成分；st是周期函数，表示时间序列的季节效应成分；εt为残差。在局部线性回归中，趋势项ft由下式估计：

(2)

其中h称为趋势窗口宽度，用于控制局部回归作用的范围，h越大表示局部线性回归作用的范围越大。局部线性回归中用到的窗口宽度是可调的，没有一定的选择规则；而且局部线性回归的结果，对h并不敏感[12]；对于一个具体的时间序列，可以根据叶绿素a浓度的生态学特点来初步选择，并通过检验结果残差是否满足正态性判断h选择的正确性[11]。i为一确定的时间；而t为观测值Yt对应的时间。在(2)式中，由于是局部线性回归，所以a, b不能由最小二乘法(Ordinary Least Square, OLS)得到；而是通过下式获得：

(3)

其中Kh(t)为核函数，它在此的作用即是权，使得距离t点越远其影响越小。通常使用的核函数为：

(4)

上述局部线性回归方法在具有季节效应的时间序列中需要进行修正。季节效应修正主要的思想是首先通过一个低通量过滤器估计叶绿素a观测值的季节性部分，然后用观测值减去季节性部分的残差估计趋势部分，并如此反复迭代；即每个部分都根据其它部分的残差来拟合。当前后两次迭代得到结果差别不大时，认为完成估计；迭代的初始值可以设置为零。

为了减少异常值对结果的影响，在每一次迭代循环中对核函数加权，权函数取为下式：

(5)

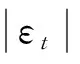
(6)

权函数的作用是减少迭代中残差特别大的观测值的权重，从而减少异常点的影响。此外，如果一个观测值的计算权重小于限定值可以认为是异常点；能够进行异常点识别也是局部线性回归季节分解模型的一个优点；在本文中计算权重小于10-8被识别为异常点。

2　数据来源与处理

本文的观测数据来源于江苏太湖湖泊生态系统国家野外科学观测研究站(简称“太湖站”)[13]，该文献有全太湖32个野外站点中8个站点的自1991年～2006年共16年的逐月观测数据。选择位于无锡梁溪河河口的0号基准站，位于梅梁湾的4号基准站以及太湖中心的8号基准站进行研究，以反映太湖不同区域的叶绿素a时间序列的特点。这些观测站1995年～2006年每个站点有144个数据，共576个数据，观测数据比较完整，有比较大的研究价值。

3　模型分析与计算

在进行具体分析之前，先了解太湖叶绿素a浓度变化的概况。表1是对3个站点叶绿素a的观测值初步统计分析的结果。结果表明，无论是最大值，中位数，平均值8号点叶绿素a的情况都是其中水质是最好的，其它站点的数据大致上离太湖中心越近的站点，其情况越好，这一点与之前研究相符[14,15]；从标准差来看，8号站点的标准差也最小，表明8号点叶绿素a年际情况相对比较稳定；其它3个站点的观测值年际则表现出较大的起伏。所有站点观测值的偏度都大于0，尤以8号站点最为明显，这说明这些站点的叶绿素a观测值的分布右偏，也就是说8号点叶绿素a更容易出现极端高值。从峰度和偏度来看，3个站点的叶绿素a值的分布都明显的偏离正态分布，因此使用普通的回归分析等统计方法是不合适的。

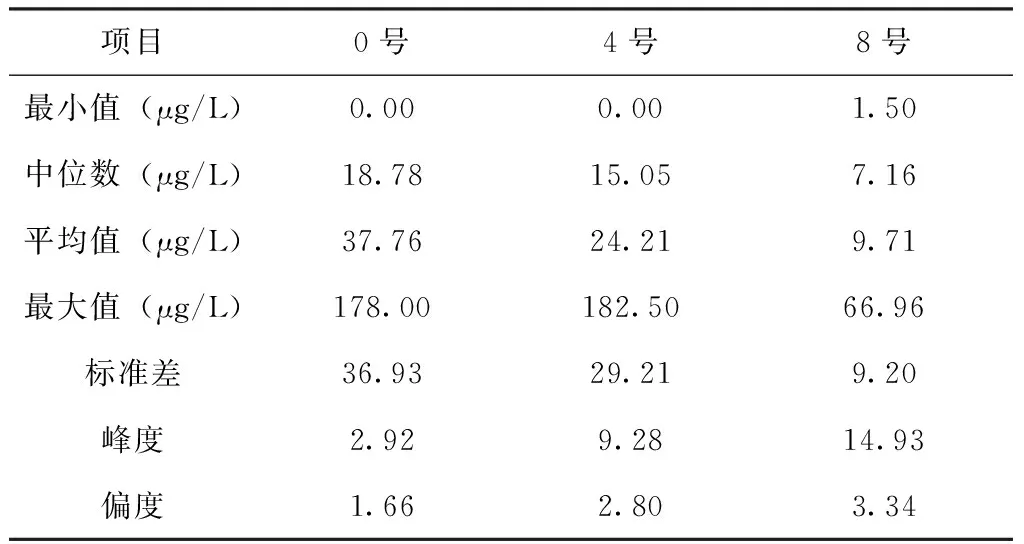
表1　叶绿素a统计量表

图1是3个站点1～20阶的自相关系数图。从中可以看出，0号点的叶绿素a观测值相关系数随着滞后期的增大减小的很慢，这与龚绍琦等[9]人的研究结果类似；这些现象应该是由于该点位于河口，其受人类生产生活等有规律的活动的调控影响较大，叶绿素a浓度延续性比较大，从而前后月观测值表现出比较强的关联性。4号点叶绿素a的相关系数衰减较慢，但是变化并不规律，这是因为其位置在梅梁湾近岸，它的观测值不但受到人类活动的较大影响；而且周围地形、水力条件等自然条件非常复杂。8号点的自相关系数则衰减较快，表明太湖湖心叶绿素a的浓度和其前后月的观测值基本没有关系。

3个站点的叶绿素a观测值在滞后期为12处的相关系数都比较大，超过了95%置信区间，这表明了其中存在明显的季节效应，时间序列模型需要考虑这一因素的影响；以前的学者建立的ARMA模型并没有考虑这一点，因此并不适当。从自相关系数可以看出太湖不同区域的叶绿素a的时间变化规律明显不同，人类活动增大了近岸区叶绿素a的时间自相关；更重要的是太湖叶绿素a浓度存在明显的季节效应，不考虑季节效应对于研究太湖叶绿素a的变化规律是不合适的。

图1　叶绿素a浓度自相关系数Fig.1　The ACF of chl-a concentrations

根据以上分析的结果，3个站点的叶绿素a观测值的局部线性回归模型窗口宽度都选为12。图2是模型残差的正态分位数图。可以看到，0号点和8号点的残差都很好的满足正态分布的要求；4号点的残差虽然在边界处略有偏差；但这主要是边界效应的体现，对结果影响不大，可以认为模型是符合统计学要求的[12]。

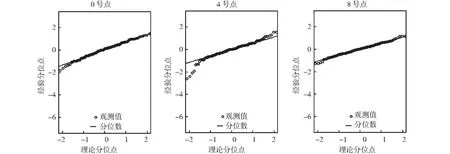
图2　模型残差分位数Fig.2　The Q-Q plot of models residuals

表2给出了3个站点拟合误差情况。比较而言，可以发现位于太湖中心的8号点由于所处环境简单，受人类影响较小，规律比较清晰，模型效果明显好于其它两个站点的情况。相对来说，4号点的模型误差较大，是因为梅梁湾水力、地形条件都比较复杂；藻类生长受到的不确定因素较多。

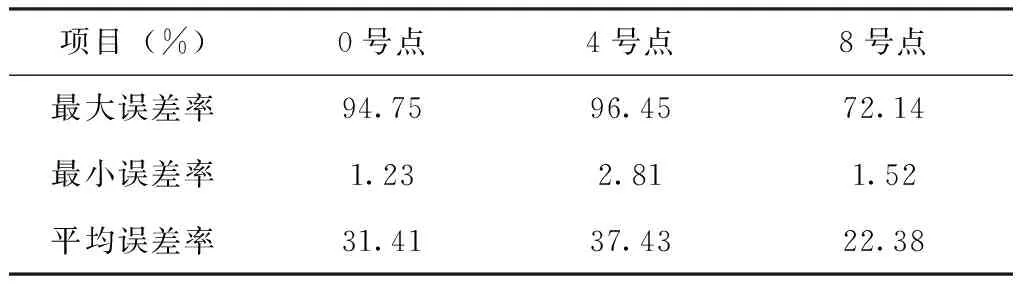
表2　模型误差

图3表明了3个站点的对数叶绿素a观测值的拟合情况。可以看出，拟合值与观测值在大多数情况下是非常吻合的；误差比较大的区域出现在时间边界上，这主要是因为在边界上可被利用的观测值比较少；此外，虽然0号点和4号点分别有5个异常点，8号点有两个异常点，但是所有的拟合曲线几乎没有受到异常点的影响，这表现出局部线性回归对异常点良好的稳健性。需要注意的是，在图3中，由于季节规律和趋势效应相混杂，叶绿素a的变化规律是不明显的。

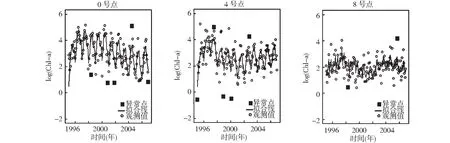
图3　模型拟合图Fig.3　The fits of the models

4　结果与讨论

4.1趋势效应

图4是3个站点叶绿素a浓度的趋势分析图；可以看到经过季节分解后，3个站点的叶绿素a浓度变化趋势显得清晰很多。在1997年之前，3个站点的叶绿素a都在不断的上升，并在1997年～1998年期间先后达到顶峰，随后有所下降。这主要是因为太湖在“九五”被定为水污染防治重点，而《太湖水污染防治“九五”计划及2010年规划》则是在1998年1月得到国务院批复的[16,17]；这一结果与当时的太湖治理背景是相符的。需要注意的是最先达到顶峰的是0号点的叶绿素a浓度，其次是4号点的叶绿素a浓度，最后是8号点的浓度彼此间隔有2～3个月；并考虑到0号点监测的梁溪河口在当时是太湖的主要污染源之一，可以认为这3个站点的叶绿素a浓度下降有一定的因果关系；即这一时期梁溪河污染的削减，显著降低了梅梁湾的叶绿素a浓度，也减小了太湖中心区域叶绿素a的浓度。

从1998年～2001年期间，梁溪河口、梅梁湾和太湖中心叶绿素a浓度均有所下降；从曲线上看，此时梅梁湾叶绿素a浓度与梁溪河口浓度仍然保持一定的响应关系。2001年以后3个区域的叶绿素a浓度变化趋势出现显著差异：2001年～2004年期间梅梁湾和太湖中心的叶绿素a浓度呈现出上升趋势；梁溪河口叶绿素a的浓度则继续呈现出比较快的下降趋势；2004年以后梁溪河口的叶绿素a浓度经过一番波动以后，出现一定的上升趋势；太湖中心的叶绿素a浓度则呈现下降趋势，这些与顾苏莉等人的研究结果相同[18]。3个区域叶绿素a浓度的差别表明，2001年以后随着治理工程的展开和叶绿素a浓度的降低，太湖中心叶、梅梁湾和梁溪河口叶绿素a浓度彼此的响应关系逐步减弱。由于梅梁湾以及整个太湖周围农业发达，且观测数据表明1998年～2004年期间太湖的水温，水深，光照强度等气候与水文因素相较于其前后年均无明显变化[13]，因此分析它们的叶绿素a浓度响应关系减弱的主要原因是梁溪河的点源污染受到控制以后，比较难控制农业面源污染以及太湖底泥中释放的内源污染开始占主导地位。

从单纯的趋势成分来看，2006年底3个站点叶绿素a浓度与1995年初3个站点叶绿素a的浓度相差无几；但是，相较于其1997年它们最高的时叶绿素a浓度的对数值分别下降了33.9%，27.4%和35.1%。特别要指出，由于2005年以后梁溪河口叶绿素a的趋势成分已经低于同期梅梁湾叶绿素a的趋势成分，显示单纯控制梁溪河污染，对降低梅梁湾叶绿素a浓度已经不会有太大的意义。

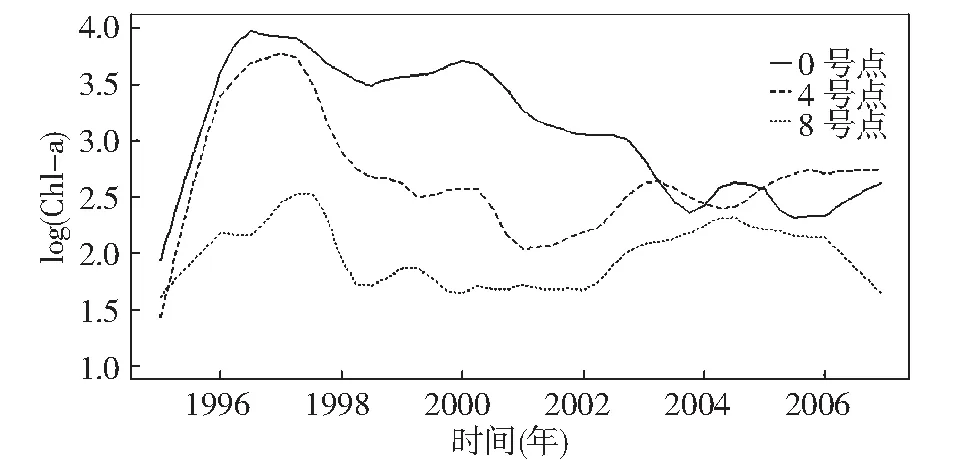
图4　 叶绿素a趋势成分Fig.4　The trend components of chl-a

4.2季节效应

图5表现了3个站点叶绿素a的季节效应成分。可以看到，3个站点的叶绿素a季节效应有着一些相同的特点：每年的1月份是叶绿素a最低的时候，从春季开始随着气温的上升叶绿素a浓度逐渐上升并于8月份达到一年的最高值。但是季节效应曲线表明与其临近的月份做比较，梁溪河、梅梁湾与太湖中心的7月份叶绿素a的情况并不特别高；反而是5月和6月的叶绿素a浓度比7月份浓度高。

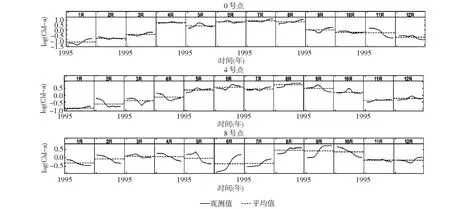
图5　叶绿素a季节成分Fig.5　The seasonal components of chl-a

此外，3个区域的叶绿素a浓度季节变化也显示出一些不同的特点：梁溪河口与梅梁湾的叶绿素a在每年的1月～7月期间基本一直在上升，在8月份达到顶峰后开始下降，在次年的1月份达到最低值；太湖中心的叶绿素a在每年的春季4月份达到一个高峰以后，在5月～7月有所下降。需要注意，梁溪河口叶绿素a浓度在4月突然上升，而梅梁湾的叶绿素a浓度则在5月突然上升，可以认为这两者之间有一定的响应关系。另一方面，虽然太湖中心8月份的叶绿素a也突然上升，但是上升幅度大于梅梁湾的幅度，且时间相隔较长，这表明太湖中心每年的8月的叶绿素a浓度与梅梁湾和梁溪河口的叶绿素a 浓度关系相对较小，应该有自身的天然因素起作用。总之，从季节因素来看，梅梁湾叶绿素a的季节成分与梁溪河口的季节成分有一定的响应关系；而梅梁湾夏季的叶绿素a季节成分与太湖中心夏季季节成分响应关系比较弱。

从细节来看，几乎所有的季节效应曲线都表在1998年左右显示出一个结构变化；1998年之后，每年11月～12月以及1月～4月叶绿素a浓度大多呈下降趋势，但是5月～9月叶绿素a浓度有所上升；这表明太湖污染控制工程对冬春两季叶绿素a控制表现出良好的效果，而对夏秋两季叶绿素a浓度的控制效果不明显。

2003年左右叶绿素a的季节效应也表现出一个轻微的改变，这一点在每年的5月～9月的季节曲线上表现的尤其明显；2003年后叶绿素a全年的季节效应曲线都比较平稳，变化很小。

5　结　论

本文对太湖叶绿素a浓度的时间序列进行分析，结果发现太湖不同区域叶绿素a浓度的自相关性区别较大，越靠近湖岸自相关系数衰减越慢；近岸区自相关性比较强，而湖心区自相关性较弱；但是3个区域叶绿素a的浓度分布都较大的偏离了正态分布；同时，分析表明太湖叶绿素a浓度值有强烈的季节性规律。具体来说：

5.1本文所使用基于非参数季节分解局部线性回归方法则能够很好的将太湖叶绿素a浓度观测值的趋势成分与季节成分分开，更清晰的表达了太湖不同区域叶绿素a的长期趋势和季节模式。

5.2从趋势成分来看，3个区域太湖叶绿素a浓度在1997年中达到顶峰；2001年前梅梁湾和太湖中心叶绿素a浓度趋势与梁溪河口叶绿素a的浓度趋势有明显的响应关系；2001年后梁溪河口叶绿素a情况对梅梁湾和太湖中心的影响逐步减弱。

5.3从季节效应来看，3个区域叶绿素a浓度最高点都出现在每年的8月份；梁溪河口与梅梁湾的叶绿素a浓度有较强的响应关系；但太湖中心区域夏季的叶绿素a的浓度的突然上升过程与梅梁湾叶绿素a变化的关系不大。

[1]Office of water. Ambient water quality criteria recommendations: Information supporting the development of state and Tribal nutrient criteria, lakes and reservoirs in nutrient ecoregion II (EPA-822-B -00-007) [R]. Washington,D.C:United States Environmental Protection Angency,2000.1-30.

[2]张运林，秦伯强，陈伟民,等.太湖梅梁湾浮游植物叶绿素a和初级生产力[J].应用生态学报，2004,15(11):2127-2131.

[3]Kalff J.Limnology[M].London: Prentice Hall,2001.

[4]Krewer J A,Holm H W. The phosphorus-chlorophyll a relationship in periphytic communities in a controlled ecosystem [J]. Hydrobiologia, 1982,(94):173-176.

[5]Bobbin J,Recknagel F. Inducing explanatory rules for the prediction of algal blooms by genetic algorithms [J]. Environmental International,2001,(27):237-242.

[6]陈宇炜，秦伯强，高锡云. 太湖梅梁湾藻类及相关环境因子逐步回归统计和蓝藻水华的初步预测[J].湖泊科学,2001,13(1):63-71.

[7]白晓华，胡维平. 太湖水深变化对氮磷浓度和叶绿素a浓度的影响[J].水科学进展,2006,17(5):727-732.

[8]李未，秦伯强. 太湖梅梁湾富营养化主要驱动因子的多时间尺度分析[J].湖泊科学,2012,24(6):865-874.

[9]龚绍琦，黄家柱，李云梅,等. 应用时间序列分析法对太湖叶绿素-a含量的动态研究[J].海洋与湖沼,2008,39(6):591-598.

[10]王星.非参数统计[M].北京：清华大学出版社,Springer,2009.

[11]Song S Q.环境与生态统计—R语言的应用[M].北京：高等教育出版社，2011.

[12]Cleveland R B,Cleveland W S,McRae J E,et al. STL: A Seasonal-Trend Decomposition Procedure Based on Loess [J]. Journal of Official Statistics, 1990,(6):3-33.

[13]秦伯强，胡春华.中国生态系统定位观测与研究数据集—湖泊湿地海湾生态系统卷，江苏太湖站(1991-2006)[M].北京：中国农业出版社，2010. 239-270.

[14]旷达，韩秀珍，刘翔,等.基于环境一号卫星的太湖叶绿素a浓度提取[J].中国环境科学,2010,30(9):1268-1273.

[15]张玉超，钱新，钱瑜,等.支持向量机在太湖叶绿素a非线性犯严重的应用[J].中国环境科学,2009,(1):78-83.

[16]刘鸿志，陈永请，梁占彬.我国重点湖泊的水环境管理(一)[J].环境保护，1998,(12):9-10.

[17]顾岗.太湖蓝藻暴发原因及其控制措施[J].上海环境科学，1996，15(12):10-14.

[18]顾苏莉，陈方，孙将陵.太湖蓝藻监测及暴发情况分析[J].水资源保护,2011,27(3):28-32.

Research on Concentration Variation Characteristics of Chlorophyll a in Taihu Lake Based on Nonparametric Seasonal-Trend Decomposition Model

ZHANG Yi-fei1, WANG Liang2，WANG Yu-ling2

(1.InstituteofEnvironmentalPlanning&DesignNanjingUniversity,Nanjing210046,China;2.CollegeofEnvironment,HohaiUniversity,Nanjing210098,China)

Chlorophyll a (Chl-a) is one of the most important nutrient factors of the lake. The nonparametric method of local linear regression based on seasonal-trend decomposition procedure has been used to study the variation characteristics of observed values of Chl-a during 1995 to 2006 years. The studied areas were mouth of Liangxi River, Meiliang Bay and the center of the lake. The results indicated that the method could effectively decompose the seasonal and the trend components in the observed time series of Chl-a. The trend component showed the Chl-a concentration peaked at 1997, and during 1998 and 2001, the concentrations of Chl-a had been declining first and then different in the three regions. The concentration change trend of Chl-a in studied regions presented good response relationship before 2001, and after then the impact of Chl-a concentration in Liangxi river mouth on the Meiliang Bay and the center of Taihu Lake had reduced. The seasonal component showed that the peak concentration of Chl-a in the three regions appear in August. However, the concentrations in May and June would be higher than that in July. The response relationship among the regions held well in spring and winter but diminished in summer. In 1998 and 2003, respectively, there was a structure variation point for the seasonal components. The first one made the concentrations of Chl-a in Taihu Lake decrease from late autumn to late spring, but increase in summer and autumn. The second one made the seasonal components stable. The research could provide theoretical basis for pollution control of Taihu Lake.

Chlorophyll a; local linear regression; seasonal decomposition; trend component; seasonal influence.

2014-09-26

张以飞(1982-),男，江苏泗阳人，2004年毕业于河海大学环境工程专业，工程师。研究方向为环境规划，水环境保护。

X524

A

1001-3644(2015)02-0026-07