不等式的几种证明方法*

鲁翠仙

（临沧师范高等专科学校数理系，云南 临沧 677099）

不等式的几种证明方法*

鲁翠仙

（临沧师范高等专科学校数理系，云南 临沧 677099）

利用分块矩阵和初等变换的性质给出了3种证明不等式的方法，并得到了不等式的本质及其等号成立的充要条件。

不等式；证明；初等变换；分块矩阵

1 预备知识

2 证明方法

根据分块矩阵的初等行（列）变换不改变矩阵的秩，以及结论2，得

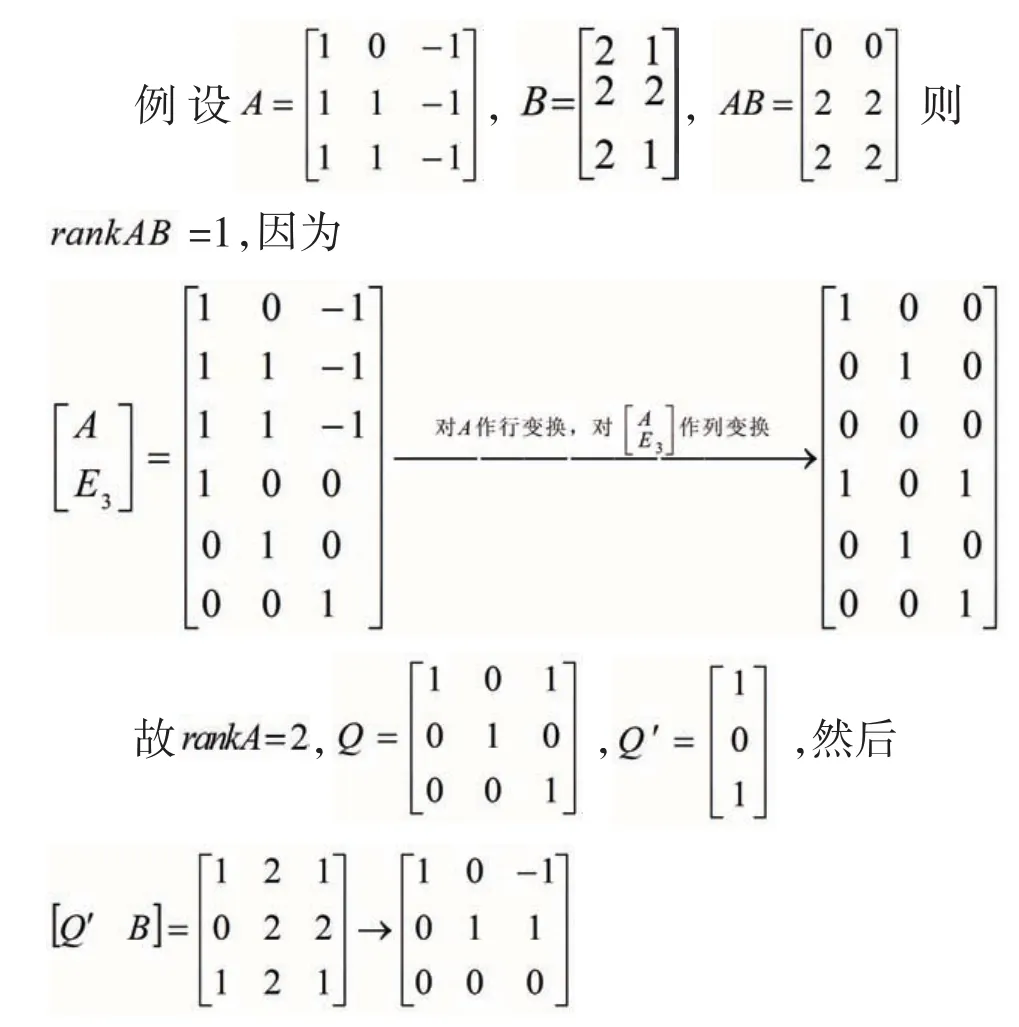
注释及参考文献：

[1]丘维声.高等代数(第二版)[M].北京:高等教育出版社,2001.

[2]北京大学数学系.高等代数[M].北京:高等教育出版社,1988.

[3]张枚.高等代数习题选编[M].杭州:浙江科学技术出版社,1985.

[4]黄卫红,杨兴东,周月军.矩阵Sylvester不等式与Frobenius不等式等号成立的条件[J].南京气象学院学报,2007,30(2):279-283.

Several Methods to the Evidence of Sylvester Inequality

LU Cui-xian
（Department of Mathematical，Lincang Teachers College，Lincang，Yunnan 677099）

In this paper,by using the properties of elementary transformation and partitioned matrices we give three method to prove Sylvester inequality and we explore the nature of the Sylvester inequality and the necessary and sufficient conditions when equals established.

Sylvester inequality；proof；elementary transformation;partitioned matrices

O178

A

1673-1891（2015）02-0026-02

2015-04-02

2013年临沧师范高等专科学校科研课题（项目编号：LCSZL2013008）。

鲁翠仙（1980-），女，彝族，云南凤庆人，副教授，硕士，主要从事代数、计算方法方面的研究。