含参不等式恒成立问题

刘海霞

判别式法

若所求问题可转化为二次不等式，则可联想到二次函数图象结合判别式解题.一般地，对于二次函数[f（x）=ax2+bx+c（a≠0，x∈R）]，则有：（1）[f（x）>0]对[x∈R]恒成立[?a>0，Δ<0；]（2）[f（x）<0]对[x∈R]恒成立[?a<0，Δ<0.]

例1 已知函数[y=lg[x2+（a-1）x+a2]]的定义域为[R]，求实数[a]的取值范围.

解析 由题设可将问题转化为[x2+（a-1）x+a2>0]对[x∈R]恒成立，

即有[Δ=（a-1）2-4a2<0]，解得[a<-1或a>13].

所以实数[a]的取值范围为[（-∞，-1）?（13，+∞）].

函数与方程法

不等式、函数、方程三者密不可分，相互联系，相互转化. 求参数的取值范围问题，函数与方程思想是解决这类问题的重要方法.

例2 设[f（x）=x2-2mx+2]，当[x∈[-1，+∞）]时，[f（x）≥m]恒成立，求实数[m]的取值范围.

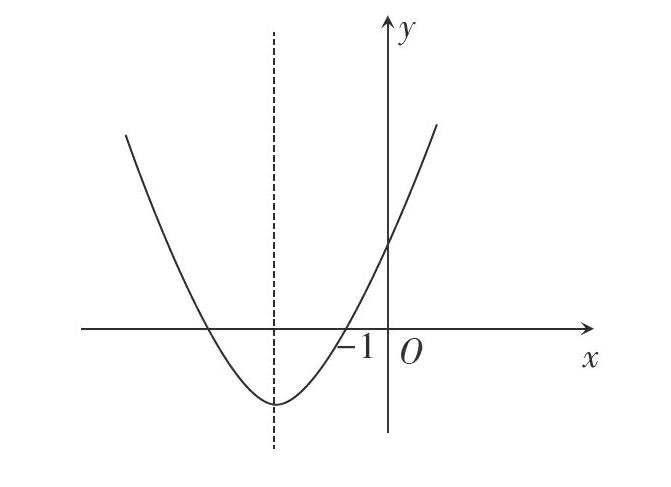
解析 设[F（x）=x2-2mx+2-m]，

则当[x∈[-1，+∞）]时，[F（x）≥0]恒成立.

（1）[Δ=4（m-1）（m+2）<0， 即-20]显然成立.

（2）[Δ≥0]时，如图，[F（x）≥0]恒成立的充要条件为：

[Δ≥0，F（-1）≥0，--2m2≤-1，]解得[-3≤m≤-2].

综上，实数[m]的取值范围为[[-3，1）].

最值法

将不等式恒成立问题转化为求函数最值问题的一种处理方法，其一般类型有：（1）[f（x）>a]恒成立[?af（x）max].

例3 已知[f（x）=7x2-28x-a，g（x）=2x3+4x2-40x]，当[x∈[-3，3]]时，[f（x）≤g（x）]恒成立，求实数[a]的取值范围.

解析 设[F（x）=f（x）-g（x）=-2x3+3x2+12x-c]，

则由题意可知，[F（x）≤0]对任意[x∈[-3，3]]恒成立.

令[F（x）=-6x2+6x+12=0]得，[x=-1或x=2].

而[F（-1）=-7a，F（2）=20-a，]

[F（-3）=45-a，F（3）=9-a，]

∴[F（x）max=45-a≤0]，∴[a≥45].

即实数[a]的取值范围为[[45，+∞）].

分离参数法

若所给的不等式能通过恒等变形使参数与主元分离于不等式两端，将问题转化为求主元函数的最值，从而求出参数范围. 这种方法本质还是求最值，但它思路更清晰，操作性更强. 一般地有：（1）[f（x）f（x）max]；（2）[f（x）>a（a为参数）]恒成立[?a

例4 已知函数[f（x）=ax-4x-x2，x∈（0，4]]时[f（x）<0]恒成立，实数[a]的取值范围.

解析 分离参数，将问题转化为[a<4x-x2x]对[x∈（0，4]]恒成立.

令[g（x）=4x-x2x]，则[a

由[g（x）=4x-x2x=4x-1]可知，[g（x）]在[（0，4]]上为减函数，故[g（x）min=g（4）=0].

∴[a<0]，即[a]的取值范围为[（-∞，0）].

变换主元法

处理含参不等式恒成立的某些问题时，能适时地把主元变量和参数变量进行“换位”思考，往往会使问题降次、简化. 一般来说常将其变换为一次式. 一次函数[f（x）=kx+b（k≠0）]在[[α，β]]上恒有[f（x）>0]的充要条件为[f（α）>0，f（β）>0.]

例5 对任意[a∈[-1，1]]，不等式[x2+（a-4）x+4-][2a>0]恒成立，求[x]的取值范围.

解析 令[f（a）=（x-2）a+x2-4x+4]，则原问题转化为[f（a）>0]恒成立（[a∈[-1，1]]）.

当[x=2]时，可得[f（a）=0]，不合题意.

当[x≠2]时，应有[f（1）>0，f（-1）>0，]解之得[x<1或x>3].

故[x]的取值范围为[（-∞，1）?（3，+∞）].

数形结合法

数学家华罗庚曾说过：“数缺形时少直观，形缺数时难入微”，这充分说明了数形结合思想的妙处，在不等式恒成立问题中它同样起着重要作用. 我们知道，函数图象和不等式有着密切的联系：（1）[f（x）>g（x）?]函数[f（x）]图象恒在函数[g（x）]图象上方；（2）[f（x）

例6 设[f（x）=-x2-4x] ， [g（x）=43x+1-a]，若恒有[f（x）≤g（x）]成立，求实数[a]的取值范围.

解析 在同一直角坐标系中作出[f（x）]及[g（x）]的图象.

如图所示，[f（x）]的图象是半圆[（x+2）2+y2=4（y≥0），][g（x）]的图象是平行的直线系[4x-3y+3-3a=0].

要使[f（x）≤g（x）]恒成立，

则圆心[（-2，0）]到直线[4x-3y+3-3a=0]的距离满足[d=-8+3-3a5≥2].

解得[a≤-5或a≥53]（舍去）.

由上可见，含参不等式恒成立问题覆盖知识点多，方法也多种多样，但其核心思想还是等价转化. 抓住了这点，就能以“不变应万变”.