突发事件下需求依赖价格的三级供应链收益共享契约
2015-08-17庞庆华胡玉露陈华敏
庞庆华 ,张 月 ,胡玉露,陈华敏
(1.河海大学 企业管理学院,江苏 常州 213022;2.常州工学院 计算机信息工程学院,江苏 常州 213022)
当今社会突发事件频发,如2003年“非典”事件、2008年中国南方雪灾、2011年日本大地震、2013年H7N9禽流感等重大突发事件。突发事件对由众多企业所组成的供应链系统造成了重大影响,可能导致供应链系统已制定的生产、存储等计划不再可行,或者已协调的供应链系统不再协调。实践证明:制定出科学的突发事件应对策略,能够有效地提高供应链的运行能力,充分发挥供应链的潜力。因此,研究供应链系统如何提高应对突发事件的能力具有重要意义。
学者们在二级供应链(供应商-零售商)上对如何应对突发事件做了大量的研究工作,也得到了诸多研究成果。Huang等[1]发现,可以利用价格折扣契约来应对突发事件。Xiao等[2]探讨了如何利用线性数量折扣和全数量折扣契约来应对突发事件,之后,Xiao等[3]在制造商的生产费用突变时又对全数量折扣契约和部分数量折扣契约进行了改进以应对突发事件。Chen等[4]在Xiao等的基础上,研究了如何利用线性数量折扣契约和批发价格契约来应对突发事件。于辉等[5-6]对批发价格及数量折扣契约进行了改进,使之具有抗突发事件性,并指出,只有当突发事件造成市场需求变化足够大时,供应商才会调整生产计划并实时启动供应链应急管理。腾春贤等[7]在供应链网络均衡模型的基础上,对数量折扣契约进行了改进,使之具有抗突发事件性。马成等[8]研究了具有抗突发事件性的期权契约。张菊亮等[9]在VMI情形下,提出可以通过未售货物补充契约来应对突发事件。孙亮等[10]和曹二保等[11]探讨了如何应用收益共享契约来应对突发事件。姜丽宁等[12]通过设置目标回扣契约参数,获得了需求突发下集权供应链和分权供应链达到协调时需要满足的条件。覃艳华等[13-14]探讨了如何利用期权契约、回馈与惩罚契约来协调突发事件下的二级供应链。
通过文献检索发现,在三级供应链上研究如何应对突发事件的文献较少。从现有文献上看,王虹等[15]在于辉等[5]的研究基础上,考虑了市场需求变化和额外成本非线性时的两种情形,在三级供应链上提出了具有抗突发事件性的数量折扣契约。胡劲松等[16]和庞庆华[17]分别改进了价格折扣契约和收益共享契约,使之能够在三级供应链上应对突发事件。孙在东等[18]在三级供应链上讨论了如何利用回购契约来应对突发事件。三级供应链相对于二级供应链而言,其协调与运作有着更为复杂的规律,并非2个二级供应链的简单叠加。事实上,现实中的供应链也往往表现为三级及以上结构,这种供应链存在着多个交易过程,受突发事件的影响也更为深刻。因此,必须重视对三级供应链应对突发事件的研究。
然而,在上述三级供应链研究文献中均未考虑到突发事件下销售价格对市场需求的影响。在影响市场需求的诸多因素中,销售价格无疑是最重要的一个因素,现有文献中只有于辉等[19]研究了需求依赖价格情况下突发事件对两级供应链造成的影响,因此,在突发事件研究中也要考虑到市场需求依赖价格的问题。此外,在上述文献研究中,在应对突发事件时提出的契约模型往往都是一种基于数量折扣策略的契约模型,例如文献[10,16]中提出的分别是基于数量折扣策略的收益共享契约模型和基于数量折扣策略的价格折扣契约模型。这种基于数量折扣策略的契约模式是一种混合的契约模式,在企业实施过程中可能由于其过于复杂、监管费用过高等原因而致使无法得到具体应用。
本文以收益共享契约作为研究对象,探讨三级供应链如何应对突发事件。收益共享契约在文献[20-21]中已有详细阐述,这里不再赘述。突发事件发生后往往致使市场需求发生较大变化,进而使得收益共享契约的协调性受到限制。在市场需求是随机的且依赖销售价格的情形下,本文的主要创新点体现在:①在三级供应链上探讨了如何制定应对突发事件的策略,提出了具有抗突发事件性的收益共享契约,包括基于数量折扣策略的收益共享契约和纯粹形式的收益共享契约两种形式;②突发事件发生后,在市场需求与销售价格分别满足加法和乘法形式时,给出了供应链系统最优产品订购量和最优销售价格的确定方法。
1 问题描述与条件假设
Cachon等[20]曾指出,尽管报童模型较简单,但已足够用来研究供应链契约。在已有三级供应链研究中,均是以报童模型作为基础进行建模分析的。本文在模型构建时也是以报童模型为背景进行的,即供应链成员均是理性的,都以自身期望收益最大为原则进行决策的。并假定制造商生产能力不受限制,能够根据订单来进行产品制造和供应;供应链成员均无资金约束,能够根据市场需求或下游成员的订单来进行订货。显然,对于理性的制造商和分销商而言,为了使得自身收益最优,其订购量(制造量)必然与零售商的订购量相同。
假定cm、cd、cr分别为制造商(m)、分销商(d)和零售商(r)获得单位产品的边际成本,为简单起见,令c=cr+cd+cm;υ为单位剩余产品的残值与分别为分散决策模式下和收益共享契约模式下,上游成员(制造商和分销商,即i=m,d)给予其下游成员(分销商与零售商,即i=d,r)的批发价格;Q为产品订购量;p为市场销售价格;x为零售商面临的随机市场需求,且受到市场销售价格的影响,其对应的需求概率密度函数和需求分布函数分别为和F,其中连续可微;由于市场需求是价格因素的减函数,故∂F)/∂p>0,即随着价格的增加,市场需求是一个相对于p的随机减函数;S(Q,p)为给定订购量和销售价格下的期望销售量,即

剩余产品的期望数量为I(Q,p),且I(Q,p)=Q—S(Q,p)。
突发事件发生后,容易造成市场规模扩大或缩小。例如,“非典”发生后,市场对口罩的需求明显上升;“禽流感”发生后,市场对活鸡等禽类的需求明显下降。当突发事件造成市场规模扩大时,此时对于制造商和分销商来说,要启动准时制生产方式和紧急运输方式,会产生一定的成本;当突发事件造成市场规模缩小时,显然将出现较多的剩余产品,对于供应链各成员来说,都要承担一定的费用。这里假定αi为突发事件发生后市场规模变大而增加生产,导致分销商(i=d)和制造商(i=m)带来的单位产品处理成本,令α=αd+αm;βi为突发事件发生后市场规模变小,导致零售商(i=r)、分销商(i=d)和制造商(i=m)处理剩余产品而带来的单位成本,令β=βi+βd+βm。
2 收益共享契约下的供应链协调
考虑市场需求依赖销售价格情形下,这里分析能够使得三级供应链协调的收益共享契约模型。假定制造商提供给分销商、分销商提供给零售商的收益共享契约参数分别为(,φ1)和,φ2)。为了便于分析,认为分销商与零售商都接受了该契约,则此时供应链系统与供应链成员的期望利润分别为:
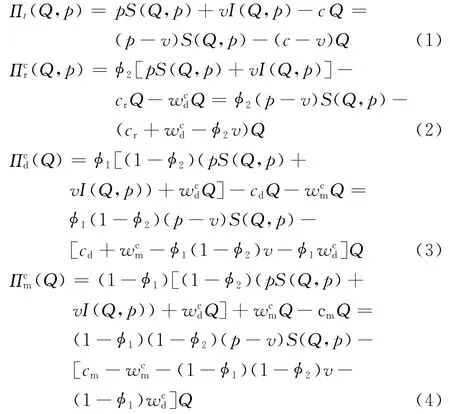
命题1当和满足式(5)时,收益共享契约能够使三级供应链协调。
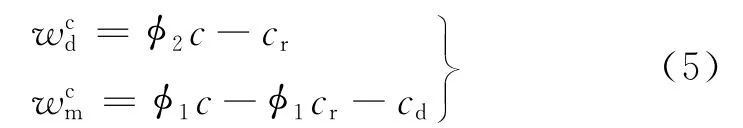
证明比较式(1)、(2),易得

则满足式(2)的最优销售价格必然满足式(1),即在收益共享契约下零售商的最优销售价格也是集中决策模式下供应链系统的最优销售价格。
对于供应链成员而言,在收益共享契约下需要考虑如何制定决策使得自身收益最优。对零售商而言,在接受分销商提供的契约(,φ2)后,其决策变量为自身订购量和p;同样,对分销商和制造商而言,其决策变量分别为自身的订购量和。
收益共享契约若使得三级供应链协调,一个必要条件就是零售商的最优订购量与供应链系统的最优订购量相等,即

另外,根据本文的假设,对于理性的分销商和制造商而言,在收益共享契约协调下,为了获取最大利润,其最优订购量(生产量)必然要与零售商的最优订购量相等,即

即在收益共享契约下,为描述方便,令=Qt=Q。
结合式(1)~(4),从而易得式(5)。将式(5)代入式(2)~(4),又可得:
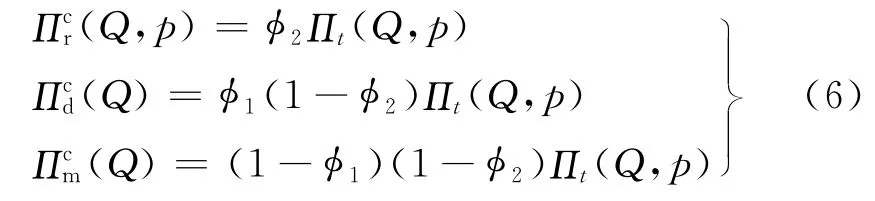
由式(6)可见,此时的收益共享契约能够使得供应链协调,供应链成员能够依据上述公式来分配供应链系统的利润。 证毕
命题1说明,当和满足式(5)时,收益共享契约能够协调三级供应链。但事实上,要使供应链成员愿意采用收益共享契约,那么其采用收益共享契约之后的收益必然不能低于其在分散决策模式下的收益,故在供应链实践中还需考虑这一参与约束条件,即对供应链成员而言,应分别满足:
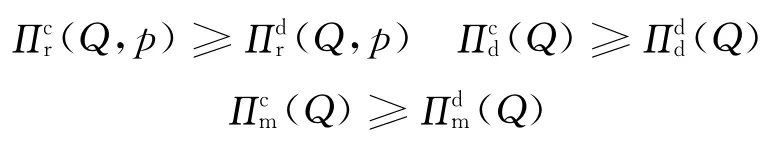
其中。上标d表示分散决策模式。从参与约束条件中,可得收益分享比例φ1和φ2需满足的条件为:
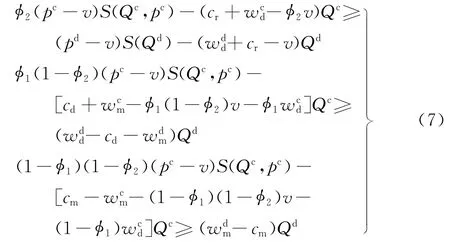
式中:Qc和pc分别为收益共享契约下零售商的订购量和产品销售价格;Qd和pd分别为分散决策模式下零售商的订购量和产品销售价格。由于式(7)较为繁琐,故在本文的后续论述中不再一一探讨收益分享比例φ1和φ2需要满足的参与约束条件。
在一般情况下,与取值是非负的,且φ1,φ2∈(0,1),因此,得到收益分享比例φ1和φ2还需要满足的条件为:

3 突发事件下的供应链协调
3.1 突发事件对供应链协调的影响
对于已协调的供应链系统来说,在销售周期开始前,供应链成员根据收益共享契约来制定最优的订购量Q*和最优的销售价格p*,并安排相应的生产经营活动。然而,突发事件往往导致市场需求发生重大变化,在此情形下,原来的最优订购量Q*和最优销售价格p*并不一定是突发事件发生后供应链成员的最优决策。这里假定突发事件发生后,市场需求分布函数由F(xp)变化为G(xp),相应的市场需求概率密度函数由f(xp)变化为g(xp)。则此时供应链系统的利润函数可以写为

如果此时仍然采取原来的收益共享契约来协调供应链,即收益共享契约参数满足式(5),则此时零售商、分销商和制造商的利润函数分别为:
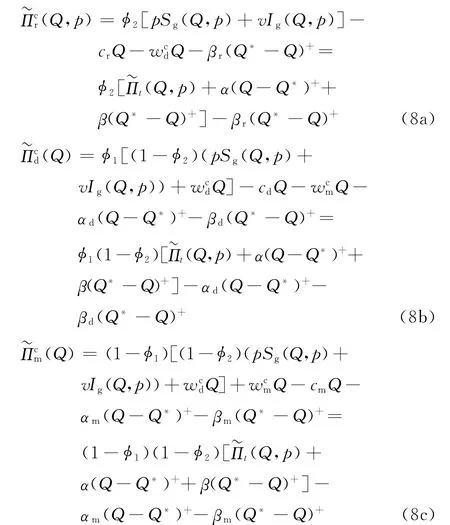
由式(8a)~(8c)可见,此时供应链成员的利润函数与供应链系统的利润函数不再具有线性关系,即不再是供应链系统利润函数的仿射函数。这说明,在突发事件发生后,原来的收益共享契约无法使得此时的供应链协调。
3.2 具有抗突发事件性的收益共享契约
3.2.1 基于数量折扣策略的收益共享契约 由式(8)可见,突发事件对供应链的协调状态造成了影响,使得已协调的供应链不再协调。文献[5-6]中表明,如果供应链成员的利润函数为供应链系统利润函数的仿射函数,则此时供应链是协调的。因此,在突发事件发生后,使供应链恢复到协调状态的一个简单作法就是让供应链成员的利润函数为供应链系统利润函数的仿射函数。命题2就给出了这种基于数量折扣策略的收益共享契约形式。
命题2假定契约参数满足:
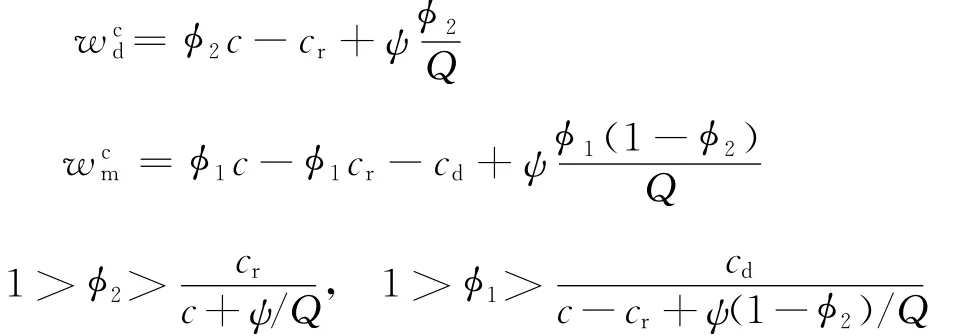
其中,ψ=α(Q—Q*)++β(Q*—Q)+。则此时经过调整的收益共享契约能够使得三级供应链协调。
证明突发事件发生后,供应链系统的利润函数为(Q,p)。将分别代入式(8),可得:
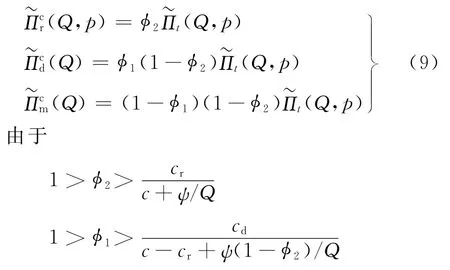
故可保证与取值满足非负性约束。
显然,此时零售商、分销商和制造商的期望利润函数是整个供应链系统期望利润函数的仿射函数,因此,经过调整之后的收益共享契约能够使得三级供应链协调。 证毕
需要指出的是,式(9)给出的是一种类似于式(6)的形式,目的是为了便于同未发生突发事件的收益共享契约做比较。事实上,和的数量折扣形式并非一定如命题2表述得那样,可能具有其他多种数量折扣形式。
3.2.2 纯粹的收益共享契约 在3.2.1小节中,所提出的收益共享契约是一种基于数量折扣策略的混合模式。由于存在其形式表达较为繁琐与监管费用较高等问题,致使这种混合模式有可能在实践过程中无法得到顺利实施。本小节提出一种纯粹的具有抗突发事件性的收益共享契约。
命题3假定契约参数满足:

其中:

则此时经过调整的收益共享契约能够使得三级供应链协调。
证明由于
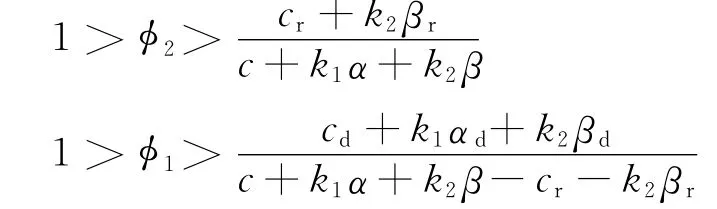
故可保证与取值满足非负约束
(1)若突发事件发生后导致市场规模扩大,此时有
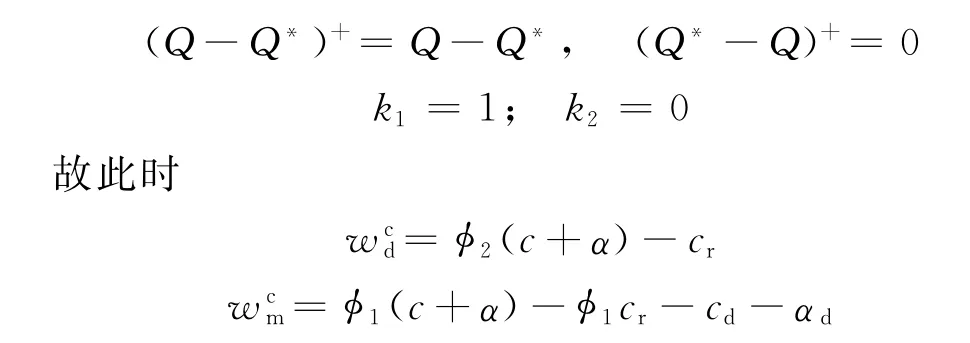
将分别代入供应链成员的利润函数,可得:

(2)若突发事件发生后导致市场规模缩小,此时有
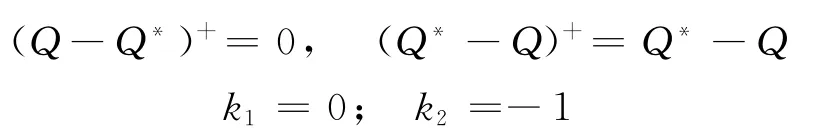
故此时

将分别代入零售商、分销商与制造商的利润函数,得:

综合(1)和(2)两种情况来看,突发事件无论是导致市场规模扩大还是缩小,此时零售商、分销商与制造商的期望利润函数依然是整个供应链系统期望利润函数的仿射函数,因此,当契约参数满足命题3时,经过调整之后的收益共享契约能够使得三级供应链协调。 证毕
在突发事件发生后且市场需求依赖于价格时,本文提出的基于数量折扣策略的收益共享契约和纯粹形式的收益共享契约都能使得三级供应链协调,也从而表明这两种改进的收益共享契约具有抗突发事件性。
4 突发事件下的收益共享契约优化策略
由上文可以看出,本文改进的收益共享契约能够应对突发事件,具有抗突发事件性。本节要解决的是当突发事件发生后如何确定供应链系统的最优订购量和最优销售价格。
当市场需求依赖价格时,一般有两种表达方式:加法形式X(p,ξ)=y(p)+ξ和乘法形式X(p,ξ)=y(p)ξ。其中ξ是独立于p的随机变量,且0<A≤ξ≤B,其概率密度函数和分布函数分别为f(ξ)和F(ξ);y(p)在区间上连续非负且二阶可导与分别为允许的最小和最大销售价格。由于y(p)是p的减函数,故dy(p)/dp<0。
命题4突发事件发生后,对于给定的销售价格p:
(1)如果市场需求满足加法形式X(p,ξ)=y(p)+ξ,则整个供应链系统的最优订货量满足,其中,

(2)如果市场需求满足乘法形式X(p,ξ)=y(p)ξ,则整个供应链系统的最优订货量满足,其中,

证明这里给出突发事件引起市场规模变大的证明,市场规模不变或变小可参照此证明过程。假定突发事件使得市场规模变大,则供应链系统的利润函数改写为

(1)当市场需求满足加法形式X(p,ξ)=y(p)+ξ时,则此时市场需求X(p,ξ)的分布函数可以写为G(x|p)=G(x—y(p))。其中,
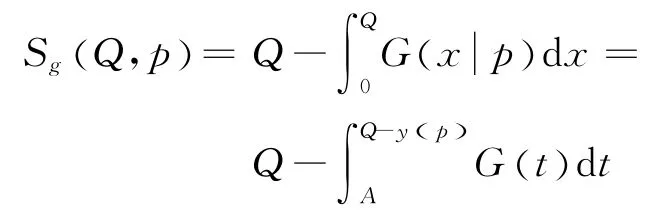
故供应链系统的收益函数改写为

由式(15)易得:
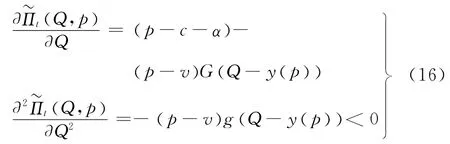
即对于给定的销售价格p(Q,p)是Q的凹函数。故此时最优解应满足其一阶导数为0的条件,即

(2)当市场需求满足乘法形式X(p,ξ)=y(p)ξ时,则此时市场需求X(p,ξ)的分布函数可以写为
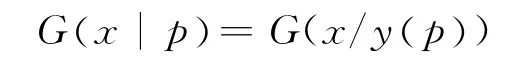
其中,

故此时供应链系统的利润函数改写为

易得:

即对于给定的销售价格p(Q,p)是Q的凹函数。故此时最优解应满足其一阶导数为0的条件,即

命题5突发事件发生后,无论市场需求满足加法形式X(p,ξ)=y(p)+ξ还是满足乘法形式X(p,ξ)=y(p)ξ,只要ξ满足增加的通用失败率(IFGR),y(p)满足增加的价格弹性(IPE),则在区间是p的 拟 凹函数。
命题5的证明类似于文献[22],这里省略。
命题6突发事件发生后,
(1)当市场需求满足加法 形式X(p,ξ)=y(p)+ξ时,供应链系统的最优销售价格由式(21)唯一确定。
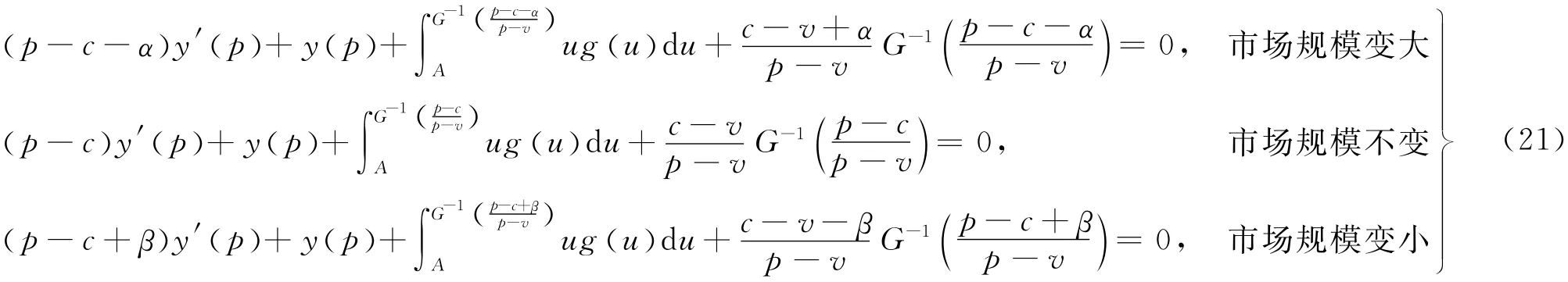
(2)当市场需求满足乘法形式X(p,ξ)=y(p)ξ时,供应链系统的最优销售价格由式(22)唯一确定。

证明这里仍然给出突发事件引起市场规模变大的情形,其他情形可参考本证明过程。
(1)当突发事件发生后,市场需求满足加法形式X(p,ξ)=y(p)+ξ时,则由命题4知,


有唯一最优解p*。
(2)当突发事件发生后,市场需求满足乘法形式X(p,ξ)=y(p)·ξ时,则由命题4知,


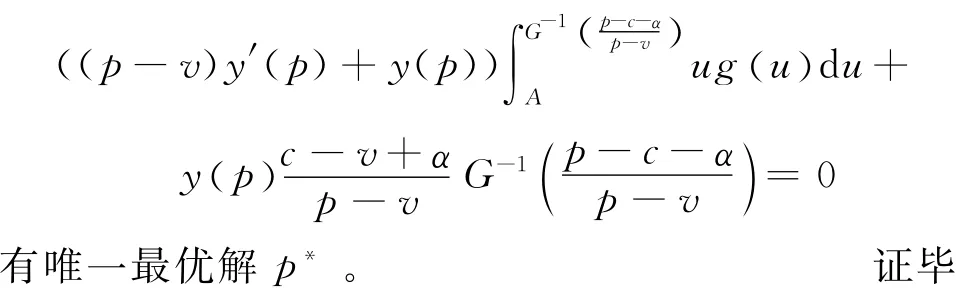
显然,通过命题6发现,当突发事件发生后,供应链系统的最优销售价格有所变化。对于零售商而言,为了取得自身利润最大化其也需对自身的销售价格做出调整。假设零售商调整价格来更好地应对市场需求的变化,由于其单独承担价格调整的成本,此时命题2、3设计的收益共享契约将不再使得供应链协调。故可以考虑零售商、分销商和制造商按照一定比例承担其价格变动的成本。为了进一步使得供应链能应对突发事件并保持协调,提出如下收益共享契约。
命题7若突发事件发生后,零售商调整自身的销售价格来更好的应对市场需求。假设零售商单独承担价格调整的成本Γ,则如下的收益共享契约可以协调需求依赖价格的三级供应链,并能用来应对突发事件。
(1)假定分销商给零售商、制造商给分销商分别提供的收益共享契约参数为(),(),且契约参数满足如下条件:
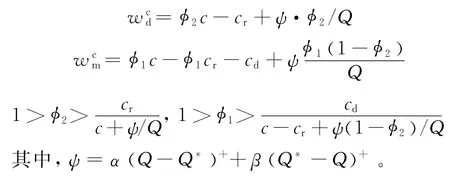
(2)当零售商调整其销售价格时,分销商给予零售商(1—φ2)Γ的补助;而制造商给予分销商(1—φ1)(1—φ2)Γ的补助。
5 数值分析
假定某供应链由零售商、分销商与制造商组成,他们之间缔结了收益共享契约。成本参数:υ=3,cr=1,cd=2,cm=5,=5,=8。
假定突发事件发生前市场需求满足加法形式,且y(p)=450—10p,ξ在区间[50 ,100]均匀分布,易知,此时有:

突发事件发生后,市场需求仍然满足加法形式,但此时y(p)=300—10p,ξ在区间[30 ,70]均匀分布,同理易知,此时有:

为了便于分析,假设对于供应链成员来说,均有αd=αm=βr=βd=βm=1。
(1)突发事件发生前,此时对于集中决策下的供应链系统,有

由图1可见,∏t(Q,p)为p的拟凹函数。容易求得此时供应链最优销售价格p*=30.21,最优订货量Q*=239,供应链系统利润∏t(Q*,p*)=4 848.6。

图1 突发事件前供应链利润与销售价格的关系
(2)突发事件发生后,此时对于集中决策下的供应链系统,有


图2 突发事件后供应链利润与销售价格的关系
综上可见,由于突发事件造成市场规模的变小,使得此时供应链系统的利润有了明显下降,故用契约来协调供应链显得尤为必要。
表1给出了在突发事件发生前后,供应链系统在不同情形下的各个参数(此时假定φ1=0.5,φ2=0.45)。由表1可见,突发事件对供应链系统的运营的确造成了极大的影响。如果三级供应链在应对突发事件时,采用调整之后的收益共享契约则可以激励供应链成员积极参与供应链运作,充分发挥供应链的潜力,进而提高供应链系统的订购量和总利润。

表1 需求与价格相关下突发事件发生前后供应链系统的参数比较
同样可知,在应对突发事件的收益共享契约下,零售商、分销商与制造商的利润不同程度地受到契约参数的影响。如要保证收益共享契约的顺利实施,则除了实现全局协调之外还需要保证契约式供应链中各节点企业的利润不低于他们不采用契约时的利润,即对于契约参数还需要进行限制取值,这里不再举例。
6 结论
突发事件对供应链契约协调造成了重要影响,可能导致已协调的供应链不再协调。如何应对突发事件是供应链契约研究中一个亟需解决的问题。本文以收益共享契约为对象,在三级供应链的基础上探讨了突发事件对收益共享契约协调性的影响,得到如下结论:
(1)未发生突发事件时,在市场需求是随机的且受到销售价格影响的情况下,收益共享契约能够使得三级供应链协调,但契约参数要满足一定的约束条件。
(2)当突发事件发生后,市场需求发生了变化,原来的收益共享契约无法使得现有供应链协调。原因在于,突发事件可能造成一定的紧急生产费用或者剩余产品处理费用等,而在原来的收益共享契约中并未考虑到这一情况。
(3)本文提出了两种具有抗突发事件性的收益共享契约形式:基于数量折扣的收益共享契约形式和纯粹的收益共享契约形式。从理论上看,基于数量折扣的收益共享契约形式较为简单,但由于这是一种混合的契约形式,在实施中可能存在较高的监管费用等情况,故在企业实践中纯粹的收益共享契约形式可能更受供应链成员的欢迎。
(4)在考虑了市场需求与价格满足加法形式和乘法形式后,对改进的收益共享契约模型进行了优化分析,给出了确定最优订购数量和最优销售价格的方法,为企业开展实践工作奠定了理论基础。
当然,本文是在风险中性的情况下进行探讨的,现实中,供应链成员对待突发事件的态度明显不同,存在着各自的决策偏好。因此,在下一步的研究中需要考虑决策偏好等更加复杂的情况。
