Zipf定律及Zipf语言经济论剖析
2015-08-17洛阳师范学院
洛阳师范学院 丁 政
Zipf定律及Zipf语言经济论剖析
洛阳师范学院 丁 政
Zipf认为,因言者与听者的行为均受最小努力原则支配,双方立场上的省力是一对矛盾,基于言者经济的单一化力量与基于听者经济的多样化力量交锋,造就了语流中词语的一种规则的分布格局,即被后人称为Zipf定律的序号频率分布律(rank-frequency distribution)。然而,根据已达成共识的相关数学研究,Zipf定律另有原理。Zipf的语言经济论因此失去了一项其赖以成立的证据。不仅如此,语言学理性审视下,Zipf语言经济论实则远非无懈可击。立足语言学视角,本文欲解决两个问题:其一,以力求直观的方式对Zipf定律一探究竟,明确该定律并非Zipf所谓两种力量或言者听者双边经济矛盾的产物;其二,为Zipf语言经济论提出去伪存真的评价。
Zipf定律、最小努力原则、语言经济论
1. 引言
为现代语言研究打开新局面的趋势之一是具有人文传统的语言学与数学、统计学相结合。语言经济思想的奠基者之一,美国语言学家George Kingsley Zipf就是这种研究范式的先驱者之一。Zipf最为世界所熟知的研究成果莫过于Zipf定律与最小努力原则。Zipf定律是最早提出的计量语言定律之一,究其来龙去脉,在前人成果的基础上,Zipf以大量数据对该定律加以验证,将其纳入语言经济研究以及人类生态学范畴。最小努力原则是Zipf毕生治学历程的结晶,这一历程始于他对人类语言用词经济效应的钻研,以其对用词经济之心理本质的哲思为积淀,最终归于人类行为的基本规律。Zipf(1949)在著作《人类行为与最小努力原则:人类生态学引论》中提出最小努力原则。这部著作可谓Zipf毕生研究成果集大成之作,是人类生态学理论的重要组成部分。该书构建了以最小努力原则为纲的语言经济论,并且他先前在用词经济性研究中取得的重要成果均被重新诠释,Zipf定律就是其中之一,该定律原名为“词语序号频率分布(rank-frequency distribution of words;以下简称序频分布律)”(同上:25),本是Zipf用于论证其语言经济理论的一项实证依据。出于语言之混沌,自然文本词语的序号频率分布却呈现一种耐人寻味的规则格局,加之序频分布律在1949年著作的后半部分被Zipf推广应用于社区规模、城市人口等领域,Zipf的实证定律引起了科学界的浓厚兴趣与广泛关注,并被后人称为Zipf定律、Zipf分布。
2. Zipf语言经济理论之精髓
2.1 最小努力原则与语言经济机制假说
在《人类行为与最小努力原则:人类生态学引论》一书开篇,Zipf提出了最小努力原则,指出人类行为普遍受这一基本原则支配。最小努力之实质包括两个层面:其一,最小努力是“最小工作量的一种变体”(Zipf 1949:1);其二,最小努力是一种平均量。也就是说,人的行为不可能时时处处都做到最小努力,但行为路径之多个步骤、解决系列问题之多个过程的平均工作量趋于最低。此外,以斧锯刨凿与木匠活、战时转产军车的民用汽车厂等例子作比,Zipf(同上:8)为人类行为打了一个比方,或者说建构了一个用以表述人类行为的模型,即工具与任务关系:在最小努力原则支配下,工具与任务之间相互选择、相互依存;一方面,工具适应任务才能有效降低工作量;另一方面,执行何种任务能够达成最小努力又取决于已经掌握的工具。
提出最小努力原则后,Zipf(同上:19)明示:他对人类行为生态的研究首先关注人的语言行为;对语言行为的探讨始于将人类言语视为一系列工具的组合,具体而言,将词汇看作一系列工具的组合。基于这个工具任务关系,Zipf(同上:20-21)提出如下概述的假说。其一,语言中存在一种经济机制、一种潜势,以或多或少尽量俭省的方式将词语与意义结合起来。其二,从言者立场看,使用一个工具完成所有的任务最经济,也就是仅使用一个词语就能表达所有的意义;在听者立场上,因为要在特定语境中解读言者使用的词语,所以最省力的方式是每个词语仅表达一个意思。其三,Zipf构想了“单一化(unification)”与“多样化(diversification)”两种力量,分别基于言者立场与听者立场,单一化力量趋于将词汇的数量减少至一词,而多样化力量则趋于将每词表达的意义缩减到一个,两种力量的交锋决定了语流中存在多少词语以及词语承载多少意义。
2.2 序频分布律与意义分布律
对于其语言经济论中的假说,Zipf进行了如下概述的论证:假设存在两种矛盾经济、两种相对的力量,或许会造就某种“词汇平衡(vocabulary balance)”。“词汇平衡”为何物?Zipf(同上:22)如是说:“我们显然尚不知道在假想的两种力量之间是否真的存在这样一个状态”。可见所谓“词汇平衡”,除字面意思外并无其他内涵。在这种典型的Zipf式论述逻辑中,他提出了“词汇平衡的实证依据”(同上:24),即被后人称为Zipf定律的序频分布律。基于小说《尤利西斯》的词频表,Zipf指出:将构成文本的词语按频率降序排列,词语在词表中的序号r与其相对频率f的乘积约等于一个常数C,即r×f=C。在双对数(log-log)坐标系中,序号频率关系图像呈45度角下倾直线形状,其低频部分呈阶梯状(同上:24),简图示例如图1:
Zipf将45度角下倾直线形状的序频分布看作所谓词汇平衡以及两种力量之说的证据。至于该证据是否充分,Zipf的解释相当单薄:序频分布图像的作图方式是将数据点标于图中,绘图前没有关于图像是否规则的预期,若以线段将数据点连接起来,这些线段的角度随机,但绘图后发现这些随机线段的倾斜方向如此规则,所以词频分布势必受到某种原则的支配(同上:27)。后有学者就序频率分布图像的倾角补充了如下解释:
“如果一种语言只有一个单词,它的出现率会是100%。相反,如果每个单词都只有一个意义,那么,一个语篇的不同单词数会跟总词数一样,而且各个单词的出现次数都会是1。如果用坐标表示,前者是一条竖线,后者是一条横线。把它们合在一起,正好构成一个90度直角。现在的45度斜线,恰恰是前两种情况的中和、妥协。既然前两种情况分别只考虑了说话人利益,或听话人利益,那么,中和前两种情况的第三种情况就既考虑了说话人利益,又考虑了听话人利益,就是‘单一化力量’和‘多样化力量’之间平衡、妥协的结果”(Poosala 1997,转引自姜望琪 2005:90)。
假想的一纵一横两直线何以至于在客观数据之对数坐标系图像中构成45度角下倾直线?以近乎栩栩如生的意象思维臆测语言问题的道理,有违最基本的科学严谨,以上这段解释非但不能支持Zipf的理论,反而更令人生疑。从两种力量到45度角斜线,这个由前后相扣的假说、不甚严密的论证构成的理论体系实则捉襟见肘,下文“Zipf语言经济论献疑”一节将在理性思辨的基础上批判其中破绽;至于Zipf定律规则的图像奥秘何在,下文“Zipf定律原理剖析”一节将有透彻探讨。
Zipf对两种力量之说的论证并未止于序号频率分布,序频分布律还有一个称为“意义分布律(law of meaning distribution)”的姊妹篇:既然词频分布规则,那么意义分布很可能也是规则的;两种力量的交锋之下,不存在能够表达一切意义的词语,但势必有一些词语能够表达多种意义;设文本中最高频词语的频次为F1,该词语表达意义的数量为m1,则m1×f1=F1,其中f1是以该词语表达各意义的平均频率。因单一化与多样化力量的平衡,m1与f1趋于相等,由此,,下标r指的是词语在词频降序排列中的序号;在横轴为r、纵轴为mr的双对数坐标系中,预期得到一条斜率为-0.5的直线(Zipf 1949:28)。对于这个假设,Zipf的实证检验采用Thorndike(1932)汇编的《教师20,000词词书》作为资料,该词书以500为单位分组,并按照词频降序排列。Zipf记录了Thorndike词表中每组词的词典义项数量,按组求得词均意义数量并绘制图像。据Zipf对绘图结果的总结,得到了一组线性排列的数据点,图像线性斜率接近-0.5(Zipf 1949:30)。
Zipf的意义分布律与统计检验缺乏说服力。其一,Zipf调查的是r~m关系,意义分布律公式陈述的是F~m关系,两者显然不能等同。其二,即便不深究前述这个破绽,必须充分论证r~m关系的线性斜率确实趋近-0.5才能为两种力量之说提供令人信服的证据。所以,基于一个不甚严密的模型,用一次性的统计调查验证一个玄虚有加的假说,Zipf的意义分布定律假说经不起推敲。不过,Zipf的实证调查并非乏善可陈,推究意义分布律的前因后果,可溯及Zipf(1945:251)曾提出的一个称为“频率意义律(meaning frequency law)”的用词经济法则:频用词语趋于具有更丰富的多义性。不难看出,意义分布律是频率意义律在以最小努力原则为纲的语言经济论之下的再诠释。Zipf的统计调查不足以支持意义分布律,却是频率意义律与用词经济效应的确凿证据。
限于本文主旨,对Zipf著作的详解止于观研Zipf语言经济论的精髓部分以及Zipf独特的论述模型:与其他人类行为一致,语言行为中的经济性无外乎最小努力;人类言语行为被解读为工具(词语)与任务(意义)的关系;语言经济之最小努力机制是言者与听者的经济对立、单一化与多样化两种力量的交锋与平衡;序频分布律、意义分布律既是这种机制的现象,也是其证据。然而,正如上文已经提出的若干评论,Zipf的语言经济论由双边经济论、两种力量论等假说构成,而Zipf对其假说的论证远非无懈可击。因此,Zipf语言经济论遗留了一些值得商榷的问题:如何评价Zipf的假说?Zipf的实证定律能否作为这些假说的确凿支持?
3. Zipf定律原理剖析
3.1 “于语言而论,Zipf定律甚浅”
为解答Zipf定律是否即所谓词汇平衡、是否是两种力量之确凿证据的问题,不免涉及关于Zipf定律的数学研究。统计语言学家Herdan(1966:33)指出:“语言学家认为Zipf发现了一个数学定律,而数学家认为Zipf发现了一个语言学法则”。经由此话,Herdan表达了一种主张:在Zipf定律这个问题上,语言学与数学两个视角应互通有无,否则语言学家有可能对Zipf定律的数学本质不求甚解,而数学家为Zipf定律建立的解析模型未必符合语言实情。
Zipf本人关于Zipf定律原理的看法,即最小努力原则造就了Zipf定律,并没有得到广泛认可。数学家Mandelbrot,心理学家、语言学者Miller早已通过数学研究为该定律道破玄机,Miller贡献的启示更加斐然。Mandelbrot率先提出了Zipf定律的数学论证以及数学推广,即Zipf-Mandelbrot定律。Mandelbrot的研究显然受到最小努力原则的启发,使用了一个抽象晦涩的“单位信息最小平均成本”模型(转引自Miller 1957:313)。Miller(同上:311)沿用前者的数学模型,为其破除玄虚,提出Mandelbrot模型的一种直观解释,即“猴文本(monkey text)”。“猴文本”可解读为:猴子任意敲击打字机键盘,产生随机字母组合,随机出现的空格将字母组合切分为形式词符,形式词符堆砌产生形式文本。基于这一模型,Miller成功完成数学推导并得出结论:“简单无奇的数学过程便能够产生Zipf定律,无需为最小努力、最小成本之类原则建模”(同上:313)。猴文本研究后Miller曾多次发表旨在为Zipf定律去伪存真的看法,在为Zipf著作之再版撰写的导读中如此评价Zipf的研究:
“面对Zipf定律的数学秩序性,选择无非有二:或以人类心理的某种共同属性解读定律,或视其为某种概率规则的必然结果。Zipf的选择是制造假说,试图以最小努力原则去解释用词行为中在似是而非的单一化与多样化之间的某种平衡。其他人则大多寻求基于概率原理的解释。三十多年的研究后,这个问题已经明朗,后者才是正确的。视消息源为一个随机过程,Zipf曲线所描述的无非是该过程的必然结果”(Miller 1965:vi)。
Miller & Chomsky(1963:463)也曾指出:“Zipf定律并不能说明存在某种能够塑造人类语言交流行为的普遍心理作用”。Mandelbrot (1982:346)后来也承认最小成本的概念并无必要,并提出一句言简意赅的评论:“于语言而论,Zipf定律甚浅”。该如何理解Mandelbrot的这句话?人的身高是典型的正态分布总体,但不能从身高的生物学基础为正态分布钟形曲线找原因。同理,Zipf定律确系语言之特征,但并非语言之特有,至于Zipf曲线何以呈现规则形态,并非一个语言学问题,而是一个数学问题。
3.2 Zipf定律成因之直观模型
本文无意深入Zipf定律的数理分析,仅希望通过一种较直观的方式阐明“于语言而论,Zipf定律甚浅”的道理,不妨从猴文本说起。猴文本是一个用于数学论证的模型,与自然文本有很大的区别,如下是一个模拟猴文本并分析其词语序频分布的R语言程序以及该程序输出的图像实例:
#程序1
alph="_ABCDEFGHI"
#代码清晰起见,以下划线表示空格
#以连字符表示字母间无空格
alph=unlist(strsplit(alph,split=NULL))
txt=paste(sample(alph, 50000, replace = TRUE),collapse="-")
ws=unlist(strsplit(txt,"_"))
ft=table(ws[which(ws!="-")])
ft=data.frame(ft)
f=sort(as.numeric(ft[[2]]),TRUE)
r=seq(1:length(f))
plot(log(r),log(f))
程序1的原理与步骤正如本文上节对猴文本模型的解释,凭经验斟酌,设置了一个短小的字母表,生成尽可能接近自然文本的猴文本序频分布。尽管有所干预,程序1生成的序频分布(如图2)与自然文本的Zipf分布(如图1)相去甚远,但也显现出整体格局的相似,这说明形式上的自然文本与猴文本本质相通,所以不妨以后者为启发,构思一个更接近自然语言的模型。
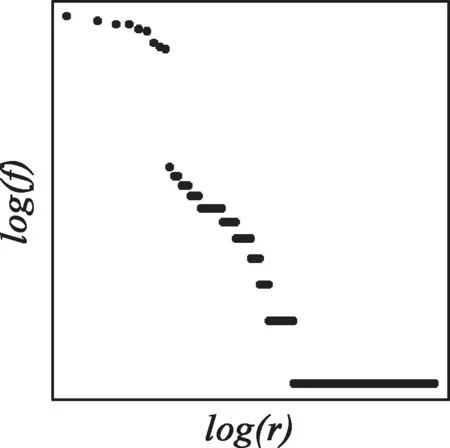
图2. 猴文本序频分布
猴文本的形式词符是随机字母组合,短者概率高,长者概率低,合乎自然语言词符参差不齐的使用概率;猴文本可看作一个概率随机模型,自然语言由词符构成语句的形式过程理论上也是如此。所谓概率随机,直观起见,以投掷骰子作比。将一枚骰子看作一个消息源,其符号表含6个词语,概率均为1/6,连续掷骰子的过程就是以此系统产生文本的随机过程。由自然语言词符构造语句的过程与连续掷骰子相似,具有很高的随机性。而自然语言词符的概率分布参差不齐,封闭类词语的使用概率普遍高于开放类词语,后者之列也有较常用、较不常用的概率之别。基于上述原理,设计了如下R语言程序,输出模拟序频分布图像:
#程序2
nw=50000;st=50000
#词表长度与形式文本长度
mean=1;stdv=exp(1)
#对数正态分布参数(凭经验斟酌)
ws=as.character(seq(1:nw))
rn=rlnorm(nw,mean,stdv)
p=rn/sum(rn)
txt=sample(ws,st,TRUE,p)
f=sort(table(txt),TRUE)
f=as.numeric(f)
r=seq(1:length(f))
plot(log(r),log(f))
盒马鲜生创始人侯毅在“双十二供应链升级沟通会”上表示,“我们进入不同城市后发现,一二三线城市的消费习惯、消费水平差异较大,包括主城区和郊区等差距都很大。这就促使我们需要分层经营、分类经营。可以说原来是舍命狂奔、现在要精细化运营。”
程序2细节如下:(1)假设以数量为50,000的词符集作为消息源,生成长度为50,000的随机文本;(2)对于消息源的概率分布,采纳Herdan(1960:42)的理论:“词频分布总体受对数正态分布律支配”,假设消息源服从对数正态分布。凭经验斟酌其参数,选择1为均值,以自然常数e为标准差;(3)从这个消息源连续随机采样50,000次,相当于在一个概率随机过程中生成如此长度的随机文本,对随机文本进行频率分析后绘制序频关系的log-log图像。以下是程序2运行结果的一个实例:
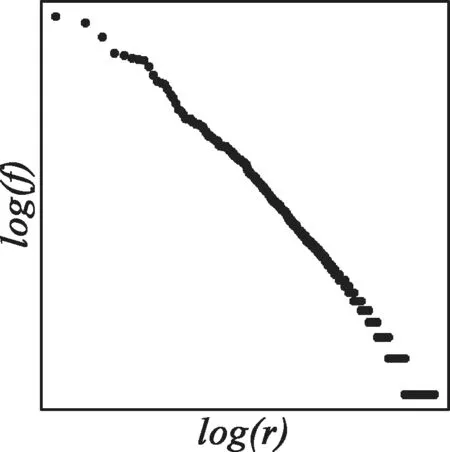
图3. 模拟自然语言形式文本序频分布
由图3可见,程序2模拟自然文本Zipf分布的效果显然优于程序1,在目测之下与自然文本Zipf曲线(如图1)相差无几,足以印证Miller所谓“简单无奇的数学过程就能够产生Zipf分布”。程序2的原理无外乎从对数正态分布总体随机采样,与猴文本模型一样简单无奇,且更符合自然语言形式上的语句构造过程。
3.3 关于Zipf定律系数的研究
根据Joos、Mandelbrot等学者的研究(详见冯志伟 1983),Zipf序频分布律原公式缺乏普遍性,有失精确。实际应用中的Zipf定律公式是Zipf原公式的修正与推广,可写作rBf=C,Zipf原公式是当B=1时修正公式的特例。修正公式中B、C是两个系数,并非两个常数。因为目测下形似斜线,Zipf分布被看作log-log坐标系中的线性关系,由修正公式可推得:log(f)=log(C)-B(log(r))。该线性关系的截距是log(C),其斜率是-B。不过,Zipf分布实质上比双对数线性关系更复杂,尚无明确的线性拟合截距取值标准,C取值不定,而B的测定一般采用最大似然估计(MLE)方法。以下程序中的B.MLE是基于MLE且专用于计算Zipf定律系数B的R语言函数:
#程序3
B.MLE<-function(f)
{library(stats4)
LLH=function(B){
r=seq(1:length(f))
L=B*log(r)+log(sum(r^-B))
sum(f*L)}
fit=mle(LLH,start=list(B=-1))
B=as.numeric(fit@coef)
return(B)}
f = scan("data.txt")
#数据文件格式是空格分隔的自然数词频
B.MLE(f)
采用MLE方法对多个英文语料库的Zipf定律系数实施精确测定,结果见下表:
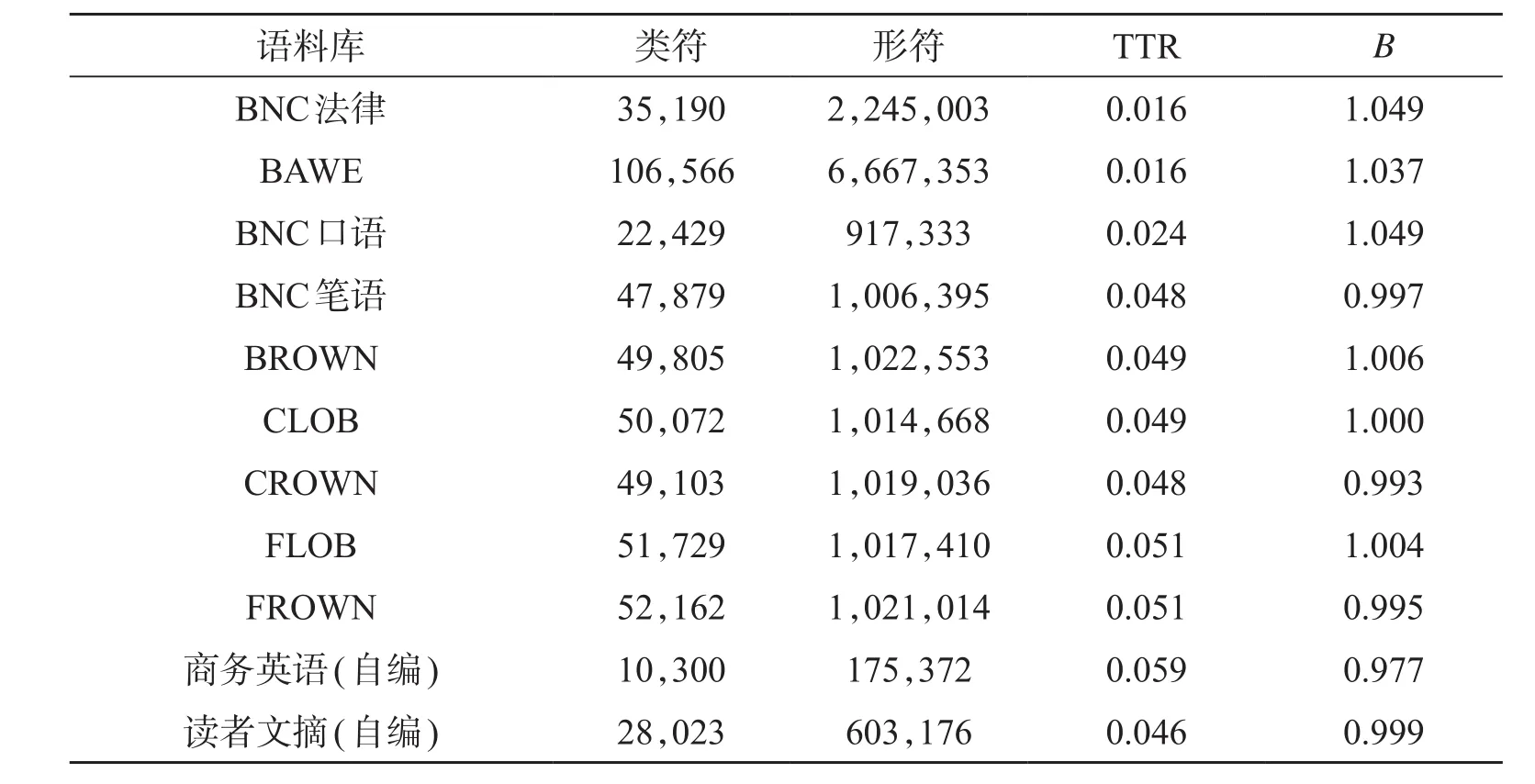
表1. 11个英文语料库的Zipf定律系数B及相关数据
基于11个英文语料库测得的一系列B数值的均值为1.01,极差为0.072。这一调查结果说明英文文本的Zipf定律系数的确近似于1,或者说用45度角下倾直线拟合英文语料库Zipf分布图像的误差不大。
一些学者曾指出,Zipf定律系数B因语言而异小幅变化,与词汇丰富度(lexical richness)或类形比有关(Gelbukh & Sidorov 2001)。所谓类形比,是类符数与形符数的比率(type-token ratio,TTR),是词汇丰富度的一个简单指标。基于表1所列数据,实施相关性分析,结果如下:
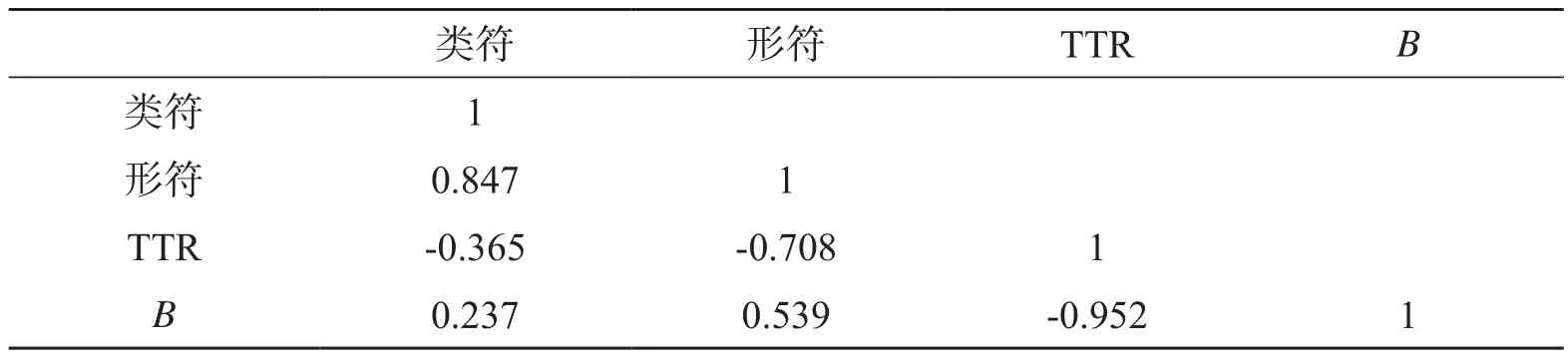
表2. 基于表1数据的相关分析
由相关分析结果可见,B与TTR间存在高度相关(r=-0.952,p<0.01),Zipf定律系数受TTR影响。既然如此,Zipf定律图像的线性倾角服从某个常数角度的趋势不存在。确凿证据再次表明序频分布并非Zipf所谓两种力量造就的词汇平衡。
综合本节中的实证研究,既然可以通过简单数学模型生成Zipf分布,其奥秘无外乎Miller(1965:vi)所谓“视语言的消息源为一个随机过程,Zipf曲线无非是该过程的必然结果”,并非最小努力的产物;既然Zipf分布的线性斜率与文本的类形比高度相关,其直线形状与线性倾角与所谓词汇平衡无关。基于上述结论足以断定Zipf定律与Zipf语言经济论的关系:后者不能解释前者,且前者并非后者的有效证据。既然如此,Zipf的语言经济论因缺乏证据而成为无本之木,产生了另一个有待探讨的问题:该如何评价Zipf的语言经济论。
4. Zipf语言经济论献疑
4.1 两种力量论之无端
Zipf的语言经济理论由统辖于最小努力原则之下的一系列假说构成,而Zipf对这些假说的论证又不乏破绽。那么,Zipf的理论是否中肯?是否能够揭示语言经济的奥秘?缜密的理性审视之下,Zipf的理论其实存在诸多破绽,其中最为致命的就是两种力量论。造就所谓词汇平衡的两种力量是否存在?按Zipf的假说,言者希望用尽可能少的工具完成尽可能多的任务,也就是希望词语的多义性强,在这个方向上存在趋于将多种意义集于一词的单一化力量;听者希望解读词汇的工作量尽可能小,也就是希望词语的多义性弱,在这个方向上存在趋向于一词仅表达一义的多样化力量。不过,这种理论捉襟见肘,与语言的规约性相悖。语言是一个规约体系,词语能表达何种、多少意义约定俗成,言者与听者势必遵循同一套规约,而自行裁定词语之意义、能指之所指的自由度很小,所以根本不可能大刀阔斧地实现两种力量。既然两种力量不可能产生实质效应,何谈平衡,何至于左右词频分布格局?由此可见,两种力量之论不仅缺乏证据,且因违背了语言的基本属性而站不住脚。
既然涉及语言的规约性,不妨从这个角度浅谈语言经济性的道理。规约性可谓语言经济性的基本要件。在这一点上语言与其他人造的或自然的通信体系一致。若言者与听者不能构成一个以共同知识为规约的通信体系,那么两者之间或根本无法沟通,或必须为传达消息付出许多额外工作。此外,规约机制为降低语言交流的开销提供了一种必要的可能性,即最少仅用一个符号、一项语言手段就可以传达一个意义实体,以至于一方面语言系统势必动用大量符号为动态变化的、潜在数量无限的主客观实体赋予称谓,而另一方面,因为人脑有处理语境制约的能力,一词多义也广泛存在,两方面均体现了语言之最小努力原则。可见,语言因规约性而省力,且为了省力,语言必然是一个规约体系。
4.2 双边经济之玄虚
两种力量无端,与两种力量相纠结的双边经济也并非顺理成章。Zipf认为言者、听者经济立场上的单边最小努力以两种力量的方式交锋,却忽视了一个不言而喻的道理:只有交流成功才有省力可言,否则必然导致额外开销,所以交流成功是达成最小努力的前提。诚然,单边最小努力的矛盾是否存在是一个真伪难断的问题,但强调这种玄虚的矛盾没有实际意义,即使有某种对立,也只能是行为方式的对立:以实现成功交流为纲,言者付出表述的工作,听者付出解读的工作,达成最小努力的方式既相反且相成。对Zipf语言经济思想有所沿革的两种著名理论,即Martinet的经济原则与Horn的R、Q原则,均明示或隐含了这个道理。
在提出R、Q原则的论文中,Horn(1984:11)开篇即引用了Zipf两种力量之说,随后又援引了Martinet的经济原则:“为了理解语言如何变化、为何变化,语言学者须谨记两个永恒相悖的因素:其一,成功交流的要求、言者对成功传达消息的要求;其二,以达成交际目标为前提,将言者生理、心理能量付出降至最低的最小努力原则”(转引自Horn 1984:11)。
对Zipf与Martinet的理论,Horn如此概括:“正如Zipf所谓‘两种对立的经济极端矛盾’,Zipf、Martinet等认为语言的变化正是在这个矛盾的熔炉中炼成的”(Horn 1984:11)。而后,Horn指出:“这两种矛盾的力量及其交互作用就是Grice会话原则以及由其所衍生的语用推理机制之主要根源”(同上:12)。Horn将Zipf的双边经济之说与Martinet的经济原则混为一谈,这分明是一个误区。Martinet将最小努力原则纳入了经济原则,也强调这是一个二元矛盾,但成功交流与最小努力的矛盾和Zipf所谓两种经济的交锋显然有本质区别,且经济原则的精髓所在就是强调成功交流是最小努力之前提。
尽管Horn将Zipf与Martinet的原则无差别概括为“两种矛盾的力量及其交互作用”,他在此基础上建构的理论并没有破绽。如下是Horn归纳的Q、R原则框架(同上:13):
1)Q原则(基于听者):充分话语量;说得尽可能多(以R为前提);下限原则,诱发上限会话含义。
2)R原则(基于言者):必要话语量;只说必须说的(以Q为前提);上限原则,诱发下限会话含义。
强调R、Q互为前提就是对成功交流是最小努力之前提这一原则的尊重。所以尽管Horn沿用了Zipf的双边经济,却没有延续其玄虚。此外,“‘基于言者’与‘基于听者’相对,‘下限’与‘上限’相对……,这是一个工整的对称”(Carston2005:305),R、Q两原则体现了言者与听者的方式相对与经济统一。Horn(2006:2)后来更新了他的理论,用“语用之阴阳互动”来描述其理论中的两种宏观对立的原则。既相反且相成,“阴阳互动”的提法显然比片面强调交锋更加合理。
5. 小结
Zipf是一位风格独特的语言学者,他视语言为一个生物、心理、社会过程,以统计、数学分析加哲学探讨的方式研究语言,进而将从语言研究中得出的哲理加以推广。Zipf的理论与计量研究中之所以不乏破绽,一方面是因为在Zipf的时代以数论理的技术条件简陋。另一方面,Zipf其人有一些值得计量、实证语言研究领域学者力戒的弱点:Zipf的数学能力有限、统计学知识不足,对数据之性质不求甚解却常在臆测理论的方向上渐行渐远(Wyllys 1981:47)。在以去伪存真的态度审视Zipf语言经济理论的同时,有两点深刻的感受:瑕不掩瑜,尽管其理论不无瑕疵,Zipf开创的理论视野博大,时至今日尚未被充分探索且仍大有可为;以Zipf为先驱的研究范式,即计量调查加推究哲理,在今天的语言研究中仍有方兴未艾之势与广阔的前景。
Carston, R. 2005. Relevance Theory, Grice and the neo-Griceans [J]. Intercultural Pragmatics 2(3): 303-319.
Gelbukh, A. & G. Sidorov. 2001. Zipf and Heaps Laws coefficients depend on Language [A]. In A.Gelbukh (ed.). Proceedings of Confenence on Intelligent Text Processing and Computational Linguistics [C]. Berlin: Springer-Verlag. 332-335.
Herdan, G. 1960. Type-Token Mathematics [M]. The Hague: Mouton.
Herdan, G. 1966. The Advanced Theory of Language as Choice and Chance [M]. Berlin: Springer.
Horn, L. 1984. Toward a new taxonomy for pragmatic inference: Q-based and R-based implicature[A]. In D. Schiffrin (ed.). Meaning, Form, and Use in Context: Linguistic Applications [C].Washington: Georgetown University Press. 11-42.
Horn, L. 2006. Speaker and hearer in Neo-Gricean pragmatics [J]. Journal of Foreign Languages(4): 2-26.
Mandelbrot, B. 1953. An informational theory of the statistical structure of languages [A]. In W.Jackson (ed.). Communication Theory [C]. Woburn, MA.: Butterworth. 486-502.
Mandelbrot, B. 1982. The Fractal Geometry of Nature [M]. San Francisco: Freeman.
Miller, G. 1957. Some effects of intermittent silence [J]. American Journal of Psychology 70(2):311-314.
Miller, G. & N. Chomsky. 1963. Finitary models of language users [A]. In R. Luce, R. Bush &E. Galanter (eds.). Handbook of Mathematical Psychology [C]. New York: John Wiley.419-492.
Miller, G. 1965. Introduction [A]. In G. Zipf (ed.). The Psycho-biology of Language: An Introduction to Dynamic Philology [C]. MA.: The MIT Press.
Thorndike, E. 1932. A Teacher’s Word Book of the Twenty Thousand Words [M]. Teachers College,Columbia University.
Wyllys, R. 1981. Empirical and theoretical bases of Zipf’s Law [J]. Library Trends 30(1): 53-64.
Zipf, G. 1945. The meaning-frequency relationship of words [J]. The Journal of General Psychology 33(2): 251-256.
Zipf, G. 1949. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology [M]. Cambridge, MA.: Addison-Wesley.
冯志伟,1983,齐普夫定律的来龙去脉 [J],《情报科学》(2):37-41。
姜望琪,2005,Zipf与省力原则 [J],《同济大学学报》(2):87-95。
通讯地址:471022 河南省洛阳市洛阳师范学院外国语学院
