随钻测量的钻进多参数模型建立
2015-08-10张奇志杨佳淼
张奇志,杨佳淼
(1.西安石油大学电子工程学院,陕西西安 710065;2.陕西省钻机控制技术重点实验室,陕西西安 710065)
建立模型就是根据实际情况,把实际系统抽象成数学模型、物理模型或者结构模型。钻进过程的复杂性决定了建立钻进过程的模型不可能像其他学科那样,采取物理的方法快速建立描述钻进过程的机理模型,最好的方法是利用钻井生产过程中记录的数据来建立描述钻进过程的数学模型。建立精确的钻进多参数模型,能够为钻进参数优化提供便利,从而确定合理的钻进参数,使钻进过程的整体经济效果达到最优的工艺技术。目前主要的钻进模型有修正的杨格模型[1]、四元钻速模型[2]、B-Y 模型[3]等,其中修正的杨格模型是在杨格模型的基础上,综合考虑钻头牙齿磨损、钻压、转速、钻井液性能以及水力因素等对钻速的影响,并结合AMOCO 研究中心和鲍格因等人的研究结果归纳建立的,该模型是根据数学、力学原理和实验而得到的经验公式,解析性较好,并且与实际钻井情况的符合率较高[4]。四元钻速模型考虑了钻压、转速、钻头比水功率和钻井液密度这4 个影响钻速的因素,该模型简单,能以较简便的方式确定各因素对钻速影响效果与可钻性级值的关系。B-Y 模型是Bourgoyne 和Young 基于前人的理论基础,从多个角度出发,把钻速模型描述为多个影响因素之间的线性组合,建立了包含8 个机械钻速影响因素的参数方程[5],该方程适用于牙轮钻头和PDC钻头,并且针对不同类型的循环介质可适当调整参数项,所有参数项都是根据所研究区域的钻井和地层数据进行回归分析得到的,更具实用性和准确性。
上述这些模型都有固定的形式,其中自变量和因变量都是确定的,这样的模型有时候不符合实际钻井情况。并且这些模型的系数难以确定,要想确定具体的模型系数,需要收集大量的完井数据,并将这些模型转换为线性模型,通过多元线性回归法求解。例如在文献[4]中,作者将B-Y 模型转换为线性模型后,收集了82组数据作为样本数据进行多元回归分析,这种方法不能够对模型系数实时修正。但是如果在新探区,面临数据量不足等一系列问题,这给要建立精确数学模型的钻井作业决策者带来很大的困难。由于钻井生产是一个随时变化的动态过程,其数学模型是随时间变化的,这就需要一种实时建模方法,以实现钻进过程的实时动态模拟[6]。
1 多元线性模型建模方法
多元回归建模方法,如逐步回归法和最小二乘法等,其计算方法太繁琐,难以满足实时建模的需要。下面将介绍一种简便,能满足实时建模需要的多元线性模型建模方法:自适应跟踪法[7]。该方法的主要思路是用当前时刻系数的预测值以及实际值来修正下一时刻的系数,具体步骤如下。设钻井模型为:







再用第(r+2)次采样值,求得y 的(r+2)次预报值:

按照上述步骤计算,直到算出un后,求得y 的(r+n)次预报值,取满足方程的,计算un+1=un+以上每步出现的方程组都有解,否则可以考虑最小二乘解等。
2 模型准确性分析
在上述递推修正算式中:

由上式看出un+1是历次实测值,…及初始动态参数u0的加权平均值,其权重分别为M,M(I-M),…M(I-M)n,(I-M)n+1,权重依次减少,表明对近期采样数据的重视,当n 较大时,权重之和为1,un+1是使:

取值最小的u。
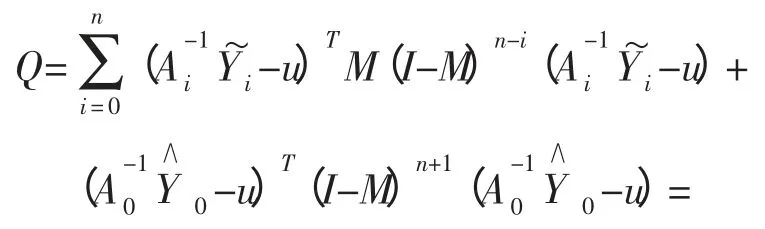
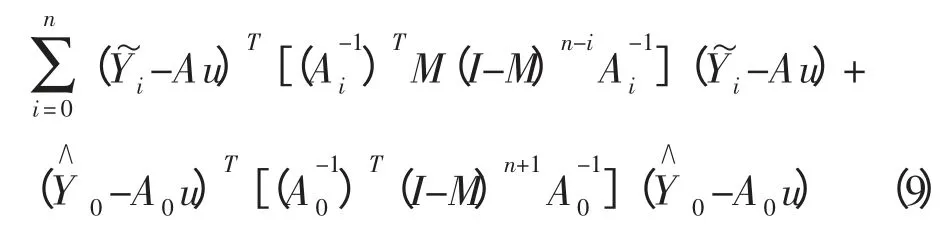
当n 无穷大时,式(9)第二项趋于零,所以认为un+1使式(9)第一项和最小,此外这一项正是用最小二乘法求回归方程~Y=Au 中回归系数向量u 的加权和。un+1正是用采样值(A0,Y0),(A1,Y1),…(An,Yn)来确定的回归系数向量。这就是n 越来越大时,由=An+1u来预测越来越准的原因,此时模型也更加精确。
3 实例分析
为了验证上述方法的正确性,本文利用钻井现场收集到的实时数据,用SPSS 统计软件和上述方法建立模型。在某钻井作业中,以10 min 为一个周期进行数据采样,收集了15 组数据,数据包括钻速V,钻压W,转速n,比水功率Eb,用来建立钻速依赖于钻压、转速、比水功率的数学模型(见表1)。
方法一:用SPSS 统计分析软件对数据进行多元线性回归分析[9,10],得到多元线性回归系数结果(见表2)。

表1 钻井数据表

表2 多元线性回归系数结果表
各项系数对应的Sig 值均小于显著性水平α=0.05,所以钻速与钻压、转速和比水功率有显著性关系。

方法二:根据表中数据,取初始模型为:

则u0=(2.5,0,0,0)T,取M=αI,α=0.618,I 为4×4单位矩阵。

得矩阵:

得:


仿照上述步骤依次求解,结果(见表3)。此时预测值u7=(1.776 8,0.002 0,0.006 6,0.101 2)T,第11 组数据预测值=2.486,误差为-=0.006,这时的系数与用SPSS 软件建立的回归方程系数相当接近,并且预测误差也很小。
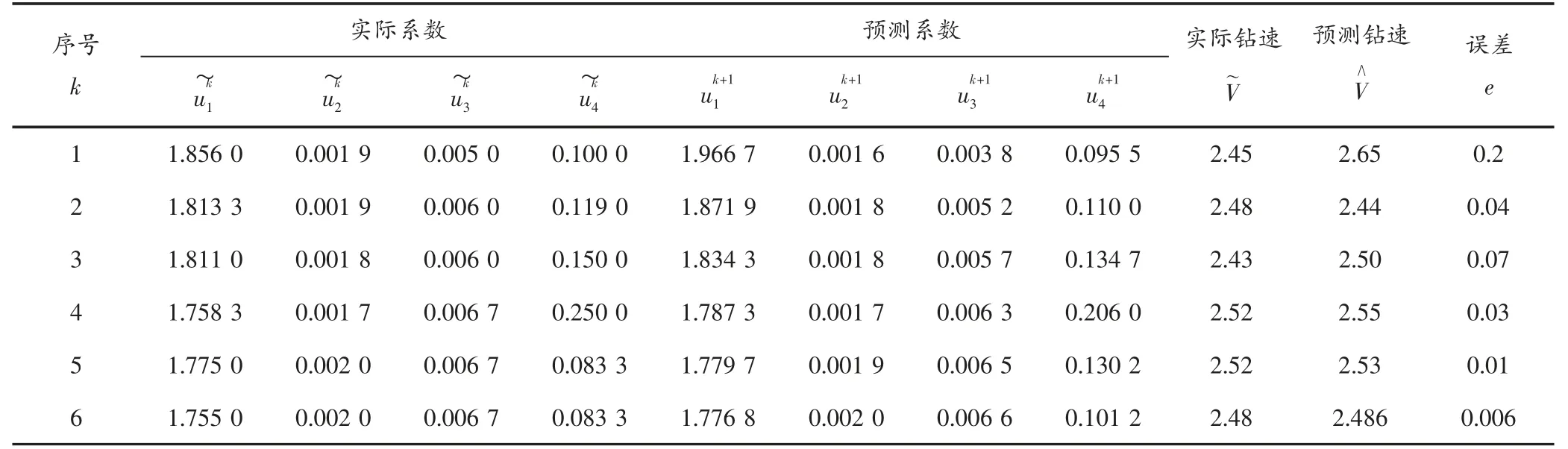
表3 系数求取结果表
这个例子说明,用多参数模型自适应跟踪法可在没有完井数据和合适模型的情况下,利用现场实测数据,能够快速的跟踪出一个多参数的钻进模型,并能够对模型系数进行实时修正,这给在新井需要建立钻进模型的钻井工作者带来很大的便利。
4 结论
(1)利用自适应跟踪法,可以在没有完井数据和合适钻井模型的情况下,快速的建立一个精确的数学模型,并且可以随时间的推移和样本的扩大而自行修正模型中的系数[11],使其更符合钻井生产实际。
(2)快速的实时建立数学模型,并且对模型中的系数实时修正,为钻进多参数实时优化提供了便利[12]。
(3)为了使模型更符合钻井实际,模型中应加入更多影响钻进的因素,这时应该编写相应的程序来完成模型的建立。
[1] Warren TM.Drilling model for soft formation bit[J].Journal of Petroleum Technology,1981,33(6):7-9.
[2] 张立刚.岩石可钻性综合预测与应用研究[D].大庆:大庆石油学院,2008.
[3] 范成洲,尹晓利,曹钧,等.大直径竖井钻井钻速多元回归模型分析及应用[J].矿山机械,2012,40(5):16-20.
[4] Florence F,Iversen F P.Real-time models for drilling process automation:equations and applications[C].IADC.SPE Drilling Conference and Exhibition.Society of Petroleum Engineers,2010.
[5] Chandan Guria,Kiran K Goli,Akhilendra K Pathak.Multiobjective optimization of oil well drilling using elitist nondominated sorting genetic algorithm[J].Petroleum Science,2014,11(1):97-110.
[6] 张卫东,刘晓晓,王勇,李忠庆.电子钻井实时模拟系统[J].中外能源,2008,13(4):39-42.
[7] 唐娴,戴经梁,贾倩.参数自适应跟踪法预测高速公路路面使用性能[J].长安大学学报,2007,27(3):31-33.
[8] 于润桥.钻进过程影响因素的计算机仿真[J].石油钻探技术,1996,24(3):7-10.
[9] 李昌盛.基于多元回归分析的钻速预测方法研究[J].科学技术与工程,2013,13(7):1740-1744.
[10] 郭勇,陈跃,徐勇,苏宏岸.钻井液参数设计加权回归分析模型的研究[J].科技创新与应用,2015,(3):21-22.
[11] 党胜,等.基于自适应跟踪法的路面使用性能研究[J].公路交通科技,2007,(9):43-44.
[12] 李士斌,张立刚,荆玲,徐守锋.钻井参数优选新方法[J].石油钻探技术,2007,35(4):9-11.
