地震数据广义合成的频率空间域逆时偏移

陈国新，陈生昌，任浩然，王汉闯，周华敏

（浙江大学 地球科学系，浙江 杭州，310027）

逆时偏移最早由Whitmore［1］在1982 年第53届地球物理勘探工作者学会（society of exploration geophysicists，SEG）上提出，相对于单程波偏移、Kirchhoff偏移，在解决多路径、大倾角、多次波和保幅等重要问题上具有不可比拟的优势，所以得到了广泛的研究与关注.目前困扰逆时偏移应用到实际数据处理的瓶颈是巨大的计算与存储量，以及低频噪音的干扰.其中逆时偏移巨大的计算量与炮道集个数有关，炮道集个数越多则计算效率就越低，另外边界反射的处理也会增加逆时偏移计算量.

在保证成像质量的前提下减少炮道集数可以提高逆时偏移计算效率.Berkhout［2］提出的面炮偏移技术，把震源和记录进行线性叠加，然后利用合成数据进行偏移成像，相对于常规的单炮偏移方法显著的降低了计算量，实质上是一种基于平面波合成的偏移方法.很多学者从不同的角度对平面波做了大量的研究工作，张叔伦等［3］利用傅里叶有限差分延拓算子，提高了平面波偏移的计算精度，陈生昌等［4］证明了共炮点与共偏移距平面波偏移的等价性，韩利等［5-6］实现了VTI、TTI介质隐式有限差分平面波偏移，叶月明等［7］将平面波偏移应用到起伏地表资料中.类似于平面波偏移，改变地震数据的线性叠加方式则可得到不同的偏移方法，例如对炮集与道集记录进行随机延迟叠加就可以得到随机合成数据偏移方法［8］.陈生昌等［9］根据地震波场的线性叠加理论和地震数据采集过程中地下响应的时不变特性，将地震数据的共炮道集平面波合成、控制照明、相位编码与小波束偏移中的局部道集合成归结到统一的道集数据线性合成框架下，提出了对地震数据及其震源进行线性叠加的一般性方案，即地震数据广义合成方法.

逆时偏移在时间域，频率域均可实现，频率域相对于时间域具有计算高效，数据选择灵活，易于构造PML边界条件，不存在时间频散和累积误差的优势［10-12］.Jo等［13］提出的旋转坐标系的九点差分格式以及Shin等［14-16］在此基础上推广得到的更精确的差分格式，解决了频率域的正演计算问题.频率域正演算法的计算量集中在求解一个规模巨大的带状方程组上，任浩然等［17］利用矩阵压缩存储技术大幅度减少了算法的计算与存储量，降低了算法对数据规模大小的限制.Loewenthal等［18］最早实现了频率空间域的逆时偏移，Mulder等［19-20］］提出了频率空间域保幅偏移以及计算频率的选择方法，Kim 等［21］则给出了频率空间域逆时偏移中的震源子波估计算法，Ren 等［22］在频率空间域实现了最小二乘偏移.

本文在地震数据广义合成理论基础上，利用合成数据实现了频率空间域基于地震数据广义合成的逆时偏移，将逆时偏移计算效率提高到了1.5～3倍，引入了PML边界条件消除边界反射，利用带有振幅与频率补偿的拉普拉斯滤波方法消除了偏移结果中的低频噪音.通过对简单的二维凹陷模型以及Marmousi模型进行模拟试验，证明了本文方法的正确与高效性.

1 方法原理

1.1 地震数据广义合成

共炮点道集数据与野外采集数据一致，符合波场传播的物理过程，是当前地震数据叠前深度偏移成像中最为常用的一种数据道集.当满足对于不同时间激发的震源地下系统有相同的响应函数这一条件时，共炮点道集的波场满足线性叠加原理.

对于一个二维数据道集，设深度为z的观测面上存在频率域共炮道集波场数据u（sx，gx，z，ω），sx为炮点坐标，gx为检波器坐标，ω 为频率，根据陈生昌提出的地震数据广义合成理论，地震记录广义合成可以表示为以下线性积分：

式中：k（ξx，sx，z；ω） 为地震数据广义合成的核函数，（ξx，gx，z；ω） 为共炮点地震记录的广义合成地震记录.若与各个共炮点道集所对应的震源波场具有相同的频谱特性S（ω） ，则深度z 上的震源波场可表示为

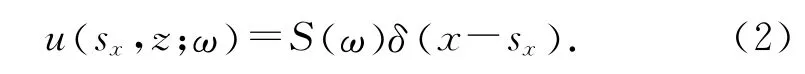
利用相同的核函数k（ ξx，sx，z；ω） ，同理可得到地震震源的广义合成（ξx，sx，z；ω）

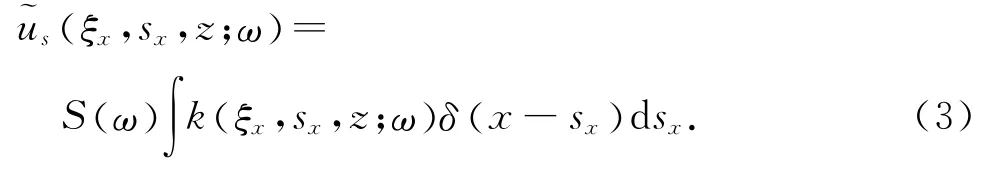
广义合成道集与震源是将多个共炮点道集地震记录数据与地震震源分别进行线性叠加而得到合成地震记录与合成震源，而叠加的方式由核函数来决定.不同的核函数对应着不同的线性叠加方法，也就得到不同的广义合成数据.具体而言，当

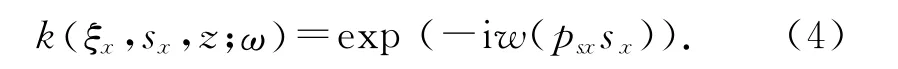
则式（1） 、（3） 就是平面波数据合成，其中psx为x 方向的平面波参数，不同的平面波参数对应着不同的平面波数据道集.当

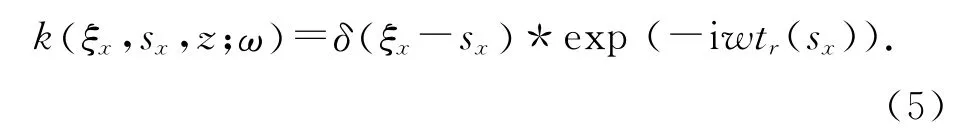
式中：tr（sx）为 炮 点位 置 上 的 时 间 随机 函 数，则式（1），（3）就是共炮点道集地震数据与震源经随机合成得到的随机合成道集与随机合成震源.当然，除了上述2种线性叠加方法，核函数还有其他很多种取法，如当核函数取为高斯窗口函数与平面波函数的乘积就可得到束地震数据合成.

1.2 地震数据广义合成的频率空间域逆时偏移

1.2.1 频率空间域有限差分数值模拟 根据线性叠加原理，基于广义合成数据的逆时偏移与常规的共炮道集逆时偏移相同，利用正演算子正向外推广义合成震源数据得到正演波场，然后将广义合成道集数据反向传播，应用互相关成像条件得到偏移结果.所以要得到一个好的偏移结果首先要解决好波场的传播问题.波场传播既可以放在时间空间域，也可以在频率空间域进行.相对于前者，后者不涉及时间差分近似所以不存在时间频散问题，可以灵活地选择计算频带并且不同频率的系数矩阵相对独立，便于实现多频率并行运算以便提高计算效率.

频率域的二维声波方程可写为

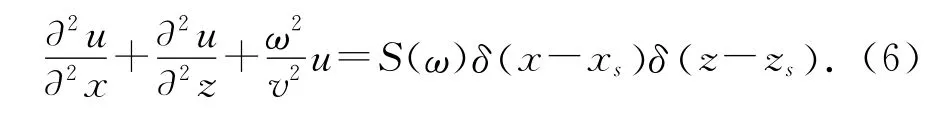
式中：u （x ，z，ω） 为频率域波 场 值，v （x ，z） 为 介 质 中声波传播速度，xs，zs是震源在观测系统中的坐标位置.求解方程（6）一般采用有限元或有限差分法.Pratt等［23］最早提出了二阶差分离散方法，即5 点差分格式，精度较差，每个波长需要13个网格点才能将相速度误差控制在1%以内，Jo通过结合45°旋转坐标系和质量加速项优化提出了优化9点差分格式，每个波长只需要4个网格就可以使相速度误差控制在1%以内，随后Jo的思想被广泛推广，从优化9点差分格式发展到优化25点差分格式，计算精度有了进一步的提高，每个波长网格数可以下降到2.5，但是相应的矩阵存储要求也随即增大，权衡计算精度与算法存储，本文采用Jo的优化9点差分格式求解方程（6）.

消除边界反射是波场正演模拟中一个重要的问题.由Berenger［24］提出 的PML 边界条件的吸收效果要好于旁轴近似与海绵吸收边界条件，而且在频率域构造带PML 边界条件的波动方程也十分方便，二维频率域带PML 边界条件的声波波动方程可写为

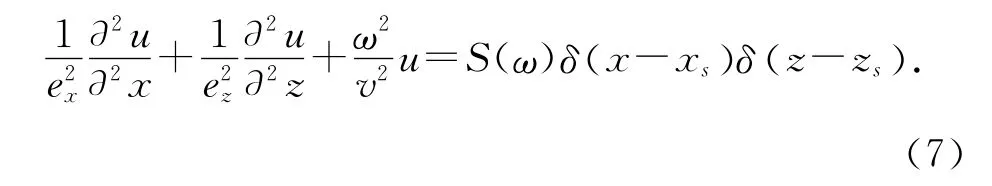
式中：ex，ez为边界衰减函数，以ex为例，ex＝1-d （x） ，其中 d （x） 为衰减因子，则

式中：a0为一常数，一般取经验值1.79，f0为震源主频，Lp为PML边界厚度，xi为PML边界条件内某点与内层边界的x 方向距离.

利用Jo的优化9点差分格式，则式（7）可写为波动方程的矩阵表达式：

若波场模拟空间大小为Nx×Nz＝N，则A （v ，ω） 是大小为N×N，与模型的物性参数，所选用的差分格式以及边界条件相关的阻抗矩阵.U（ω） 是某个频率下模型空间中所有网格点上的频率域波场值构成的N×1的列向量，S（ω） 则是在频率域中震源所构成的N×1的列向量.对于地震数据广义合成偏移，只需要分别将S（ω） 取值为广义合成震源数据和广义合成道集数据，然后求解方程（9）就可以分别得到频率空间域的正演波场值以及反向传播波场值.

方程（9）主要有2种求解方法：因式矩阵LU 分解直接解法与迭代法.迭代法对计算机存储要求较低，但其不便于并行运算，而且需要预处理以保证算法的收敛性.制约直接解法应用的是大型矩阵A （v ，ω） 的LU 分 解，直 接 对 矩 阵A （v ，ω） 进 行 分 解需要相当大的计算量与存储空间，而利用稀疏对称矩阵的压缩存储技术，可以将矩阵A （v ，ω） 压缩存储成N×9大小，分解得到的L、U 矩阵压缩为N×（2 ＋Nx）大小.这样不仅减少了算法所需要的存储空间，并且减少了因式矩阵的带宽，而因式矩阵带宽直接关系着因式矩阵LU 分解计算量的大小，从而显著的提高了计算效率.直接求解法的绝大部分计算量分布在对矩阵A （v ，ω） 的LU 分解上，完成LU分解后，对频率ω 进行并行运算，重复利用L、U 矩阵，则只需要增加很少的计算量就可以完成波场的正向与反向传播，使得算法具有很高的计算效率.

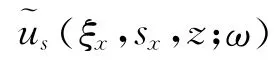
式中：ℜ表示取实部，＊表示复共轭运算，Nω表示计算的频率总个数.

低频噪音是除了计算与存储之外另一个制约逆时偏移广泛应用的问题.低频噪音产生的机制在于根据互相关成像条件，空间中凡是满足成像条件的位置都可成像，而逆时偏移采用双程波波动方程，震源波场和检波波场在传播过程中若遇到强波阻抗界面则会产生背向反射，这些背向反射的震源波场与检波波场参与到成像中会导致成像结果中出现传播方向相反的波前面的互相关结果，其对应的波矢量的夹角很大，接近或等于180°，是没有物理意义的成像结果，集中表现为低频噪音［25］.

根据低频噪音的产生机制，目前消除低频噪音的方法主要分为3大类：1）波场传播过程中去噪；2）应用成像条件去噪；3）成像后滤波法去噪.前2种去噪方法要么需要增加额外的计算量，要么应用范围具有很大的局限性，而成像后滤波去噪法不需要改变波动方程与成像条件，只是对成像结果进行滤波处理，简单易行而且应用范围广.这类方法主要包括高通滤波，导数滤波与拉普拉斯滤波方法.高通滤波简单易行但是无法彻底消除低频噪音，而且还会破坏波场的低频信息，导数滤波会改变波场相位，引入高频噪音.拉普拉斯滤波就是直接将拉普拉斯算子作用在成像结果I （x ，z） 上，即

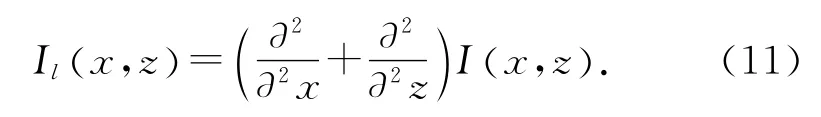
式中：Il（x ，z） 为I （x ，z） 经过 拉 普 拉 斯 滤 波 之 后 得到的成像结果.张宇等［26］给出了拉普拉斯滤波更直观的物理意义，在波数域拉普拉斯算子有以下的等价形式：

对偏移结果做拉普拉斯滤波就相当用cos2θ对成像剖面进行角度衰减，衰减掉震源波场与检波波场波矢量夹角为超大角度时两者互相关得到的成像结果，从而消除低频噪音.但是若对成像结果直接做拉普拉斯滤波，式（12）右端项中的4／v2与-ω2分别会对偏移剖面振幅与频率成分产生影响.在频率空间域做逆时偏移很容易消除这些影响，即在对所有单个频率的偏移结果做叠加之前先对偏移成像结果进行-1／ω2的频率补偿，再进行叠加求和，然后对叠加结果进行拉普拉斯滤波，完成滤波之后将偏移结果乘上v2／4做振幅补偿.加入振幅与频率补偿后的拉普拉斯滤波可以很好地去除偏移剖面低频噪音，而且保证了偏移结果幅值的正确性，数值试验结果也对该方法的实用效果进行了验证.

基于地震数据广义合成的逆时偏移方法除了低频噪音，还存在不匹配的震源波场与道集波场相互作用产生的交叉噪音（Cross-talk），要消除交叉噪音除了选择好的广义合成函数，最简单有效的方法就是增加广义合成数据的个数，然后将不同的合成数据偏移结果进行叠加以压制交叉噪音.对于平面波偏移，Liu等［27］证明了当平面波个数达到一定数量时平面波偏移可以达到常规偏移结果的效果，而张宇等［28］则给出了使平面波偏移达到常规炮偏移结果效果的最小平面波个数的计算公式：

式中：Ns为共检波点道集的炮数，Δxs为炮间距，NsΔxs对应的是共检波点道集长度，f＝w／2π，α1，α2为入射角，vs为地表速度.从式（13）可以看出，如果地震数据的频率较低时不需要太多的平面波，而根据速度模型中速度变化情况调节入射角范围也可降低平面波个数，例如当地下介质速度随深度变化剧烈时入射角不宜过大，因为入射角过大的平面波在传播过程中更易发生全反射而使波无法达到预定深度.对于随机合成数据逆时偏移，Godwin等［29］指出增加合成数据个数同样可以压制交叉噪音，但是不同于平面波偏移，由于随机合成数据的随机性导致增加数据合成个数无法完全消除交叉噪音.广义合成数据个数的增加会导致计算量的增加，所以最终的合成数据量要在计算量与成像质量之间做权衡.

2 数值试验

为了验证广义合成数据在频率空间域的逆时偏移效果，用一个凹陷速度模型进行检验.模型网格大小为100×100，纵横网格间距均为5m，地表放炮共100炮，炮间距5m，道间距5m，第一炮位于坐标原点，利用主频为30 Hz的雷克子波，地表全孔径接收.时间采样间隔为1ms，采样点数为800.速度模型如图1（a）所示，3层速度分别为2 000、3 000和4 500m／s.

在此速度模型上分别进行常规共炮点道集频率空间域逆时偏移，平面波逆时偏移和随机合成数据逆时偏移，PML 边界条件的吸收衰减层厚度为30个网格点，计算频率范围为5～35 Hz，其中平面波与随机合成数据个数均为11个（其中平面波参数为

并利用带有振幅和频率补偿的拉普拉斯滤波处理低频噪音，偏移结果分别为图1（b），（c），（d）所示.从计算效率上来讲，常规共炮点道集偏移方法需要计算100个单炮偏移结果然后叠加，利用频率并行运算，总计算时间为246.3s.而利用广义数据合成偏移方法只需要11个合成数据，数据合成用时8.9s，偏移计算用时61.9s，总计算时间是常规炮偏移方法的28.7%，计算效率提高了将近3倍.比较图（b）与（c）可以发现利用平面波进行偏移不仅计算效率高，而且在强反射界面处如凹陷底部的噪音甚至要比常规共炮点逆时偏移方法更少，这是因为平面波偏移不存在常规偏移方法偏移孔径的问题.而随机合成偏移方法也可以得到与常规偏移方法基本等效的成像结果，只是该偏移方法成像结果中的交叉噪音具有随机性，单纯增加合成数据个数也无法完全压制掉，偏移效果要稍差于平面波逆时偏移.

图1 凹陷模型数值试验Fig.1 Numerical experiments on Sag velocity model

为了进一步检验频率空间域中广义合成数据的偏移效果，本文将该算法应用到Marmousi速度模型，该速度模型非常复杂，其地质背景是安哥拉Quenguela地槽的一个剖面.截取速度模型一部分并对速度模型进行5m×5m 的网格重采样，模型网格大小为240×250，共240 炮，第1 炮点位置位于坐标原点.如图2所示为重采样后的速度模型.利用PML边界条件，边界厚度为30 个网格点，计算频率为5～45 Hz.利用频率并行运算，常规共炮点道集偏移总计算时间为2 391.6s.平面波与随机合成数据个数均为31（pmin＝-1.5×10-4s／m ，pmax＝1.5×10-4s／m，dp＝10-5s／m ），数 据 合 成 时 间89.1s偏移计算时间为840.7s，总计算时间为常规偏移方法的38.8%，计算效率提高了1.5 倍.对应的偏移结果分别为如图3、4、5所示，比较图3与4，虽然平面波偏移的炮道集数只有常规共炮点道集偏移方法的1／8，但是偏移结果与常规偏移结果基本一致，不仅清晰正确地显示出了强反射界面，对于细微的速度变化区域也有很好的勾勒.相比较常规偏移与平面波偏移，随机合成数据偏移效果相对较差，尤其是在浅层因为覆盖次数较少，随机交叉噪音没有得到很好的压制，但是成像结果也可以达到实用的要求.为了更清楚的对比3种方法得到的偏移效果，特别的抽取3个偏移结果中的第100道数据进行对比（见图6）.从单道的波形图上可以看出，平面偏移结果与常规炮偏移结果不论是在波形上还是在振幅上都能够很好的一一对应，显示出了平面波偏移方法的高效与准确.随机时间合成数据偏移结果除了表层的波形存在畸变外（图6（C）圆圈标记区域），其他区域振幅与波形也能够与前2个偏移结果很好的对应.而且在处理实际生产中的数据时，浅层的交叉噪音会被数据自身所带的噪音所掩盖.

3 结 语

地震数据广义合成及其逆时偏移成像是平面波偏移，随机合成数据偏移等基于线性叠加原理减少炮道集数的偏移方法在数学上的抽象与推广.改变合成函数的形式可以得到基于不同线性叠加方法的合成数据，使得发展出更高效准确、更具针对性的波动方程叠前逆时偏移成为可能.综合利用地震数据广义合成与频率空间域的计算优势将逆时偏移的计算效率提高了1.5～3倍，通过引入PML边界条件与带有振幅和频率补偿的拉普拉斯滤波方法使得偏移结果质量得到了很好的保证，能够达到与常规频率空间域逆时偏移基本等效的成像效果.其中平面波数据逆时偏移不存在随机合成数据逆时偏移中的随机交叉噪音，成像效果更好.

图2 重采样后的Marmousi速度模型Fig.2 Marmousi velocity model after resampling

图3 常规共炮点道集逆时偏移方法的偏移结果Fig.3 Result of conventional common-source gathers reverse-time migration

图4 平面波逆时偏移结果Fig.4 Result of plane-wave reverse-time migration

图5 随机合成数据逆时偏移结果Fig.5 Result of random synthetic reverse-time migration

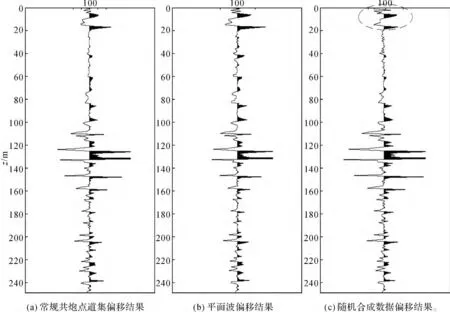
图6 不同偏移方法得到的偏移结果的第100道波形图对比Fig.6 Comparison of 100th channel’s amplitude of different migration results

针对不同地震数据特征发展更好的合成函数是进一步提高逆时偏移计算效率和偏移成像质量的有效途径.另外目前频率空间域的正演方法还缺乏高效的高阶差分格式，要保证计算精度则模拟网格间距不能太大，限制了频率空间域逆时偏移的应用范围，所以发展具有较高计算效率的高阶频率空间域有限差分算法也是未来一个重要的研究方向.

（

）：

［1］WHITMORE N D.Iterative depth imaging by backward time propagation ［C］∥53th Annual International SEG Meeting，Expanded Abstracts.Las Vegas：SOC Exploration Geophysicists，1983：382-384.

［2］BERKHOUT A J.Areal shot-record technology［J］.Journal of Seismic Exploration，1992，1（2）：25l-264.

［3］张叔伦，孙沛勇.基于平面波合成的傅里叶有限差分叠前深度偏移［J］.石油地球物理勘探，1999，34（1）：1-7.ZHANG Shu-Lun，SUN Pei-Yong.Fourier finite-difference prestack depth migration based on plane wave synthesis［J］.Petroleum Geophysical Prospecting，1999，34（1）：1-7.

［4］陈生昌，曹景忠，马在田.叠前数据的平面波深度偏移方法［J］.地球物理学报，2003，46（6）：1176-1185.CHEN Sheng-chang，CAO Jing-zhong，MA Zai-tian.A plane wave depth migration method for pre-stack seismic data［J］.Chinese Journal of Geophysics，2003，46（6）：1176-1185.

［5］韩利，韩立国，崔 杰，等.VTI介质隐式有限差分平面波偏移［J］.物探化探计算技术，2011，33（2）：115-121.HAN Li，HAN Li-Guo，CUI Jie，et al.Implicit finitedifference plane wave migration in VTl media［J］.Computing Techniques For Geophysical And Geochemical Exploration，2011，33（2）：115-121.

［6］韩利，韩立国，巩向博，等.TTI介质隐式有限差分平面波偏移［J］.地球物理学报，2011，54（4）：1090～1097.HAN Li，HAN Li-Guo，GONG Xiang-Bo，et a1.Implicit finite-difference plane wave migration in TTI media［J］.Chinese Journal of Geophysics，2011，54（4）：1090-1097.

［7］叶月明，李振春，仝兆岐，等.起伏地表条件下的合成平面波偏移及其并行实现.石油地球物理勘探［J］.2007，42（6）：622-628.YE Yue-ming，LI Zhen-chun，TONG Zhao-qi，et al.Synthetical plane wave migration and parallel realization in the condition of rugged surface［J］.Oil Geophysical Prospecting，2007，42（6）：622-628.

［8］陈生昌，王汉闯，佘德平.地震数据广义随机合成的偏移成像.石油地球物理勘探［J］.2012，47（6）：868-872.CHEN Sheng-chang， WANG Han-chuang，SHE Deping.Generalized random synthetic of seismic data and its migration［J］.Oil Geophysical Prospecting，2012，47（6）：868-872.

［9］陈生昌，马在田.广义地震数据合成及其偏移成像［J］.地球物理学报，2006，49（4）：1144-1149.CHEN Sheng-chang，MA Zai-tian.Gernerlized synthesis of seismic data and its migration［J］.Chinese Journal of Geophysics，2006，49（4）：1144-1149.

［10］PRATT R G.Frequency-domain elastic wave modeling by finite differences：A tool for crosshole seismic imaging［J］.Geophysics，1990，55（5）：626-632.

［11］STEK I，PRATT R G.Accurate viscoelastic modeling by frequency-domain nite differences using rotated operators［J］.Geophysics，1998，63（5）：1779-1794.

［12］殷文，印兴耀，吴国忱，等.高精度频率域弹性波方程有限差分方法及波场模拟［J］.地球物理学报，2006，49（2）：561-568.YIN Wen，YIN Xing-yao，WU Guo-chen，et al.The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation［J］.Chinese Journal of Geophysics，2006，49（2）：561-568.

［13］JO C H，SHIN C，SUH J H.An optimal 9-point，finite-difference，frequency-space，2-D scalar wave extrapolator［J］.Geophysics，1996，61（2）：529-537.

［14］SHIN C，SOHN H.A frequency-space 2-D scalar wave extrapolator using extended 25-point finite difference operators［J］.Geophysics，1998，63（1）：289-296.

［15］曹书红，陈景波.声波方程频率域高精度正演的17点格式及数值实现［J］.地球物理学报，2012，55（10）：3440-3449.CAO Shu-hong，CHEN Jing-bo.A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation［J］.Chinese Journal of Geophysics，2012，55（10）：3440-3449.

［16］刘璐，刘洪，刘红伟.优化15 点频率-空间域有限差分正演模拟［J］.地球物理学报，2013，56（2）：644-652.LIU Lu，LIU Hong，LIU Hong-wei.Optimal 15-point finite difference forward modeling in frequency-space domain［J］.Chinese Journal of Geophysics，2013，56（2）：644-652.

［17］任浩然，王华忠，龚婷.标量地震波频率-空间域有限差分法数值模拟［J］.石油物探，2009，48（1）：20-26.REN Hao-ran，WANG Hua-zhong，GONG Ting.Seismic modeling of scalar seismic wave propagation with finitedifference scheme in frequency-space domain［J］.Geophysical Prospecting For Petroleum，2009，48（1）：20-26.

［18］LOEWENTHAL D，MUFTI I R.Reverse time migration in spatial frequency domain［J］.Geophysics，1983，48（5）：627-635.

［19］PLESSIX R E，MULDER W A.Frequency-domain nitedifference amplitude-preserving migration［J］.Geophysical Journal International，2004，157（3）：975-987.

［20］MULDER W A，PLESSIX R E.How to choose a subset of frequencies in frequency-domain finite-difference migration［J］.Geophysical Journal International，2004，158（3）：801-812.

［21］KIM Y，MIN D J，SHIN C.Frequency-domain reversetime migration with source estimation［J］.Geophysics，2011，76（2）：41-49.

［22］REN H R，WANG H Z，CHEN S C.Least-squares reverse time migration in frequency domain using the adjoint-state method［J］.Journal Of Geophysics And Engineering，2013，10（3）：035002.

［23］PRATT R G，WORTHINGTON M H.Inverse theory applied to multi-source cross-hole tomography part1：Acoustic wave equation method［J］.Geophysical Prospecting，1990，38（3）：287-310.

［24］BERENGER J P.A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of computational Physics，1994，114：185-200.

［25］杜启振，朱钇同，张明强，等.叠前逆时深度偏移低频噪声压制策略研究［J］.地球物理学报，2013，56（7）：2391-2401.DU Qi-zhen，ZHU Yi-tong，ZHANG Ming-qiang，et al.A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration［J］Chinese Journal of Geophysics，2013，56（7）：2391-2401.

［26］ZHANG Y，SUN J.Practical issues of reverse time migration：True amplitude gathers，noise removal and harmonic-source encoding ［C］∥70th EAGE International Annual Meeting，Extended Abstracts.Rome：European Association of Geoscientists ＆Engineers，2008：29-35.

［27］LIU F Q，HANSON D W，WHITMORE N D，et al.Toward a unied analysis for source plane-wave migration［J］.Geophysics，71（4）：129-139.

［28］ZHANG Y，SUN J，GRAY S，et al.Sampling issues in delayed-shot migration and Plane-wave migration［C］∥68th EAGE Annual Conferenc and Exhibition，Expanded Abstacts.Vienna：European Associaion of Geoscientists＆Engineers，2006：1-4.

［29］GODWIN J，SAVA P.A comparison of shot-encoding shemes for wave-equation migration［J］.Geophysica Prospecting，2013，61（1）：391-408.