Robust Dataset Classi fi cation Approach Based on Neighbor Searching and Kernel Fuzzy C-Means

Li Liu,Aolei Yang,Wenju Zhou,Xiaofeng Zhang,Minrui Fei,and Xiaowei Tu

Robust Dataset Classi fi cation Approach Based on Neighbor Searching and Kernel Fuzzy C-Means

Li Liu,Aolei Yang,Wenju Zhou,Xiaofeng Zhang,Minrui Fei,and Xiaowei Tu

—Dataset classi fi cation is an essential fundament of computational intelligence in cyber-physical systems(CPS).Due to the complexity of CPS dataset classi fi cation and the uncertainty of clustering number,this paper focuses on clarifying the dynamic behavior of acceleration dataset which is achieved from micro electro mechanical systems(MEMS)and complex image segmentation.To reduce the impact of parameters uncertainties with dataset classi fi cation,a novel robust dataset classi fi cation approach is proposed based on neighbor searching and kernel fuzzy c-means(NSKFCM)methods.Some optimized strategies, including neighbor searching,controlling clustering shape and adaptive distance kernel function,are employed to solve the issues of number of clusters,the stability and consistency of classi fi cation,respectively.Numerical experiments fi nally demonstrate the feasibility and robustness of the proposed method.

Index Terms—Dataset classi fi cation,neighbor searching,variable weight,kernel fuzzy c-means,robustness estimation.

I.INTRODUCTION

IN applications of cyber-physical systems(CPS),the dataset classi fi cation is the essential fundament of computational intelligence.The dataset in general can be achieved from sensors,images,videos and audio fi les.The clustering is an unsupervised learning process for dataset classi fi cation,which makes a cluster including more similar data than that of other clusters.The unsupervised learning as a main algorithm in the classi fi cation can be applied to image segmentation,pattern recognition,data mining and bioinformatics.

For the dataset classi fi cation,fuzzy clustering methods are divided into hard c-means(HCA)[1]and fuzzy c-means (FCM)[2]in the unsupervised learning.In contrast to the HCA,the FCM has better performance on the signi fi cantdata presentation and clustering effect.Based on it,Wu et al.proposed a new metric which is called alternative hard c-means(AHCM)and alternative fuzzy c-means(AFCM) clustering algorithms[3].The two algorithms actually modify the distance function,but the clustering result is fuzzy,because the value is less than 1 during iteration.Ahmed et al.presented a bias corrected FCM(BCFCM)algorithm[4].This method introduces a spatial term of immediate neighborhood which allows a point to be in fl uenced by the labels.Its weakness is high time consumption in the iteration.In addition,Chen et al.investigated a preprocessing image smoothing step based on the BCFCM,but it cannot control the trade-off between smoothing and clustering[5].Szilagyi et al.presented an enhanced FCM(EnFCM)algorithm using biases to solve the piecewise homogeneous labeling problem[6].Although the relevant classi fi cation is effective,it fails in the piecewise partition according to the label interval.A semi-supervised FCM(SS-FCM)algorithm was introduced by Li et al.[7], which provided a new iterative procedure to calculate the membership labeled and unlabeled samples with the drawback of the complex calculation.It is noted that the above mentioned FCM clustering methods fail to computer the nonrobust Euclidean distance,and cannot reject noises which are inconvenient in practical applications.

Although FCM has been successfully applied in many fi elds,it is unable to select the fuzzy weighting exponent and to determine the priori knowledge of the cluster prototype. An example for an approach is hierarchical multi-relational clustering algorithm[8],which is adopted to solve one-to-many relationship of dataset classi fi cation.The order production scheduling method has been employed based on the subspace clustering mixed model(SCMM)[9],and the kernel method was a feasible direction for the dataset classi fi cation.Kernel fuzzy c-means(KFCM)with automatic variable weighting was investigated,which uses the adaptive distances to learn the weights of the variables during the clustering[10].Krinidis et al.,according to the window size information,presented a robust fuzzy local information c-means(FLICM)clustering algorithm[11].However,the noises were ampli fi ed due to the window size information.To extend FLICM to the higher dimensions,Krinidis et al.introduced a generalization clustering algorithm based on the fuzzy local information c-means (GFLIM)[12].On the basis of FLICM,Gong et al.developed a trade-off weighted fuzzy factor for controlling adaptively the local spatial relationship[13].To detect the moving objects, Chiranjeevi et al.used multi-channel kernel fuzzy correlogram based on background subtraction[14].Alipour et al.proposed a fast spatial kernel fuzzy c-means(FKFCM)to realize automatic medical image segmentation by connecting it with level set method[15].This FKFCM summarizes that kernel function attaches more weight to nearer pixels.Lu et al.reported amodi fi ed fuzzy c-means algorithm which involves a novel density-induced distance metric based on the relative density degree to improve classi fi cation[16].Qiu et al.introduced an enhanced interval type-2 fuzzy c-means(EIT2FCM)algorithm with improved initial center[17].In the aspect of robustness estimation[18-21],the theory and analysis processing were described.Nevertheless,these FCM algorithms based on kernel are dif fi cult to reduce the time consumption and optimize data center resources.

To deal with the above mentioned problems,a new robust dataset classi fi cation approach is presented based on neighbor searching and kernel fuzzy c-means(NSKFCM).The approach fi rst adopts the neighbor searching method with the dissimilarity matrix to normalize the dataset,and the number of clusters is determined by controlling clustering shape.To ensure the stability and consistency of classi fi cation,the maximum peak method is then used to initialize the membership and the cluster prototype.The adaptive distance kernel function is next employed to get the variable weights,followed by the convergence analysis of the objective function.Because dataset classi fi cation is an essential fundament of computational intelligence in CPS,numerical experiments are validated from practical MEMS accelerometer and the image segmentation to reduce the impact of parameters uncertainties with the complex datasets.The experimental results demonstrate the feasibility and robustness of NSKFCM.

The remainder of the paper is organized as follows.Section II brie fl y describes the fundamental kernel FCM algorithms. The NSKFCM approach and robustness estimation are described in Section III.Experimental results and comparative analysis are given in Section IV and the conclusions are summarized in Section V.

II.KERNEL FUZZY C-MEANS ALGORITHM

This section presents the notion of the fundamental kernel fuzzy c-means(KFCM)clustering algorithms[14].

A.Clustering Objective Function

LetR={x1,x2,...,xn}be a dataset,the objective function based on fuzzy clustering is[2]

where the arrayU={uik}represents a membership matrix satisfying

andV=denotes the vector of the cluster prototype. The parameterm∈(1,∞)is the weighting exponent,which determines the fuzziness number of classi fi cation.dikis the distance measure betweenxkandvi,de fi ned by

Here,[A]n×nis a symmetric positive de fi nite matrix.IfAis a unit matrix,the distance measure denotes the Euclidean distance.

FCM is non-robust because it ignores spatial contextual information and uses Euclidean distance.The feature space is then investigated,which uses a nonlinear mapping Φ from the input space datasetR={x1,x2,...,xn}to a higherdimensional space datasetF.So that the nonlinear mapping is simply represented by Φ:R→F.Since the key idea of kernel method is unnecessary to explicitly specify Φ,the objective function of KFCM in feature space(KFCM-F)is expressed by[22]

The kernel functionKis symmetric(i.e.,K(xk,xi)=K(xi,xk)),andK(xk,xi)=Φ(xk)TΦ(xi).Settingd(xk,vi)Δ=‖Φ(xk)-Φ(vi)‖,the objective function of KFCM-F is equal to

B.Membership and Cluster Prototype

For anyi∈{1,2,...,c},uikis the fuzzy membership degree and it satis fi esP=1.Based on the FCM membership[22]uik,which is given by

The KFCM-F membership degree is de fi ned as follow:

The cluster prototypeviis obtained as

Note that the KFCM algorithm based on Gaussian kernel function is sensitive to the noise.

III.THE ROBUST DATA CLASSIFICATION APPROACH

Several methods based on FCM need to determine the number of clusters,the iterations and the membership initialized randomly,in advance.Although it is dif fi cult to exactly determine these parameters,they have a great effect on the results. Zhang et.al.[23]adopt the weighted and hierarchical af fi nity propagation(WAP)to detect the changes of the data stream in real time,but the robustness does not be veri fi ed.Taking into account these reasons,a robust dataset classi fi cation approach is proposed based on neighbor searching and kernel FCM (NSKFCM).

A.Neighbor Searching

De fi nition 1.The dissimilarity matrix(also called distance matrix)[24]describes pairwise distinction betweennobjects.It is a square symmetricaln×nmatrix and can be represented by[d(i,j)]n×n,whered(i,j)≥0,d(i,i)=0 andd(i,j)=d(j,i).

If an asymmetrical relation exists between two objects(i.e.xiandxj),employing a simplicial scalar(such as distance) is insuf fi cient to further analyze the correlation between these two objects.The dissimilarity matrix is thus introduced to the initial data in NSKFCM approach.Given a datasetR={x1,x2,...,xn}consisting ofnobjects,max(x)and min(x)represent the maximum and minimum of the dataset, respectively.xi′represents the normalized object ofxi,which is de fi ned asIt represents the relative location ofxibetween the maximum and minimum. Hence the dissimilarity distanced(i,j)is given asd(i,j)=whereαis the positive weighting coef fi cient. The dissimilarity matrixDis accordingly structured as

Equation(10)establishes the relative distance of the distinct objects,but it is dif fi cult to make the subsequent clustering analysis.In order to facilitate the subsequent analysis,the dissimilarity matrix needs to be normalized.Based on the dissimilarity distance,the Jaccard measure[25-26]is used for interpreting the similarity of the distinct objects.The normalization matrix[G]n×nis then speci fi ed as

here the mean distance of the normalized objects is involved, which can better demonstrate the object’s detailed information.The normalization matrix is a symmetric matrix,which takes values from 0 to 1,and it contains the relationship ofGi,j=Gj,i.With the similarity matrix,the original datasetRis normalized by[G]n×n.

De fi nition 2.For the datasetR={x1,x2,...,xn}and any objectxi,2≤i≤n-1,objectsxi-1andxi+1are called the neighbors ofxi.Ifi=1,the neighbor ofx1isx2,and ifi=n,the neighbor ofxnisxn-1.

De fi nition 3.Referring to[27-28],for a datasetR={x1,x2,...,xn},setting the objectyand the distancer,if any objectxisatis fi esd(xi,y)≤r,thenxiis the direct neighbor ofy.The entire neighbors set of objectyare represented byDy,and 0≤r≤1 adopts the Jaccard coef fi cient.It is the maximum distance if two objects are neighbors.

As shown in Fig.1,the given dataset is divided into two clusters,A={a,b,c,...}andB={f,...}.

Fig.1.Clustering example.

The neighbor searching method is able to traverse the objects.Ifd(x,y)≤r,the objectxandyare neighbor in the same neighbor set.Supposingr=0.65,d(a,b)=0.50,d(b,c)=0.60,d(c,d)=0.63,d(d,e)=0.50 andd(e,f)= 0.62,the objectsb,c,d,eandfwill be sequentially merged intoA={a,b,c,d,e,f,...}.Considering this,the neighbor searching depending only on the distance cannot be properly achieved.The parameter of controlling cluster shape is then presented in De fi nition 4.

De fi nition 4.Given a datasetA={x1,x2,...,xm}includesmobjects,andyis another object,ifd(xi,y)≤r, thenXi=1,elseXi=0.The other objectyis merged intoAsatisfying/m≥ξ[28].ξis named the parameter of controlling clustering shape and 0≤ξ≤1.

Considering the above de fi nitions and Fig.1,the neighbor sets ofa,bandcare expressed asDa,DbandDc,respectively. The given three neighbors havem=3.The analysis forecan be merged intoAare shown as follows.

1)Ifξm=1,then=1,i.e.,d(a,e)≤r, ord(b,e)≤r,ord(c,e)≤r.The condition ise∈(Da∪Db∪Dc).

2)Ifξm=2,then=2,i.e.,d(a,e)≤r∩d(b,e)≤r,ord(b,e)≤r∩d(c,e)≤r,ord(c,e)≤r∩d(a,e)≤r.The condition satis fi ese∈((Da∩Db)∪(Db∩Dc)∪(Da∩Dc)).

3)Ifξm=3,thenP=3,i.e.,d(a,e)≤r,d(b,e)≤randd(c,e)≤r,satisfyinge∈(Da∩Db∩Dc).

The analysis indicates that ifξis larger,the clustering region is smaller,and the number of clusters is more.The neighbor searching method is used to ascertain the number of clusters.

B.Initialization of Membership and Cluster Prototype

The majority of FCM clustering algorithms employ the membership initialized randomly,the clustering result is then varied each time.NSKFCM involves the maximum peak method to search the cluster prototype.Given a datasetR={x1,x2,...,xn},the maximum peak method,whose dataset is de fi ned asP={p1,p2,...,pk},will be executed in the following steps.

1)Searchthemaximumpeakbypk= argmaxx{xi-1,xi,xi+1}⊆P,2≤i≤n-1,herekexpresses the number of maximum peak.

2)Calculate the sum of each neighbor set.

3)Remove the minimum peak.cis the number of clusters withc∈[1,n].Ifk＞c,the minimum peak is removed fromP.Set ask=k-1 and return to 2).

4)Con fi rm the initialized cluster prototype.Ifk=c,it is de fi ned as

wheretis the interval of every cluster prototype.

5)Calculate the initialized membership given in(6), whereinrepresents the distance. The cluster prototype vector and membership matrix have been initialized,consequently,they are the fi xed values to ensure the stability of classi fi cation.

C.Optimization of Membership and Cluster Prototype

The traditional kernel clustering methods do not take into account the relevance weights of the variables[14].NSKFCM adapts the Gaussian kernel function to apply each variable. The kernel function is written as(14).

The approach investigates an optimized adequacy criterion of objective function,which can be de fi ned as

In accordance with the dissimilarity matrix,φ2(xk,vi)is equal to

Proposition 1.For the distance function(16),and ifK(·,·) is the Gaussian kernel,then with fi xedVandλ,the fuzzy membershipdegreeuik(k=1,2,...,n,i=1,2,...,c), which minimizes the objective functionO(U,V,λ)given in (17),underuik∈[0,1],∀i,kandP=1,∀k,satis fi es the local optimum expressed by

The proof is given in Appendix A.

Proposition 2.For the distance function(16),andK(·,·) as the Gaussian kernel,and with fi xedUandλ,then the cluster prototypevij(i=1,2,...,c,j=1,2,...,t),which minimizes the objective functionO(U,V,λ)given in(17), is optimized by the following expression:

The proof is given in Appendix B.

NSKFCM based on adaptive distances is used for determining the weights of the variables.Having fi xed the fuzzy membership matrixUand cluster prototype vectorV,minimizing the objective functionO(U,V,λ)is constrained by the weights of the variables.

Proposition 3.If the adaptive distance function is given by(16),the vector of weightλ=(λ1,λ2,...,λt),which minimizes the objective function(17)underλj＞0,∀jand=1,λj(j=1,2,...,t)is updated according to the following expression:

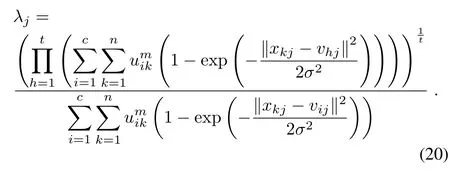
The proof is achieved in Appendix C.

Remark 1.It is important to note that NSKFCM converges to a local minimum or a saddle point.

Considering the convergence theory for fuzzy c-means[29], the relationship of the objective function(17)between neighboring objects,under Propositions 1,2,and 3 given in(18), (19),and(20),is presented as the following form:

This conclusion holds that the bounded objective functionO(U,V,λ)is a decreasing function during iteration.NSKFCM will eventually converge to a local minimum or a saddle point.

D.Robustness Estimation

An excellent clustering algorithm should be robust to reject the ubiquitous exogenous noises with the uncertain outliers[18-19].Since the objective functions of NSKFCM probably have several local optimums,it is necessary to establish robust estimator for evaluating the impacts of the critical parameters.The considered fundamental robust estimator is M-estimator,which can facilitate an optimizer for the objective function[30].

Given a random dataset asR={xi,i=1,2,...,n},with the aid of M-estimator,the estimation parameterθis designed as

whereFX(x)represents the distribution function ofX.The in fl uence function is the important measure of robustness,and if the estimator is bounded,the parameters uncertainties are robust.

Based on(18)-(20),it is concluded that the uni fi ed form (i.e.,(xkj-vij))can be involved in the Gaussian kernel. Therefore,according to the NSKFCM approach,an arbitrary uncertain functionF(θ)is considered as

The functionφ(x-θ)with(26)is bounded and continuous.It is proved that the involved M-estimator designs a bounded and continuous in fl uence function,and the impacts of parameters uncertainties are robust.

To qualitatively evaluate the robustness against the parameters uncertainties,the impact ofρ(x-θ)is analyzed by the following numerical examples.

The calculated results of prototype function and M-estimator are illustrated in Figs.2(a)and 2(b),respectively. Fig.2(a)shows that the maximum ofρ(x-θ)is existed and bounded.Fig.2(b)demonstrates that the parameterθfl uctuates smoothly due to limx→∞φ(x-θ)=0 and the evolution curve converges to the equivalent point 0.From (18)-(20),it indicates that the proposed method re fl ects the good robustness against the parameters uncertainties ofuij,vijandλj.

Fig.2.Convergence effect analysis.

E.NSKFCM Approach Steps

The proposed NSKFCM approach is executed as the following steps.

Algorithm 1.NSKFCM algorithm.

Input.The distancerand the factor for controlling cluster shapeξ;

The kernel method parameterσ;

The stop thresholdεand fuzzy weighting exponentm;

Output.

The fuzzy membership matrixU,the cluster prototype vectorVand the objective valueO(U,V,λ);

1)Determine the number of clusters by settingrandξadopting to the neighbor searching method.

2)InitializeUandVin thei-th cluster dataset,under(6),(13) and the number of clusters.

3)Set the bandwidth parameterσand the fuzzy weighting exponentm,with 0＜ε≪1.

4)UpdateUin accordance with(18).

5)UpdateVaccording to(19).

6)Updateλdepending on(20).

7)If the stopping criterion satis fi esthen stop the iteration,and output the fuzzy membership matrixUand cluster prototype vectorV.Otherwise,set asiter=iter+1 and return to 4).

8)returnU,VandO(U,V,λ).

IV.EXPERIMENT VERIFICATION

The experiment section will describe the dataset classi fi cation approach which is achieved to the dynamic behavior of MEMS accelerometer and the landscape images segmentation.

A.Experiment 1:MEMS Accelerometer Dataset

MEMS accelerometer is a kind of sensor.The top view of the accelerometer is shown as Fig.3 The accelerometer is an ARM Cortex-M3 microcontroller.

Fig.3.The detectable direction.

The datasets achieved from the MEMS accelerometer are three matrices on theX/Y/Zaxes directions.The dynamics in the horizontal and vertical orientations are shown in Fig.4, which represents the movement time and acceleration,respectively.From a large number of experiments,the movement directions including horizontal,vertical,up and down,are obtained,whereas the runtime of the accelerometer is 5 minutes.

NSKFCM is able to solve how to classify the dataset from noises and error values.A group of experiments are performed to compare NSKFCM with other methods,including AFCM[3], EnFCM[6],KFCM[14],FKFCM[15],FLICM[11].

The parameters are set in accordance with a large number of veri fi cations,in general,given the weighting exponentm=2, the stop thresholdε=1×10-5,the bandwidth parameterσ=15,the maximum of iterationiter=200,and the number of clusters=4.In addition,for the NSKFCM, when the critical parameterrandξare set as different values, the number of clusters is different.The numerical experiments are shown as Figs.5(a)-(h).

Comparing the experimental results of the six methods,the classi fi cation effects are re fl ected by the following aspects.

1)AFCM employs a new metric distance whose value is less than 1 during iteration.The dataset is classi fi ed to one class, consequently,the algorithm cannot accomplish the dataset classi fi cation for the accelerometer dynamic behavior.

Fig.4.The dynamic behavior onYaxis.

2)EnFCM is ef fi cient,which involves the biased solution toward piecewise homogeneous labeling.Since the result is piecewise partition according to the label interval,the algorithm does not distinguish the dynamic behavior of acceleration dataset.

3)The distance metric of KFCM adopts the space data kernel function.This factor depends on the spatial symmetry data,so that the classi fi cation is in fl uenced by more noises and outliers.

4)The major characteristic of the FKFCM is the kernel function which has given greater weight value to the neighbor data.However,the number of clusters needs to be judged based on experience.

5)More local context information are used to reduce the iterations for FLICM algorithm.However,the local coef fi cient of variation is unreasonable to ignore the in fl uence of spatial constraints.

6)NSKFCM sets three groups of parameters.Given differentrandξ,the dataset are divided into different classes.The clustering results are accurate.MEMS accelerometer dataset is able to be automatically judged by the number of clusters and accurately classi fi ed the dynamic behavior of acceleration dataset on different times.

The optimal effectiveness indicators(OEI)are proposed to analyze the robustness.It expresses the average of the correctly classi fi ed data,OEI is greater as well as the classi fi cation is more accurate.

Table I shows the quantitative comparison indicators of the experiments on the MEMS accelerometer dataset for the accuracy of the dataset classi fi cation.

From the measures of Table I,it indicates that NSKFCM is superior to the other compared algorithms on the aspects of OEI,the time consumption and the number of iterations. The results illustrate that the proposed NSKFCM approach possesses the optimal performance index for dataset classi fication.

Fig.5.The dataset classi fi cation of each algorithm.

TABLE I NUMERICAL RESULTS ON THE PRACTICAL MEMS DATASET

B.Experiment 2:Landscape Images Segmentation

The dataset classi fi cation is applied to CPS.In the computer vision,the 2D dataset fromX/Yaxis of accelerometer is similar to the 2D image.Therefore,these data are treated as classi fi cation for image segmentation.

In the coming experiments,four methods are applied to three landscape images.The fi rst natural image contains mountain and cloud,with 304×208 pixels.

The number of clusters is 4 as shown as Figs.6(b)-(d), which are the segmentation results obtained by EnFCM, KFCM and FLICM,respectively.Figs.6(e)-(f)display the NSKFCM segmentation results.The numbers of clustering are 2 and 4,whenr=0.5,ξ=0.4 andr=0.5,ξ=0.7. The image segmentation results illustrate that the proposed approach is robust and maintains the clear image edges and the more details.

Fig.6.The segmentation result of original landscape contains mountain and cloud.

Fig.7(a)shows the original landscape image containing cloud,plain and forest,with 308×200 pixels.Figs.7(b)-(d) demonstrate the segmentation results,the number of clusters is 4.For NSKFCM,whenr=0.6,ξ=0.3 andr=0.6,ξ=0.7, the numbers of clustering are 3 and 7.From Figs.7(e)-(f),the experiment results show that NSKFCM is able to reject noises while preserving signi fi cant image details and obtain superior performance.In particular,it is relatively independent of the type of textures.

Fig.7.The segmentation result of original landscape contains cloud, plain and forest.

Finally,Figs.8(a)-(f)validate the segmentation results of original landscape image including cloud,mountain,plain and tree,with 308×207 pixels.Figs.8(b)-(d)are the segmentation results obtained by EnFCM,KFCM and FLICM.Shown in Figs.8(e)-(f),the factors are modi fi ed asr=0.6,ξ=0.5 andr=0.6,ξ=0.9,the segmentation results are 4 classes and 7 classes,respectively.The clear image edges are obtained and the landscape types are segmented.

In order to evaluate the performance of these four methods and analyze the robustness,some optimal indicators are introduced.The reconstruction rate(RR)de fi nes the image reconstructed indicator as

Average max membership(AMM)is expressed as

Fig.8.The segmentation result of original landscape contains cloud, mountain,plain,and tree.

The quality(Q)of the image segmentation is described as

The average of membership variance(AMV)is represented as

The average of the membership difference between maximum value and current value(AMD)is shown

Table II compares the quantitative comparison indicators of the experiments on three natural images for the accuracy of image segmentation.From the performance parameters shown in Table II,NSKFCM adopts the neighbor searching method with the dissimilarity matrix,and the adaptive distance kernel function is employed to evolve the variable weights.It does not require a preset the number of clusters,which is determined byrandξ.Furthermore,kernel function performs a nonlinear data transformation into high dimensional feature space,it increases the probability of the linear segmentation within the transformed space.To ensure the stability and consistency of the classi fi cation,the maximum peak method is used for initializing the membership degree and cluster prototype.The segmentation results of NSKFCM possesses more excellent performance,less iterations number,lower time consumption and higher ef fi ciency than the other methods.

V.CONCLUSION

With the aid of neighbor searching and kernel fuzzy c-means methods,the corresponding dataset classi fi cation application for CPS is discussed in this work.A novel robust dataset classi fi cation approach is investigated for accurately classifying the complex dataset of CPS.Compared with the existing literatures,the proposed method shows better adaptiveness and robustness in complex dataset classi fi cation.As a theoreticalresult,the dynamic behavior of acceleration dataset is improved and the impact of parameters uncertainties is reduced. In numerical validations,several images-induced datasets are employed,and the results show that the desired image edges are clari fi ed and texture details are effectively obtained.Based on this paper,our future work will concentrate on further improving the accuracy of the accelerometer,the high-dimension dataset classi fi cation,and the 3D segmentation for spatial points and images.

TABLE II NUMERICAL RESULTS OF THE FOUR METHODS ON THREE LANDSCAPE IMAGES

APPENDIX A PROOF OFPROPOSITION1

Similarly,usinguhk,h=1,2,...,creplacesuik,and the restricted condition is satis fi ed by

Based on the matrix theory,the Hessian matrixH(φ(U))is a diagonal matrix.Due tom＞1 and 0≤uik≤1,H(φ(U)) is a symmetric positive de fi nite matrix.□

APPENDIX B PROOF OFPROPOSITION2

For the distance function(16),andK(·,·)as the Gaussian kernel,and with fi xedUandλ,then the cluster prototypevij(i=1,2,...,c,j=1,2...,t),which minimizes the objective functionO(U,V,λ)given in(17),is optimized by the following expression:

Proof.The Lagrange equation is constructed depending on the objective function

In order to prove the suf fi cient condition,the Hessian matrix is involved.Settingφ(V)=O(U,V,λ),the Hessian matrixH(φ(V))corresponding toφ(V)is shown referring to(B.1), (B.2)and(B.3)

It is obtained thatH(φ(V))is a diagonal matrix,from(B.4), and also a symmetric positive de fi nite matrix.□

APPENDIX C PROOF OFPROPOSITION3.

If the adaptive distance function is given by(16),the vector of weightλ=(λ1,λ2,...,λt),which minimizes the objective function(17)underλj＞0,∀jand=1,λj(j=1,2,...,t)is updated according to the following expression:

if max(λi1,λi2,...,λit)=(1,1,...,1),(C.6)is replaced by (C.7)

Therefore,the extremum is the minimizing objective function.The vector of weightλjis updated by the following expression

ACKNOWLEDGEMENT

The authors would like to thank SENODIA Technologies Incorporation for providing the MEMS accelerometer sensor.

REFERENCES

[1]Dunn J.A graph theoretic analysis of pattern classi fi cation via Tamura’s fuzzy relation.IEEE Transactions on Systems,Man,and Cybernetics, 1974,SMC-4(3):310-313

[2]Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms.New York:Springer,1981.

[3]Wu K L,Yang M S.Alternative c-means clustering algorithms.Pattern Recognition,2002,35(10):2267-2278

[4]Ahmed M N,Yamany S M,Mohamed N,Farag A A,Moriarty T. A modi fi ed fuzzy c-means algorithm for bias fi eld estimation and segmentation of MRI data.IEEE Transactions on Medical Imaging, 2002,21(3):193-199

[5]Chen S C,Zhang D Q.Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics, 2004,34(4):1907-1916

[6]Szilagyi L,Benyo Z,Szilagyi S M,Adam H S.MR brain image segmentation using an enhanced fuzzy c-means algorithm.In:Proceedings of the 25th Annual International Conference on Engineering in Medicine and Biology Society.Cancun,Mexico:IEEE,2003.724-726

[7]Li C F,Liu L Z,Jiang W L.Objective function of semi-supervised fuzzy c-means clustering algorithm.In:Proceedings of the 6th IEEE International Conference on Industrial Informatics.Daejeon,Korea: IEEE,2008.737-742

[8]Huang S B,Cheng Y,Wan Q S,Liu G F,Shen L S.A hierarchical multi-relational clustering algorithm based on IDEF1x.Acta Automatica Sinica,2014,40(8):1740-1753(in Chinese)

[9]Wang L,Gao X W,Wang W,Wang Q.Order production scheduling method based on subspace clustering mixed model and time-section ant colony algorithm.Acta Automatica Sinica,2014,40(9):1991-1997(in Chinese)

[10]Ferreira M R,De Carvalho F D A T.Kernel fuzzy c-means with automatic variable weighting.Fuzzy Sets and Systems,2014,237:1-46

[11]Krinidis S,Chatzis V.A robust fuzzy local information c-means clustering algorithm.IEEE Transactions on Image Processing,2010,19(5): 1328-1337

[12]Krinidis S,Krinidis M.Generalised fuzzy local information c-means clustering algorithm.Electronics Letters,2012,48(23):1468-1470

[13]Gong M G,Liang Y,Shi J,Ma W P,Ma J J.Fuzzy c-means clustering with local information and kernel metric for image segmentation.IEEE Transactions on Image Processing,2013,22(2):573-584

[14]Chiranjeevi P,Sengupta S.Detection of moving objects using multichannel kernel fuzzy correlogram based background subtraction.IEEE Transactions on Cybernetics,2014,44(6):870-881

[15]Alipour S,Shanbehzadeh J.Fast automatic medical image segmentation based on spatial kernel fuzzy c-means on level set method.Machine Vision and Applications,2014,25(6):1469-1488

[16]Lu C H,Xiao S Q,Gu X F.Improving fuzzy c-means clustering algorithm based on a density-induced distance measure.The Journal of Engineering,2014,1(1):1-3

[17]Qiu C Y,Xiao J,Han L,Naveed Iqbal M.Enhanced interval type-2 fuzzy c-means algorithm with improved initial center.Pattern Recognition Letters,2014,38:86-92

[18]Cand´es E J,Li X D,Ma Y,Wright J.Robust principal component analysis.Journal of the ACM(JACM),2011,58(3):Article No.11

[19]Yang M S,Lai C Y,Lin C Y.A robust EM clustering algorithm for Gaussian mixture models.Pattern Recognition,2012,45(11):3950-3961

[20]Elhamifar E,Vidal R.Robust classi fi cation using structured sparse representation.In:Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition(CVPR).Providence,RI,USA:IEEE, 2011.1873-1879

[21]Xie X M,Wang C M,Zhang A J,Meng X F.A robust level set method based on local statistical information for noisy image segmentation.Optik-International Journal for Light and Electron Optics,2014,125(9): 2199-2204

[22]Filippone M,Camastra F,Masulli F,Rovetta S.A survey of kernel and spectral methods for clustering.Pattern Recognition,2008,41(1): 176-190

[23]Zhang J P,Chen F C,Li S M,Liu L X.Data stream clustering algorithm based on density and af fi nity propagation techniques.Acta Automatica Sinica,2014,40(2):277-288(in Chinese)

[24]Kantardzic M.Data Mining:Concepts,Models,Methods,and Algorithms.Second Edition.New York:John Wiley&Sons,2011.249-259

[25]Anderson M J,Ellingsen K E,McArdle B H.Multivariate dispersion as a measure of beta diversity.Ecology Letters,2006,9(6):683-693

[26]AndersonMJ,Santana-GarconJ.Measuresofprecisionfor dissimilarity-based multivariate analysis of ecological communities.Ecology Letters,2015,18(1):66-73

[27]Cormen T H,Leiserson C E,Rivest R L,Stein C.Introduction to Algorithms.Cambridge:MIT Press,2001.1-7

[28]Qian J B,Dong Y S.A clustering algorithm based on broad fi rst searching neighbors.Journal of Southeast University(Natural Science Edition),2004,34(1):109-112(in Chinese)

[29]Bezdek J C,Hathaway R J,Sabin M J,Tucker W T.Convergence theory for fuzzy c-means:counterexamples and repairs.IEEE Transactions on Systems,Man,and Cybernetics,1987,17(5):873-877

[30]Shahriari H,Ahmadi O.Robust estimation of the mean vector for high-dimensional data set using robust clustering.Journal of Applied Statistics,2015,42(6):1183-1205

[31]Kinoshita N,Endo Y.EM-based clustering algorithm for uncertain data.Knowledge and Systems Engineering,2014,245:69-81

[32]Gao J,Wang S T.Fuzzy clustering algorithm with ranking features and identifying noise simultaneously.Acta Automatica Sinica,2009,35(2): 145-153(in Chinese)

Li Liu Ph.D.candidate at the School of Mechatronic Engineering and Automation,Shanghai University, China.She received the B.Sc.degree from Qufu Normal University,China in 2004.She received the M.Sc.degree from Dalian Maritime University, China in 2007.She is also a lecturer at the School of Information Science and Electrical Engineering, Ludong University,China.

Her research interests include machine vision and image processing.

His research interests include cooperative control of multiagents,formation fl ight control of unmanned aerial vehicles,image processing and machine vision,and wireless networked control systems.Corresponding author of this paper.

Wenju Zhou received the Ph.D.degree from Shanghai University,China,in 2014.He received the B.Sc. degree and M.Sc.degree from Shandong Normal University,China,in 1990 and 2005,respectively. He is currently a robotic engineer at the School of Computer Science and Electronic Engineering, University of Essex UK,and the associate professor at the School of Information and Electronic Engineering,Ludong University,China.

His research interests include intelligent control, machine vision,and the industry applications of the automation equipment.

Xiaofeng Zhang received the Ph.D.degree from the School of Computer Science and Technology, Shandong University,China,in 2014.He received the M.Sc.degree from the School of Computer and Communication,Lanzhou University of Technology, China in 2005.Now he is a lecturer at the School of Information and Electrical Engineering,Ludong University,China.

His research interests include medical image segmentation,pattern recognition,etc.

Minrui Fei Professor at Shanghai University,vicechairman of Chinese Association for System Simulation,and standing director of China Instrument& Control Society.He received the B.Sc.,M.Sc.and Ph.D.degrees all from Shanghai University,China, in 1984,1992,and 1997,respectively.

His research interests include networked advanced control and system implementation,distributed and fi eldbus control systems,key technology and applications in multi- fi eldbus conversion and performance evaluation,as well as the application of virtual reality and digital simulation in industry.

Xiaowei Tu received the Ph.D.degree from University of Technology of Compiegne(UTC),France in 1987.He worked as professor in UTC,and later he became a researcher in French National Research Center(CNRS)in early 1990s.Since 1997,he has been working also as a researcher and R&D project manager in different Canadian research institutes.He is currently a professor at the School of Mechatronic Engineering and Automation,Shanghai University, China.

His research interests include robotic vision,industrial inspection,and industrial automation.

g

the Ph.D.degree in intelligent system and control from Queen’s University Belfast, UK in 2012,the M.Sc.degree in control theory and control engineering from Shanghai University, China in 2009,and the B.Sc.degree in electronic engineering from Hubei University of Technology, China,in 2004.He is currently a lecturer at the School of Mechatronic Engineering and Automation, Shanghai University,China.

Manuscript received October 10,2014;accepted April 28,2015.This work was supported by National Natural Science Foundation of China (61403244,61304031),Key Project of Science and Technology Commission of Shanghai Municipality(14JC1402200),the Shanghai Municipal Commission of Economy and Informatization under Shanghai Industry-University-Research Collaboration(CXY-2013-71),the Science and Technology Commission of Shanghai Municipality under‘Yangfan Program’(14YF1408600), National Key Scienti fi c Instrument and Equipment Development Project (2012YQ15008703),and Innovation Program of Shanghai Municipal Education Commission(14YZ007).Recommended by Associate Editor Jiming Chen.

:Li Liu,Aolei Yang,Wenju Zhou,Xiaofeng Zhang,Minrui Fei,Xiaowei Tu.Robust dataset classi fi cation approach based on neighbor searching and kernel fuzzy C-means.IEEE/CAAJournalofAutomaticaSinica, 2015,2(3):235-247

Li Liu,Aolei Yang,Minrui Fei,and Xiaowei Tu are with Shanghai Key Laboratory of Power Station Automation Technology,School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China (e-mail:liulildu@163.com;aolei.yang@gmail.com;mrfei888@x263.net;xiaoweitu@hotmail.com).

Wenju Zhou is with the School of Computer Science and Electronic Engineering,University of Essex,Colchester CO4 3SQ,UK(e-mail: wzhoua@essex.ac.uk).

Xiaofeng Zhang is with the School of Information Science and Electrical Engineering,Ludong University,Yantai 264025,China(e-mail: iamzxf@126.com).