一种基于SIFT的三角网格图像匹配方法

郭全民，胡晓星

（西安工业大学电子信息工程学院，西安710021）

一种基于SIFT的三角网格图像匹配方法

郭全民，胡晓星

（西安工业大学电子信息工程学院，西安710021）

针对影像对匹配过程中，由于场景复杂，干扰严重，导致错误匹配率较高的问题，提出一种在三角形约束下，基于SIFT（Scale Invariant Feature Transform）算法的图像匹配策略。该方法大致分两步进行，首先是粗匹配，使用SIFT算法和Harris选择区别度较高的特征点，得到良好特征点集。第二步为细匹配，根据良好点集建立Delaunay同名三角网格，对同名三角形再次使用SIFT算法提取特征点进行匹配。实验表明，提出的算法一定程度上提高了特征点复现率和匹配准确率。

SIFT特征；Harris特征；自适应非最大抑制；Delaunay三角形；特征提取；特征匹配

1 引 言

长期以来制约数字摄影测量与计算机视觉自动化及可靠性的一个关键问题就是立体影像对的匹配，即在立体影像对的重叠区域内以影像匹配代替（或模拟）人眼立体观察自动寻找同名像点的过程。然而，面对千变万化的影像，现有的影像匹配方法仍然存在许多问题，尤其是在植被茂密、建筑物密集和水域等区域影像匹配的可靠性还不高，建筑物角点和一些地物的主要边界点还不能被自动地匹配出来，自动产生的数字表面模型存在着许多异常值，需要进行大量的人工编辑处理。

匹配难度大的部分原因是图像缺失或者噪声使匹配成为一个病态问题。通常，利用先验知识也就是运用附加的假设或约束将影像匹配从一个“病态”问题转化为“良性”问题。如对极几何约束等，通过构建优化函数，优化匹配质量。近几年针对SIFT的特征匹配策略改进涌现出很多创新。其中，文献［1］结合SURF算法和Delaunay三角网来提高匹配正确率。文献［2］提出了一种基于圆形区域和Harris角点检测的图像配准算法，充分利用圆形区域的旋转不变性和互信息量最大原则进行特征点匹配。文献［3］提出一种基于良好匹配点三角形局部连续性约束下的影像匹配方法，该方法使用改进的Harris算法提取特征点，并且使用核线约束和灰度相关约束得到可靠性高的同名点。文献［4］提出了结合区域分割的SIFT方法，将图像分成边缘集中区域和非集中区域，设置一块或者几块ROI区域作为SIFT特征提取的对象。

David Lowe于2009年提出SIFT算法［5］（Scale Invariant Feature Transformation），提取出的特征点具有尺度，旋转，平移和缩放不变性，并对仿射和广光照变化具有一定的不变性。是一种鲁棒性较强的特征提取算法。文中提出了一种基于SIFT算法的匹配策略，利用良好匹配点三角形局部连续性约束进行匹配来提高匹配正确率。

2 基于三角形约束的影像匹配原理

算法流程如图1所示，详细介绍如下：

（1）利用SIFT算法提取特征点。先使用SIFT算法提取特征点，在较高的匹配阈值下（实验中一般为0.4）选取差异性大正确率高的特征点。

（2）利用Harris算法筛选稳定的特征点。文献［6］提出，由于与基于自相关性的检测器不同，虽然SIFT算法在实际应用中效果较好，但是其特征点提取理论并不是基于最大化空间稳定性。所以，文中使用Harris算法［7］过滤出角点响应强度较高的稳定点集。

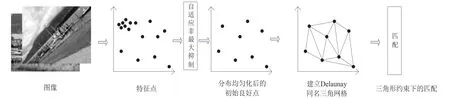
图1 基于SIFT的Delaunay三角网格匹配方法

（3）应用自适应非最大抑制（ANMS）使特征点分布平均化。

由于特征点检测器仅寻找兴趣函数的局部最大值，得到的匹配点通常分布不均匀，在纹理丰富的区域密集，而缺少纹理的区域以及视差不连续的区域密度较小，甚至没有，导致不能构建面积大小合适的三角形区域。文中使用自适应非最大抑制（ANMS）［8］算法去除部分密集处的特征点，得到分布较均匀的良好点集合。

这时得到的匹配点对仍存在少许错匹配，实验中为图像对匹配连线的长度和倾斜角度分别设置一个阈值，去除部分明显的错误匹配。

在每幅影像上自动提取出数以百计的备选匹配特征点，经过严格的粗检测和剔除，那些剩下的特征点被认为是最初始的良好点（纹理特征明显、匹配正确、分布均匀），因此可以作为后续密集匹配的可靠先验知识。

（4）生成Delaunay同名三角形对

假设经过筛选后剩余的点均是初始良好点，也就是种子点中不存在错误匹配。提出的算法采用Delaunay三角形法则在立体像对上构建同名三角网。将第一幅建立Delaunay三角形网格的影像称为主图，待匹配的图称为辅图，也就是根据主图中Delaunay三角网格中特征点的顺序，建立三角网格，并以辅图中同名点的顺序在辅图中插入三角网格，最后得到同名三角形对。

（5）再次使用SIFT算法进行细致匹配

在三角网格的约束下，对同名三角形对区域内的图像进行特征提取并匹配。需要注意的是，文中选择NNDR（最近邻距离比率）作为匹配策略，即通过比较最近邻和次近邻距离，确定匹配点对。经过多次实验，初始匹配的阈值为0.4，细致匹配的阈值为0.6，当图像失真严重程度增加时，如仿射变化较大，通过增加初始匹配和细匹配的阈值，会降低特征点质量，提高匹配对数量，反之，则提高特征点质量，降低匹配点对数量。

（6）匹配效果评价标准

特征匹配时，使用次近邻准则进行匹配。匹配的阈值即NNDR（最近距离比值）的高低直接影响匹配的数量和质量。提出的算法使用下面的定义来计算正确和错误匹配以及匹配失败的数目。提出的算法使用PPV（肯定预测值），将得到的实验结果转化为单位比率。

其中，TP（正确肯定）为正确匹配的数目，FP（误报）为给出的匹配中不正确的数量。TP与FP的和等于实际肯定的数目，理想情况下，准确率PPV应该接近于1。

同时提出的算法使用复现率来衡量匹配结果的好坏。若在两幅图像中检测到的特征点个数分别为n1和n2，而在两幅图中均检测到的特征点个数也就是匹配对为n3，那么复现率定义为：

检测到的特征点复现率越高，则说明检测的性能越稳定，对匹配也就越有利。

3 实验结果与分析

为验证提出的算法可靠性、效率与精确度，采用CPU主频2.5GHz，RAM 2G，Windows 7系统，MATLAB 2009a开发平台实现上述讨论的影像匹配算法，使用牛津大学仿射协变标准图像集进行实验。这个数据集共有8个子集，包含5种图像变换：视点变化，尺度变化，图像模糊，JPEG压缩，光照变化。每个子集有6张图片，拍摄的是同一场景的不同情况，文中选取其中六个子集进行验证。

图2显示了对Wall图片集进行三角网格化，Wall子集含有透视失真和许多重复结构，属于图像集中最难匹配的例子。由图可知，一定的视角变换下，噪声点或特征点有丢失会使Delaunay三角网局部发生改变，但总体结构变化不大，而超过一定的仿射变换程度，得到的网格难以代表图像纹理和结构信息。

图2 对wall图片集进行Delaunay三角网格化

图3中下方两条线为SIFT（NNDR）方法的匹配效果和基于SIFT（NNDR）的改进匹配算法的复现率对比。中、下曲线分别对应其改进的算法和基于SIFT（NNDR）的复线率，反映了使用NNDR作为匹配准则的SIFT匹配结果和使用提出的匹配策略且NNDR作为匹配准则时的SIFT匹配效果对比，最上面的曲线为其改进算法的匹配准确度。每组图包含了对应子集的实验结果。下图中横坐标表示每一个测试子集中参考图像（失真度最轻）与其他5幅图像的效果对比，随着横坐标的增大，比对图像的失真程度越大。纵坐标包含SIFT使用NNDR算法匹配和提出的基于三角形网格的SIFT匹配算法的复现率对比，以及匹配算法改进后的匹配准确率。

图3（a）是视角变换和透视失真时的复现率和提出的改进算法准确率，图3（b）是重复纹理加透视失真下的复现率和改进算法准确率，图3（c）是亮度变化时复现率对比和改进算法准确率。可以看出wall和（a）图像集中，随着视角变化程度加大，改进算法的匹配准确率出现急剧恶化。然而，通过改变参数，提高初始特征点的数量，可以间接地提高匹配准确度。图3（d）是JPEG人工压缩变换下的复现率对比和改进算法准确率，图3（e）是旋转、尺度变化时的复现率对比和改进算法准确率，图3（f）是图像模糊和平移时的复现率对比和改进算法准确率。可以看出，在图3（d）、（e）、（f）中，均保持较高的匹配准确率。在每个子集中，用第一张图片与其余图像进行匹配，随着图像失真程度的加大，匹配任务难度增加，复现率和准确率都呈下降趋势。除了wall和（a）图像集，提出的方法均保持了较高的正确匹配率，且对于平移变换、尺度变化、旋转、亮度变化、模糊度变化等失真表现良好。

根据实验结果可以得到以下结论：

（1）由于采用了局部连续性约束方法，同名点的搜索区域显著缩小，基于三角网约束的匹配方法有效改善了特征的误匹配问题；

（2）大部分建筑物角点能够直接被匹配出来，从而提高了数字表面模型的可靠性和信息完整性；

（3）匹配点的生成遵循了纹理特征由显著到不显著的顺序，实现了与纹理自适应的、由粗略到细致的多级匹配，有利于提高重复纹理的匹配率；

（4）由于SIFT算法对仿射只具有一定程度的不变性，且初始良好点对匹配效果起主导作用，所以当视角变化较大时，无法得到足够的高初始良好点，导致后续的三角网格化效果急剧恶化。

图3 SIFT（NNDR）和其改进算法的复现率对比以及其改进算法的匹配准确度

4 结束语

针对大场景图像对特征匹配错误率较高的问题，文中提出了一种基于SIFT算法的匹配方法。该方法限制了点对的位置，舍弃了对图像变换敏感的点对间几何相关性实现降低匹配搜索空间的缩小。实验结果表明，该方法不仅对平移、缩放、旋转和一定程度的仿射等图像变换具有鲁棒性，还提高了匹配的正确率和特征点的复现率。

［1］ Yan ZiGeng，JIANG JianGuo，GUO Dan.Image matching based on SURF feature and delaunay triangular meshes［J］.Acta Automatica Sinica，2014，40（6）：1216－1222.

［2］ 刘贵喜，王蕾.基于区域选择和特征点匹配的图像配准算法［J］.光电子激光，2007，18（8）：999－1002.

LIU GuiXi，WANG Lei.An image registration method based on region selecting and feature points matching［J］.Journal of Optoelectronics Laser，2007，18（8）：999－1002.

［3］ 张云生.自适应三角形约束的多基元多视影像匹配方法［D］.武汉：武汉大学，2011.

Zhang Yunsheng.A multi－primitive and multi－view imagematching method based on self－adaptive triangle constraint［D］.Wuhan：Wuhan University，2011.

［4］ 丘文涛，赵建，刘杰.结合区域分割的SIFT图像匹配方法［J］.液晶与显示，2012，27（6）：827－831.

QIU Wen－tao，ZHAO Jian，LIU Jie.Image matching algrithm combining SIFT with region segmentation［J］.Chinese Journal of Crystals and Displays，2012，06：827－831.

［5］ Lowe D G.Distinctive image features frome scale－invariant keypoints［J］.International Journal of Computer vision，2004，6（2）：91－110.

［6］ Mikolajczyk K，Schmid C.A performance evaluation of local descriptors［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，2003，27（10）：1615－1630.

［7］ Harris C，Stephens M.A combined corner and edge detector［J］.In Proc.of Fourth Alvey Vision Conference，1988：147－151.

［8］ Brown M，Szeliski R，Winder S.Multi－image matching usingmulti－scale oriented patches［J］.Computer Vision and Pattern Recognition，Cvpr，IEEE Computer Society Conference on，2005，1：510－517.

A SIFT－based Trianglation Network Method for Image Matching

Guo Quanmin，Hu Xiaoxing
（School of Electronics and Information Engineer，Xi’an Technology University，Xi’an 710021，China）

Aiming at decreasing the high falsematching rate caused by scene complexity and serious disturbance lying in images matching，a method based on triangle constraint is proposed.It is a novel imagematching strategy based on SIFT（Scale Invariant Feature Transform）algorithm and uses the information of image structure.Themethod is separated into two steps.The first step is rough matching and good feature point is selected by applying SIFT and Harris algorithm to acquire distinctive feature point.The second step is elaboration matching，and the corresponding Delaunay triangulation network is established based on good feature points，and then SIFT is performed again to select feature points.Itwas verified that themethod improved the repetition and accuracy of featurematching.

SIFT Feature；Harris Feature；ANMS（Adaptive Non－Maximal Suppression）；Delaunay triangle；Feature extraction；Featurematching

10.3969/j.issn.1002－2279.2015.05.011

TP391

A

1002－2279（2015）05－0043－04

郭全民（1974－），男，陕西省渭南市人，副教授，主研方向：计算机测控技术。

胡晓星（1987－），女，河南新乡人，工程硕士，主研方向：图形图像处理。

2015－03－10