基于字典学习的残差信息融合图像去噪方法❋

董明堃，蒋爱民，孙 娟

（河海大学物联网工程学院，常州213022）

基于字典学习的残差信息融合图像去噪方法❋

董明堃，蒋爱民，孙 娟

（河海大学物联网工程学院，常州213022）

传统去噪算法只考虑从含噪图像中恢复出图像信息，然而对去噪后残差信号的利用却并未加以重视。针对图像去噪后残差信号中包含有用信息的特点，提出了一种基于字典学习的残差信息融合图像去噪方法。首先使用字典学习方法对单幅含噪图像进行去噪；然后对首次降噪后的残差图像进行图像块筛选；再对筛选出的图像块再次进行去噪处理；最后在小波域实现两幅图像的融合得到最终的去噪图像。实验结果表明，与传统基于字典学习的去噪方法相比，所提方法能够进一步提取残差信号中的图像特征信息，在峰值信噪比和结构相似度上都有所提升。特别是对一些细节较为复杂的场景图像，具有更好的去噪效果，从而证明了残差信号对于图像去噪的重要作用。

图像去噪；字典学习；图像残差；稀疏表示；小波融合

1 引 言

在许多图像应用领域中，人们需要高质量的清晰图像。然而在数字图像的获取和传输过程中，不可避免地受到噪声干扰，因此图像的去噪技术成为提升图像最终视觉质量最重要的步骤［1］。

人们通常将含噪图像表示为Y＝X＋N，其中Y表示含噪图像，X表示原始的清晰图像，N表示叠加在清晰图像之上的噪声。对于任意的含噪图像Y，去噪处理可以被看做为将Y分离成一个去噪图像＝ϑ1（Y）和残差图像E＝Y－ϑ1（Y）的过程。针对此种问题，人们一直在探索新的处理方法，逐渐形成了几个大的类别。一般来说，根据图像的表示方法不同，图像去噪方法可以大致归结为三类：空间域去噪、变换域去噪和字典学习去噪［2］。其中，空间域方法包括局部和非局部滤波，它们的主要区别在于滤波过程中所依据的筛选准则是空间距离约束还是相似性约束。变换域和字典学习方法主要是考虑将图像变换到其它域中。两者的不同点在于变换域使用固定的基函数去表示图像；而字典学习的方法则放弃了正交基函数，转而利用冗余字典表示图像信息。

自稀疏表示理论形成以来，它已被广泛用于各类图像处理任务之中。基于稀疏表示的去噪算法一般包含两部分：第一部分，利用含噪图像训练表示所需的冗余字典；第二部分，利用训练所得字典获取线性表示的系数，从而获得去噪结果。

一些研究者致力于分析不同噪声（如混合高斯噪声［3］，乘性噪声，高斯乘性混合噪声［4］）环境下的稀疏去噪算法。与此同时，另一些学者则更关注于稀疏去噪算法的运算结构优化与改进（如字典更新和学习的码字同步优化［5］、基于逐个原子更新学习过完备字典［6］等）。总之，以上这些研究的最终目的都是要解决含噪图像的去噪恢复问题。

在众多的基于稀疏表示的去噪算法中，最为典型的就是K－SVD去噪算法［7］。许多人结合其他思路对该方法进行了许多改进，以进一步提升其降噪效果，例如针对图像块间相关性结合非局部均值（Non－localmeans，NLM）的算法改进［8］等等。

一般情况下人们主要关注的是噪声去除方法的研究。更确切的说，是更加关注如何有效使用原始含噪图像以最大限度地提高去噪效果，但是忽略了残差信号中同样包含有原始图像信息。所提方法主要针对去噪后残差中所残留的信息进行提取，并与之前的重构图像进行融合，以进一步提升去噪效果。与此同时，对于所增加的计算量，提出的算法对运算结构进行了优化以提高运算速度。

2 基于字典学习的残差融合图像去噪方法基本思路

Dominique Brunet等人在2009年曾经对于图像去噪所得残差图像的用途进行过分析，对重构图像和其与原始含噪图像的残差进行了一系列测试，其中包括独立性测试、Pearson相关系数测试、G－test最大似然比显著性测试、K－S（Kolmogorov－Smirnov）测试等［9］。测试结果完全展现了残差与重构图像之间的相关性，以及其所含有的有用信息。为了实现去噪图像质量的进一步增强，需要对残差图像进行进一步的去噪以提取残留的图像信息。

所提出算法的计算结构可以表示成下式：

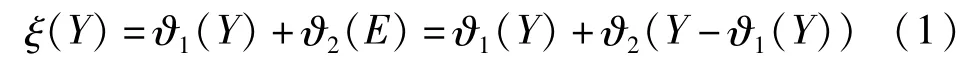
其中，Y表示原始含噪图像（如图1（a）），ϑ1（Y）指对原始含噪图像Y进行去噪处理后所得的图像（如图1（b）），残差图像E（如图1（c））是经过去噪处理ϑ1后所得的残差图像，即E＝Y－ϑ1（Y），ϑ2指针对残差E的信息提取或去噪处理，ξ（Y）即为最终合成的图像。对于原始含噪图像和残差图像的去噪重构（即ϑ1、ϑ2），均使用字典学习算法进行处理。

图1 去噪处理各阶段所对应图像示例

2.1 K－SVD算法去噪

在稀疏表示理论中，信号可以由冗余字典中原子的线性组合所表示。对于冗余字典，每个信号的表示并不唯一，因此实际中常常假设表示系数中含有大量的0，即信号可由字典中的原子稀疏表示。信号稀疏表示中的字典可以由各类固定基函数组合而成，但更为高效的方法是由信号训练出所需字典，这类字典更能很好地表征信号本质特征。因此，选择一个合适的字典学习算法是各类基于稀疏表示的去噪算法的关键。

给定一组信号yi，用其构成信号矩阵Y，则基于字典学习的去噪问题可以归结为如下形式：

这里的D∈Rs×n表示信号稀疏表示所需的冗余字典，dk表示字典中的第k个原子，μij表示拉格朗日乘子，Y为原始含噪图像，Rij用于从图像Y中提取第（i，j）个图像块，aij为图像中第（i，j）个图像块的稀疏表示系数。

为了解决上述问题，可以采用K－SVD字典学习算法提取去噪所需的冗余字典。该算法采用迭代方式不断更新字典中的原子和稀疏表示系数，每一次迭代包含以下两个主要步骤：

稀疏编码：使用已获得的初始字典，计算每个图像块的稀疏表示系数，该问题表示如下：

这里，C表示一个标量参数，σ表示图像噪声的标准差。对于式（3）所示的最优化问题，可以利用正交匹配追踪（Orthogonal matching pursuit algorithm，OMP）算法等稀疏编码算法求解。

字典更新：使用循环方式更新冗余字典D中每一个原子dk。对于需要更新的dk，原始优化问题可以表示为：

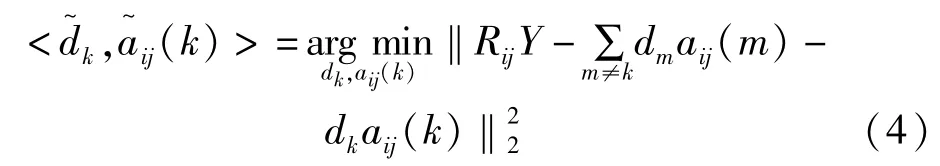
aij（m）表示系数矩阵的m行中的非零系数所组成的行向量。（4）式可以改写为：

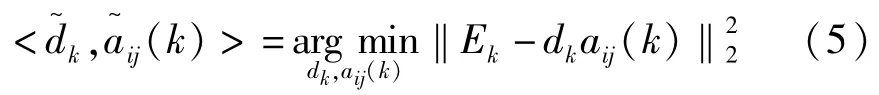
其中，

为了更新原子dk，对Ek进行奇异值（SVD）分解Ek＝UΔVT。这里，U和.V.均为酉矩阵，Δ是对角阵。不失一般性，假设所有奇异值按升序排列在对角线上。那么，U（：，1）即为最优解，Δ（1，1）V（：，1）即为稀疏表示系数的最优值（k）。

2.2 平行字典更新

使用K－SVD算法对含噪图像进行去噪处理，其主要缺点就是每次循环中均需进行奇异值分解，当信号维数较高时，所需计算量较大。为了减少计算规模，在K－SVD算法中的字典更新部分，提出使用平行原子更新字典学习（Parallel Atom－Updating Dictionary Learning，PAU－DL）的方法。考虑到总的残差矩阵，

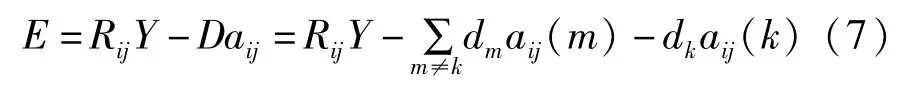
定义子矩阵Am＝dmaij（m），那么E可以分解为：

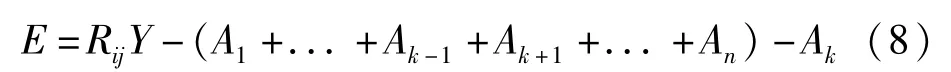
n为字典的原子数目，为了更新Ak，已经更新的A1，...，Ak－1被用于计算部分残差Ek，然而余下的子矩阵Ak＋1，...，An并没有被更新。为了解决残差矩阵每次迭代只有部分更新的问题，Mostafa提出了PAU－DL算法，对基于K－SVD的去噪过程进行运算结构的优化。为了更新每一个子矩阵Ak，需要计算部分残差矩阵Ek。可以看出此残差矩阵可以在迭代的运算过程中不断更新。首先使用给定字典D和稀疏系数aij计算总的残差E＝RijY－Daij。然后可以计算部分残差矩阵Ek＝E＋Ak，随后将第k个子矩阵Ak更新为，则残差矩阵被更新成E＝Ek－。如此便实现了K－SVD算法的一次迭代计算，且减少了迭代过程中的运算量。

2.3 基于相似度的残差图像截取

在对含噪图像使用PAU－DL算法进行去噪处理之后，含噪图像与去噪后图像间的残差中仍然保留着部分图像结构信息，例如原始图像的纹理、边缘信息等。这些信息可以从残差中提取出来，用于重构图像。由于在残差图像中所包含的噪声量远大于图像信息量，如果单纯使用PAU－DL算法对残差图像进行去噪处理，必将会引入大量噪声［10］，往往并不能取得很好的去噪效果。因此，在其后的处理中，探索利用残差图像与重构图像之间的相似性［11］进行进一步的去噪处理。

度量向量间的相似性有很多种方法，例如常用的欧几里得距离（Euclidean Distance）、曼哈顿距离（Manhattan Distance）、马氏距离（Mahalanobis Distance）、切比雪夫距离（Chebyshev Distance）以及向量空间余弦相似度（Cosine Similarity）等。由于几何中夹角余弦可以用来衡量两个向量的方向差异性［12］，考虑到图像块纹理的方向性特征，选择使用余弦相似度度量。对于重构图像和首次降噪后的残差图像，将两者的图像块转化为列向量，计算对应列向量之间的余弦相似度，

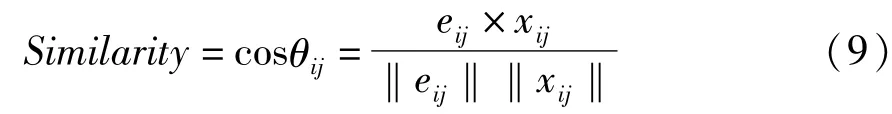
其中，eij表示由残差图像第（i，j）个图像块转化而来的列向量，xij表示由去噪后图像的第（i，j）个图像块转化而来的列向量。借鉴文献［12］中的思想，通过对夹角余弦设置一个阈值ε，

将残差图像块矩阵中那些不相似的图像块所对应的列向量置零，保留符合条件（10）的列向量，从而筛选出与重构图像相似度较高的图像块，将残差中占比重较大的噪声图像块直接滤除。利用这一方法筛选出的图像块所含有用信息较多，之后便可针对这些筛选出来的图像块进行单独的去噪处理。相较于直接使用残差图像进行信息提取，这种方法不仅大大减少了计算量，而且有效降低了大噪声对后续去噪处理的影响，进一步提升了去噪效果。

2.4 重构图像融合

在图像处理过程中，图像融合仍占有重要地位，其主要目的就是充分利用多个被融合图像中包含的冗余信息和互补信息，恢复图像。

借鉴基于小波分析的图像融合思想，所提出的方法使用小波分解方式处理降噪后的重构图像和基于残差相似块重构的图像，实现两幅图像的融合［13］。对此，可以采用Dauchies8小波对两幅重构图像进行变换，将其分解到不同的尺度上［14－15］。对于去噪后的残差图像而言，其高频部分含有较多的噪声信息，所以直接将其剔除，得到低频图像。将低频图像与的低频部分进行叠加，再与的高频部分进行小波逆变换，从而恢复出最终的去噪图像。综上所述，所提出的去噪算法基本流程如下：

输入：含噪图像Y。

输出：最终去噪图像。

（1）将DCT字典作为初始D，初始化残差字典D0，迭代次数J，迭代收敛阈值ε。

（2）含噪图像的去噪处理，迭代J次：

a.稀疏编码：给定D，利用稀疏编码算法求解稀疏表示系数。

b.字典学习：利用PAU－DL算法更新字典D。

3 实验与分析

为了验证所提出的去噪方法的性能，对各类图像进行了测试，测试所采用的图像为标准的512× 512灰度图像：Goldhill，Couple，Man和Bridge。图像中所添加的噪声满足高斯分布。对于每幅图像和每组参数，均进行10次独立的去噪处理，以验证算法的平均去噪效果。初次去噪时字典原子个数设置为256，后续处理中字典原子个数设置为128。经过一些测试，可以将式（10）中的阈值设置为0.001。实验中使用峰值信噪比（Peak Signal－to－Noise Ratio，PSNR）和结构相似度（Structural similarity index measurement，SSIM）这两个指标衡量去噪效果，它们分别定义为：

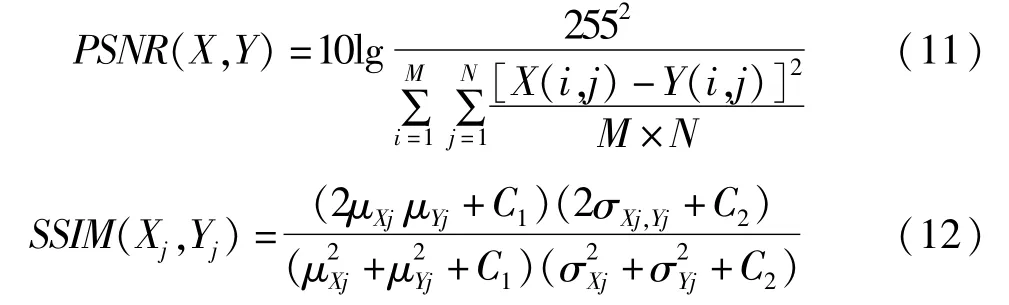
式中X和Y分别表示清洁图像和去噪后图像，X（i，j）和Y（i，j）表示相应位置的像素值，Xj和Yj表示相应的第j个图像块，μ和σ分别表示图像块的均值和标准差，M和N指两幅图像尺度，σXj，Yj表示两幅图像块的互相关，C1和C2表示正稳定性约束。

对于测试图像Boats进行去噪处理，结果如图2所示。

图2 残差去噪图像（σ＝20）

可以看出首次去噪后的残差图像包含有原始图像的一些有用信息，可用于进一步去噪处理。而基于残差所重构的图2（b）显示出类似于原始图像的结构。同时还对算法在不同噪声强度下的去噪性能进行了分析，对于每张测试图像，经过多次去噪测试，然后取数据均值，实验结果与K－SVD算法的去噪结果进行了对比，如表1所示。

测试结果表明，相比于K－SVD去噪算法，所提出的新方法能够提升绝大部分图像的去噪效果，具有较为广泛的应用价值。

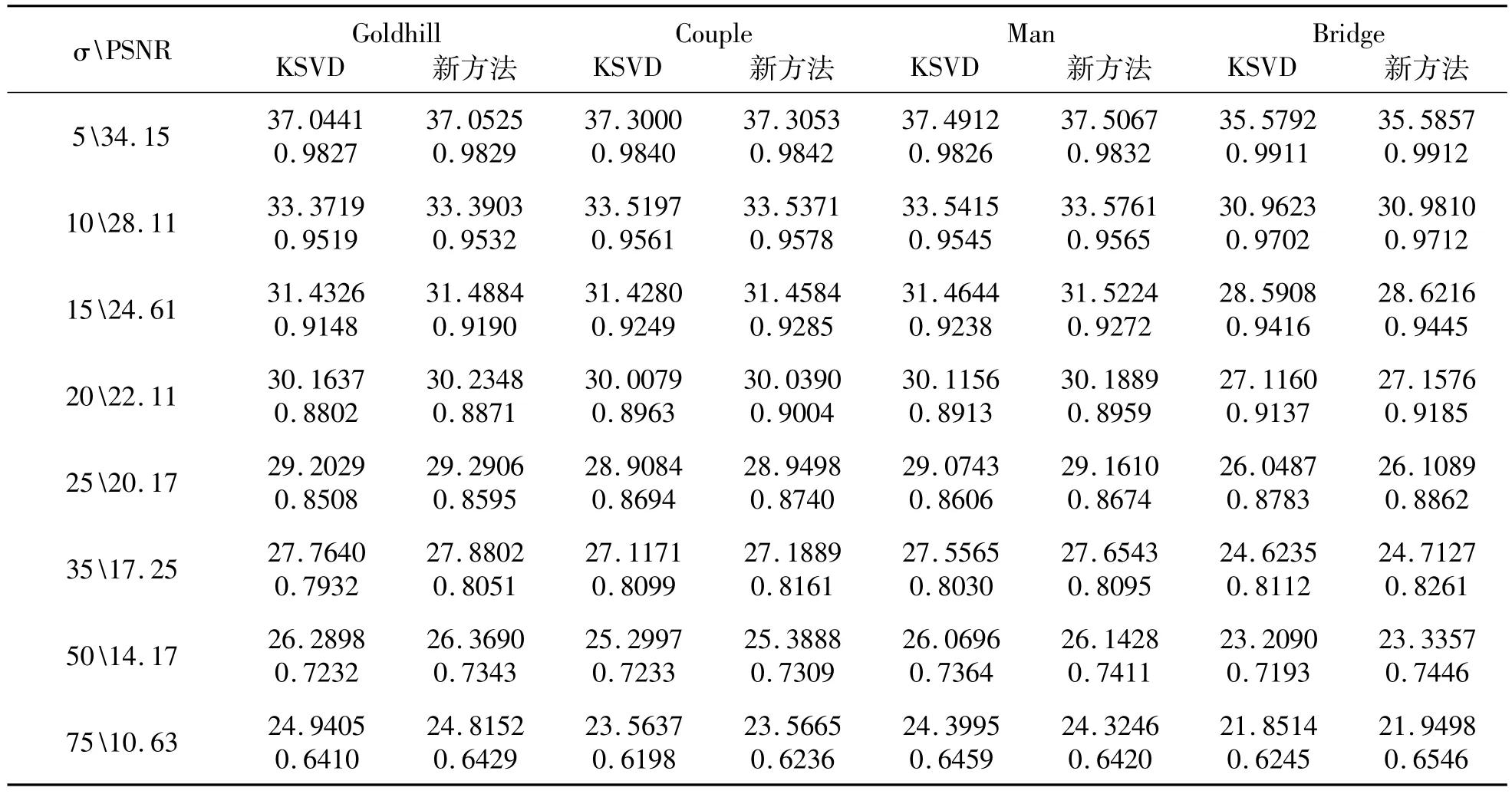
表1 与K－SVD去噪算法在不同图片和噪声水平下的去噪后PSNR和SSIM数据对比

4 结束语

针对图像降噪后残差信号中常常含有有用信息的特点，提出了一种基于字典学习的残差融合图像降噪方法。该方法首先利用PAU－DL算法构建图像的稀疏表示，然后再对首次降噪后的残差图像进行图像块筛选，从而将含有较大噪声的图像首先利用PAU－DL算法构建图像的稀疏表示，然后再对首次残差图像进行融合。实验表明，所提出的图像降噪的新方法对于结构性较为复杂的图像具有较好性能。

［1］ Elad M，Aharon M.Image denoising via sparse and representation over learned dictionaries［J］.IEEE Transactions on Image Processing，2006，15（12）：3736－3745.

［2］ Shao L，Yan R，Li X，et al.From heuristic optimization to dictionary learning：a review and comprehensive comparison of image denoising algorithms［J］.IEEE Transactions on Cybernetics，2013，44（7）：1001－1003.

［3］ Zhou Y，Ye Z，Xiao Y.A restoration algorithm for images contaminated by mixed gaussian plus random－valued impulse noise［J］.Journal of Visual Communication and Image Representation，2013，24（3）：283－294.

［4］ Liu J，Tai X C，Huang H，et al.A weighted dictionary learning model for denoising images corrupted by mixed noise［J］.IEEE Transactions on Image Processing，2013，22（3）：1108－1120.

［5］ DaiW，Xu T，Wang W.Simultaneous codeword optimization（SimCO）for dictionary update and learning［J］.IEEE Transactions on Signal Processing，2012，60（12）：6340－6353.

［6］ Sadeghi M，Babaie－Zadeh M，Jutten C.Learning overcomplete dictionaries based on atom－by－atom updating［J］.IEEE Transactions on Signal Processing，2014，62（4）：883－891.

［7］ Aharon M，Elad M，Bruckstein A M.The K－SVD：an algorithm for designing redundant dictionaries for sparse representation［J］.IEEE Transactions on Signal Processing，2006，54（11）：4311－4322.

［8］ 崔学英，张权，桂志国.基于字典学习的非局部均值去噪算法［J］.计算机应用，2013，33（5）：1420－1422.

［9］ Brunet D，Vrscay E R，Wang Z.The use of residuals in image denoising［C］.6th International Conference，Halifax，Canada：ICIAR，2009.

［10］ 张晓阳，柴毅，李华峰.基于K－SVD和残差比的低信噪比图像稀疏表示去噪［J］.光学技术，2012，38（1）：23－29.

［11］ Zhou W，Alan C B，Hamid R S，et al.Image quality assessment：from error visibility to structural similarity［J］.IEEE Transaction on Image Processing，2004，13（4）：600－612.

［12］ 何艳敏，甘涛，陈武凡.基于稀疏表示的两级图像去噪［J］.电子与信息学报，2012，34（9）：2268－2272.

［13］ Starck JL，Candès E J，Donoho D L.The curvelet transform for image denoising［J］.IEEE Transactions on Image Processing，2002，11（6）：670－684.

［14］ Liu Xiaoyan，Feng Xiangchu，Han Yu.Multi－scale non－localmeans for image denoising［C］.Proceedings of the 2013 International Conference on Wavelet Analysis and Pattern Recognition，Tianjin：ICWAPR，2013.

［15］ Shahan Nercessian，Karen A Panetta，Sos S Agaian.A multi－scale non－local means algorithm for image denoising［C］.Mobile Multimedia/Image Processing，Security，and Applications，Baltimore，Maryland，USA：SPIE，2012.

Dictionary－Learning－Based Image Denoising Method Using Information Fusion of Residuals

Dong Mingkun，Jiang Aimin，Sun Juan
（College of Internet of Things Engineering，Hohai University，Changzhou 213022，China）

The traditional image denoising algorithms focus on how to restore image information，but it pays less attention to the effects of residual signals obtained after denoising.Since residual signals contain the useful information，a dictionary－learning－based image denoising algorithm using information fusion of residuals is proposed in this paper.This algorithm first applies the traditional dictionary－learning－based denoising approach on a noisy image.Then，some image patches are selected from the residual image obtained in the previous step.These image patches are further denoised.Finally，the denoised image obtained in the first step and the one attained by the residual image are fused in the wavelet domain.The experimental results show that，compared with traditional dictionary－learning－based denoising algorithms，the proposed approach can consequently extract feature information of images from the residual signals and improve denoising performance with respect to peak signal－tonoise ratio（PSNR）and structural similarity index measurement（SSIM）.The proposed algorithm is especially suitable to images containing complex scenario details and can achieve better denoising performance，which illustrates the important effects of residual signals for image denoising.

Image denoising；Dictionary learning；Image residuals；Sparse representation；Wavelet fusion

10.3969/j.issn.1002－2279.2015.01.017

TP391

A

1002－2279（2015）01－0058－05

国家自然科学基金（61101158）；中央高校基本科研业务费项目（2011B11214）

董明堃（1986－），男，安徽省淮北市人，硕士研究生，主研方向：数字图像处理。

2014－07－18