空调系统温度不确定性及干扰的灰色预测补偿控制
2015-08-07徐丽红丁卫华张军
徐丽红,丁卫华,张军
空调系统温度不确定性及干扰的灰色预测补偿控制
徐丽红,丁卫华,张军
中央空调常规控制方法是基于PID算法的DDC控制,而空调系统的控制对象——热工对象具有一些独特的特征:多种干扰的影响,导致空调负荷大范围波动;季节的不同,使空调系统具有多工况性;温湿度相关性,增加了温度控制的难度。因而,常规PID温度控制系统适应性差、鲁棒性弱,此外,温度参数具有很强的滞后性,而补偿温度对象滞后特性的Smith预估控制由于要求精确的对象模型,因而,在常规PID+Smith预估控制的温度控制系统中,温度参数经常出现超调和振荡。为此,将空调温度系统的不确定性、多工况性、时变性、多扰动等特性采用灰色预测补偿控制策略进行补偿控制。仿真及实际运行情况均表明,控制效果较好,控制精度明显提高。
空调;温度;灰色预测;灰色;不确定性
0 引言
目前我国建筑能耗消耗巨大,空调系统又是建筑中的能耗大户,其运行时间长、耗电功率大。而人类对生活、工作和学习环境的要求也在不断提高,进一步加剧了空调系统的能耗。因此,建筑空调系统的高能耗问题显著,其对环境和气候的影响日益突出,怎样尽可能的降低空调系统的巨大能耗以及提高能源的使用效率,已经成为一个亟需解决的问题,如果措施得当,有望大大降低能耗,既能取得显著的经济效益,又能产生良好的社会效益,意义重大。
中央空调系统属于复杂系统,常用的控制策略一般都是PID算法的DDC控制。而温度环境系统自身极其复杂,各类环境因素之间相互制约、相互影响。房间温度受外界环境温度、气流运动、阳光照射、湿度、室内人员状况、室内设备状况以及各类随机干扰等诸多复杂因素的影响,使中央空调温度系统具有很强的不确定性,导致温度参数具有较强的非线性、时变性、耦合性、不精确性等。此外,温度参数的长延时、大滞后、多扰动等特点,同时,加剧了温度参数的控制难度。基于PID算法的常规DDC控制,在房间温度控制中效果不佳,温度波动大[1-4]。
本文采用灰色估计理论,将温度系统的不确定性和干扰进行灰色预测补偿。该研究方法在不必得到房间空气环境精确的数学模型、不必精确测量干扰的情况下,取得了较好的控制效果。
1 空调房间的数学模型
空调系统的作用是维持空调房间的温度和湿度在生产工艺要求或人体舒适性要求的范围之内。空调房间是空调系统的被控对象。
根据能量守恒定律,可以得到:
房间内蓄热量的变化率
=单位时间空调向房间输入的热量
+单位时间进入空调的显热量
+单位时间通过围护结构由房间外传入房间的热量
+单位时间室内设备、照明、人员的散热量
-单位时间从空调房间排出空气的显热量。
依据上述能量关系,经过一系列的推导[5],得到公式(1):

式(1)中:
C1:房间热容量系数;
θa:房间空气温度;
r:蒸汽气化潜热;
q:单位时间进入房间蒸汽量;
Gs:房间空气体积;
ρ:空气比热;
θ4:建筑物围护结构的温度;
θ’0:蒸汽受热之前空气的温度;
Q2:房间内设备;照明和人产生的热量;
Q4:建筑物围护结构所传递的热量;
R:房间内表面的热阻。
按照文献[5]所介绍的方法,经过若干步骤的推理,可以得到房间的数学模型如公式(2):

空调房间的传递函数(2)包含3个参数:
(1)增益 K1
增益 K1 是房间温度减低1度所需要的冷量;
(2)时间常数 T1
时间常数 T1 反应被控变量受干扰时达到新的平衡所需时间;
(3)延迟时间 τ
根据上述空调房间的分析和建模过程,建立组合式空调的简化数学模型;由于风机盘管的热传递具有延迟特性,组合式空调的传递函数如公式(3):
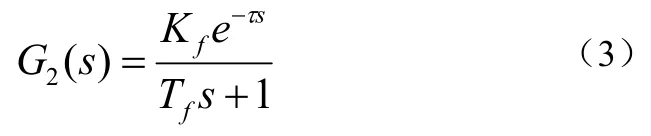
观察公式(2)和(3),可以发现,房间模型与组合式空调的模型均为一阶惯性环节+纯滞后。但现实中,空调房间是一个复杂的热力系统,很难用精确的数学模型来描述。在上述数学模型的建立过程中,隐含着如下的忽略或简化处理的方式:
(1)忽略内部空气流动和太阳辐射等因素的影响;
(2)假设被调房间的温度均匀分布;
(3)将外界环境的变化作为被控系统的扰动输入;
(4)忽略围护结构的蓄热量;
(5)将室温按集中参数来处理。
这部分内容在房间的数学模型中被忽略后,降低了模型建立和推导的难度,也降低了控制器的运算负担,但却增加了模型的不精确性和不确定性,导致控制精度降低、控制效果变差。然而,这种简化既是积极的、主动的,同时又是被动的,是不得已而为之,因为,这些因素本身就具备不确定性和不精确性,对其进行精确量测,在理论上和技术上都难以实现。在本研究工作中,这些在模型中被忽略掉的部分,将作为扰动和系统的不确定性部分,用灰色预测补偿算法进行处理。
2 空调系统不确定性及干扰的灰色预测
人们在研究事物的内在规律时经常会遇到不确定性问题。在处理不确定性问题时通常可以用概率论和数理统计或者模糊数学来解决。但是还有些不确定性问题不能用上述方式来解决,例如,人体内部参数。尽管人体的部分外部参数如体重、身高等,以及部分内部参数如血压、体温等是可以明确得到的,但人类生命活动的更多参数是未知的。这类不确定问题的特点是少数据、小样本、信息不完全和经验缺乏,这种现象,叫做灰性[7]。灰性的概念是“信息不确定”与“贫数据”两种概念的整合。不仅仅是人体,在更多的领域,如农业、工业、社会、经济等领域,由于运行机理不明确、条件繁多复杂、环境变化莫测、技术手段、处理手段有限等,大量的系统呈现灰性。这些灰性,大抵有如下几类:
① 运行机制灰性;
② 结构灰性;
③ 关系灰性;
④ 模型灰性;
⑤ 认知灰性。
温度控制系统正是符合灰性系统的特征。受控房间温度的变化受多个参数的影响,这些参数大多都呈现灰性,房间温度本身也呈现灰性特征。
本文在解决空调系统的温度这种不确定性问题中,为了使对象的灰量得到一定程度的白化,对空调系统的不确定部分建立灰色模型,并用特定的方法进行处理。仿真及实验数据表明,可以明显提高空调房间温度的控制性能以及控制系统的鲁棒性。
2.1 不确定性、干扰的灰色估计
用D(x,t)表征系统不确定部分及干扰,可用如下表达式描述如公式(4):
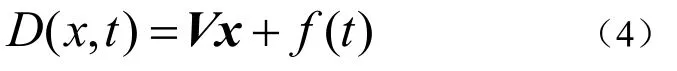
公式(4)中,

V是与系统状态有关的、但却无法准确确定或不能确定的部分。
f(t)是与系统状态无关的部分,比如各类干扰。
采用灰色系统理论中的生成算法,可以辨识出Vi,i=1,2,…,n,以及f(t),于是就得到了D(x,t)与x1,x2,…,xn的关系,从而估计出对应各状态的不确定量D(x,t)。
令x(0)为原始离散时间函数如公式(5):
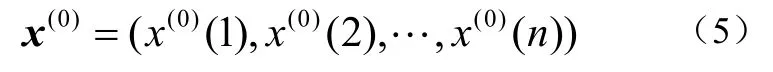
定义如公式(6):

称x(1)(k)为x(0)(k)的累加生成,表示为公式(7):

N个非线性不确定子系统构成的复合非线性不确定系统的状态方程如公式(8):
式(8)中,x∈Rn,u∈R,D(x,t)∈R ,A为n×n矩阵,b为n维列向量。bD(x,t)表示系统的不确定部分,包括参数不确定和外干扰等。D(x,t)无法直接测量得到,可根据测量数据按照间接计算得到如公式(9):
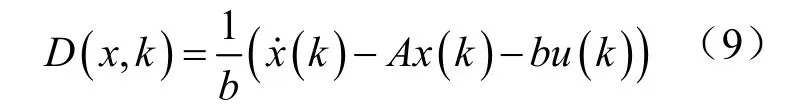
公式(9)中,D、x、b均为相应矩阵或向量中的某个对应元素。k=kT,T为采样周期。
不确定部分的灰色估计算法步骤如下:
i=1,2,…,n ,k=1,2,…N ,N≥n

② 计算的累加生成离散序列。其中,i、k、N的要求同①。
③ 计算B矩阵如公式(10):
式(10)中,BTB要求必须可逆。如果不可逆,则需要增加N,直到BTB可逆为止。
④ 根据x(0)(k)及式(9)、(10),计算D(0)(k)离散序列,其中,k=1,2,…N 。
⑤ 计算D(1)(k)的累加生成离散序列如公式(11):
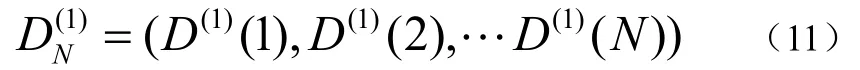
⑥ 计算不确定部分参数的估计值如公式(12):
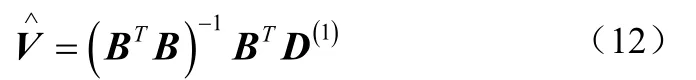
2.2 灰色补偿控制算法
PID算法是常用的一种控制算法,其不需要知道对象准确的数学模型,只需获得偏差信息即可实现控制,应用非常广泛,控制效果也很明显。但对于温度对象,因其具有大滞后和大惯性的特性,因而,行之有效的常规PID控制算法在温度对象的控制上却不能得到良好的效果。
Smith预估控制对于具有滞后特性对象的控制效果非常好,但Smith预估控制必须确切地知道对象的精确数学模型,才能建立准确的Smith预估模型来控制,否则,Smith预估控制同样不能奏效。
灰色补偿控制算法将空调系统的不确定性、不精确性、时变性、多扰动等特性,采用灰色预测补偿控制策略进行补偿控制,可以取得良好的控制效果。
灰色补偿控制算法如下:
① 采用任意一种闭环控制的方法,一般为P或PI或PID算法,对系统经过N次采样后,得到了N组数据,按照0节的方法,对不确定部分的模型参数V进行估计。
② 计算出估计参数后,由估计参数得到灰色补偿控制律如公式(13):
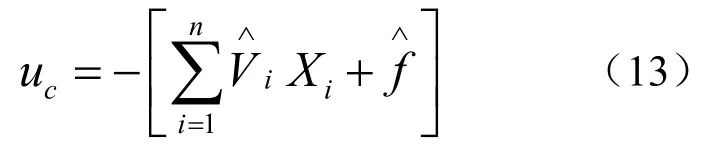
③ 按式(14)作为控制器的输出。其中,up为所采用的任意一种控制算法控制器输出如公式(14):

3 仿真结果及实际运行结果分析
为了验证上述灰色估计算法的可行性和有效性,首先,进行仿真试验。仿真模型和参数前已述及。
3.1 空调系统不确定性参数的灰色估计结果
由第1节所论述的建模方法以及试验房间的实测数据,得到该房间对象的相关参数为K=0.86,T=2700s,τ=450s。
为了验证0节所述算法的有效性,作者做了多组验证试验,试验数据如表1所示:

表1 不确定参数灰色估计结果
从表1可见,采用0节的算法,得到的灰色参量的估计值与其真值是非常接近的。表1中的试验数据表明了0节算法的有效性。
3.2 仿真结果分析
期望的温度变化规律如图1所示:

图1 期望的温度变化规律
房间初始时刻温度为32℃,该温度一直维持,直到第80分钟时,将温度设定为26℃。
在常规PID控制算法控制下的温度变化如图2所示:

图2 常规PID控制下的温度变化l
被控制量在振荡,无法稳定,谈不上控制精度。由此可见,常规PID控制算法无法解决房间温度变化的大滞后和长延时问题,因此引入Smith预估控制算法。
Smith预估控制下的温度变化情况如图3所示:
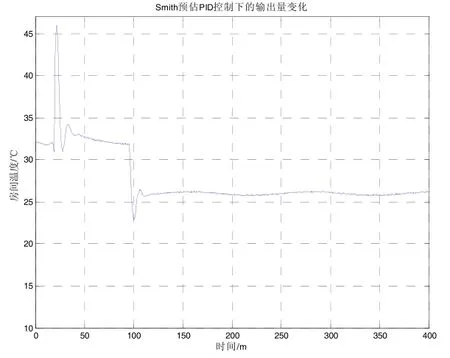
图3 Smith预估控制下的温度变化
可以看到,解决了常规PID控制算法下的温度一直振荡无法稳定的情况,静态精度也较高,温度可以维持在预先设定的32℃和26℃。但在输入温度值改变时,系统有很大的超调和几次振荡。从控制系统控制性能的角度来讲,说明Smith预估控制虽然解决了常规PID控制的温度振荡问题,并获得了很高的静态精度,但其动态性能却很不好,超调很大,有振荡。
系统不确定部分及干扰的灰色预测补偿控制下的温度变化如图4所示:
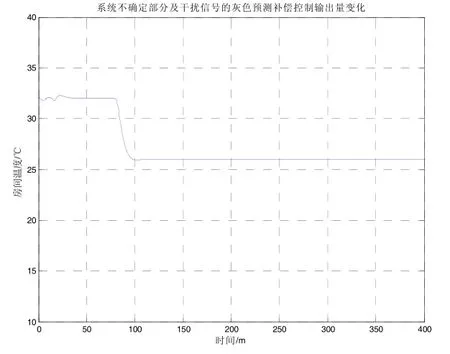
图4 系统不确定部分及干扰的灰色预测补偿控制下的温度变化
可以看到,控制效果比较满意,动态特性和静态特性均较好,能够满足期望的温度变化规律。温度变化基本没有超调和振荡。
为方便比较,以便更能直观的表达控制效果,将3种控制算法的控制仿真曲线放入同一张图中,如图5所示:
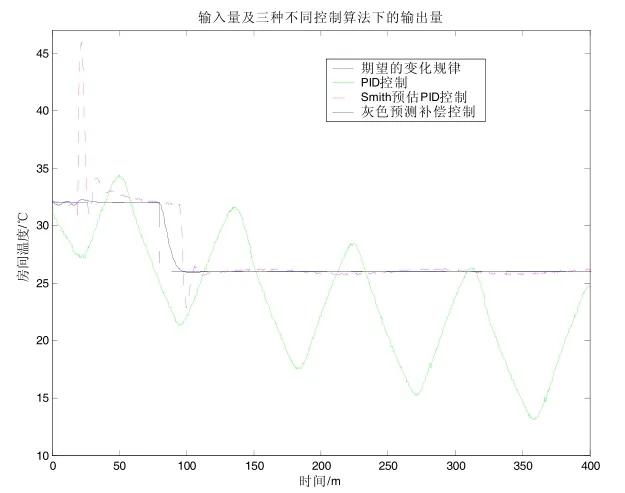
图5 三种控制算法仿真结果曲线
从仿真结果来看,将系统特性的不确定部分(灰色部分)及干扰用灰色补偿算法进行估计和预测,系统具有较快的响应速度,较高的控制精度,较小的超调量,控制效果明显优于Smith预估控制和常规PID控制,总体控制具有很大改善。那么,应用到实际系统中之后,控制效果又如何呢?
3.3 系统实际运行实测结果分析
从0节可知,系统不确定部分及干扰的灰色预测补偿控制具有很满意的控制性能,将其应用到空调房间进行实际运行测试。
试验过程中温度的实际变化过程记录及仿真温度曲线如图6所示:
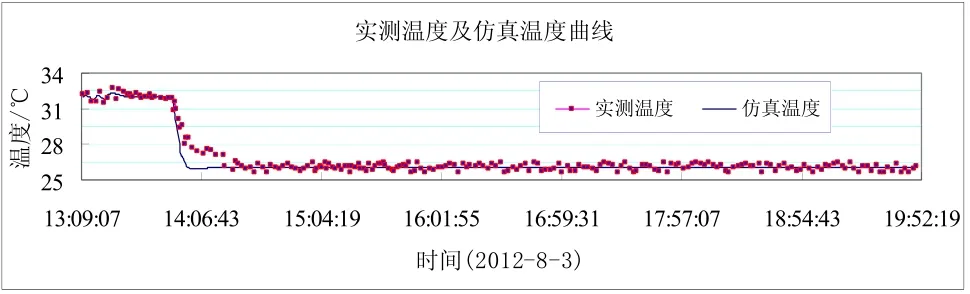
图6 空调系统不确定部分及干扰的灰色预测补偿控制下的实测温度变化曲线
可以看到,实测温度变化和温度仿真曲线吻合得非常好。这表明,本文提出的空调系统不确定部分及干扰的灰色预测补偿控制策略,其控制效果良好,可以达到预期目的。
4 总结
本文提出了利用灰色预测补偿控制算法将空调系统中不确定因素以及干扰进行估计和预测,使控制策略不再依赖于被控对象数学模型的精确获得及干扰的准确量测,避开了准确得到对象精确模型以及精确量测干扰这一困难。
仿真结果及系统的实际运行结果均表明,提出的控制策略是正确的和有效的。
[1]陆亚俊.暖通空调(第二版)[M].北京:中国建筑工业出版社,2007.
[2]Ang K H,Chong G. PID control system analysis,design,and technology[J].IEEE Transactions on Control System Technology,2005,13(4):559-576.
[3]Yun Li,Kiam Heong Ang,Gregor y C.Y.Chong. PID control system analysis and design[J]. IEEE Control System Magazine,2006(2).
[4]Xu TF,Carrie F R,Dickerhoff D J,et al.Performance of thermal distribution systems in large commercial buildings[J]. Energy and Buildings,2002,34(3):215-226.
[5]Zhangjun, Zhang Kanyu. An Improved Particle Swarm Optimization Approach for Temperature Control in HVAC for the Purpose of Energy Saving[J]. Trans Tech Publications, Switzerland, Advanced Materials Research 2012, 383-390:4768-4774.
[6]张军,张侃谕,周强. 基于改进模拟退火算法的多台冷水机组负荷优化分配[J].农业机械学报,2012,43(3):187-192.
[7]Julong Deng. The Primary Methods of Grey System Theory[M]. Wuhan: Huazhong University of Science & Technology Press.2005.
[8]Deng Julong. A novel GM(l,1) for non-equigap series.[J]The Journal of Grey System,1997(2):111-116.
[9]Juang Jih-Gau,Tu Kai-Ti1,Liu Wen-Kai1.Hybrid intelligent PID control for MIMO system[C]. 13th International Conference on Neural Information Processing, 2006: 654-663.
[10]Tuning the PID parameters for robot manipulators with compliant bases by using grey theory[C]. Lin J, Huang Z.-Z. Proceedings of the IEEE International Conference on Control Applications, 2007:2522-2527.
[11]张军,张侃谕.温室温度控制系统不确定性与干扰的灰色预测补偿算法[J].农业工程学报,2013,29(10):225-233.
Grey Prediction Compensation Control to the Uncertainty and Interference of the Air-conditioning System
Xu Lihong1, Ding Weihua2, Zhang Jun3
(1.Shanghai Technical Institute of Electronics & Information, Shanghai 201411, China; 2. Shanghai Institute of Aerospace Propulsion, Shanghai 201112, China; 3. Shanghai University of Electric Power, Shanghai 200090, China)
The conventional control method of central air-conditioner is the DCC control based on PID algorithm. But the control object of air-conditioner called thermal object has some unique characteristics such as wide fluctuation of the air-conditioner load caused by various disturbances, multi-operating conditions of the air-conditioner system caused by different season and difficulty of temperature control increased by the correlation between temperature and humidity. Therefore the conventional temperature control system based on PID has poor adaptation and robustness. Furthermore, the temperature parameters have large hysteresis and the Smith prediction control of hysteresis compensation to the temperature object requires accurate object model. So the overshoot and vibration of temperature parameters usually appear. For the purpose, it uses the grey prediction compensation control strategy to make compensation to the indeterminacy, multi-operating conditions, time-variation and multi-disturbance of the air-conditioner system. Both the simulation and actual operation indicate that the proposed control strategy achieves satisfactory results and the control accuracy is also significantly improved.
Air-conditioning System; Temperature; Grey Prediction; Grey; Uncertainty
TB66
A
2014.12.31)
1007-757X(2015)04-0058-04
徐丽红(1977-),女,辽宁沈阳人,上海电子信息职业技术学院,讲师,硕士研究生,研究方向:智能控制,机电一体化技术,上海,201411
丁卫华(1980-),男,山西晋城人,上海空间推进研究所,工程师,硕士研究生,研究方向:航天器热控制,上海,201411
张 军(1966-),男,内蒙古呼和浩特人,上海电力学院,副教授,博士,研究方向:智能控制与优化算法,综合节能,上海,201411
