基于回归分析法的某隧道围岩变形规律研究

陈映江，陈友生，穆成林

(成都理工大学 环境与土木工程学院，四川 成都 610059)

0 引 言

目前，我国的隧道工程大都以新奥法理论［1］为基本指导原则来进行结构设计和施工，该理论是将围岩看成黏弹塑性连续介质，根据围岩的位移变化的稳定性设计隧道的支护结构［2］，而隧道形状应对围岩受力有利，在充分发挥围岩自身承能力的同时，同时抑制围岩强度的恶化.同时，隧道开挖后，对现场位变数据进行采集，通过建立隧道的数值模型来研究围岩实际变形规律.对此，本研究在对围岩变形监测数据处理中运用回归分析法，通过对收敛变形量的预判分析，判断围岩变形的走势，并据此判断围岩的稳定情况.

1 函数模型及回归分析

对观测数据进行回归分析，可以很好地得出隧道围岩变形与时间的关系.当隧道掘进开挖时，其最终的收敛量总是趋于一个数值［3］，常用的隧道回归分析函数模型主要有:指数函数，u = Ae－B/t;对数函数，u = A+B/(lg(1 +t));双曲线函数，u = A/(A+Bt).本研究取对数函数作为回归分析因子模型，在指数函数中引入辅助变量，y = lnu;x = 1/t，可以将对数函数转化为，

利用最小二乘法原理，使得目标函数最小为“优化判据"，

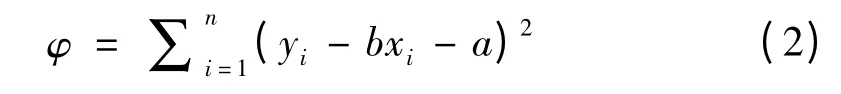
则满足条件为，

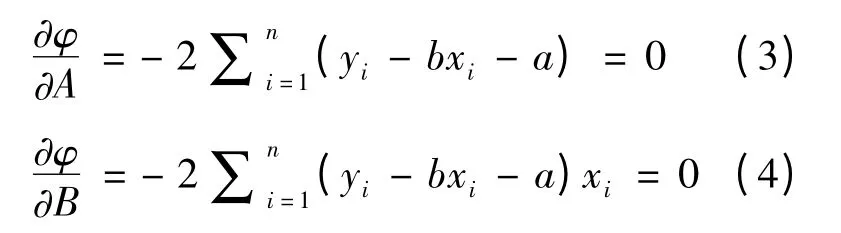
由式(2)、(3)可知回归系数a、b 分别为，

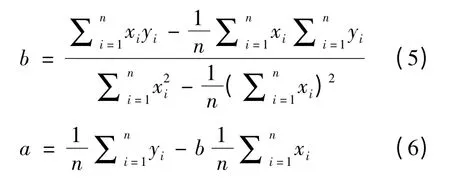
最后，将A = ea、B =－b 系数带入式(1)得到回归方程.

2 工程实例应用

2.1 隧道概况

高尔寺隧道位于四川甘孜境内，雅江县城以东约35 km 的高尔寺山.本隧道为单洞双向行车的特长越岭公路隧道，主洞内轮廓拟定为拱高650 cm，上半圆半径为R=490 cm 的三心圆曲边墙结构，其净空面积(含仰拱)64.27 m2，周长(含仰拱)29.12 m，其结构如图1 所示.

本研究以隧道D2 合同段ZK12 +930 断面为参考对象，该断面围岩等级为Ⅳ级、千枚岩、结构破碎，每组节理平均间距为0.2 ～0.4 S/m.边墙位移量测和拱顶下沉量测布置在同一量测断面(见图2)，其中点3 为拱顶下沉观测点.边墙位移量测正值表示洞周收敛，负值表示洞周扩张.在开挖后隧道后，隧道拱顶下沉与边墙现场量测数据如表1 所示.

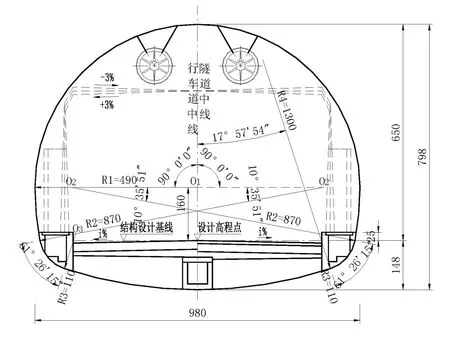
图1 主洞内轮廓设计图(带仰拱)

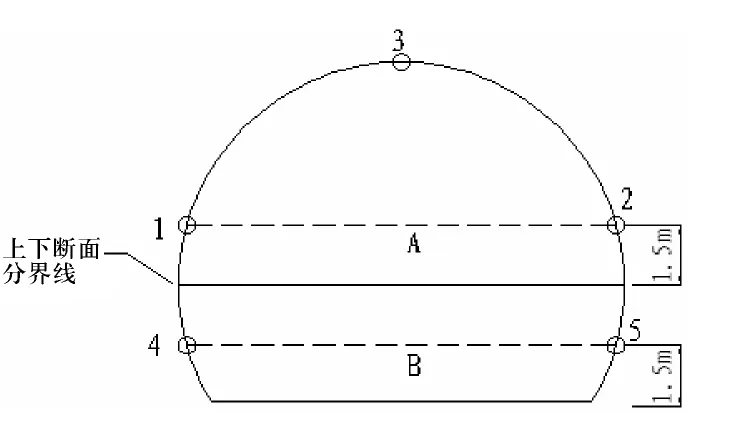
图2 观测点布置示意图

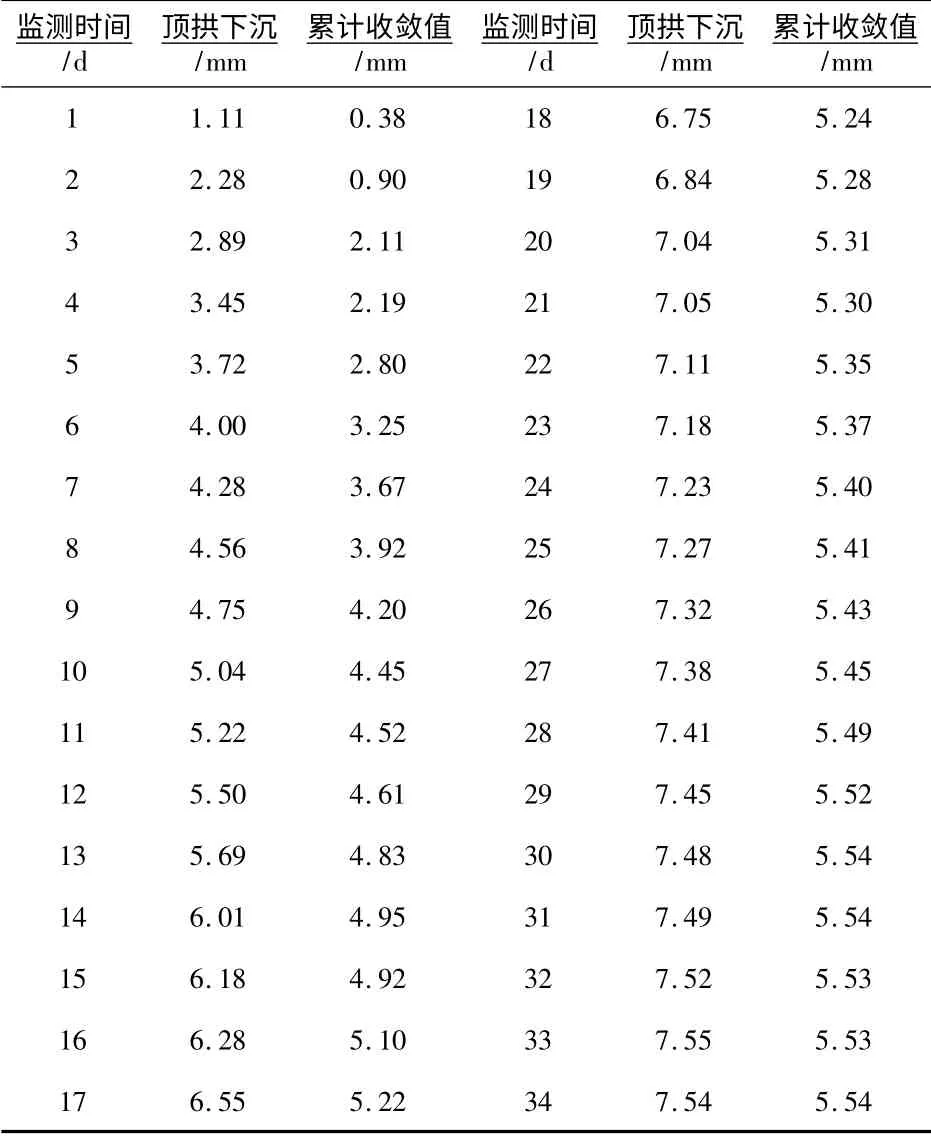
表1 断面拱顶下沉和边界累计收敛实测值

由式(5)、(6)计算可知，使得断面ZK12 +930拱顶沉降和边墙累计收敛位移量测数据最优需满足的条件是，A =7.9261，B =2.8860 和A =6.3172，B=3.7516，相应的围岩变形量的回归方程为，

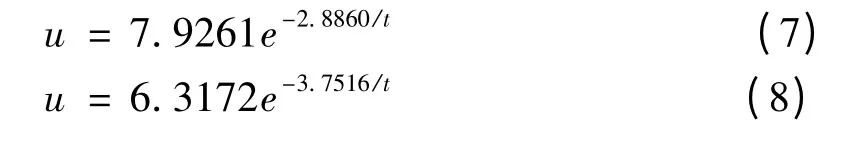
根据回归方程可计算出拱顶及边墙累计收敛回归值，表2 为断面误差检验表.

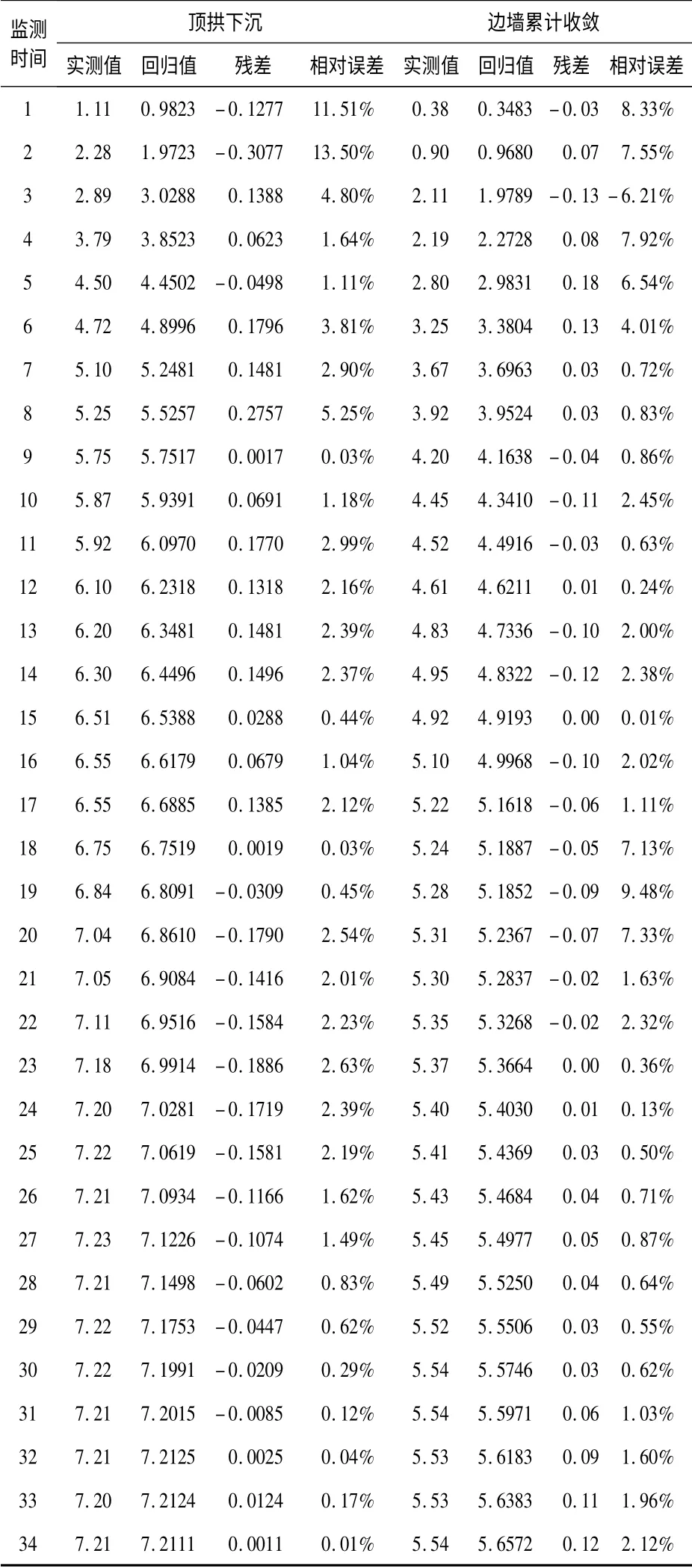
表2 断面误差检验表

2.2 精度分析

就具体工程应用而言，回归分析模型必须经过多方面的检验和判断后，才能够被用于实际工程预测，而常用的检验模型主要为，关联度合格模型和均方差比合格模型.模型的方差比值C 越小越好，表明残差比较集中，振动幅度较小，原始数据比较集中，摆动幅度大;而关联度ε 越大越好.

1)方差比值C.

原始数列X0，均值，，其方差，残 差 序 列，=其方差，则，

由式(9)计算断面拱顶下沉及边墙累计收敛回归模型的均方差为:

①拱顶下沉均方差比为，C = 0.084，

②边墙累计收敛均方差比为，C = 0.056.

据此判断，该精度等级为一级.

2)关联度ε.

设原始，X0= (x0(1)，x0(2)，…，x0(n)，Xi=(xi(1)，xi(2)，…，xi(n)，而…，(n)和分别为X0与Xi的始点化像，即，x0i(k)= xi(k)－ xi(1)，记，

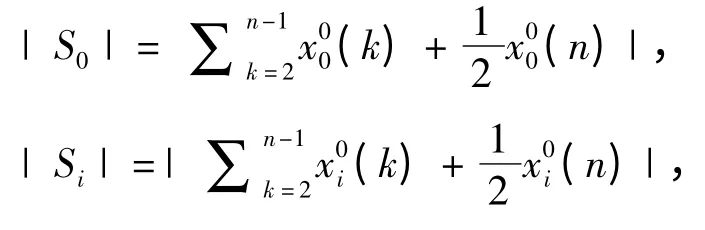
则称，

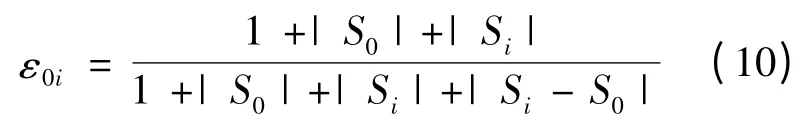
为X0与Xi的绝对关联度.

由式(10)计算断面拱顶下沉及边墙累计收敛回归模型的绝对相关度为:

①拱顶下沉相关度为，ε = 0.9908，

②边墙累计收敛相关度为，ε = 0.9959.

据此判断，该精度等级为一级.

综上所述，该随道断面的拱顶沉降回归模型和边墙累计收敛回归模型均能较好地反映隧道开挖后围岩位移随时间变化关系，结果如图3 所示.

3 结 论

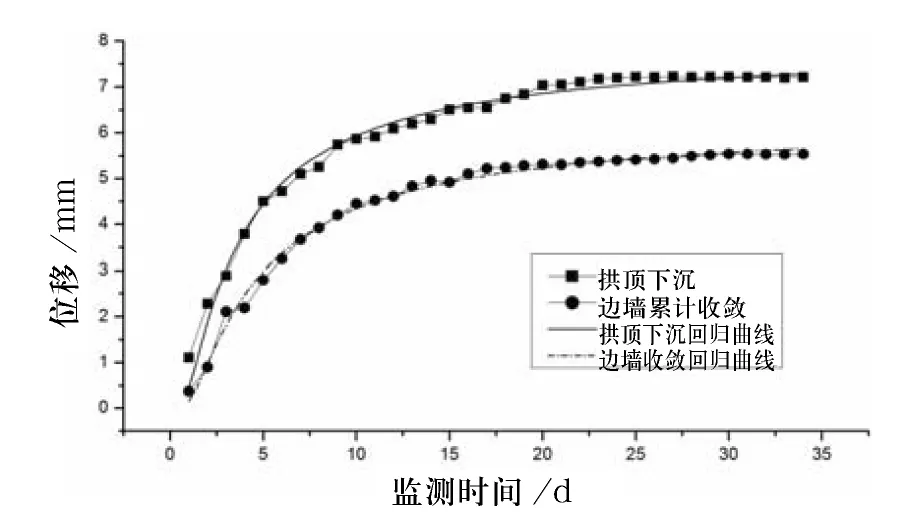
图3 实测位移值与计算位移值的对比

通过对隧道围岩开挖一段时间内的变形位移监测数据进行最小二乘法回归拟合计算分析与研究表明，拟合曲线与实际监测数据较为一致，采用的计算分析方法能科学地反映隧道围岩位移—时间变化规律.拱顶下沉以及边墙收敛位移值在开挖后8 ～10 d内变形速率较大，其后变形速率明显变小，25 ～35 d而逐渐趋于以稳定值.通过监测以及回归拟合曲线数据表明，对于Ⅳ级围岩，在开挖30 d 后边墙收敛及拱顶下沉均已稳定.根据相关围岩稳定性判定依据［5］可进行二次衬砌施工.由实测结果可知拱顶下沉量约为边墙位移量的1.35 倍，拱顶下沉变化速度稳定较边墙位移快.这与隧道拱顶下沉量一般为边墙位移量的1 ～2 倍［6］的结论吻合.本研究结论对该隧道围岩下一阶段的施工及支护具有一定的参考价值和指导意义.

［1］李晓红.隧道新奥法及其量测技术［M］.北京:科学出版社，2002.

［2］王建秀，朱合华，唐益群.高速公路隧道跟踪监测及承载状况诊断［J］.土木工程学报，2005，38(2):110－114.

［3］段慧玲，张林.隧道监控量测结果的析［J］.山西建筑，2007，33(33):333－334.

［4］蒋廷臣，张勤，周立，等.基于小波方法的非线性回归模型研究［J］.测绘学报，2006，35(4):337－341.

［5］徐兮.分段回归在隧道沉降变形监测的应用研究［J］.测绘通报，2007，53(12):18－20.

［6］吕康成.隧道工程试验检测技术［M］.北京:人民交通出版社，2002.