具有相同反射函数的微分方程类

周 坚，赵士银

(宿迁学院 教师教育系，江苏 宿迁 223800)

0 引 言

众所周知，客观世界中物体的运动规律通常可归为研究时变微分系统，

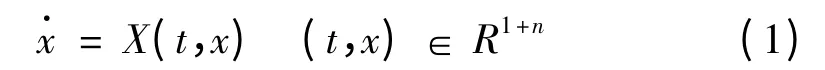
的解的性态.而在一般情况下，这并不是一件容易的事情.当系统(1)为周期系统时，即，

X(t +2ω，x)= X(t，x)，ω ＞0，

数学家Poincaré 和Lyapunov 提出了用变换法来研究该周期系统的解的性态，但对于有些周期系统，比如不可积系统，这种方法应用起来则非常困难.1981年，Mironenko［1－3］首先创建了反射函数理论，并借助反射函数这一最新工具来寻找周期系统(1)的Poincaré 映射，这为研究微分系统(1)，即使系统(1)为不可积系统，的解的几何性质提供了新的方法.在此基础上，周正新［4－7］对此作了深入研究，并取得了丰富的研究成果.结合反射函数的理论，可以看出不同的微分方程可能具有相同的反射函数，通过建立以同一个函数为反射函数的周期方程类，可以判断这些方程的周期解是否具有相同的几何性质.另外，为了探讨一些带扰动项的复杂微分方程的周期解的几何性质，只需研究与其等价的较简单微分方程的周期解的几何性质［8－9］.所以，微分方程的等价性对于研究一些复杂微分方程的解的性态具有非常重要的意义.

1 预备知识

定义1［3］称连续可微函数，F(t，x)= φ(－ t;t，x)，(t，x)∈D 为微分系统(1)的反射函数.由文献［3］知，可微函数F(t，x)∶D →Rn为微分系统(1)的反射函数当且仅当它为偏微分方程，

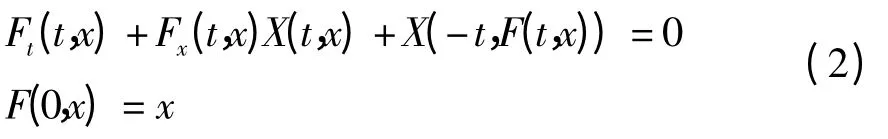
的解，称式(2)为关于反射函数的基本关系式.

引理1［3］(基本引理) 设微分系统(1)为关于t 的2ω-周期系统，F(t，x)为其反射函数，则系统(1)在［－ ω，ω］上的Poincaré 映射T(x)可以定义为，T(x)= F(－ ω，w)= φ(ω;－ ω，x)，从而系统(1)在［－ω，ω］上有定义的解，x(t)为2ω-周期解，当且仅当F(－ ω，x)= x.

定义2［3］若微分系统x·= Y(t，x)与微分系统(1)具有相同的反射函数，则称它们是等价的，具有相同反射函数的微分系统称为同一等价类.

引理2［3］若微分系统，

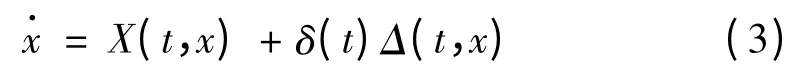
中，函数Δ(t，x)是偏微分方程，

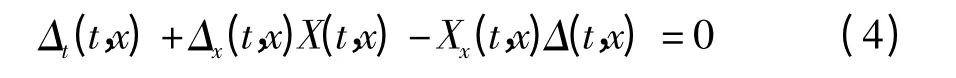
的解，则方程(3)和微分系统(1)等价，其中，δ(t)是任意连续奇函数.

引理3［3］若方程(3)和微分系统(1)等价，它们都为2ω-周期系统，则它们的Poincaré 映射相同，且它们在［－ ω，ω］上有定义的解x(t)为2ω-周期解，当且仅当，F(－ ω，x)= x.

2 主要定理

考虑分式微分方程，

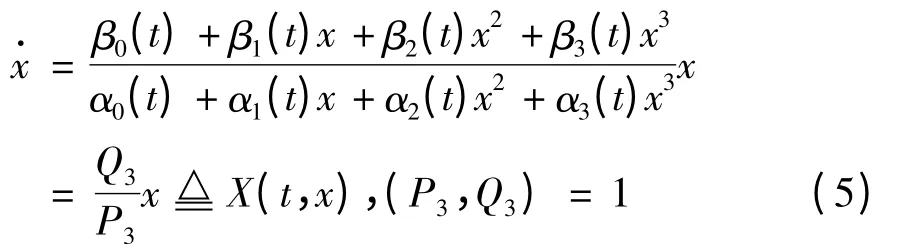
其中，αi(t)，βi(t)，(i = 0，1，2，3，t ∈R)连续可微，α0(t)α3(t)≠0.

为了讨论方便，简记，

定理1 若，

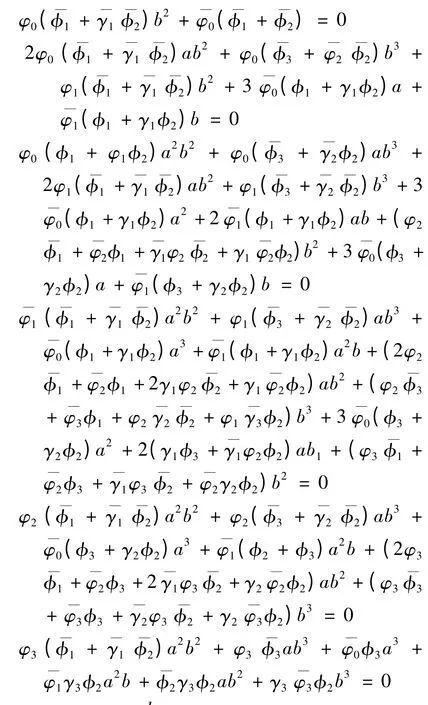
其中，

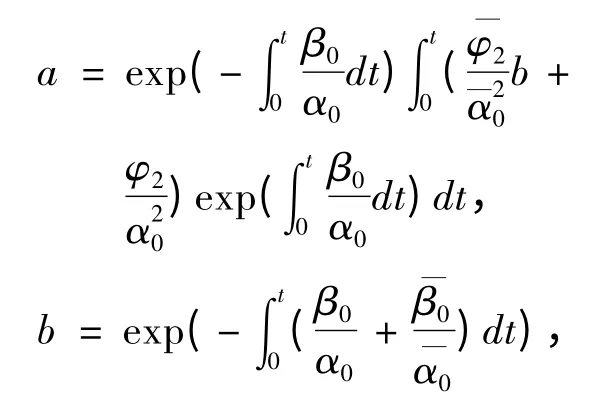
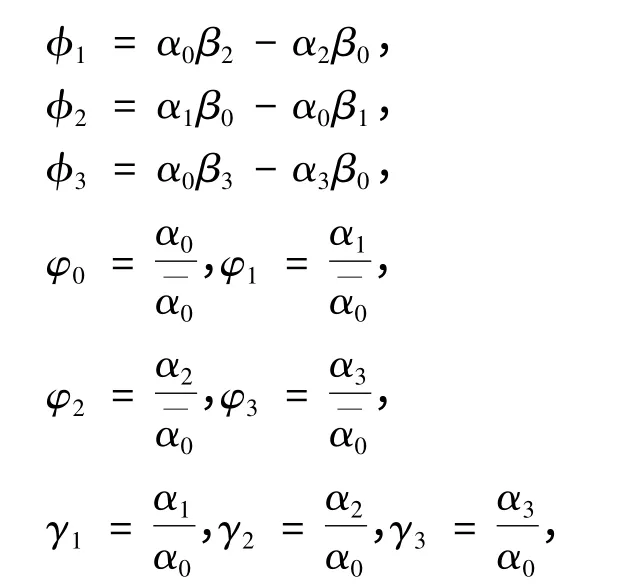
定理2 若定理1 的条件成立，且分式微分方程(5)为2ω-周期方程，则有，

①当a(－ ω)≠0 时，分式微分方程(5)存在2个2ω-周期解;

②当a(－ ω)= 0，b(－ ω)= 1 时，分式微分方程(5)存在无穷多个2ω-周期解;

③当a(－ ω)= 0，b(－ ω)≠1 时，分式微分方程(5)存在唯一一个2ω-周期解.

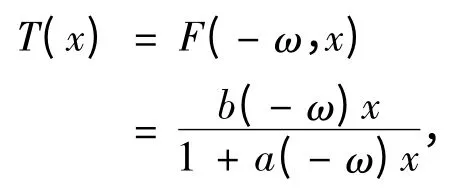
这样，由F(－ω，x)= x，即，(b(－ω)－1－a(－ω)x)= 0，可得到要证的结论.

例1 分式微分方程，

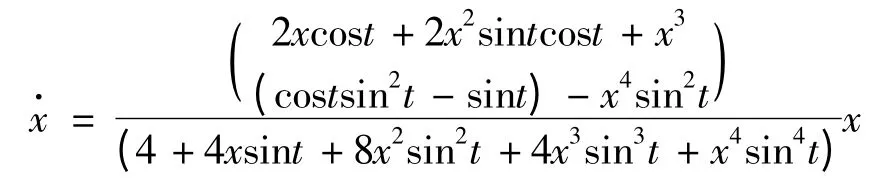
研究微分方程之间的等价性对于探讨某些复杂微分方程的周期解的几何性质具有重要意义，文献［5，8］已取得了一些很好的结果.在此基础上，本研究探讨当函数Δ(t，x)分别为，

Δ(t，x)= b0(t)+ b1(t)x + b2(t)x2，

与

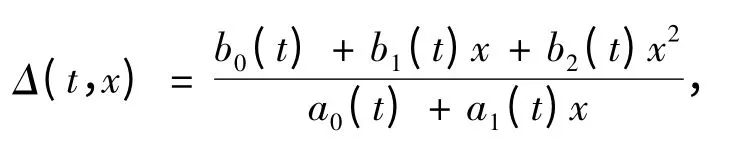
a0a1≠0 时，方程(3)与方程(5)之间的等价性.

定理3 若函数bi(t)，i = 0，1，2 满足以下条件:

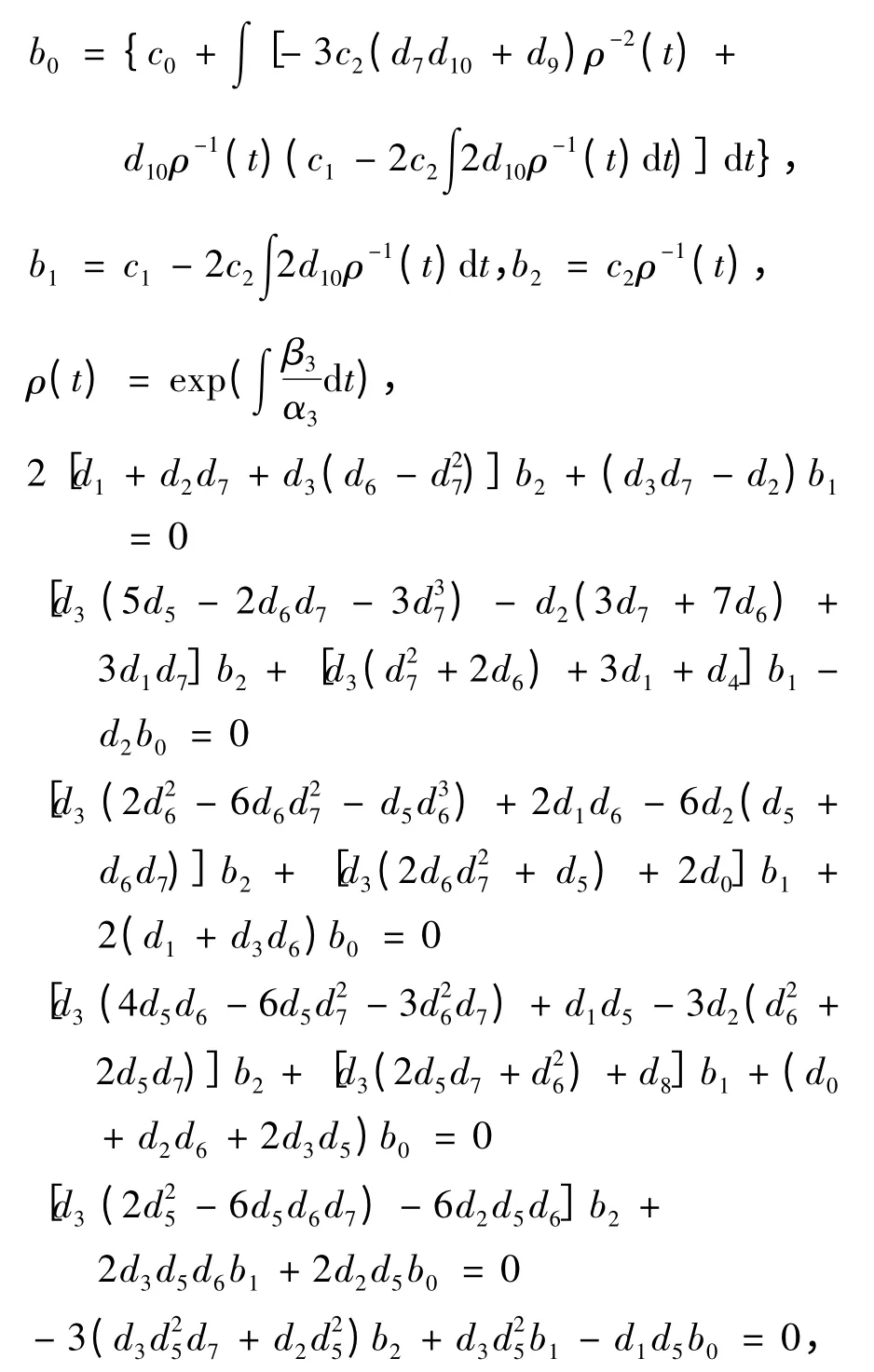
则当，Δ(t，x)= b0(t)+b1(t)x +b2(t)x2，bi(t)为连续可微的函数时，方程(3)与方程(5)等价.

其中，c0、c1、c2均为任意常数，d1= α3β0－α0β3，d2=α1β3－α3β1，d3= α2β3－α3β2，d4= α2β1－α1β2，di+5= αiα3，(i = 0，1，2)，d8= α1β0－ α0β1，d9=d2，d10= d3.

此外，若方程(3)与方程(5)的系数均为2ω-周期的，那么二者具有相同的Poincaré 映射，其周期解的性态也相同.

证明 将函数，Δ(t，x)= b0(t)+ b1(t)x +b2(t)x2代入关系式(4)并比较等式两端关于x 的同次幂的系数，即可推得定理结论.

同理可得.

定理4 设函数ai:= ai(t)，bj:= bj(t)，i = 0，1;j = 0，1，2，均连续可微且满足以下条件:

b2= ca1

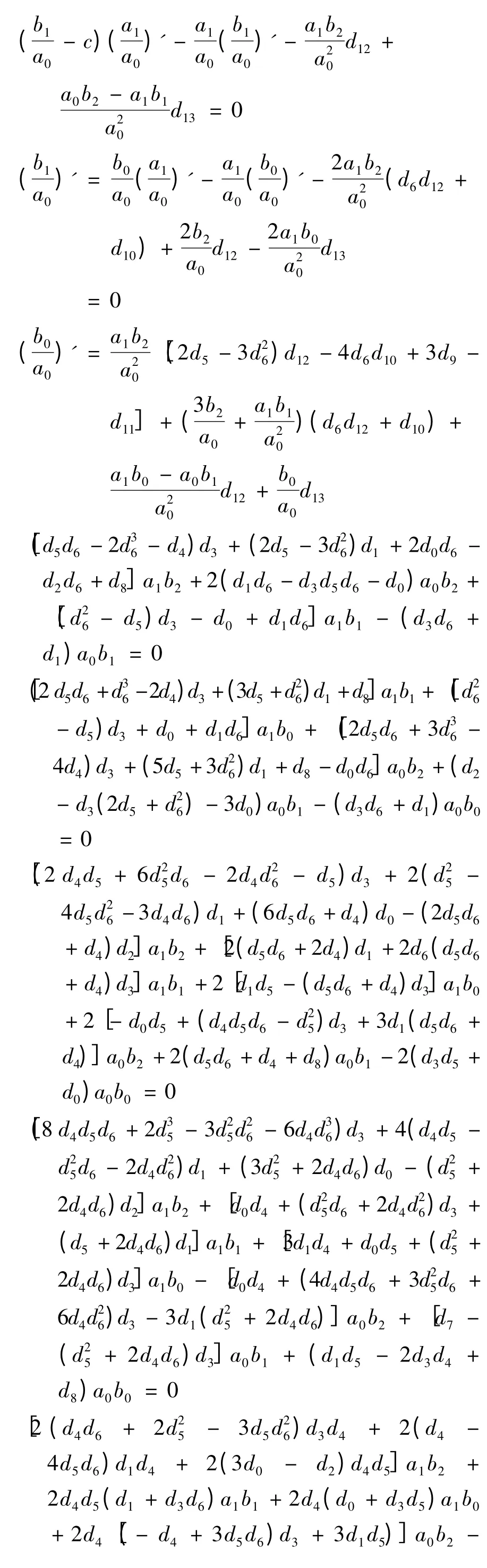
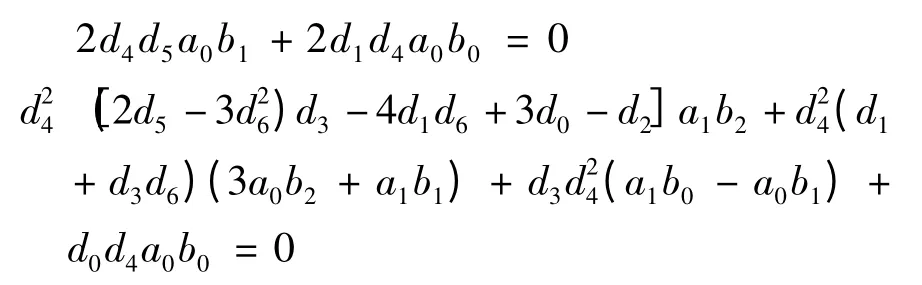
其中，d0= α0β3－α3β0，d1= α1β3－α3β1，d2= α2β1－α1β2，d3= α3β2－α2β3，di+4= αiα3，(i = 0，1，2)，d7= α1β0－α0β1，d8= α2β0－α0β2，d13= α3β3，dj+9= dj，(j = 0，1，2，3).

例2 分式微分方程，

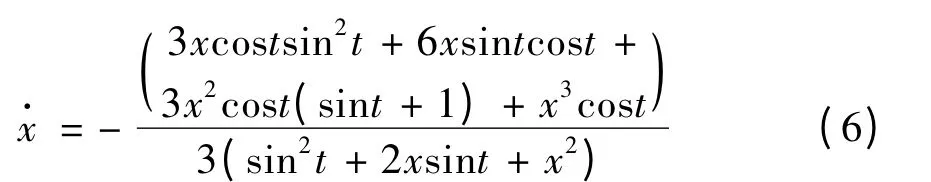
等价于，

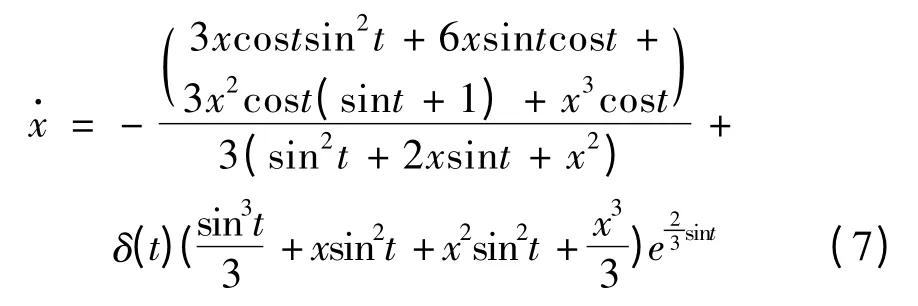
容易证出方程(6)具有反射函数F(t，x)=xesint.故方程(6)的Poincaré 映射可表示为T(x)=F(－ π，x)≡x.则方程(6)定义在［－ π，π］上的所有解都为2π-周期解.再由引理3 知，当δ(t)是以2π 为周期的连续可微奇函数时，方程(7)定义在［－π，π］上的所有解也为2π-周期解.

［1］Mironenko V I.Ordinary differential equation［M］.Moscow:Science Press，1971.

［2］Mironenko V I.On the method that allows one to determine the initial data of periodic solution of differential systems and to compare the mappings for a period［J］.Diff Eq，1980，14(11):1985－1994.

［3］Mironenko V I.Reflective function and periodic solution of the differential system［M］.Minsk:University Press，1986.

［4］Zhou Z X.The reflective function represented by three exponential matrixes［J］.Bull Kor Math Soc，2010，47(1):53－61.

［5］Zhou Z X.Equivalence of differential system［J］.Acta Math Appl Sin，2004，20(1):85－92.

［6］Zhou Z X.On the Poincaré mapping and period solutions of nonautonomous differential systems［J］.Pure Appl Ana，2007，60(2):541－547.

［7］Zhou Z X.On the relationship between quadratic polynomial differential system and the Bernoulli equation［J］.Appl Math Comp，2011，217(6):8716－8721.

［8］Zhou J.Differential systems with the same reflecting functions［J］.Appl Math Comp，2011，218(7):3144－3148.

［9］周坚.一类三次多项式微分系统的周期解［J］.应用数学，2014，27(2):426－432.