形态滤波与EEMD在振动筛轴承故障诊断中的应用
2015-07-31徐元博魏振东
徐元博,魏振东
(1.西京学院 机电技术系,西安 710123;2.华中科技大学 机械科学与工程学院,武汉 430074)
滚动轴承与其他机械零件的故障诊断有着较大的不同,轴承振动信号的频率范围很广,信噪比很低,有用信号在传递的同时能量衰减非常大,必须采用一些特殊的检测技术和信号提取方法才能得到故障特征信息。传统的Hilbert解调变换是轴承故障特征提取的常用办法,但其将高频调制信息与低频干扰和噪声分离时,对窄带滤波的选择有着较高的要求,而振动机械在运转时,不对中、不平衡等低频干扰现象和背景噪声更加强烈,相比于一般的旋转机械来说,信号传递更加复杂,信噪比更低,故障特征提取更加困难。
形态滤波法是基于积分几何和随机集的不同于时频域分析的方法[1],可以在滤除噪声的同时不改变故障信号的几何特征。因此,形态滤波已经运用到各个领域,在机械工程领域中,文献[2]将形态滤波成功运用到齿轮故障诊断当中,文献[3]利用形态滤波成功提取了旋转机械轴承故障特征。但形态滤波在抑制白噪声上的能力稍显不足,针对这一不足,可以利用集合平均经验分解(Ensemble Average Empirical Mode Decomposition, EEMD)算法对故障信号进行压缩和降噪,从而分离高频信息与低频干扰,并尝试将其应用于振动筛的轴承故障诊断中,通过试验验证了该方法的实用性。
1 数学形态学
1.1 数学形态学的基本变换
基于集合运算的数学形态学主要以集合代数、积分几何及拓扑为理论基础,提出了一套独特的变换或运算法则,为非线性信号处理提供了一种有效的方法。
形态学的运算构成比较简单,包括膨胀和腐蚀2种基本运算[4]。设f(n)和g(m)分别定义为F={0,1,2,…,N-1}和G={0,1,2,…,M-1}上的离散函数,且N≥M。f(n)为输入信号,g(m)为结构元素。则f(n)关于g(m)的腐蚀和膨胀分别定义为

(1)

(2)
式中:Θ和⊕分别表示腐蚀和膨胀运算。
f(n)关于g(n)的开运算和闭运算分别定义为
(f°g)(n)=(fΘg⊕g)(n),
(3)
(f·g)(n)=(f⊕gΘg)(n),
(4)
式中:°和·分别表示形态开和形态闭运算。
一般在运用上述两式时不单独进行开、闭运算,而是通常进行形态开、闭的级联形式。开-闭和闭-开组合形态滤波器定义为
(5)
式中:CO表示开-闭运算;OC表示闭-开运算。
1.2 结构元素的选取
结构元素的选取对信号的滤波消噪起着至关重要的作用,选取结构元素的一个重要原则就是要尽量选择与待分析信号的形态特征相一致的形状,一般只有与结构元素形状和尺寸相匹配的信号才能被保留[5]。
1.3 基于EEMD的形态滤波
如前所述,轴承故障信号的突出特征是冲击引起的高频共振,使故障特征信息被调制到高频段,且常常隐藏在低频谐波和噪声中[6]。因此该算法的核心思想为:首先利用EEMD算法把信号分解成一系列IMF分量,选取高频IMF分量进行重构;然后利用形态滤波对重构的高频故障信号进行消噪解调处理,去除故障信号中的噪声成分,在保持故障信号的形态特征的同时提高故障信号的信噪比;最后在此基础上,对滤波后的故障信号进行频谱分析,算法流程如图1所示。

图1 故障诊断流程图
2 仿真试验分析
构造3组机械源进行模拟仿真,各信号及复合故障信号的表达式为
y=x1(t)+x2(t)+10x3(t),
(7)
式中:x1(t)为假设的内圈故障,故障特征频率fic=100 Hz;fr为轴承旋转频率,即转子的1倍频率,fr= 30 Hz;x2(t)为转子不对中故障,f1x=30 Hz,f2x=60 Hz;x3(t)为背景噪声。模拟环境为强噪声背景环境,采样点数N=20 480,采样频率为1 000 Hz。
该复合故障信号的时频图如图2所示,频域图中出现了30 Hz和60 Hz的幅值,与转子不对中故障特征频率相对应,但轴承故障频率100 Hz淹没在强背景噪声中,并没有出现。

图2 复合故障信号的时频图
将图2a信号进行Hilbert解调变换,结果如图3所示,图中既没有出现转子不对中故障特征频率,也没有出现轴承故障特征频率,故障特征提取失败。

图3 Hilbert解调后的频谱图
将图2a信号进行EEMD处理后的结果如图4所示,将前3组能量较大的IMF分量重构后进行形态滤波解调,结果如图5所示。从图中可以看到形态滤波把轴承故障特征分离出来,说明该算法可以排除低频干扰和消除高频噪声。

图4 EEMD处理后的信号

图5 形态滤波解调后故障频谱图
3 应用实例
振动筛属于振动机械,其每个旋转轴上安装2个偏心块,当振动筛运行时,旋转轴带动偏心块一起旋转,从而产生离心力,这正是其与旋转机械运行工况的最大差别。另外,轴承与旋转轴之间存在间隙,离心力会使两者之间产生较大的径向力,从而紧密配合,增大摩擦力。由于内圈与旋转轴一起转动,使得径向力产生的包络区与点蚀区始终保持一定位置,即它们的相对位置保持不变,因此不会产生振幅调制现象,振动频率为nZfi(n=1,2,…),恰恰与旋转机械的内圈振动频率相反。因此,振动机械与旋转机械的内外圈频谱特征是相反的,振动机械的内圈特征与旋转机械的外圈特征相似,而外圈特征与内圈特征相似[7]。
试验轴承型号为1308型双列调心滚子轴承,轴承内径40 mm,外径90 mm,宽度23 mm,滚子数为15,接触角为30°。计算得轴承内、外圈故障特征频率分别为146.86和104.92 Hz。轴承点蚀深0.2 mm,长12.5 mm,其中内、外圈点蚀故障宽度分别为1.0 和0.7 mm,采样频率分别为20和100 kHz,采样点数为20 480,轴承转速为910 r/min(即工作频率为15.17 Hz)。
试验采用的振动筛如图6所示,振动筛为双轴惯性式激振,激振系统由偏心轴、偏心块、轴承、轴承座等装置组成,由2台功率相同的电动机带动,每个偏心轴的轴端各放置一个偏心块。偏心块使筛箱在离心力的作用下进行振动,因此可以通过改变偏心块的质量得到不同的振幅,同时可以通过单、双电动机的选择得到不同的振幅。试验共采用8块偏心块,其中4块为大偏心块,其余4块为小偏心块,分别进行单、双电动机试验,试验数组见表1。

图6 振动筛以及传感器布局图
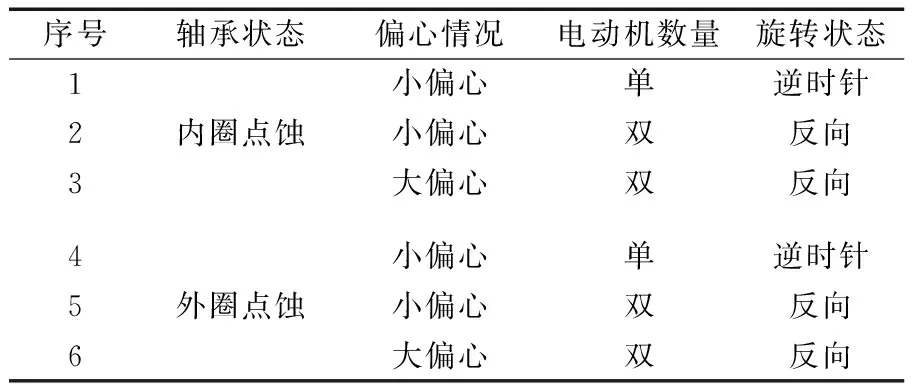
表1 试验数据表
因篇幅有限,选取内圈故障组的最小振动量级的1#和外圈故障组的最大振动量级的6#进行试验对比。振动筛轴承故障原始信号如图7所示。

图7 轴承故障原始信号
EEMD处理后的信号如图8所示,根据轴承故障信号的波形形态,结构元素选取三角形结构,经形态滤波解调后的频谱图如图9所示。而对原始故障信号直接进行Hilbert解调的结果如图10所示。

图8 EEMD处理后的故障信号

图9 形态滤波后的频谱图
对比图9和图10可以看出:在1#工况下,形态滤波和Hilbert解调变换都能把故障信号提取出来,但从图中可以看出特征频率的幅值相差很大,这是因为Hilbert解调变换后会损失一部分能量,而形态滤波在提取故障特征时损失能量很小;而在6#工况下,随着振动量级的增大以及背景噪声与其他干扰的增强,Hlibert解调变换方法对于故障特征提取效果明显下降,几乎看不到故障频率,说明Hilbert解调变换在强振动、背景噪声强烈的情况下进行故障特征提取能力有限,而形态滤波可以很好地进行故障特征的提取。
4 结束语
Hilbert解调变换对于轴承故障特征的提取可以起到一定的作用,但对于强噪声、高转速,特别是含有其他旋转件的特征信号时,有其局限性。通过振动筛轴承内、外圈故障特征提取试验,以及与传统Hilbert解调变换的对比,说明基于形态滤波的故障特征提取方法结合了EEMD算法和形态滤波算法的优点,克服了Hilbert解调变换中的一些缺点,能更好提取故障特征频率,更具有实用性。
