基于概率有限元法的大型LNG储罐可靠性评估及参数敏感性分析

2015-07-26陕西省天然气股份有限公司西安710016

山东工业技术 2015年1期

安　浩（陕西省天然气股份有限公司,　西安　710016）

安浩
（陕西省天然气股份有限公司,西安710016）

摘要：大型液化天然气储罐的安全性问题是一个十分重要的问题。因此，研究大型液化天然气储罐的可靠性评价方法具有重要的意义。本文以储罐结构的屈服强度为结构抗力，以球型罐体结构在负荷承载作用下所产生的最大应力叫做荷载效应，在建立大型液化天然气储罐正常使用极限状态的状态方程，由此得到大型液化天然气储罐可靠性的概率评价模型。最后，对某大型液化天然气储罐进行了可靠性及参数敏感性分析。实例说明了本文方法的有效性。

关键词：大型液化天然气储罐；安全性；可靠性；正常使用极限状态；参数敏感性

0　引言

当前我国已进入能源结构大幅调整的发展阶段，天然气以其环保、经济的优点越来越被广泛地使用。液化天然气(LiquefiedNaturalGas，简称LNG)储罐作为一种重要的能源存储设备在西方发达国家得到了广泛的应用[1]。LNG储罐在我国有着广阔的应用前景，我国建成、正在筹划或建设中的LNG储罐已有多处[1]。然而，大型LNG储罐的关键设计技术长期被西方发达国家垄断，我国的相关技术尚不成熟。众所周知，储罐是重大危险源，一旦发生有毒或易燃介质的泄露等事故不仅会带来大量经济损失，还会对生态环境造成严重的破坏。因此，开展大型LNG储罐安全可靠性设计与评价已迫在眉睫。为本文以现有可靠度理论为依据，建立大型LNG储罐的可靠性评价模型，提出了基于概率有限元的大型LNG储罐可靠性评价方法。该方法不仅可以给出大型LNG储罐的可靠概率，通过参数敏感性分析还可以揭示影响LNG储罐安全可靠性的主要因素，可为大型LNG储罐的可靠性设计提供参考和依据。

1　储罐可靠性的概率评价模型

但根据强度失效准则，储罐在使用过程中，不允许出现应力超过屈服强度的事件发生，如果应力超过屈服强度则认为结构失效。因此，可以以储罐结构的屈服强度是储罐结构具备的抗力R，以储罐结构在载荷承载作用下产生的最大应力作为作用效应S建立基于强度失效模式的储罐的功能函数如下：

由于储罐结构的作用效应是各基本随机变量的隐式函数，（1）式为隐式函数。

储罐结构的可靠概率Pf为：

2　基于概率有限元法的储罐结构可靠概率求解

由于LNG储罐的结构复杂，其结构结构响应量与随机变量间的函数关系也相当复杂，一般的高次非线性函数不能满足需求，其结构功能函数基本皆为隐式，这也要求采用新的求解方法计算其可靠度。对此，我们提出了一种基于概率有限元法进行解决。

2.1概率有限元法的基本方法原理

在杆系结构有限元理论概念中，结构刚度方程为：

（3）式中，H，u，f分别为刚度矩阵、节点位移列阵与节点荷载列阵。刚度矩阵是[2]：

（4）式中，B(X)、D(X,b)、u(b)、f(b)依次为应变矩阵、材料性能矩阵、节点位移矩阵和节点荷载矩阵。X几何坐标，积分域，D、u、f中b(x)是随机函数。

函数关系式中的物理量分解为随机变量的均值和偏差，有

将（5）式展开[2]：

（7）式可以看成是一个具有平均值的确定性有限元问题，和（3）式相同，只要把每个变量的平均值代入便可由有限元方程求得出结构节点位移的平均值。所以（8）式可以改写成:

因此，由（9）式可得出位移向量的协方差：

有限元分析中单元应力为

为了简便，可将B看成确定性矩阵，忽略二阶微量得应力均值和应力偏差为：

从(14)式可得各应力分量之间的协方差矩阵[2]：

概率有限元方程式（7）是位移均值控制方程，可以采用确定性有限元方程求解；（8）式是位移波动量控制方程。假设已知荷载波动量和刚度矩阵，把可看作为荷载项，用确定性有限元法去求解位移波动量。由（13）、（14）式求解出应力均值和波动量。

2.2统计模拟法（Monte -Car lo法）的基本原理

统计模拟法的基本原理为：在功能函数中随机抽取N个变量，然后分别将每个变量代入函数（）中进行验证，若计算结果记为有效，统计出有效个数L，当样本容量足够大时，以结构可靠的次数L占抽样总数N的频率来表示结构的可靠概率Pf，即。

2.3抽样方法的选择

直接抽样的Monte-Carlo法往往出现抽样数据点而导致仿真循环重复的现象，从而导致其计算效率低下，难以直接工程应用。

拉丁超立方抽样法在实际中应用较为广泛，其抽样原理可以解释为：假设随机变量的抽样次数为N；拉丁超立方抽样法是把每一次输入等概率地均分成N列子区间；对每一列子区间仅抽取1个样本即，每列中样本选取位置是随机的[3～6]。

不难看出，采用拉丁超立方抽样法选取的样本是离散的分布在空间中的，且具有记忆功能，从而很好的弥补了直接抽样法的不足。对比看来，拉丁超立方法的模拟次数能比直接抽样法少近40%[5，6]。根据以上原理，本文将对拉丁超立方抽样法和有限元相结合来求解结构的失效概率。

3　储罐可靠性分析

3.1工程概况及结构有限元分析模型

某球罐，球壳内直径为15700mm，厚度70mm。其材料弹性模量为2.094E5Mpa，泊松比为0.3，球罐屈服强度为235Mpa，工作压力为2.85Mpa，密度7.8E-6t/mm3。采用大型通用有限元软件ANSYS建模[7]，结构有限元模型如图1所示。

3.2 结构可靠性分析

可采用有限元分析软件（ansys软件）开展结构有限元分析，然后在编制球罐可靠性分析ANSYS参数化设计语言（APDL语言）程序。

3.2.1随机输入变量的确定

设球罐内直径D，壁厚T，工作压力P，屈服强度R，球罐密度DENSITY，材料弹性模量YOUNG，作为随机输入变量。随机输入变量的参数特征见表1。

表1　随机输入变量及参数特征表

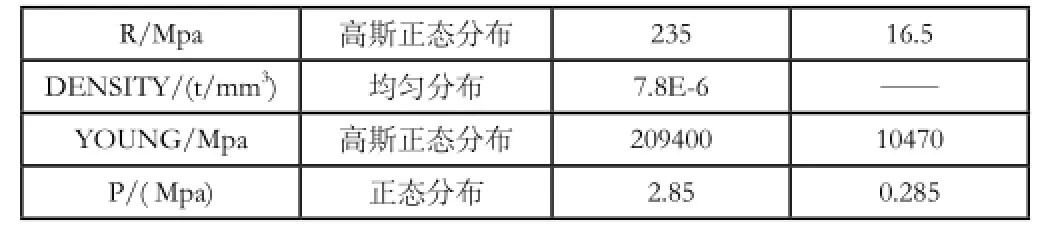
注 :密度 DENSITY服从均匀分布，Xmin=0.9×DENSITY，Xmax=1.1×DENSITY

3.2.2极限状态功能函数的确定

将表2中各随机变量带入球罐结构功能函数Z得到极限状态的球罐结构功能函数如下：

将球罐结构极限状态的响应量Z作为随机输出变量。

3.2.3抽样次数的确定

依照随机输入变量抽样的结果可以获得各种随机输入变量的频度图（概率密度函数图像）。举例展示，图2～5只列出部分随机输入变量抽样1000次得到的频度图。图6和图7分别为随机输出变量z的输出的样本均值历史和标准差历史。

由图2～5可以看出：各变量抽样得到的概率密度函数曲线与其分布类型相同，且与柱状图吻合较好[8]，光滑连续，表明抽样次数选择1000次较为合适。从图6、7可以看出，Z样本越趋近稳定状态，那么说明收敛带宽要越来越窄，而且空间特性的反映必须是在抽样次数足够的情况下。因此，本文采用拉丁超立方抽样法对各随机输入变量抽样1000次对球罐进行可靠性分析是合理的。

3.3可靠性分析结果及参数敏感性分析

3.3.1输出变量的概率分布

可将各随机输入变量套入功能函数可得到随机输出变量Z抽样过程状态图如图8。随机输出变量Z的概率分布和参数特征为见9和表2。

表2　输出参数的参数特征图表

由图8、9和表2可看出：输出变量Z均值大于0，表示储罐结构抗力总体上大于作用效应。同时也看出：输出变量Z的输出大致服从正态分布。

3.3.2球罐可靠概率

在置信度为95%时,结构的可靠概率为9.99455e-001（99.9455%）。

3.3.3参数敏感性分析

通过参数敏感性分析可以了各输入变量对球罐结构可靠性影响程度的大小，得到影响结构可靠性的主要因素。参数敏感性分析可以借助散点图和灵敏度分析来完成。笔者利用ansys软件的APDL语言提取各随机输入变量与输出变量Z的相关性散点图如图10～15所示。由各参数与输出变量Z的相关性散点图得到随机输入参数对输出变量Z的线性相关系数如表3所示。

表3　随机输入参数对输出变量的线性相关系数

从图10～15可以看出，随着球罐壁厚T，球罐屈服强度YIES，球罐弹性模量YOUNG等变量的加大，结构可靠概率增加。随着球罐结构的内直径D、压力LOAD的增大，球罐结构可靠概率会减小。

由图10～15还可直观地看出各随机输入变量与输出变量之间的关联性：球罐结构的屈服强度YIES与球罐可靠概率的相关性最强，压力LOAD次之，屈服强度YIES与压力LOAD是球罐可靠性的主要影响，对其可靠性起控制作用；而球罐结构的内直径D、球罐壁厚T、球罐弹性模量YOUNG等变量与球罐可靠概率相关性较小。也就是说，这些变量对球罐可靠概率的影响很小，是不显著项。

参数灵敏度分析如图16所展示。若输入参数对输出参数影响水平小于2.5%，表明为非明显影响因素，若影响水平大于2.5%，则表明为明显影响因素。从图16还可以看出，压力LOAD与屈服强度YIES是球罐结构可靠概率的明显影响因素，且屈服强度YIES的变异性对结构失效概率的影响大于压力LOAD。而球罐结构的内直径D、球罐壁厚T、球罐弹性模量YOUNG和密度DENSITY属于影响不大的非明显因素。

参数敏感性分析在球罐可靠性设计中非常重要，设计者往往都是根据参数敏感性分析的结果，找出影响储罐安全的主要因素，从而确保储罐结构的安全性。由以上的实例分析可以看出，屈服强度YIES、压力LOAD是影响球罐结构可靠概率的主要因素，可以通过选择高强度材料和减少压力的方式提升球罐的安全可靠性。

近些年来，大型液化天然气储罐在我国大量出现。储罐是重大危险源，研究储罐的安全可靠性具有重要的现实意义。本文首先建立储罐安全可靠性的概率评价模型，然后利用概率有限元法对某球型储罐进行了可靠性大小评价和参数敏感性分析。主要得到以下成果和结论：

（1）对于液化天然气储罐等大型复杂工程结构可靠性评价问题，因其结构功能函数的隐式性可采用概率有限元法来进行可靠性分析。

（2）通过强度失效准则，构建储罐结构的安全可靠性评价模型。通过实例分析说明该评价方法可以很好地得出影响储罐结构可靠概率的主要因素。从而可以为提高储罐结构的安全可靠性提供理论依据和有益参考。

参考文献：

[1]张斌．储罐基础沉降与变形后的可靠度评价研究[D].大庆：大庆石油学院,2007．

[2]金伟娅，张康达.可靠性工程[M].北京：化学工业出版社,2005.

[3]曾福强，朱燕军等.基于ANSYS概率有限元的薄壁高墩静风可靠性分析[J].中外公路,2011(03).

[4]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.

[5]王洁，武清玺.杆系结构蒙特卡罗法计算及敏感性分析[J].山西建筑,200632(03).

[6]张鹏.基于Kriging模型的隧道围岩稳定性分析[D].长沙：湖南大学硕士学位论文,2009(05).

[7]余伟炜等.ANSYS在机械与化工装备中的应用[M].北京:中国水利水电出版社,2005.