各向同性硬化参数对板料成形极限曲线计算结果的影响
2015-07-26上海交通大学材料科学与工程学院上海200240
夏 梦(上海交通大学材料科学与工程学院,上海200240)
各向同性硬化参数对板料成形极限曲线计算结果的影响
夏梦(上海交通大学材料科学与工程学院,上海200240)
摘要:板料的成形极限曲线可以通过材料的本构方程结合塑性失稳理论进行计算得到。本文使用了金属的弹塑性本构模型结合极限点分叉理论进行计算,研究了各向同性硬化指数n及强度系数k对金属材料的成形极限的影响。
关键词:各向同性硬化参数;成形极限曲线;塑性失稳理论
1 导论
板料的成形极限反映了它在加工达到塑性失稳前能获得的最大的变形程度,是板材成形的重要性能指标。1965年Keeler[1]及Goodwin[2]提出的以极限应变构成的成形极限曲线(FormingLimitCurve,FLC)为定量衡量板材拉伸失稳极限提供了一种简便实用的工具,至今仍广泛应用于板材成形领域。成形极限曲线可以通过试验测定和理论计算两种方法获得,其中理论计算主要是通过采用不同的屈服准则和塑性本构关系,利用拉伸失稳准则作为颈缩或断裂发生的判据来进行的[3]。随着有限元法及计算机技术的发展,板材成形极限图的理论计算更容易实现,其应用也更加广泛。
材料的应变硬化能力决定了材料在颈缩前依靠硬化使材料均匀变形的能力的大小,显然,材料的应变硬化参数对它的成形极限有着很大的影响。本文用弹塑性本构模型表征材料的力学行为,以极限点分叉理论作为颈缩发生的判据,使用ABAQUS进行了金属材料的成形极限曲线的预测计算,通过控制变量法研究了各向同性硬化指数n及强度参数k对成形极限曲线计算结果的影响。
2 材料的力学行为
计算使用的材料为弹塑性材料。当金属材料经历大变形时,其弹性变形远小于塑性变形,其力学行为一般采用次弹塑性模型来表征[4],次弹性响应定律为:
其中HY为一个标量模量,它与材料各向同性强化常数有关,Cep为四阶弹塑性切线模量的Voigt矩阵形式,a为表征加载方式的指数,当a=1时表示塑性加载,a=0表示弹性加载或卸载。
一般情况下,材料在断裂前内部组织会发生恶化,因此本文引入Lemaitre损伤理论提出的损伤标量d来表征金属材料中的微裂纹、孔隙等微损伤,变量d的定义为:
式中S、Sdef、Seff分别表示单位体积单元上某截面的面积、该截面的损伤面积及该截面的有效承载面积。在Lemaitre模型中,如果考虑微裂纹和微空洞的方向性,那么d就是法向量的函数,本文中假设损伤是各向同性的,即金属在各方向上微缺陷都是相同的,因此将损伤变量d作为标量考虑且取值区间为[0,1]。d等于0时表示单元完全无损伤,d等于1时表示单元完全受损分裂成两部分。
那么在此模型下材料某截面上的有效应力与名义应力之间则具有如下关系:
二者关系的物理解释为损伤系数为d的单位体积元某截面名义应力对应的应变等效于无损伤的单位体积元该截面上有效应力对应的应变。损伤参数d的演化方程为:
其中Hd为一个标量模量,与材料常数β、Sa、sb,弹性应变能释放率Ye及其阈值Yei有关。
使用式(6)新定义的有效应力取代公式(1)(2)(3)中的应力张量,经过推导可以得到新的应力率与总变形率之间的关系为:
式(5)与式(9)即为我们计算时使用的材料本构方程,计算时将以上本构关系通过UMAT用户子程序实现,程序中采用4阶龙格库塔算法来进行应力迭代更新。
3 Va lanis极限点分叉理论
极限点分叉理论是一种预测材料的分散性失稳的理论,最早由Valanis在1989年提出,所以又称为Valanis极限点分叉理论,它认为颈缩发生时名义应力是不变的,即有:
其中,N为名义应力张量,T为第一类P-K应力张量,F为变形梯度,Lt为连接变形梯度材料时间导数与第一类P-K应力率的切线模量,在使用以t时刻的当前时刻构形为参考构形的更新拉格朗日方法时它具有如下表达形式:
于是,颈缩发生时切线模量Lt是奇异的,必有一个特征值为0,在计算时当出现第一个为0的特征值时,此时det(Lt)=0,式(10)得到满足,此时程序停止计算,输出的长轴应变与短轴应变值即为该材料在该加载路径下的极限应变值。
4 计算结果
本文的计算分别在无损伤弹塑性材料模型和带损伤弹塑性模型下进行,材料服从第二节所述的本构关系和Ludw ig各向同性硬化准则,计算使用的主要材料参数如下表所示,其中的损伤参数只适用于带损伤模型。各向同性硬化模型硬化模型的两个重要参数分别为强度系数k和硬化指数n,下面将采用控制变量法来进行计算以研究这两个参数对材料成形极限的影响。当k取值变化时,n始终取值为0.6;同样地,当n取值变化时,k的取值始终为550MPa。计算结果如图1及图2所示。
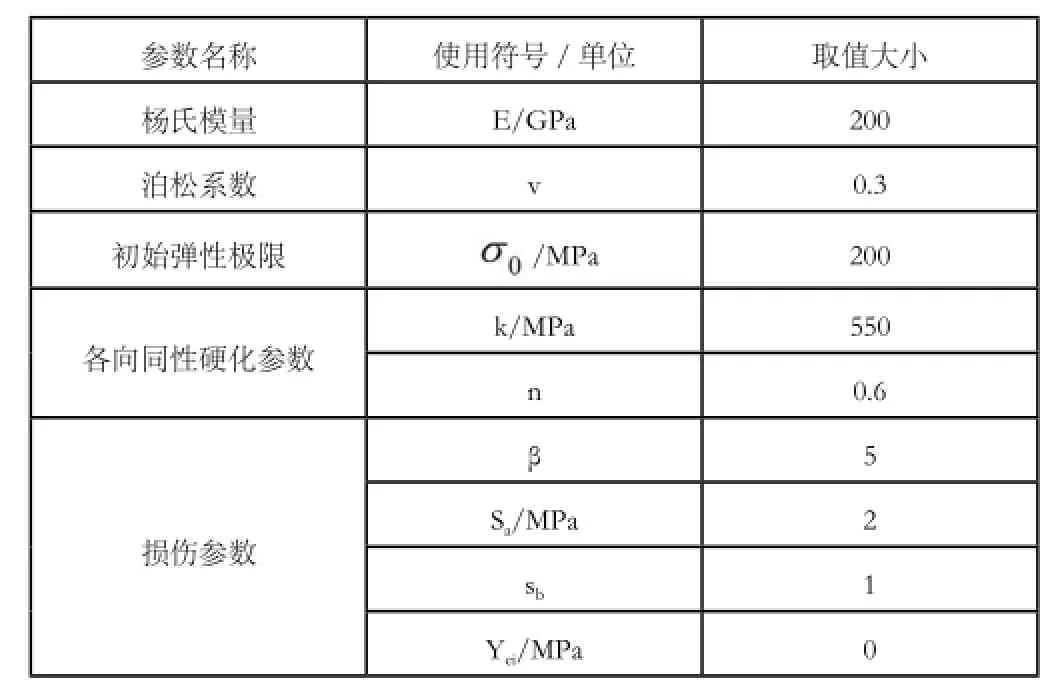
计算使用材料模型的主要参数
硬化指数n对FLCs的影响的计算结果如图1所示。结果显示,尽管损伤的演变改变了成形极限曲线的形状并降低了材料的成形极限,但n值的大小对材料成形极限的影响趋势都是相同的,即硬化指数值越大变形集中出现得越晚,板料的成形极限曲线越高,但是曲线的整体形状并不受其取值大小的影响。应变硬化指数n反映的是材料在颈缩失稳发生前依靠硬化进行均匀变形的能力,n值越高,材料由均匀变形到不均匀变形的转折点越往后推移。
图2显示了强度系数k对FLCs的影响。图2(a)显示出在不考虑损伤时,参数k的取值越大,材料的成形极限曲线的位置越高即材料的成形性能越好,但是这种影响并不是均匀的,可以看出k=1500MPa与k=1000MPa时的成形极限之间的差异要明显小于k=1000MPa与k=500MPa时的成形极限之间的差异。文献研究表明k值能反映材料的抗塑性变形能力、可承受均匀变形的最大程度以及实际的承载能力,因此可以作为一个衡量板料成形能力的指标。而图2(b)显示的结果则完全不同于图2(a)的结果,在材料存在损伤时,反而是应变强度系数k值越大,成形极限曲线越低,并且k值的改变还有可能影响成形极限曲线的形状,当k值从500MPa变为1000MPa时,成形极限曲线的形状发生了明显的变化,且在拉-压区成形极限之间的差异较小,而在拉-拉区成形极限之间存在明显的差异。造成这种差异的可能原因是:k值的不同会影响材料损伤发展的程度,当损伤发展带来的负面影响要高于k值增加带来的正面影响时就会出现如图2(b)所示的变化趋势。应变强化系数与损伤之间的关系还有待验证,但是显然k值对板料成形极限的影响并不是独立的,如何用它来准确衡量板料的成形极限还有待研究。
5 结论
本文使用金属材料的弹塑性本构模型,结合Valanis极限点分叉理论,使用ABAQUS软件对材料的成形极限曲线进行了理论计算,研究了各向同性硬化指数n和强度系数k对金属材料的成形极限曲线的理论预测值的影响,结果显示:n值越大,曲线越高即材料的成形性越好;在无损伤时,k值越大曲线越高,而在有损伤时,k值越大曲线越低,我们认为这是由于损伤带来的负面影响高于k值带来的正面影响造成的,可能与设定的损伤相关参数取值有关,具体关系有待进一步验证。
参考文献:
[1]Keeler,S.P.Determination of the forming limitsin automotive stamping[J]. Sheet Metal Industr ies,1965(42): 683-703.
[2]Goodwin, G.M..Application of the strain analysis to steel metal forming in press shop[J].La Metal lurgia Ital iana ,1968(08):767-772.
[3]陈劼实,周贤宾.板料成形极限的理论预测与数值模拟研究[J].塑性工程学报,2004,11(01):13-17.
[4]庄茁译.连续体和结构的非线性有限元[M].北京:清华大学出版社,2002:534-537.
作者简介:夏梦(1990-),女,硕士生,主要研究方向为金属薄板的成形性。
