基于预测电流控制的BLDCM转矩控制

周林阳，王生捷

(北京机械设备研究所，北京100854)

具有梯形反电动势的永磁无刷直流电机(brushless direct currentmotor，BLDCM)转矩脉动大的问题一直限制其在高精度伺服控制系统中的应用．为降低其转矩脉动，国内外的专家学者从各个方面做了大量的研究．文献［1－2］中对无刷直流电机的导通方式及换相转矩脉动做了详细研究:文献［1］对无刷直流电机的120°导通方式和180°导通方式的转矩脉动进行了比较，得出180°导通方式更适合于使用在高速场合中的结论;文献［2］提出在换相阶段采用180°导通方式，而在非换相阶段采用120°的导通方式的控制方法，对单一120°导通方式在换相期间，由非导通相续流造成的换相转矩脉动起到了明显的抑制作用．

也有学者将成功应用于异步电机和交流同步电机上的直接转矩控制(direct torque control，DTC)引入BLDCM控制系统中，在转矩脉动的抑制上取得了较好的效果［3－4］．文献［3］提出了可行的 BLDCMDTC方案，但是需要对转子磁链进行微分计算，转矩观测复杂;文献［4］采用离线构造反电动势函数，然后在实际运行中根据实时位置和速度计算出反电动势值，再由反电动势值和三相电流计算出转矩，避免了在转矩过程中微分量的计算，但是其采用的是120°的导通方式，由于关断相浮动电压的存在使得定子给定量计算困难．文献［5］采用180°的导通方式实现了BLDCM的直接自控制(direct self-control，DSC)，但是其存在较大的电流脉动，而且低速性能较差．文献［6］创造性地将超空间电压矢量的概念引入到定子三相绕组中坐标系中，采用120°导通方式，将电机运行过程中的关断相放置于垂直于另外两相的超空间坐标系中，使得定子磁链在非关断相所形成的平面中的投影为正六边形，从而实现了六边形磁链的直接自控制(DSC)，成功地解决了电流脉动大的问题，取得较好的控制效果．以上的4种BLDCM控制方法都遵循DTC或DSC控制的基本原理，需要实时检测定子磁链，并与定子磁链给定值做比较，然后利用滞环控制器产生逆变器导通与关断信号，然而定子磁链观测不准确同样也会造成转矩脉动．文献［7］省去磁链观测环节，实现了BLDCM的无磁链观测器直接转矩控制，这种直接转矩控制虽然简单，但是从其控制结果上看，电流脉动较大．预测控制目前在电机控制中也得到广泛应用，文献［8］对预测控制在电机控制系统中的应用做了广泛的研究，提出了预测电流控制方法，但是对转矩控制没有涉及．文献［9］则采用预测电流控制实现了对永磁同步电机的控制，取得了较好的控制效果．

文中提出适用于BLDCM的基于120°导通模式的预测电流控制及基于混合导通模式的预测电流控制两种方案，对电机的电流、转速及转矩起到较好的控制作用．

1 BLDCM数学模型

假设具有梯形反电动势的永磁无刷直流电机，三相绕组为Y形连接，表贴式永磁体，忽略磁路饱和、涡流等影响，则电机在Oabc坐标系中的电压平衡方程可以表示［1］为

式中:un，in，en分别为三相绕组的电压、电流及反电动势;R为绕组的电阻;L为绕组的电感;p为微分算子．

记 ωr为转子速度为转子磁链的导数，则电机转子磁链导数与反电动势之间存在以下关系:

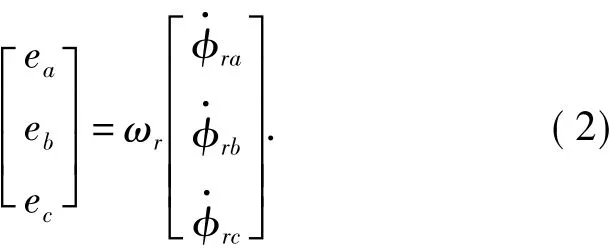
再记Pn为转子磁极数，则电机的电磁转矩Te可以表示［6］为

在永磁同步电动机直接转矩控制系统中，为了方便分析，除了使用三相绕组的abc坐标系外，通常还会用到αβO以及dqO坐标系．其中αβO坐标系为静止坐标系，其定义为:α轴与Oabc坐标系的a轴重合，β轴超前α轴90°．从αβO坐标系到Oabc坐标系之间的转换矩阵为

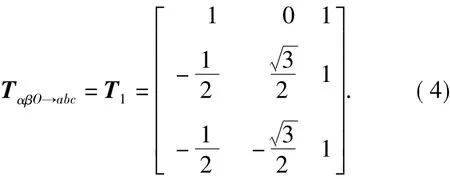
dqO坐标系为旋转坐标系，d轴与转子轴线重合，q轴超前d轴90°，整个坐标系随转子同步旋转，如果记转子与α轴(a轴)之间的角度为θe，则从dqO坐标系到αβO坐标系之间的转换矩阵为

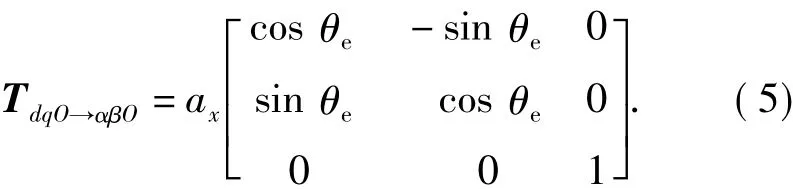
由于同步电机的反电动势为正弦波，在转换到dqO 坐标系之后，可以将的值转换为 0［1］，从很大程度上方便了转矩的分析．但对于具有梯形反电动势的无刷直流电机的值不为 0，dqO 坐标系不再适用．

为此文献［9］提出一种扩展的dqO坐标系，记为dxqxO坐标系，其与abc坐标系及αβO坐标系之间的空间关系如图1所示．

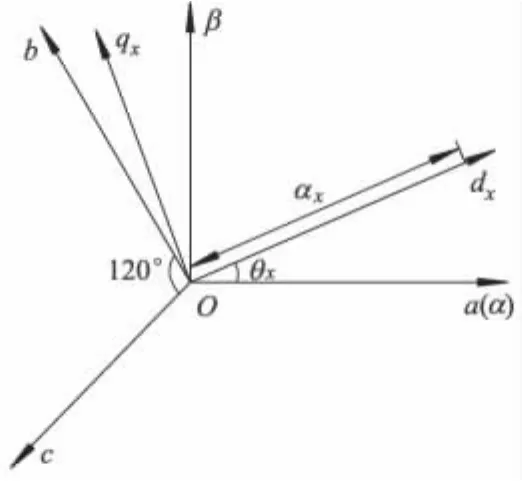
图1 3个坐标系之间的空间关系

由图1可知，3个坐标系之间的转换矩阵为

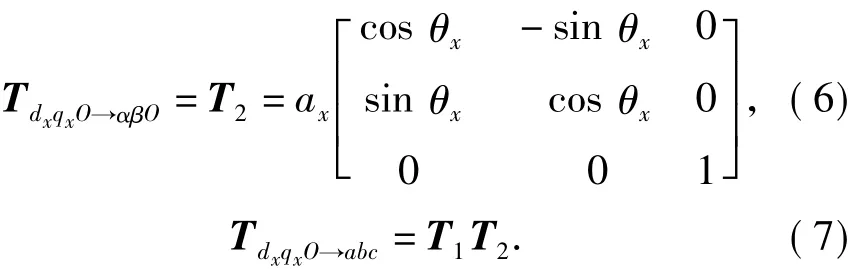
利用式(3)，(6)－(7)，将转矩计算式转换到dxqxO坐标轴中，对式(2)进行整理得

对Y形连接电机有

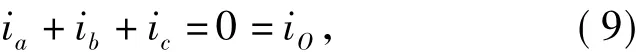
所以式(8)又可以改写成

如果令

结合式(4)可以将式(10)简化成

对于一个固定的电机，磁极数Pn是一个固定的数，所以在dxqxO坐标系中，电机电磁转矩与iqx成正比．而idx的值对电磁转矩的值无影响，它只会对电机运行过程中产生的磁场起增强或者减弱的作用，可以取其为0，或者取其与iqx成比例，再或者取其为一个固定的正数或负数．

将式(7)代入式(1)，可以得到在dxqxO坐标系中无刷直流电动机的数学模型为

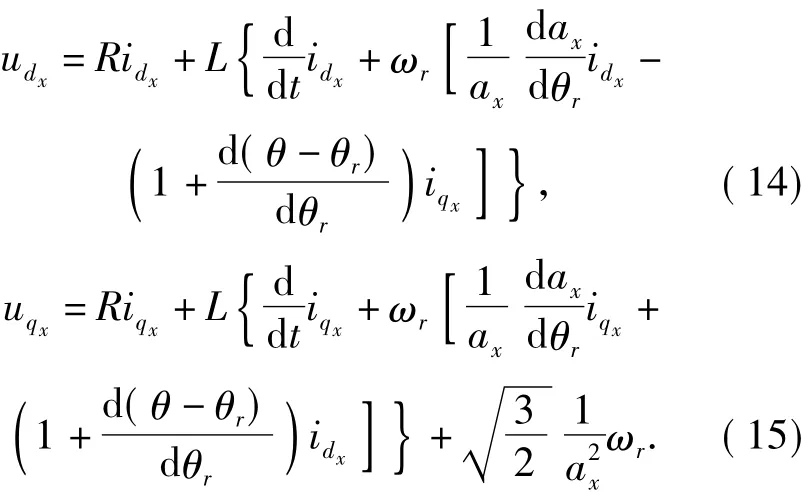
2 基于预测电流控制的转矩控制方法

2.1 BLDCM逆变器导通方式

无刷直流电机常见的导通方式有120°导通以及180°导通两种方式．120°导通是指电机在稳态运行时，只有两相导通，每隔60°换相一次，每一相在正负相各导通120°，所以其存在关断相，而关断相在换相时的电流脉动则是120°导通方式产生转矩脉动的主要原因．相应地，180°导通是指电机在稳态运行时，三相全部导通，每隔60°换相一次，每一相在正负相各导通180°，不存在关断相．

120°导通及180°导通产生的空间电压矢量在αβO坐标系中的位置如图2所示．

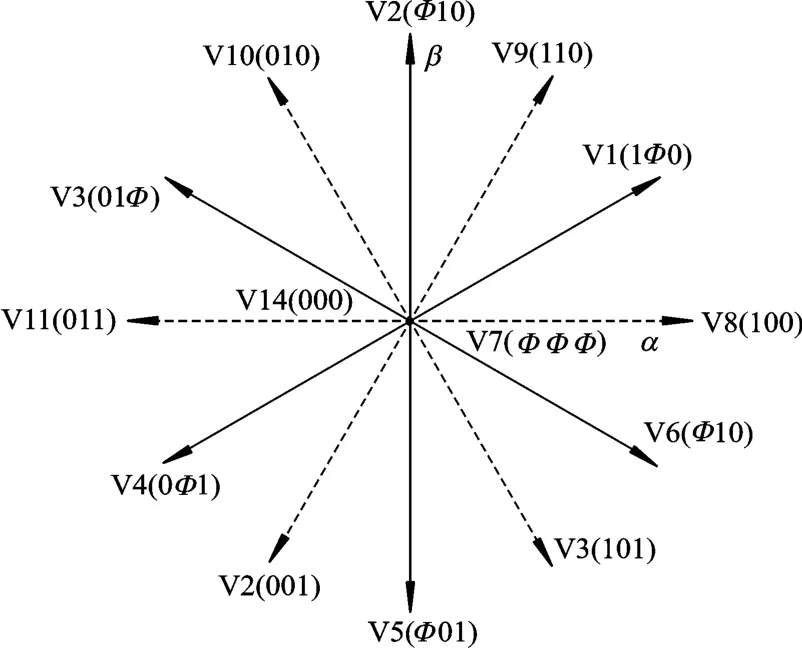
图2 两种导通方式下空间电压矢量

图2中实线为120°导通方式产生的空间电压矢量，虚线代表的是180°导通方式产生的空间电压矢量．当上桥臂开关管导通时以1表示，下桥臂开关管导通时以0表示，如果此相没有管子导通时以Φ表示．

2．2 120°导通模式电流预测控制原理

文献［8－9］提出的预测电流控制方案采用的导通方式是180°导通方式，而对于具有梯形反电动势的无刷直流电机，由于在120°导通方式下其每安培产生的转矩要大于180°导通方式，所以在大部分的应用场合中使用120°导通方式［2］，文中提出120°导通模式预测电流控制方案．其基本原理是:将式(14)－(15)进行近似离散化，然后选择120°导通模式下对应的电压矢量，计算出在下一个控制周期的电流值，并将此电流值与由速度控制环节及转矩控制环节产生的电流参考值作比较，通过适当的评价函数来选择要施加于电机上的电压矢量，从而实现对电流以及转矩的控制．

2．2．1 电流预测

首先，对式(14)－(15)作近似处理．

1)当控制周期Ts很小的时候，可以认为在下一个周期到来的时刻，电机的反电动势的值还未发生改变，于是根据ax以及θ的定义，可以近似地认为以及的值均为0．

2)同样在一个很小的控制周期Ts内，可以将电流的微分值近似为

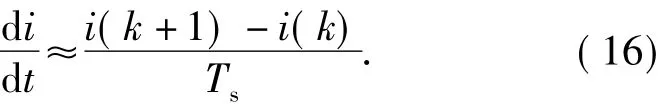
在经过上述近似处理之后，对式(14)，(15)进行离散化处理可得

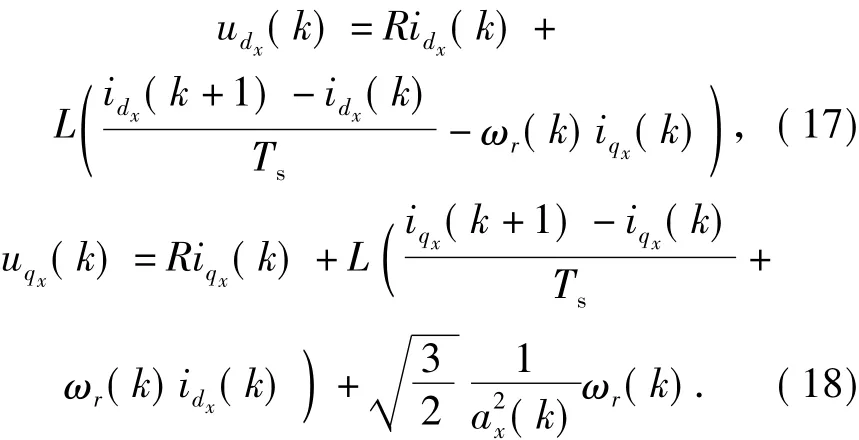
于是下一个控制周期的电流预测值可表示为

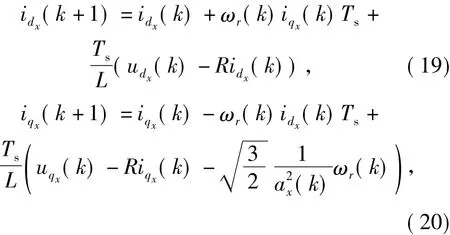
其中udx(k)，uqx(k)为当前控制周期所要施加的电压矢量的大小．在120°导通模式中，有7种可以使用的电压矢量，如图2中实线向量所示，其电压幅值为母线电压的从图2中可以看出，将30°(V)电压矢量投影到dxqxO坐标系中的关系式为

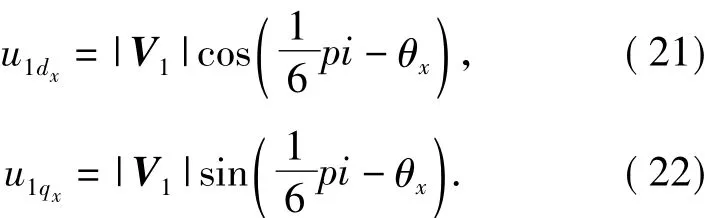
120°导通模式下7个空间电压矢量在dxqxO的投影关系见表1．

表1 120°导通模式下电压矢量在dx qx O坐标系中的投影

2．2．2 评价准则

评价准则函数是预测电流控制中选择空间电压的依据．通过上面的分析可知，控制iqx就可以控制电机的电磁转矩，于是可以选取下一个控制周期的iqx(k+1)与参考电流值iqx*之间的差值作为评价准则．但是仅仅对iqx做限制，而不对idx做任何限制，虽然可以实现对转矩的控制，但会造成电机的三相电流有较大的脉动，所以评价准则函数中还需包含idx(k+1)与参考电流值idx*之间的差值．于是构造的评价准则函数具体形式如下:

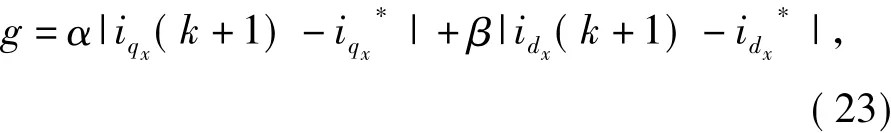
式中:α，β为权重系数;iqx(k+1)以及idx(k+1)的值是根据上一节中的(19)和(20)计算而得．iqx*以及idx*为下个控制周期的电流参考值．将速度控制器的输出作为转矩给定，与观测得到转矩Te比较，得到，由式(13)得到:

由于idx的值对电磁转矩的值无影响，可根据实际情况选取．为分析方便，取

电压矢量选择是根据评价函数值的大小来实现，其原则是选取使评价函数(23)值最小的电压矢量．将表1中对应的7个不同的电压矢量代入式(19)，(20)中可以得到在7组不同的电流预测值，再将这7组不同的电流预测值代入式(23)中，即可得到7个不同的评价准则函数值，其中最小的对应的电压矢量，即是当前时刻要施加的电压矢量．

2．3 混合导通模式控制原理

上一节提出了120°导通模式下的预测电流控制方案，可以在三相绕组中产生方波电流，但是由于绕组电感的存在，电流的上升时间和下降时间不可能无限短，使得实际的绕组电流并不是理想的方波，而且换相时同样也存在关断相电流的脉动，因此而引起转矩的脉动．文献［2］提出混合导通模式，在换相的过程中采用180°导通方式，来避免由于换相带来的转矩脉动，本小节借鉴此思想，提出基于混合导通模式的预测电流控制方案．

在上面120°导通的控制方式中，电压的选择是通过选取使评价函数值最小的电压矢量来实现的，所以要实现混合导通的控制方式，只需要在原来7个空间电压矢量的基础上再添加180°导通方式产生的电压矢量即可．在180°导通模式中，同样也存在7种可以使用的电压矢量，如图2中虚线向量所示，其电压幅值为母线电压的于是，在混合导通模式中，共有14个可以使用的电压矢量，将这14个电压矢量代入到评价函数中，得到14个评价函数值，通过选取最小值所对应的电压矢量即可实现混合导通模式的预测电流控制．180°导通模式下7个空间电压矢量在dxqxO的投影关系见表2．

表2 180°导通模式下电压矢量在dx qx O坐标系中的投影

续表

2．4 反电动势及转矩观测

反电动势值的观测可以参考文献［10］的方法，通过实际对电机的反电动势值与转速和转子位置之间的关系，离线构造出反电动势函数，再由位置传感器来实时确定反电动势的值．或者采用文献［7］的方法，构造出理想的梯形波反电动势函数，基本原理为具有梯形反电动势的无刷直流电机，其反电动势的幅值与转速成正比［7］，如果再假设反电动势的平顶宽度为x，则反电动势函数可以定义为三个相差120°，幅值为1的梯形函数．以A相反电动势函数为例，具体形式如下:

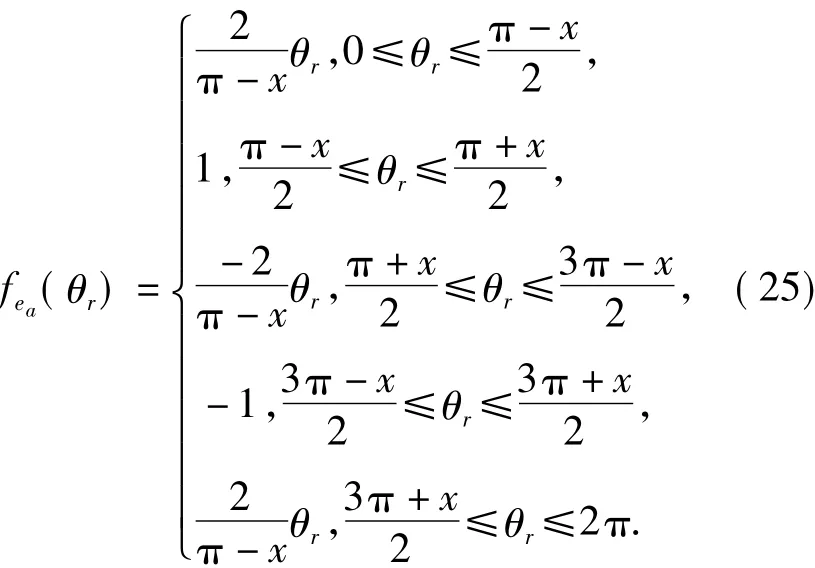
于是A相反电动势的值可以表示为

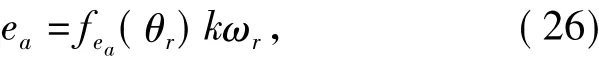
式中k为反电动势系数．然后再根据实际运行中的编码器输出的转子位置值，计算出转子速度值，代入式(26)，便可以求出实际的反电动势值．同理也可以得到其他两相的反电动势值eb，ec．

在文献［5］中，转矩的观测是通过求转子磁链的微分来实现的，这种方法不但需要大量的计算，而且由于微分的计算可能给转矩的观测带来较大的误差．故本文转矩的观测采取式(3)，需实时检测三相电流值和反电动势值．

2．5 控制系统设计

文中提出的BLDCM转矩控制系统结构框图如图3所示．

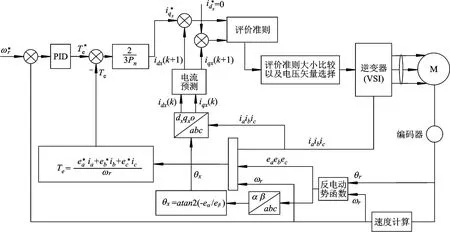
图3 控制系统结构框图

首先根据编码器输出的实际位置，计算出在abc坐标系中电机三相实时反电动势值，并转化成在αβO坐标系中的反电动势值，计算出θx．由θx的值以及三相电流的检测值实时计算出idx(k)以及iqx(k)，然后根据式(19)及(20)得出施加不同电压矢量时电流的预测值．最后根据评价函数(23)来选择适当的空间电压施加于电机，从而实现电机的电流以及转矩控制．

3 实例仿真

为验证文中算法，在Matlab/Simulink 2008b环境中搭建了基于电流预测控制的无刷直流电机转矩控制系统模型，控制系统结构框图见图3．控制系统选用的电机参数如下:R=2．875Ω;L=0．008 5 H;Te=1．4 N·m·A－1;P=4;额定电压300 V;额定转速 3 000 r·min－1;转动惯量 0．000 8 kg·m2．

速度环节控制器采用PID控制算法，其参数分别为比例系数kp=50，积分系数ki=0．001，微分系数kd=0．05．评价函数的权重系数取 α =1，β =0．01．

首先进行120°导通模式预测电流控制仿真，仿真过程为:t=0 s时速度指令为1 000 r·min－1，并一直维持至仿真结束;t=0．1 s时施加2 N·m的外部负载，并一直维持至仿真结束．仿真结果如图4所示．

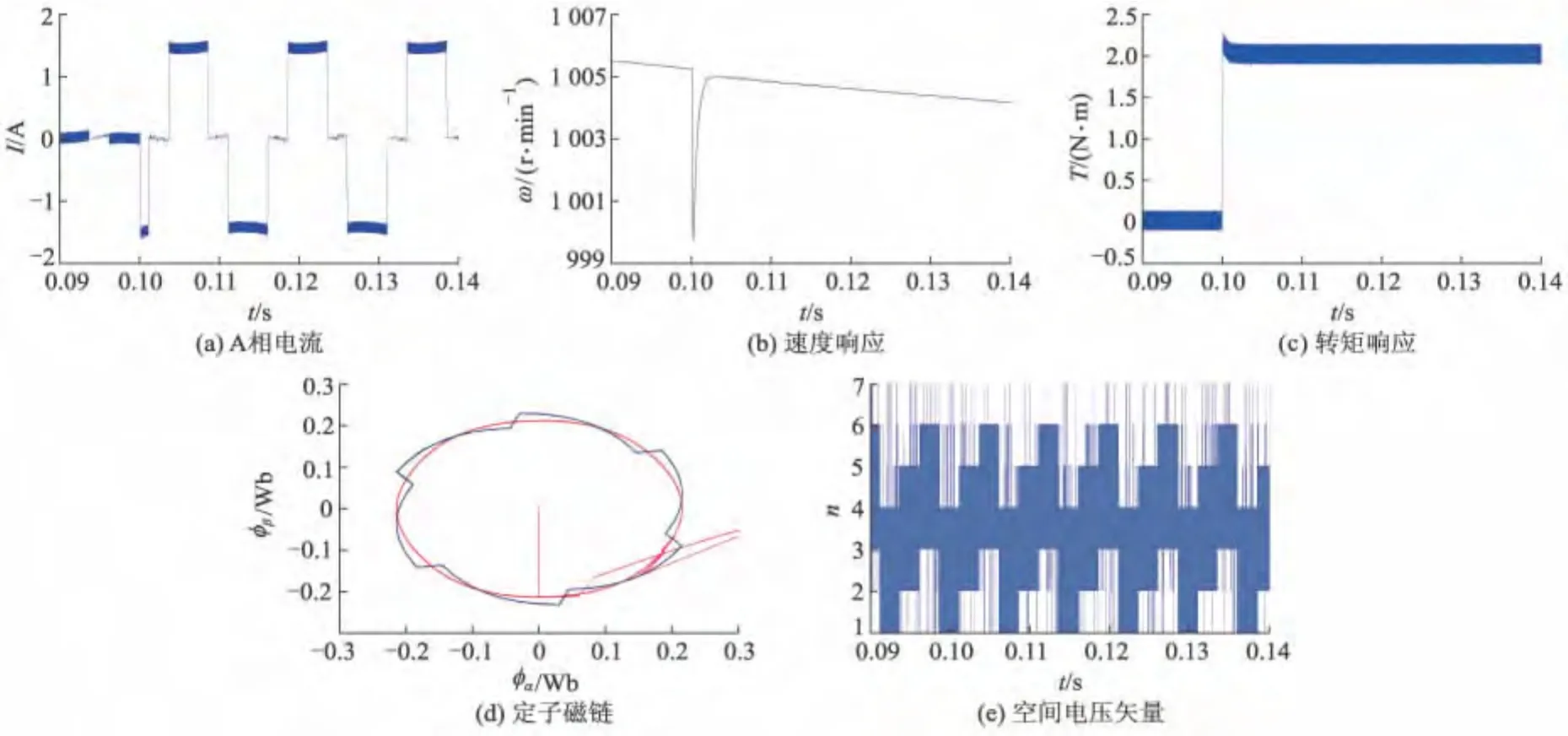
图4 1 000 r·min－1时采用120°导通模式响应曲线

由图4a可见，在t=0．1 s之前的空载电流较小，幅值为0．1 A左右，在t=0．1 s的时刻突加2 N·m的外加负载，使得电流发生突变，而在t=0．1 s之后，为平衡负载A相电流呈较标准的矩形，幅值为1．5 A，而且在换相的时刻虽然有较小的电流脉动，但是值不大．由图4b可见，在t=0．1 s的时刻，速度值从 1 005 r·min－1突变到 999 r·min－1，但是在 3 ms之后又回复到1 005 r·min－1．由图4c可见，在t=0．1 s时刻施加的2 N·m的外加负载的响应较好，而且t=0．1 s之后非换相时转矩保持在1．9～2．1 N·m，转矩脉动较小，而在换相时刻转矩脉动值稍大，转矩响应的最小为1．85 N·m．由图4d可见，其中红色圆形的曲线为t=0．1 s之前，即在外加负载施加之前的定子磁链，而蓝色类似于“花瓣形”的曲线为突加负载之后的定子磁链曲线．图4e为在电机运行过程中空间电压矢量的选用情况，其中n为电压矢量下标，即纵坐标的1对应表1中的V1，2对应表1中的V2，并以此类推．

然后进行混合导通模式下的预测电流控制仿真，仿真过程与上一致，仿真结果如图5所示．

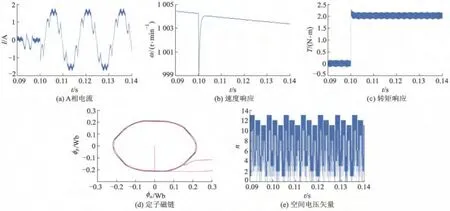
图5 1 000 r·min－1时采用混合导通模式响应曲线

由图5a可见，与120°导通方式一样在t=0．1 s之前的空载电流较小，但是混合导通模式下其幅值达到 0．5 A，且脉动较大，而在 t=0．1 s之后，为平衡负载A相电流呈正弦状，幅值为1．5 A，转矩脉动大．图5b为速度响应曲线．由图5c可见，在t=0．1 s时施加的2 N·m的外加负载的响应同样较好，而且 t=0．1 s之后转矩保持在1．85～2．15 N·m，转矩脉动较小，且不存在换相转矩脉动．由图5d可见，其中红色内环的曲线为t=0．1 s之前，即在外加负载施加之前的定子磁链，而蓝色外环的曲线为突加负载之后的定子磁链，明显混合导通模式下磁链曲线更接近圆形．由图5e可见，混合导通模式中，180°导通方式产生的空间电压矢量占主要部分．

最后，对文中所提出的两种控制方案在高速时转矩响应进行对比仿真．仿真过程为:t=0 s时速度指令为3 000 r·min－1，并一直维持至仿真结束;t=0．1 s时施加2 N·m的外部负载，并一直维持至仿真结束．仿真结果如图6所示．

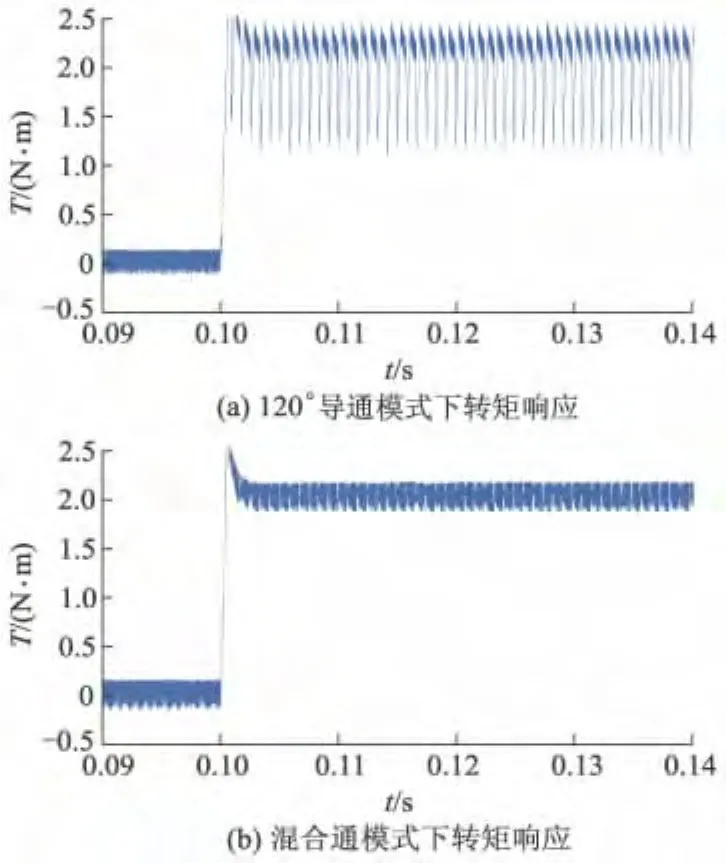
图6 3 000 r·min－1时两种控制方法转矩响应

由图6a 可见，在 3 000 r·min－1的速度时，120°导通模式下非换相时刻转矩能保持在2～2．4 N·m，而在换相的时刻转矩的最小值为1．082 N·m，可见120°导通模式下，高速时换相转矩脉动较大．由图6b可见，其转矩值保持在1．85～2．152 N·m，不存在换相转矩脉动．

综上，文中提出的120°导通模式预测电流控制方法以及混合导通模式预测电流控制方法，均能对转矩起到较好的控制效果．其中混合导通模式预测电流控制方法的电流脉动较大，而120°导通模式预测电流控制方法在高速时转矩脉动较大．

4 结论

1)在dxqxO坐标系下，无刷直流电机的转矩与qx轴的电流成正比．与永磁同步电机一样，通过控制交轴电流来实现转矩控制．

2)舍去了通常BLDCM控制系统中根据位置传感器来选择电压矢量的环节，通过评价函数值大小来实现电压矢量的选择，更方便于混合导通模式的实现．

3)两种基于不同导通模式的预测电流控制方法均能对转矩起到较好的控制效果，其中混合导通模式下的电流脉动较大而120°导通模式下在高速运行时换相转矩脉动较大．

References)

［1］Bharatkar S S，Yanamshetti R，Chatterjee D，et al．Comparison of switching schemes for brushless DCmotor drives［C］∥Proceedings of the 2010 ECTI International Conference on Electrical Engineering/Electronics，Computer，Telecommunications and Information Technology．Chiang Mai，Thailand:IEEE Computer Society，2010:1036－1040．

［2］Liu Y，Zhu Z Q，Howe D．Commutation-torque-ripple minimization in direct-torque-controlled PM brushless DC drives［J］．IEEE Transactions on Industry Applications，2007，43(4):1012 －1021．

［3］Lai Y S，Lin Y K．An unified approach to zero-crossing point detection of back EMF for brushless DC motor driveswithout current and hall sensors［J］．IEEE Transactions on Power Electronics，2011，26(6):1704 －1706．

［4］Liu Y，Zhu Z Q，Howe D．Direct torque control of brushless DC drives with reduced torque ripple［J］．IEEE Transactions on Industry Applications，2005，41(2):599－608．

［5］Gao Jin，Hu Yuwen．Direct self-control for BLDCmotor drives based on three-dimensional coordinate system［J］．IEEE Transactionson Industrial Electronics，2010，57(8):2836－2844．

［6］杨建飞，胡育文．无刷直流电机无磁链观测直接转矩控制［J］．中国电机工程学报，2011，31(12):90－95．Yang Jianfei，Hu Yuwen．Direct torque control of brushless DCmotorwithout flux linkage observation［J］．Proceedings of the CSEE，2011，31(12):90－95．(in Chinese)

［7］安群涛，孙立志，刘 超，等．无刷直流电机的磁链自控直接转矩控制［J］．中国电机工程学报，2010，30(12):86－92．An Quntao，Sun Lizhi，Liu Chao，et al．Flux linkage self-control based direct torque control of brushless DC motor［J］．Proceedings of the CSEE，2010，30(12):86－92．(in Chinese)

［8］Cortés P，KazmierkowskiM P，Kennel RM，etal．Predictive control in power electronics and drives［J］．IEEE Transactions on Industrial Electronics，2008，55(12):4312－4324．

［9］Morel Florent，Lin-Shi Xuefang，Rétif Jean-Marie，et al．A predictive current control applied to a permanent magnet synchronousmachine，comparison with a classical direct torque control［J］．Electric Power Systems Research，2008，78(8):1437 －1447．

［10］魏海峰，李萍萍，刘国海，等．基于双电流调节器的无刷直流电机换相转矩脉动抑制［J］．江苏大学学报:自然科学版，2010，31(6):691－694．Wei Haifeng，Li Pingping，Liu Guohai，et al．Commutation torque ripple reduction in burshless DC motor based on double current regulators［J］．Journal of Jiangsu University:Natural Science Edition，2010，31(6):691－ 694．(in Chinese)