M ixed noise removal for color images using quaternion representation

Wang DingchengTian YuhangChen BeijingShu Huazhong

（1Jiangsu Engineering Center of Network Monitoring，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（2School of Computer and Software，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（3Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（4Laboratory of Image Science and Technology，Southeast University，Nanjing 210096，China）

M ixed noise removal for color images using quaternion representation

Wang Dingcheng1，2，3Tian Yuhang2Chen Beijing1，2，3Shu Huazhong4

（1Jiangsu Engineering Center of Network Monitoring，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（2School of Computer and Software，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（3Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology，Nanjing University of Information Science and Technology，Nanjing 210044，China）

（4Laboratory of Image Science and Technology，Southeast University，Nanjing 210096，China）

In order to effectively restore color noisy images w ith themixture of Gaussian noise and impulse noise，a new algorithm is proposed using the quaternion-based holistic processing idea for color images．First，a color image is represented by a pure quaternionmatrix．Secondly，according to the different characteristics of the Gaussian noise and the impulse noise，an algorithm based on quaternion directional vector order statistics is used to detect the impulse noise．Finally，the quaternion optimal weights non-localmeans filter（QOWNLMF）for Gaussian noise removal is improved for the mixed noise removal．The detected impulse noise pixels are not considered in the calculation of weights．Experimental results on five standard images demonstrate that the proposed algorithm performs better than the commonly used robust outlyingness ratio-nonlocalmeans（ROR-NLM）algorithm and the optimalweightsmixed filter（OWMF）．

color image denoising；Gaussian noise；impulse noise；mixed noise；quaternion

D igital images are easily degraded by noise during acquisition，digitization and transm ission．The influence factors include the quality of the sensor components and environmental conditions in image acquisition，the transm ission channel interference in image transm ission，and so on．However，in many cases，the digital image w ill be degraded by these factors at the same time．Consequently，the image w ill be corrupted by m ixed noise［1］．

In order to restore the color noise image w ith them ixture of Gaussian noise and impulse noise，many studies have been published during the last few decades．Among them，Xiong et al．［2］proposed the robust outlyingness ratio-nonlocal means（ROR-NLM）algorithm．They utilized the robust outlyingness ratio algorithm to detect the impulse noise pixels，and then applied the non-local means filter tw ice to remove impulse noise and Gaussian noise，respectively．Lin et al．［3］presented the sorted quadrantmedian vector sw itching bilateral filter（SQMVSBF）．This filter first took the median values of four small w indows divided from the neighborhood w indow of current pixel to form a new vector，then detected the impulse noise from this vector after sorting，and finally removed them ixed noise by sw itching different types of bilateral filters，based on the detection results．Jin et al．［4］proposed the optimal weights m ixed filter（OWMF）based on the improved rand-ordered absolute differences algorithm and the optimal weighting filter for Gaussian noise．However，these works mainly focus on grayscale images．Although one can use these works to separately process each channel of color image，this approach fails to consider the entirety of the three channels and the inherent correlation among the three channels．

Since the1990s，the algebra of quaternions has been extensively considered for color image processing by using the quaternion representation of color images．This representation encodes three channels of each pixel into three imaginary parts of a quaternion number．It can process a color image holistically as a vector field and handles the coupling between the color channels naturally［58］．Based on this representation，many classical algorithms and tools for grayscale images have been effectively extended to color image processing，such as the Fourier transform，wavelet transform，neural networks，principal component analysis，the support vectormachine，and so on．

For the color image noise removal，there are also some quaternion-based studies：for the impulse noise，such as the quaternion weighted vectormedian filter［9］，the sw itching vectormedian filter based on quaternion rotation［10］，the algorithm based on quaternion representation and a di-rectional vector order-statistics［5］；for the Gaussian noise，such as the quaternion optimal weights non-local means filter（QOWNLMF）［6］；for the Poisson noise，such as quaternion weighted mean filter［7］．However，the quaternion-based work for m ixed noise removal has not yet been reported in the literature so far．In this paper，a new quaternion-based algorithm for color image mixed noise removal is proposed by combining the impulse noise detection algorithm shown in Ref．［5］w ith an improved algorithm of QOWNLMF［6］．

1 Some Prelim inaries

1.1 Quaternions and quaternion rep resentation of color images

Quaternionswere introduced in 1843 by themathematician Hamilton．The basic form of a quaternion is given by

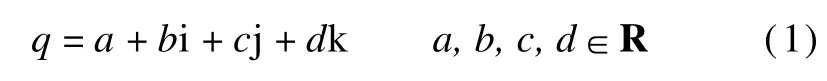
where i，j，k are three imaginary units，which satisfy the following rules：

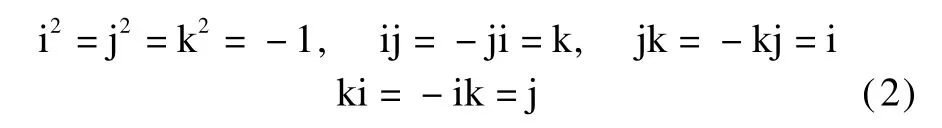
When a＝0，q is called a pure quaternion．Themodulus and conjugate of the quaternion q are，respectively，defined as

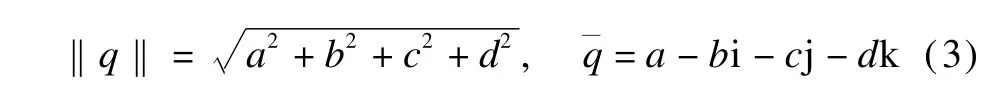
Using the quaternion representation of color images，a color image f（x）can be represented as

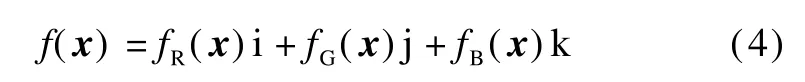
where fR（x），fG（x），fB（x）represent the red，green，and blue channels of the pixel x，respectively．

1.2 Color image im pulsive noise removal based on quaternion representation and directional vector order-statistics［5］

The commonly used impulse noise model can be described as

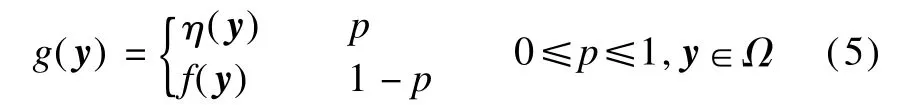
where f（y），g（y）andη（y）are the original pixel value，the observed noisy one and the impulse noise at a pixel y，respectively；p is the density of impulse noise；Ωis the image definition domain．

Jin et al．［5］proposed an algorithm based on quaternion representation and a directional vector order statistics algorithm．The detailed steps of their algorithm are as follows．

1）Select the pixels lying in the four directions（0°，45°，90°，and 135°）of the 5×5 neighborhood centered at the current pixel q and denote them as hi（i＝1，2，3，4）．

2）Count the number of sim ilar pixels in the four in directions hi，denoted as card（hi），and mark the direction w ith the greatest number of sim ilar pixels as h*．

3）Determ ine the impulse noise pixel and remove it using the follow ing equation：

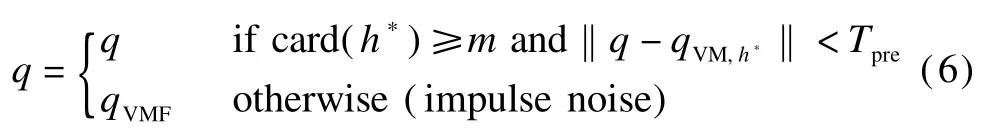
where m and Tpreare the predefined thresholds；‖·‖is the modulus of quaternion defined in Eq．（3）；qVMFrepresents the vectormedian of the 5×5 neighborhood of the pixel q．

1.3 Color image Gaussian noise removal based on quaternion representation and QOWNLMF［6］

The commonly used Gaussian noise corruption ismodeled as

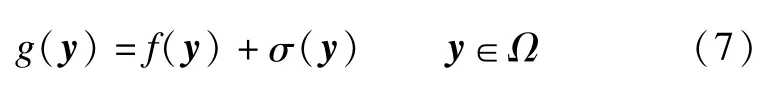
whereσ（y）is the noise perturbation at pixel y．Moreover，σ（y）are independent and identically distributed Gaussian random variableswith zeromean andσstandard deviation．

The basic idea of optimal weights non-localmeans filter is to estimate the unknown original image f（x）by a weighted average of noise image g（y）．

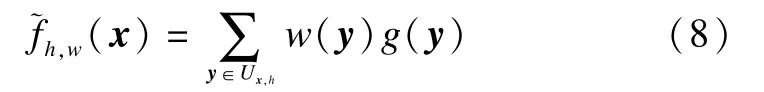
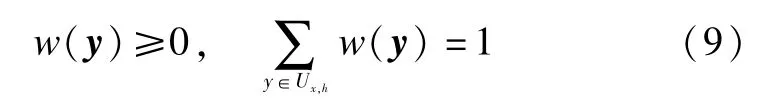
Chen et al．［6］first used the quaternionmean square error（QMSE）to quantify the difference between the restored quaternion value~fh，w（x）and the unknown original one f（x）．After that，using themethod of Lagrangemultipliers，they obtained the optimal weights m inim izing a tight upper bound of the QMSE under the constraints（9）．The weights are given by

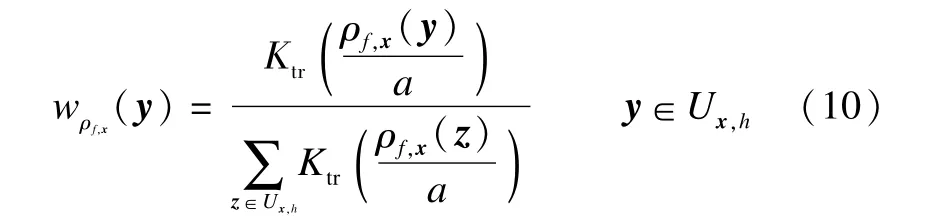
Here，some related variables are defined as follows：

1）ρf，x（y）is calculated by

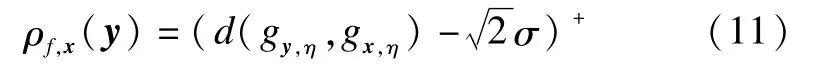
where（·）＋represents the positive part of a real number as

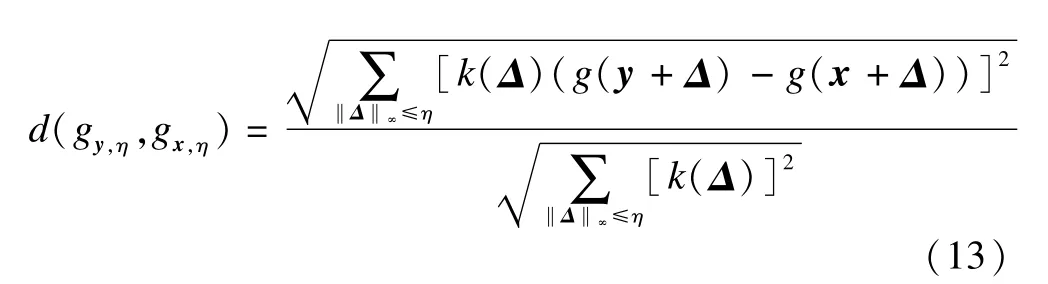
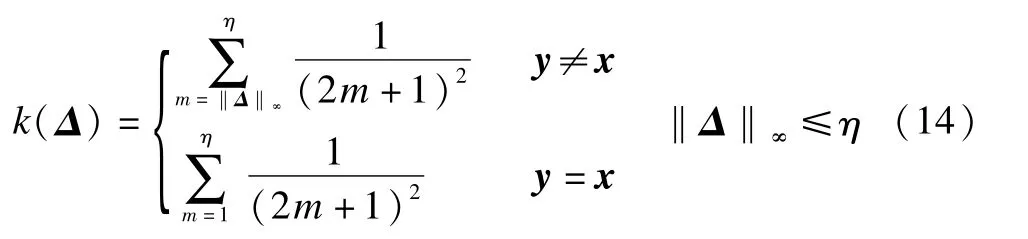
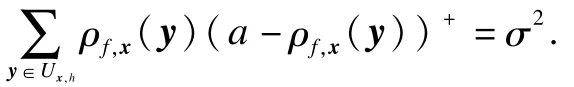
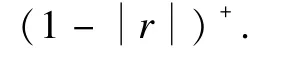
Substituting the weights given in Eq．（10）into Eq．（8），Chen et al．［6］proposed the QOWNLMF to remove Gaussian noise in color images．

2 Proposed Algorithm

The commonly used m ixed noise w ith the m ixture of Gaussian noise and impulse noise can bemodeled as

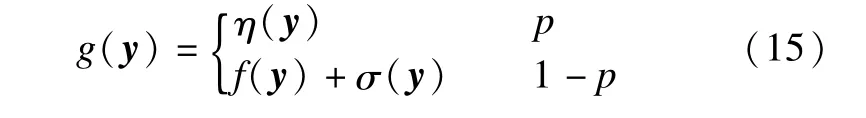
where 0≤p≤1，y∈Ω．

Since the quaternion-based approaches aremore appreciated than the component-w ise methods in color image processing，the proposed algorithm combines the two quaternion-based algorithms described in Section 1．The impulse noise pixels are detected before the m ixed noise removal．The flowchart of the proposed algorithm is given in Fig．1．

Fig.1 Flowchart of the proposed mixed noise removal algorithm

Let g（y）be the noise image．The main steps of the proposed algorithm are as follows：

1）Quaternion representation of color images．Since the quaternion representation of a color image given in Eq．（4）can process the color image holistically and consider the relationship among three channels，it is used to represent g（y）．

2）Impulse noise detection．By traversing the image g（y），the algorithm described in Section 1．2 is used to detect impulse noise pixels．

3）M ixed noise denoising．By traversing the image g（y）again，the filter QOWNLMF presented in Section 1．3 for Gaussian noise removal is improved for mixed noise removal．

The improvedmeasures and their reasons are as follows：

1）Since the impulse noise pixels do not contain the useful information for restoring the image，only the impulse-free pixels in a current w indow were considered in the QOWNLMF proposed by Chen et al．［6］to remove m ixed noise．Therefore，the improved QOWNLMF for m ixed noise removal is as follows：

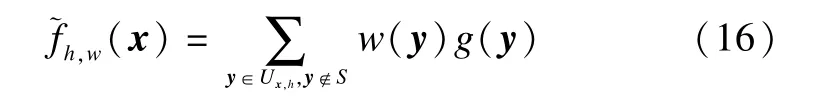
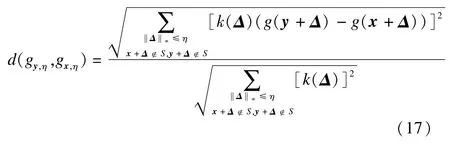
where S is the detected noisy pixel set；w（y）are the weights given in Eq．（10）updated by

2）W ith the increase in the density of impulse noise，fewer and fewer pixels are available in a sim ilarity w indow and a search w indow w ith the fixed size since only non-impulsive noise pixels are considered．This leads to the low quality of restored image．Therefore，we propose to adaptively adjust the size of the search w indow according to the density of impulse noise instead of the size of the similarity window．The reasons are as follows：on the one hand，it is difficult to adjust both w indows at the same time；on the other hand，Chen et al．［6］pointed out that“the pixel values in the sim ilarity w indow are only used to obtain the weights of the pixel values in the search w indow．Therefore，the search w indow plays amore important role than the similarity w indow．”

3 Experimental Results

In order to evaluate the performance of the proposed algorithm，five color standard images w ith size 256×256 shown in Fig．2 are considered．They are added to the m ixed noises w ith different degrees：the standard deviation of Gaussian noise varies w ith 12，14，16，18 and 20；the density of impulse noise varies w ith 2%，4%，6%，8%and 10%．Then，these noisy test images are restored by the proposed algorithm．

During the implementation of the proposed algorithm，two thresholds in the impulse noise detection stage are set as Tol＝48 and m＝3；the sim ilarity w indow size is 11× 11；the search w indow size is adaptivew ith the density of impulse noise under the consideration of the speed and the denoising efficiency．They are given in Tab．1．

Fig.2 Five color standard images w ith size 256×256．（a）Lena；（b）Peppers；（c）Girl；（d）M ilkdrop；（e）Parrots

Tab.1 Size of the sim ilarity w indow size and the search w indow size for different densities of impulse noise

We compare the proposed algorithm w ith two recentalgorithmsmentioned in the introduction section，the RORNLM algorithm［2］and the OWMF algorithm［4］．The commonly-used PSNR（peak signal-to-noise）is used to measure the quality of the restored image．Tab．2 shows the PSNR values of three algorithms for five test images affected by various degrees ofm ixed noise．In addition，Fig．3 provides the difference of the average PSNR values between the proposed algorithm and the compared algorithms．The average PSNR values correspond to five test images．It can be observed from Tab．2 and Fig．3 that the proposed algorithm is superior to both of the two compared algorithms．All of the difference values between the proposed algorithm and the ROR-NLM are greater than 1 and those between the proposed algorithm and the OWMF are greater than 0．5．Themain reason is that the proposed algorithm is a quaternion-based algorithm，which processes a color image holistically and considers the inherent correlation among the three channels of a color image．

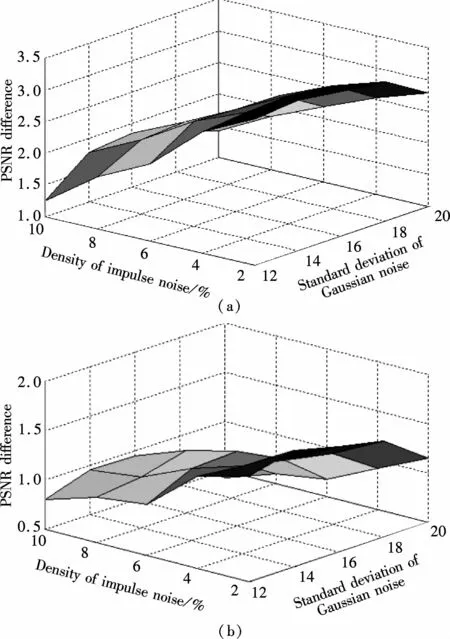
Fig.3 Differences of the PSNR values between the proposed algorithm and compared algorithm for different noise degrees．（a）Proposed algorithm and ROR-NLM；（b）Proposed algorithm and OWMF

In order to visually illustrate performance，the restored images for noisy images shown in Fig．4 and their corresponding error images of three compared algorithms are given in Fig．5 and Fig．6．In Fig．4，σis the standard deviation of Gaussian noise，p is the density of impulse noise．These results show that，for both Fig．4（a）w ith the relative low level noise and Fig．4（b）w ith the heavy one，the performance of the proposed algorithm is better than that of the other two compared algorithms．The proposed algorithm can retain more texture details than the other two compared algorithms，especially for themarked area in Fig．5 and Fig．6．

Fig.4 Two noisy images corrupted by am ixed noise w ith different noise levels．（a）σ＝12，p＝2%，PSNR＝20．825 1；（b）σ＝20，p＝10%，PSNR＝14．425 2

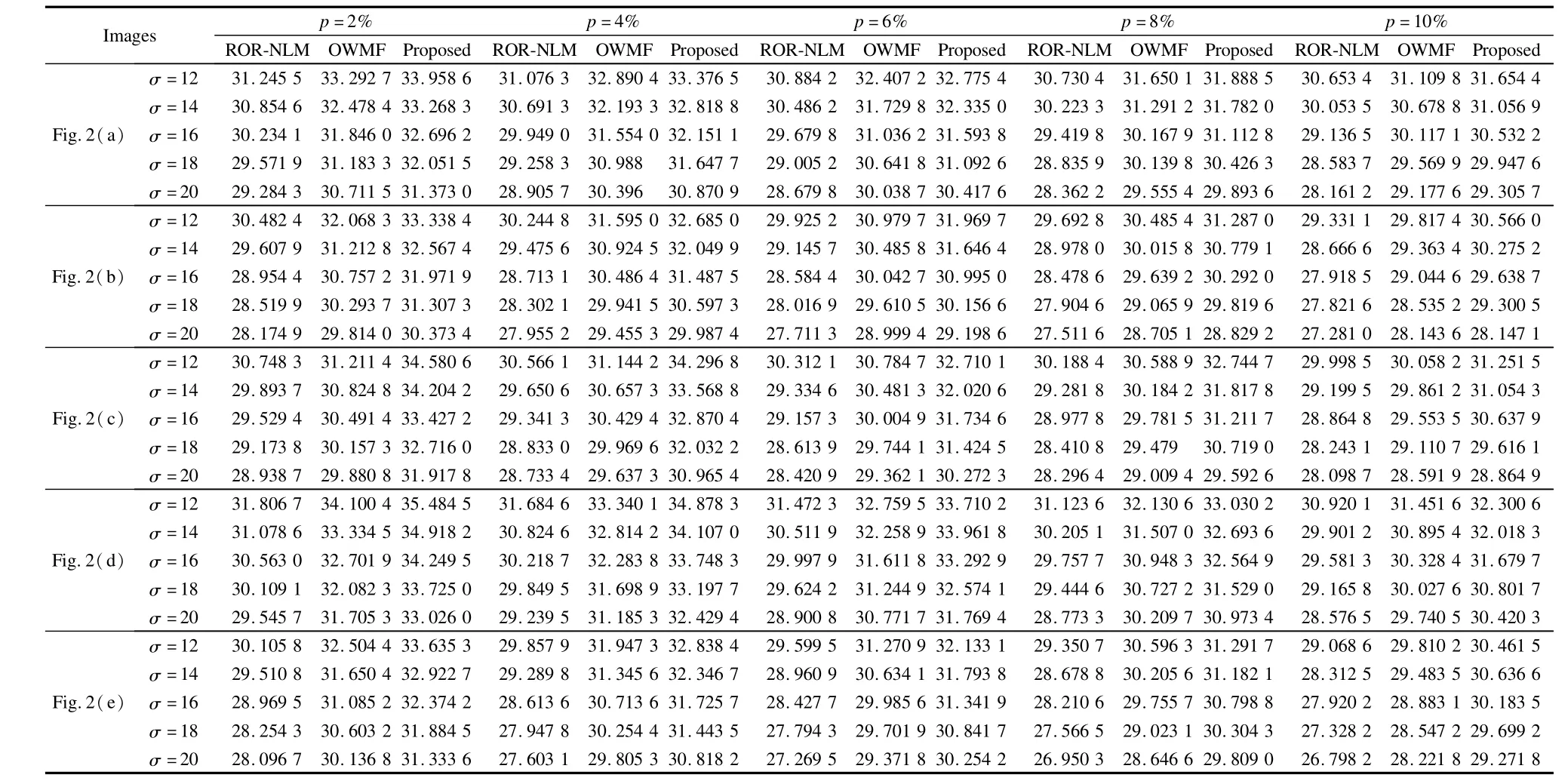
Tab.2 PSNR values of three algorithms for five color imagesw ith varying degrees ofm ixed noise

Fig.5 Restored images of Fig．4（a）and five timesmagnified error images using different algorithms．（a）ROR-NLM（PSNR＝31．245 5）；（b）OWMF（PSNR＝33．292 7）；（c）Proposed algorithm（PSNR＝33．958 6）

Fig.6 Restored images of Fig．4（b）and five timesmagnified error images using different algorithms．（a）ROR-NLM（PSNR＝26．798 2）；（b）OWMF（PSNR＝28．221 8）；（c）Proposed algorithm（PSNR＝29．271 8）

4 Conclusion

In this paper，a new denoising algorithm，which removes the m ixture of Gaussian noise and impulse noise for color images，is proposed．The proposed algorithm based on quaternion representation deals w ith a color image in a holistic manner and considers the correlation between the color channels sufficiently．Form ixed noise removal，the proposed algorithm improves the QOWNLMF and then combines the improved QOWNLMFw ith the existing quaternion-based impulse noise detection algorithm．Experimental results show that the proposed algorithm performs better than the commonly used ROR-NLM algorithm and OWMF filter．

［1］Jin L H．Color image filtering and quaternion-based color image processingmethods［D］．Wuhan：Institute for Pattern Recognition and Artifical Intelligence，Huazhong University of Science and Technology，2008．（in Chinese）

［2］Xiong B，Yin Z P．A universal denoising framework w ith a new impulse detector and nonlocal means［J］．IEEE Transactions on Image Processing，2012，21（4）：1663-1675．

［3］Lin C H，Tsai JS，Chiu C T．Sw itching bilateral filterw ith a texture／noise detector for universal noise removal［J］．IEEE Transactions on Image Processing，2010，19（9）：2307- 2320．

［4］Jin Q Y，Grama I，Liu Q S．Optimal weightsm ixed filter for removing m ixture of Gaussian and impulse noises［J／OL］．arXiv preprint，2012．http：／／arxiv．org／pdf／1205．3999v1．pdf．

［5］Jin L H，Liu H，Xu X Y，et al．Color impulsive noise removal based on quaternion representation and directional vector order-statistics［J］．Signal Processing，2011，91（5）：1249- 1261．

［6］Chen B J，Liu Q S，Sun X M，etal．Removing Gaussian noise for colour images by quaternion representation and optim isation of weights in non-localmeans filter［J］．IET Image Processing，2014，8（10）：591- 600．

［7］Chen B J，Dai H，Liu Q S，etal．Poisson noise removal for color images using quaternion representation［J］．Journal of Southeast University：Natural Science Edition，2013，43（4）：717- 723．（in Chinese）

［8］Chen B J，Shu H Z，Coatrieux G，et al．Color image analysis by quaternion-type moments［J］．Journal of Mathematical Imaging and Vision，2015，51（1）：124-144．

［9］Jin L H，Liu H，Xu X Y，et al．Quaternion-based color image filtering for impulsive noise suppression［J］．Journal of Electronic Imaging，2010，19（4）：043003-01-043003-12．

［10］Jin L H，Li D H．A sw itching vectormedian filter based on quaternion rotation［J］．Journal of Image and Graphics，2007，12（12）：2089- 2095．（in Chinese）

基于四元数表示的彩色图像混合噪声去噪

王定成1，2，3田宇航2陈北京1，2，3舒华忠4

（1南京信息工程大学江苏省网络监控工程中心，南京210044）
（2南京信息工程大学计算机与软件学院，南京210044）
（3南京信息工程大学江苏省大气环境与装备技术协同创新中心，南京210044）
（4东南大学影像科学与技术实验室，南京210096）

为了能够更加有效地恢复受混合高斯和脉冲噪声污染的彩色图像，采用基于四元数的彩色图像整体处理方案，提出了一种彩色图像混合噪声去噪算法．首先，通过一个纯四元数矩阵表征一幅彩色图像；然后，根据高斯噪声和脉冲噪声的不同特性，采用基于四元数方向矢量排序统计的算法检测脉冲噪声位置；最后，将针对高斯噪声的基于四元数最优权值的非局部均值滤波器进行改进以应用于混合噪声图像去噪，在权值计算时不考虑已被检测出的脉冲噪声点．对5幅标准图像的实验结果表明，所提算法的去噪效果优于目前常用的ROR-NLM（robust outlyingness ratio-nonlocalmeans）算法和最优权值混合滤波器．

彩色图像去噪；高斯噪声；脉冲噪声；混合噪声；四元数

TP391

10．3969／j．issn．1003－7985．2015．03．008

2014-12-11．

Biography：Wang Dingcheng（1967—），male，doctor，professor，dcwang2005＠126．com．

s：The National Natural Science Foundation of China（No．61572258，61173141，61271312，61232016，61272421），the Natural Science Foundation of Jiangsu Province（No．BK2012858，BK20151530），the Natural Science Foundation of the Jiangsu Higher Education Institutions of China（No．13KJB520015），Open Fund of Jiangsu Engineering Center of Network Monitoring（No．KJR1404）．

：Wang Dingcheng，Tian Yuhang，Chen Beijing，et al．M ixed noise removal for color images using quaternion representation［J］．Journal of Southeast University（English Edition），2015，31（3）：347- 352．

10．3969／j．issn．1003－7985．2015．03．008