基于IR-UWB系统的高速准循环LDPC编解码器设计＊

曾 辉 黄 鲁 杨灿美

（中国科技大学电子与科学技术系，合肥，230027）

引 言

通信系统将具有更高的数据传输速率，且逐渐转向宽带通信。其中超宽带系统最为典型。超宽带系统拥有更宽的带宽（3.1～10.6GHz）以及高的数据传输速率（802.15.3a协议下的数据速率大于100 Mb／s），并且系统复杂度很低，硬件消耗低。为了提高数据高速传输的可靠性，LDPC成为UWB系统中极为重要的信道编码方式，因为它有近乎香农极限（Shannon-Limit）的纠错能力。

LDPC由Gallager［1］在1962年提出，它的硬件实现较复杂。因为当时硬件的集成水平的限制，直到20世纪90年代，Mackay重新研究LDPC码，才引发对其的研究热潮。文献［2］给出了离Shannon极限只有0.004 5dB的LDPC码，但是随机构造法使得实现较为困难，硬件实现过于复杂。文献［3］提出了准循环矩阵的方式能更有效地实现LDPC码校验矩阵的构造。

本文的IR-UWB系统用来实现高速率视频的实时通信，系统基带是单比特接收机［4］以二次微分式高斯脉冲调制每比特信息的方式实现长物理帧的传输，为减少时延，决定采用并行编译码。UWB系统也采用其他编码方式，例如RS［5］，Turbo［6］以及组合码［7］等。RS码相对其他线性分组码，同码率时纠错能力较强，硬件复杂度低［8］，但只限于中短型码。而Vertebi，Turbo等卷积码，其较高的译码复杂度，卷积码更适于串行传输。相比之下，LDPC对长码字的性能更优异，每个物理帧传输的有效码作为一个编码单元。译码复杂度高于RS码，但低于Turbo，可实现完全并行译码［9］。

1 校验矩阵的构造与编码

LDPC码是一类基于稀疏校验矩阵（H阵）的线性分组码，可在硬件上有效实现的LDPC编码有Hu等提出的渐进边增长（Progressive edge-growth，PEG）算法。此法采用逐步优化的思路，通过在Tanner图（图1）上依次添加边来构造最终的结点关系图，每次添加的边都尽可能地减少对图中其他边的影响，具体算法见文献［10］。虽然纠错性能好，但无法简单编码，不太适于长码，并且译码存储复杂度过高。

图1 基于Tanner图的LDPC信息传递Fig.1 LDPC message channel based on tanner

根据香农理论，构造随机矩阵在硬件上难以实现，由此诞生了由几何代数的方法构造LDPC校验矩阵——准循环［3］，即用循环移位矩阵块构造H阵。常用的循环移位矩阵有I矩阵、D矩阵和Q矩阵。Q矩阵中“1”的分布无规律，可以通过皇后算法获得，但需用额外的存储空间，一般用查找表的方式在硬件上实现。

然而，直接以QC实现长码字校验矩阵的构造硬件实现仍显复杂，译码存储不易实现。文献［11］给出了校验矩阵PEG构造方法，PEG算法构造的Tanner图具有最小的距离和良好的环长（图1粗线示），这些环长对信息概率的统计不利，使得节点之间传递的外部消息的独立性降低，削弱了抗干扰能力。结合QC-LDPC码的循环矩阵构造LDPC校验矩阵，在中短码长时可以获得与随机构造的规则码相当的性能。文献［11］阐述的构建较大围长的LDPC校验矩阵方法——消环算法，消除H阵中的短环（一般消除4，6和8环）。

综上所述，可先用PEG算法构造基矩阵，在所记录的环中取出长度最短环的“1”元素，消除Tanner图中的短环，“0”元素用“-1”替代；接着，随机产生子矩阵偏移量代替矩阵中非“-1”元素，并用相应维的循环移位Q矩阵或I矩阵代替矩阵中的对应其偏移量的元素，可进一步消除所生成H阵中的短环，“-1”代表该循环矩阵为全零矩阵。这种H阵的构造法，大大降低了硬件实现的复杂度，更适于长型码字，译码存储也简单得多。

1.1 仿真结果与分析

IEEE 802.15.3a协议关于UWB信道给出了基于S-V模型的4种场景模式，具体UWB室内信道特征见文献［12］。其中存在视距信号的CM1模式，其主要考虑加性高斯白噪声（Additive white Gaussian noise，AWGN），多径干扰以及信号幅度呈现近乎对数正态分布的衰落。信道相对其他场景更稳定，适合近距离室内UWB通信系统模拟仿真。

本系统采用BPSK调制，编码器的设计旨在实现校验矩阵性能的比较，因此可选择二进制加性高斯白噪声信道，采用一般的MS译码方式。仿真中分别以原始PEG算法和本文阐述的算法（I与Q循环矩阵）构造3类不同的H阵：码长n＝900（PEG适于中短型码），码率R＝1／2，变量节点的维度分布［10］为λ（x）＝0.3x＋0.16x2＋0.17x3＋0.37x6，每个循环移位矩阵定为维长15的I／Q矩阵（Q阵中任选其一）。译码迭代次数为15。图2显示了其性能曲线，该设计阐述的构造校验矩阵的方式，性能更接近于PEG算法。Q矩阵作为准循环矩阵，性能更显优越。

图2 I／Q矩阵的QC-LDPC性能比较Fig.2 I／Qmatrix QC-LDPC performance comparison

图3显示PEG算法与本文讨论的算法在码率R＝1／2和5／6下的仿真实验结果（其他条件相同）。由图可见，信噪比较低时，基于I矩阵和Q矩阵QC-LDPC的性能相当；高信噪比时，基于Q矩阵的LDPC优于基于I矩阵的LDPC码的性能，而随着码率的升高，两者的性能都有所降低。对于R＝1／2码率，码长为n＝1 800，误码率为低于10-6时，两者SNR都在2dB左右。

1.2 快速并行编码实现

令x为待编码的信息序列，p为校验序列，根据校验矩阵H的定义

线性分组码的一般性特征：n为信息位长（矩阵块数），m为校验阵部分的块数，左边为信息比特部分，右边为校验比特部分。

图3 R＝1／2和5／6，I／Q矩阵 QC-LDPC性能对比Fig.3 R＝1／2or 5／6 I／Qmatrix QC-LDPC performance comparison

式（2）分解为以下形式

式中：表示矩阵的第m行元素，表示矩阵中第m行n列的元素。这种编码方式可实现并行高速编码。

综上分析，低发射功率的UWB（-41.3dBm／MHz）接收端信噪比较低，选择I矩阵更适合在电路中实现，其不需要I矩阵的存储空间，矩阵运算时只需循环矩阵的移位矢量就可实现有效编码。文献［13］采用可配置循环移位寄存器实现高速并行编码；译码存储也相对简单，否则，需要额外用上Q矩阵的存储空间和独立的矩阵运算单元。

2 改进型最小和译码

LDPC通常译码方式主要有软判决的置信译码（Belief propagation，BP）和加权比特翻转（Weighted bit flip，WBF）的迭代译码，如文献［14］复合译码性能的分析。本决定采用性能更优越，复杂度较高的BP译码来满足本系统高性能的要求，其通用的有对数域BP，以及在其基础上改进的最小和译码。为降低复杂度又提出了改进型最小和，主要对其中φ（x）近似。文献［15］提出了用线性函数逼近方法分段地处理以达到近似φ（x）函数的目的，但是其硬件实现的复杂度过高。实际运用中只需用个变量因子分段近似即可，分段区间是有限的，因子取值相对有限，并且这个变量也可用来均衡信道信噪。

2.1 变量因子最小和译码

φ（x）表达式如下

图4为φ（x）的示意图，随x的增大，φ（x）值呈下降指数迅速减小，所以｜L（rji）｜中占主要作用的是绝对值较小的βi′j＝｜L（qji）｜，从而简化对数BP译码算法，可得

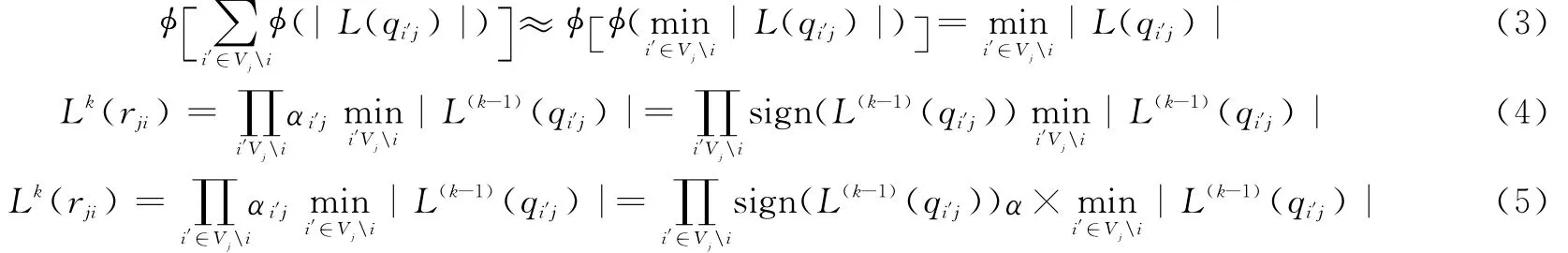
变量节点v利用校验节点传递的第k次迭代的信息Lk（rj′i）计算信息节点信息Lk（qij）

出于节省存储空间的考虑，解码算法如下

Min的取值是个近似的结果，添加调整参数α，让其更近似于对数域BP，如式（5）所示。对比两种算法流程，解码算法中Lk（rji）（校验节点传递给变量节点相关概率信息）更新不需要L（qi′j）（变量节点传递给校验节点的相关概率信息），只需要计算Lk-1（Qi）-L（k-1）（rji），这样减少了解码过程中信息的存储量。

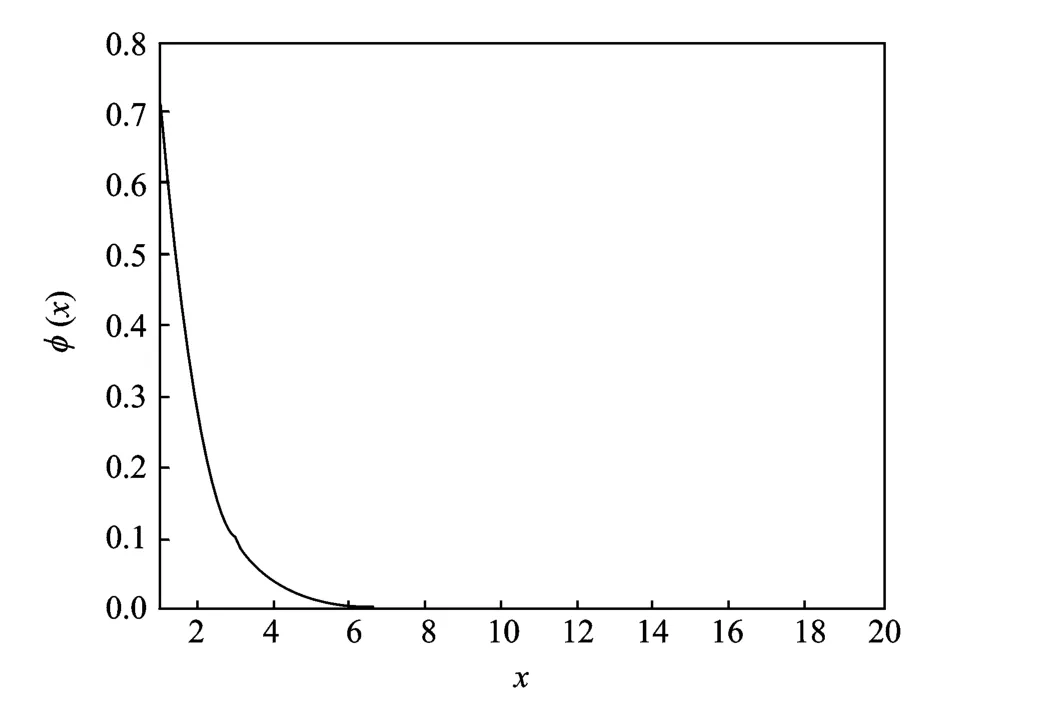
图4 函数φ（x）示意图Fig.4 Functionφ（x）sketch

2.2 译码仿真结果分析

鉴于UWB系统实时传送的物理帧长，以及校验矩阵的构造方式，选择（n，k）＝（1 800，900）的码字，循环移位维长定为30。该系统接收机［4］在信道估计时提取的每比特概率信息可直接用于LDPC译码。仿真在CM1场景模型［9］下进行，译码迭代次数为20，输入20帧数据，图5给出了对数BP与变量因子MS译码的性能结果。实验中对MS算法进行α取值遍历，从图中可以得到在低信噪比时，两种译码的性能差距较小，但随着信噪比的增大，对数译码BP仍显示其优良的性能。对较低信号发射功率的UWB系统，该改进的MS译码更适合于UWB系统，因为其硬件实现复杂度低于对数BP译码，且其译码具有调节功能。图中α＝0.85或0.95时，译码性能优于对数BP，在硬件实现中，只需要加乘法器即可，而α的取值可在量化分析后获得。

图5 （1 800，900）LDPC码在α下的性能遍历Fig.5 （1 800，900）LDPC performance traversal onα

图6显示了（1 800，900）码字在α＝0.8时不同迭代次数下的译码性能。可以看出，随着迭代次数的增加，BER呈下降趋势。信噪比较低时，性能没有因迭代次数而有较大的改变，拥有较低的译码延迟，这更有利于UWB系统高速率传输的特性。当迭代次数超过15时，BER＝10-6，信噪比小于3.3dB。迭代运算过程中如果c×HT＝0成立，则译码成功，反之，迭代次数达到指定数 （具体得实际测试而定）时退出，译码结束。

图6 （1 800，900）码字在迭代次数不同的性能Fig.6 （1 800，900）performance comparison on traversal num

3 结束语

本文分析了PEG算法结合分块准循环矩阵构造校验矩阵的方法、QC-LDPC快速编码的实现策略以及改进型变量因子最小和译码算法，并对它们进行了相关性能分析比较。编解码部分的仿真性能对比可得：相比AWGN信道，本设计的LDPC码在标准S-V模型CM1场景的衰弱信道中，多损失至少1 dB的信噪。总之，PEG算法结合分块QC构造的校验矩阵，因其具有准循环结构，因此方便硬件存储及实现，变量因子最小和译码方式提供了译码参数调节的功能，有利于优化译码性能均衡信道衰弱，适合用于低发射功率下的IR-UWB系统。

［1］ Gallager R.Low density parity check codes［J］.IRE Transaction on Information Theory，1962，8（1）：21-28.

［2］ Chung S Y，Forney G D，Richardson Jr J，et al.On the design of low-density parity check codes within 0.004 5dB of the Shannon limit［J］.IEEE Comm，Letter，2001，5（2）：58-60.

［3］ Mu Liwei，Liu Xingcheng.Construction of binary LDPC convolutional codes based on finite fields［J］.IEEE Communication Letters，2012，16（6）：897-900.

［4］ Yin Huarui，Wang Zhengdao，Ke Lei，et al.Monobit digital receivers：Design，performance，and application to impulse radio［J］.IEEE Trans on Communication，2010，58（6）：1695-1704.

［5］ 张朝霞，王华奎.跳时 Reed-Solomon码的超宽带多址接入方式［J］.太原理工大学学报，2012，43（2）：119-122.

Zhang Zhaoxia，Wang Huakui.The multiple access of ultra-wide band based on reed-solomon codes［J］.Journal of Taiyuan University of Technology，2012，43（2）：119-122.

［6］ Haniffuddin H，Mohammad R，Mansor W.A review of turbo coding with channel estimate for single input single output system in ultra-wideband channel［C］／／8th IEEE International Colloquium on Signal Processing and its Applications.Hong kong：IEEE，2012：528-532.

［7］ Nyembezi N，Wasim Q.M.Concatenated RS-convolutional codes for ultra-wideband multiband OFDM ultra-wideband［C］／／IEEE 2006International Conference on Ultra-Wideband.Waltham，MA，USA：IEEE，2006：137-142.

［8］ Sung-Woo C，Sang S.RS decoder architecture for UWB ［C］／／8th International Conference on Advanced Communication Technology.Phoenox Park：IEEE，2006：808.

［9］ Peng Xiao，Zhao Xiongxin，Xie Qian.A macro-layer level fully parallel layered LDPC decoder SOC for IEEE 802.15.3capplication［C］／／2011International Symposium on VLSI Design，Automation and Test.Hsinchu，Taiwan：IEEE，2011：1-4.

［10］Hu Xiaoyu，Eleftheriou E.Regular and irregular progressive edge-growth tanner graphs［J］.IEEE Trans on Information Theory，2005，51（1）：386-398.

［11］Wang Yuliang，Ping Gong.An improved construction method of QC-LDPC codes based on the PEG algorithm［C］／／2011 Third Pacific-Asia Conference on Circuits，Communications and System.Wuhan：IEEE，2011：1-4

［12］Andreas F M.Channel models for ultra-wideband personal area net-works［J］.IEEE Wireless Communications，2003，10（6）：14-21.

［13］徐鹰，卫国.基于FPGA的 QSBC-LDPC码编码器的设计与实现［J］.数据采集与处理，2008，23（6）：713-717.

Xu Ying，Wei Guo.Design and implementation of QSBC-LDPC encoders based on FPGA［J］.Journal of Data Acquisition and Processing，2008，23（6）：713-717.

［14］Alfa A S，Jun C.Hybrid linear programming based decoding algorithm for LDPC codes［J］.IEEE Trans on Communications，2011，59（3）：740-749.

［15］徐鹰，卫国，朱近康.一种基于最小区域选择的LDPC码迭代译码算法［J］.中国科学技术大学学报，2008，38（12）：1365-1371.

Xu Ying，Wei Guo，Zhu Jinkang.Min-zone selection decoding algorithm for LDPC codes［J］.Journal of University of Science and Technology of China，2008，38（12）：1365-1371.