振动相消的质点能量哪里去了？

梁德清

（广西南宁三中，广西 南宁 530021）

1 问题提出

高二下学期在校内进行“波的衍射和干涉”（人教版选修3-4第12章第2节）集体备课时，有位教师根据干涉减弱区的质点不振动（两相干波振幅相同情形），提出了一个问题：“振动相消的质点能量为0，那么它原来振动时具有的能量哪里去了？”看似平淡的问题，却激起了组内教师们的热烈讨论.讨论中出现两种观点特别引起笔者的注意，观点1认为：波的传播过程同时也传播能量，结合波的独立传播原理来看，两列波分离后仍能继续传播能量，因而振动相消的质点能量虽然为0，但并未凭空消失，而是仍然潜伏在这些振动相消的质点中，在适当的时候（比如两列波分离后）又可以释放出来.观点2认为：在两列波相遇的区域，能量的叠加遵循标量叠加，因而振动相消的质点能量不为0，而是单列波贡献能量的2倍.笔者认为，上述两种观点对波叠加在能量方面的认识都还比较模糊，而且都存在不同程度的错误.既然错误的认识存在于教师当中，就有必要对该问题进行认真的分析.笔者整理如下，供同行参考.

2 问题分析

鉴于问题是针对高二教材提出，所以这里的讨论局限于振幅相同的两列机械波发生干涉的情形，因而涉及驻波的能量问题.驻波是一种特殊的干涉现象，它由两列振幅相同、传播方向相反的相干波叠加而成.如图1所示，两列简谐横波相遇，实线波以v向左传播，虚线波以v向右传播，单列波的振幅为A.两列波在任意x处P点的波动方程分别为

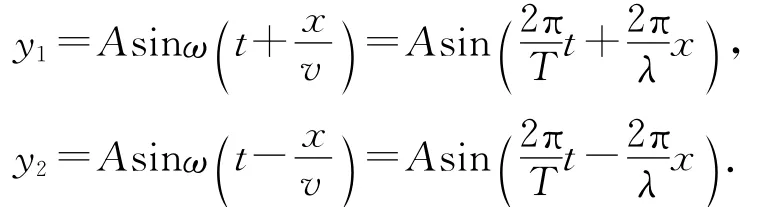
图1

合位移为

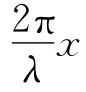
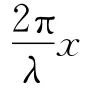
振动质点的能量由振幅来表征.仅存在单列波时，各处质点的振动能量相同，

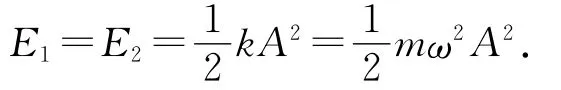
叠加后合振动的周期不变，合振动的能量与合振幅对应，

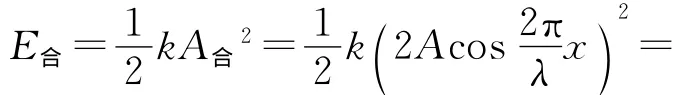
用图像表示单列波中各质点的能量分配如图2，两列波叠加后的各质点能量分配如图3.

图2

图3

3 结论

根据以上对两列振幅相同、传播方向相反的相干波叠加（驻波）的分析可得以下几点结论：

（1）两列波相遇区域内某质点的总能量并非简单地按标量相加E合＝E1＋E2＝2E1，而是遵循以下三角函数变化，

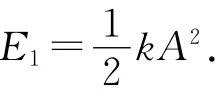
（2）叠加后振动相消及其附近质点的能量“自动”地分配到振动相长及其附近质点处，其中振动相消的质点能量为0，振动相长的质点能量最大.因而上述观点1承认振动相消的质点能量为0，但找不到其能量去向何方，胡乱地解释为能量仍潜伏在这些振动相消的质点中，在适当的时候又可以释放出来，这种说法是很荒谬的，能量（这里指机械能）为0就是没有了，它不能潜伏成为某种神秘的东西.观点2也找不到振动相消的质点能量去向何方，盲目地搬出标量叠加原理，认为叠加后其能量是单列波贡献能量的2倍，也是违背事实的.

（3）微观上看，质点间能量的重新分配是通过质点间的相互作用力做功来实现，其做功过程对某质点而言机械能不守恒.

例如振动相消的质点M，如图4.当只有实线波引起M振动时，M的机械能守恒.假如某时刻M正在经过平衡位置向上振动，其所受回复力为0.一旦虚线波恰好在该时刻传到M点，M点就成为虚线波的波首，在M点靠近虚线波源一侧的邻近质点对M施加向下的作用力，欲将M向下带动，如图5（注：图5可以设想为从图4将时间倒退T/4而得到）.综合两列波的贡献，M点的实际速度由原来单列波引起的最大振速vmax迅速减为0，从而使M点瞬间成为振动相消的质点，此过程邻近质点对M的作用力做负功使M的机械能损失，

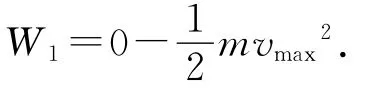
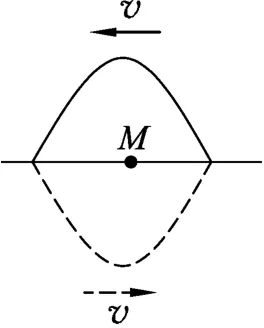
图4

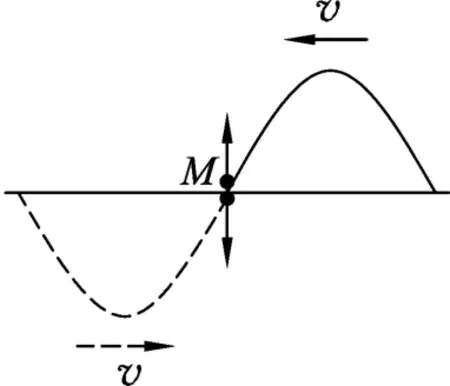
图5

图6

又如振动相长的质点N，如图6.在实线波中N经平衡位置向下振动，虚线波恰好传到N，邻近质点对N的作用力向下.综合两列波的贡献，N点的实际速度由vmax迅速增为2vmax，在使N成为振动相长质点的瞬间邻近质点的作用力做正功，使N的机械能增加，

（4）宏观上看，两列波叠加后大量质点获得的总能量等于两列波中所有质点的能量之和，且遵守能量的转化和守恒定律，

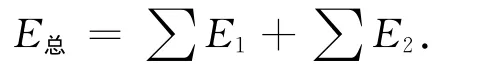
这一点很容易理解，因为整体而言质点间相互作用力为弹性内力，属于一种保守力，它改变了质点原有能量的平均分配，但不改变整体由波源处获得的总的机械能.

4 结束语

关于“波的衍射和干涉”一节，现行中学教材（人教版）对其中能量问题没有进行相关的讨论，对驻波也不做要求，因此本文提出的问题属课堂内容的延伸.我们可以从波的叠加原理出发，写出质点合振动的方程，从而确定叠加区域内质点的能量分配情况，再结合做功、能的转化和守恒定律弄清为什么这样分配，正所谓知其然，还要知其所以然.从系统的、联系的观点出发进行分析，将会使问题得到合理的解释.教师的备课固然要备教材、备课堂，往往还要备教材和课堂以外的内容，有时单靠个人的能力会突显不足，甚至会出现对某些问题在认识上的错误.通过集体备课，我们可以充分发挥团体的力量，既能教给学生更多的知识，又能提升自己的专业水平.

1 程稼夫.中学奥林匹克竞赛物理教程（力学篇）［M］.合肥：中国科学技术大学出版社，2002，12.