离散变量复合形法荷载试验优化设计研究

杨美云，陈生华

(广西壮族自治区交通规划勘察设计研究院，广西 南宁 530029)

离散变量复合形法荷载试验优化设计研究

杨美云，陈生华

(广西壮族自治区交通规划勘察设计研究院，广西 南宁 530029)

采用连续变量复合形法对桥梁荷载试验进行优化布载设计研究，可实现以车辆布载位置、行驶方向、车辆类型及占用车道数等作为设计变量的有约束优化分析。但连续变量复合形法只以车辆布置位置为连续变量，其他为离散性变量，为此，文章引入离散变量复合形法，开展桥梁荷载试验优化设计研究。通过计算实例分析，验证了离散复合形法对桥梁荷载试验车辆优化布置问题分析的适用性、准确性及求解的高效率性。

离散变量；复合形法；荷载试验；优化设计

0 引言

在文献[1]中笔者采用连续变量复合形法对桥梁荷载试验(静载试验)中的车辆自动化布置问题，进行了优化设计研究，并建立了以车辆布置位置、车辆行驶方向、车辆类型和占用车道数为设计变量，以非加载截面加载效率不超标及每排车之间的最小布置距离为约束条件，以加载截面效率和车辆总数为目标函数的有约束优化数学模型。笔者主要采用圆整法将离散变量进行连续化处理，最终得以按连续变量复合形法进行优化设计研究，最终通过一定的实例对该模型进行了验证。但是，在上述所选择的设计变量中，只有车辆布置位置可看成连续变量，而车辆行驶方向、车辆类型和占用车道数等实际上由一个个离散的点组成，属于离散变量。为进一步了解复合形法对桥梁静载试验车辆优化布置的适用性、准确性及效率性等，笔者针对荷载试验的连续与离散混合设计变量问题，进一步引入了离散变量复合形法在桥梁静载试验优化设计中的研究。

连续变量复合形法与离散变量复合形法的宗旨，都是寻找能使设计的目标函数值下降的最低点。然而，离散变量复合形法在处理离散和连续混合离散问题时，在算法上作了相应的改变。

1 离散变量复合形法

本文在原有连续变量复合形法的基础上，对离散复合形初始顶点的生成问题，作了相应修改。

(1)拟定一个初始离散点X(0)，确保X(0)中的每个分量都处在变量值的边界条件要求范围内，但不一定满足约束条件的初始值。

(2)将由初始复合形顶点生成的目标函数值进行排序，产生出：最好点X(L)、最坏点X(h)，计算除最坏点外所有点的中心点。采用离散一维搜索，即：将最坏点与除最坏点外所有点的中心点的连线方向定为离散一维搜索的方向，最坏顶点作为搜索基点。令离散一维搜索所得新点为X(t)，详细过程如下：

(1)

(2)

Si——离散一维搜索方向，可按下式计算：

(3)

(4)

(5)

离散一维搜索的关键是如何根据初始计算的新点与最坏点间的大小关系，不断调整搜索步长因子α的取值，使产生的新点不断小于最坏点并替换最坏点，直到α<αmin(最小有用步长因子)，即可结束离散一维搜索。αmin按式(6)计算：

(6)

式中：εi——连续变量给定精度值。

(3)将约束条件转化为目标函数的一部分，避免了在求解的过程中必须时刻保证设计变量满足约束条件的问题。在此主要采用分段函数理论，由于落在可行域内或可行域外的设计变量对应着不同的目标函数，据此，离散复合形法的目标函数，可由两段组成，即：有效目标函数EF(X)为：

(7)

式中：D——离散复合形的可行域；F(x)——离散复合形目标函数；M——数量级比F(X)大很多的常数；Gu(X)——可行域外的函数值，u=1，2，…，m。

最终求得最优解X*时有：

EF(X)=F(X)

(8)

即从有效目标函数已经转变为原目标函数。

最终，离散复合形算法调优迭代终止准则。迭代一定次数后，离散复合形各顶点的设计分量不再产生显著变化，即离散复合形各顶点的离散分量的最大分量值与最小分量的差值，不应大于一个离散增量Δi；连续分量的最大分量值与最小分量之差不大于一个较小的拟增量εi。

预先给定一个正整数EN，一般取n/2≤EN≤n，令RN为Li≤Δi(orεi)的个数，若有RN≥EN时，终止离散复合形的迭代运算。

2 基于离散变量复合形法的荷载试验车辆布置优化设计数学模型

2.1 设计变量

桥梁静载试验中，以车辆布置位置Xi，车辆行驶方向Di，车辆类型Ti，以及试验所占用车道数Li为设计变量：

(9)

(i=1，2…，nc)

式中：nc——荷载试验所用车排数；

由式(9)可知车辆布置位置Xi，车辆行驶方向Di，车辆类型Ti中又分别包含i个设计分量，所以，可知设计变量的维数n为：n=4·nc。

变量边界的取值如下：

2.1.1 车辆位置

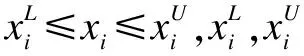
2.1.2 占用车道

0≤Li≤(3，4，…，8，…)，上限值由试验桥梁实际设计车道数Lane决定。

2.1.3 行驶方向

-1≤Di≤1，Di=-1or1的整数，当Di=-1时表示车辆逆向行驶，当Di=1时表示车辆正向行驶。

2.1.4 车辆类型

2≤Ti≤3；Ti(整数)为2or3轴车。

2.2 有效目标函数

桥梁荷载试验，实际上是一个满足加载效率指标的多维约束非线性优化问题：

(10)

式中：Si——相邻两辆车的最小间距值，取值通常为5m以上。

η=0.95～1.05，当加载效率值=1.0时目标函数最小，将上述问题转化为求解离散变量复合形法优化问题，可得如下有效目标函数：

(11)

式中：车在桥上时ri=1；车不在桥上时ri=0。因为在试验时不能确保所有车辆都在桥上，都是有效车辆，所以有必要引入此系数。

2.3 连续变量的拟离散化处理

荷载试验中的设计变量只有车辆布置位置Xi是线性变化的，取值是连续的；其它三类设计分量都是非线性的，其取值都对应有相应的离散点。车辆行驶方向Di有正向和逆向之分，不同的方向就变成了不同的离散值点，当车辆正向行驶时Di所对应的离散值可令为1，逆向时可令为-1；用于试验的车辆类型往往有两轴车和三轴车之分，所以Ti所对应的离散值域为2，3；每一个试验车列所占用的车道数，就决定了车道分布数Li的离散值，当桥梁设计车道数为3车道时，Li可取的离散值域为：0，1，2，3；当桥梁设计车道数为4车道时，Li可取的离散值域为：0，1，2，3，4；对于不同的车道数按上述类推。

车辆布置位置Xi作为连续变量，还需对此进行拟离散化处理。连续变量的拟离散化处理的关键是确定离散后的离散值之间的最小间距ε，都知道荷载试验中桥梁长度习惯取“米”为单位，在此为了使计算更精确，离散增量ε可取较小的单位，在离散化的处理中考虑取分米为单位，取值结束后可根据需要再把长度单位转化为想要的单位即可，取ε=1dm，根据车辆布置位置Xi的上下限值可以计算出车辆位置Xi的离散值域。

由以上可确定，离散变量的间隔为：(1，1，1，1)。

3 实例计算与结果分析

笔者以某五梁装配式钢筋混凝土简支梁桥为计算实例，荷载：公路-Ⅰ级，19.50m的计算跨径，主梁翼缘板采用刚性连接的连接方式[2]。该简支梁桥主梁采用C40混凝土，弹性模量E=3.25×1010N/m2，主梁跨中截面的惯矩为Ic=0.066 26m4，结构基频为f1=4.187Hz；对于该5片T梁组成的简支梁桥，在研究荷载试验对桥梁结构内力的影响效应时，只需任取一片梁进行研究即可。故本文在此只选取了边主梁作为试验的加载对象进行研究，应用Midas有限元程序计算得到结构的冲击系数为μ=1.262，建立边主梁单跨有限元模型，共建立19个单元20个节点，主桥静力加载控制截面位置简图如图1所示：

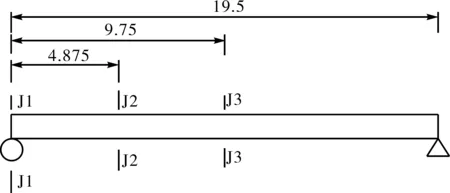
图1 加载控制截面位置简图(单位：m)

给定离散复合形法的参数值，初步拟定试验所需车排数nc=5；桥梁左右延伸一定长度LS=25m；设计车道数Lane=2车道；复合形顶点个数k=n+1=4·nc+1=4×5+1=21；离散一维搜索步长α=1.3；终止系数：EN=k-1=21-1=20。

多片简支梁桥在计算主梁内力值时，要考虑结构的横向受力，所以在按照程序进行优化计算时，必须考虑荷载横向分布系数的作用，所计算的内力值必须先进行横向折减计算。可得到如下各工况的优化计算的最优效率值及分布情况，具体结果如表1～3所示。

表2 各工况下对应的效率值汇总表

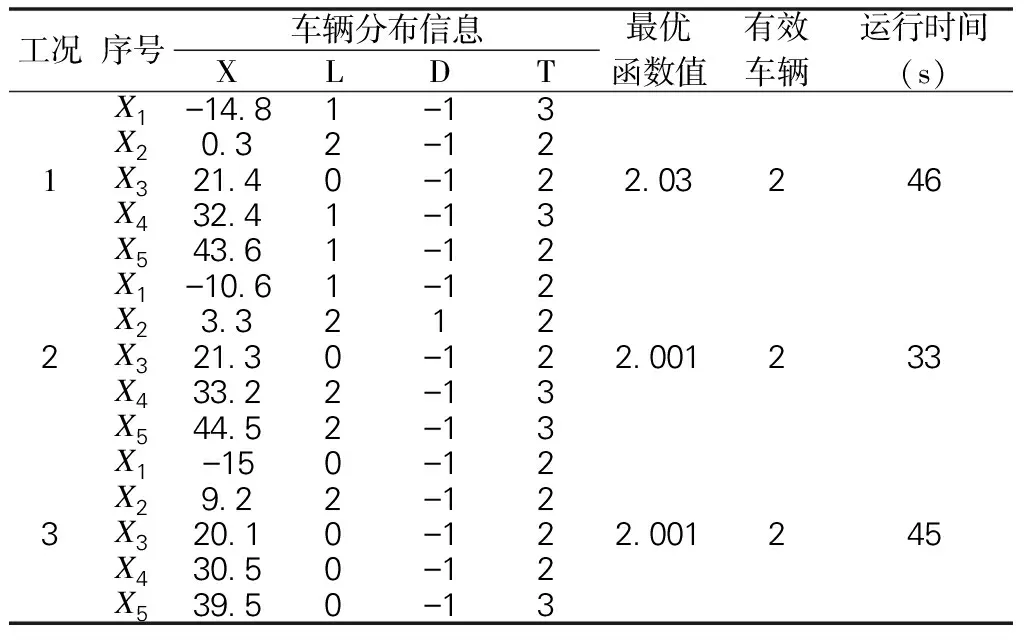
表3 各工况下对应的加载优化分布信息表

由上述1～3表可见，3个工况下的效率值都能满足0.95～1.05的要求，且非控制截面都能确保效率值≤1.05，同时每个工况下的运行时间都≤1min，计算时间较快。

4 结语

文献[1]基于连续变量复合形法建立了荷载试验车辆布置优化设计数学模型，模型中包含车辆布置位置、行驶方向、车辆类型和占用车道数等设计变量，并采用圆整法对后三个离散设计变量进行连续化处理，最后完成优化设计研究。

本文在连续变量复合形法对桥梁荷载试验中车辆自动化布载问题的分析优势上，提出采用离散变量复合形法对该问题进行更深入的研究，从而实现复合形法对离散性的优化设计变量的处理，体现出该方法优良的适应性。

[1]王小松，杨美云，陈 斌.基于复合形法的荷载试验车辆布置优化设计[J].重庆交通大学学报(自然科学版)，2014.6：18-21.

[2]杨美云.桥梁静载试验加载方法研究综述[J].科技创新与应用，2013.23：208.

[3]朱伯芳，黎展眉，张璧城.结构优化设计原理与应用[M].北京：水利电力出版社，1984.

Study on Load Test Optimization Design of Discrete Variable Complex Method

YANG Mei-yun，CHEN Sheng-hua

(Guangxi Communications Planning Surveying and Designing Institute，Nanning，Guangxi，530029)

The optimization load distribution design study on bridge load test by using the continuous variable complex method can achieve the constrained optimization analysis with the vehicle load distribution location，driving directions，vehicle type and occupancy lanes as the design variables.However，the continuous varia-bles complex method can only take the vehicle distribution position as the continuous variable，all others are the discrete variables，thus this article introduced the discrete variable complex method to carry out the bridge load test design optimization studies.By practical computing analysis，it verified the applicability，accuracy，and high solving efficiency of discrete complex method on the vehicle layout optimization problem of bridge load test.

Discrete variables；Complex method；Load test；Optimization design

U441+2

A

10.13282/j.cnki.wccst.2015.04.019

1673-4874(2015)04-0066-04

2015-03-07

杨美云，硕士，主要从事桥梁工程设计工作。