对短公钥的基于身份数字签名算法的安全性攻击*

郑 红， 范 佳

(1.四川九洲空管科技有限责任公司，四川 绵阳 621000;2.保密通信重点实验室，四川 成都 610041)

0 引言

1984年Shamir[1]提出了基于身份的密码体制。在该体制下，用户的公钥是用户的身份信息，如email地址、身份证号码和员工工号等;并且用户的私钥是由一个可信的第三方，称为私钥生成中心(private key generator，PKG)的机构来产生。因为基于身份的密码系统不需要使用数字证书，因此可以避免传统的公钥密码系统(基于PKI的公钥密码系统)建立和管理公钥基础设施的代价。

2001年，Boneh，Shacham和Lynn(BSL)提出了基于双线性对的数字签名[2]。双线性对运算使得BSL方案不仅签名非常短，而且构造简单，验证也非常方便。但是BSL签名方案只能在随机预言机模型下提供可证安全分析。2006年，Paterson和Schuldt(PS)同样基于双线性对，构造了第一个可以在标准模型下证明安全的基于身份数字签名算法(简称为PS算法)[3]。PS算法是Waters签名算法[4]的扩展，直接使用了两次独立的Waters身份处理函数，所以其效率并不高。最近几年密码学者们一直在为提高这个算法而努力。2009年李继国等[5]提出一个对PS数字签名算法的一个改进方案。改进后的方案在计算效率上有所提高，主要体现在验证签名时，改进算法的计算量比PS算法减小了三分之一。2011年王之怡等人[6]对李继国等的算法进一步进行改进，提出了一种短公钥的基于身份的数字签名方案，该方案声称其通过改进参数选择，从而大大减少了公钥参数数量。2013年黄斌和邓小鸿[7]对李继国等设计的方案[5]成功进行了攻击，使得攻击者能够构造任意ID的用户私钥。

本文将对王之怡等人提出的短公钥的基于身份数字签名算法进行安全性攻击。

1 签名算法回顾

王之怡等人设计的短公钥的基于身份的数字签名算法共包含如下四个算法，算法描述如下:

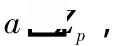
(2)私钥提取DerMSK(ID):TA随机选择r∈Zp，计算身份为ID的用户私钥为:

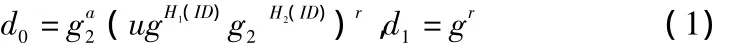
(3)签名SMPK(dID，M):身份为ID的签名者首先进行一个随机化处理得到

紧接着，身份为ID的签名者随机选择t∈Zp，生成对消息M的签名 σ ={σ0，σ1，σ2}为:

(4)验证 VID(M，σ):令(M，σ0，σ1，σ2)为收到的签名，验证者验证等式:

若该等式成立，则签名合法，否则为非法签名。

2 对该签名算法的攻击

该算法的设计者宣称该算法满足以下安全性:令H1，H2，H3，H4是抗碰撞Hash函数，假设在双线性映射群中计算Diffie-Hellman(CDH)数学难题成立，那么该算法是能抗适应性选择消息伪造签名攻击(UCMA)的。

UCMA安全性定义如下的攻击游戏来描述。该攻击游戏由一个挑战者和一个攻击者来完成。该游戏包含如下三个阶段:

第一阶段:挑战者运行Setup(1k)获得主公私钥对(MPK，MSK)，并将主公钥MPK发送给攻击者;

第二阶段:攻击者适应性地进行以下两种询问。

(1)私钥提取询问:攻击者提交身份ID给挑战者，挑战者使用主私钥计算dID=DerMSK(ID)，并将进行应答;

(2)签名询问:攻击者适应性地选取身份和消息{ID，M}进行签名询问，挑战者首先生成身份对应的私钥dID=DerMSK(ID)，进一步使用dID生成签名，最后返回签名结果;

第三阶段:攻击者输出{σ*，M*，ID*}，要求攻击者未询问过身份ID*的私钥且未询问过{M*，ID*}的签名，如果攻击者输出的签名能通过验证，那么攻击者攻击成功。

UCMA安全性定义:如果任何概率多项式时间攻击者在以上游戏中攻击成功的优势∈(其中∈=|Pr[攻击者攻击成功]-1/2|)可以忽略，则称一个基于身份签名算法是UCMA安全的。

以下将通过两种攻击说明该算法并不满足以上的UCMA安全性。

攻击1:具体的攻击步骤如下:

(1)在 H2中寻找碰撞(ID1，ID2)满足 ID1≠ID2，H2(ID1)=H2(ID2):注意到在算法中描述时只提到H2:{0，1}*→Zk1，并没有明确k1的大小。在后面的安全性证明的过程中才确定k1=1+qE，(其中qE为攻击者在攻击游戏中进行签名询问的次数，qE=230)。目前一台普通的单机(2.93G双核CPU，4G内存)运行一次SHA-1的时间大约为2-22秒，运行230+2次运算的时间为128秒。假设H2运行时间与SHA-1时间相当，在H2中找到一个碰撞的时间至多为128秒(由于k1=230+1，运行230+2次H2，必然会找到一个碰撞)。

(2)攻击者通过私钥询问获得ID1的私钥:

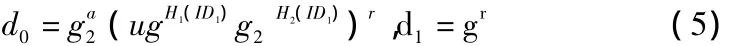
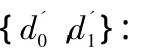
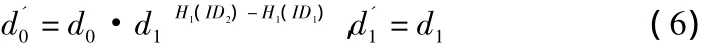
可以很容易地验证

(4)由于此时攻击者已经掌握了身份为ID2的用户的合法私钥，因此可以伪造该用户的所有签名。

攻击2:具体的攻击步骤如下:

攻击者通过找寻H4的碰撞((M1)，(M2))满足M1≠M2，H4(M1)=H4(M2)。通过询问某个ID对消息M1的签名，可以构造该ID对于M2的签名。

3 结语

本文对一个具有短公钥特征的基于身份的数字签名算法进行了安全性分析，发现其并不满足其所

声称的安全性——抗适应性选择消息伪造签名攻击。本文的第一种公钥针对用户私钥。在该种攻击下，攻击者如果获得某个用户私钥，则他可以计算系统内所有其他用户的合法私钥。本文的第二种攻击针对签名伪造。在该种攻击下，攻击者如果获得了某个用户的一个合法签名，则他可以伪造该用户对任意其他消息的合法签名。

[1] Shamir A.Identity-based Crypto Systems and Signature Schemes[C]//Advances in Cryptology-Crypto'84.Berlin:Springer-Verlag，1984:47-53.

[2] Boneh D，Shacham H and Lynn B.Short Signatures from the Weil Pairing[J].J.of Cryptology，2004，17(4):297-319.

[3] Paterson K，Schuldt J.Efficient Identity-based Signatures Security in Standard Model[C]//Advances in Cryptology Proceedings of ACISP 2006.Berlin:Springer-Verlag，2006:207-222.

[4] Waters B.Efficient Identity-based Encryption Without Random Oracles[C]//Proc.of Eurocrypt'05，Berlin:Springer-Verlag，2005:114-127.

[5] 李继国，姜平进.标准模型下可证安全的基于身份的高效签名方案[J].计算机学报，2009，32(11):2130-2136.

[6] 王之怡，刘铁，康立等.短公钥的可证明安全基于身份数字签名算法[J].计算机科学，2011，38(3):136-139.

[7] 黄斌，邓小鸿.高效的基于身份签名方案的安全性分析[J].计算机应用，2013，33(1):168-170.