环状电极诱导的静电场电位分布研究

王韶霈，宋开宏，谢国大，黄 帅

（安徽大学 电子信息工程学院，安徽 合肥 230601）

0 引 言

在电磁场工程问题中，静电场和时谐场的场分布是电磁场工程设计首先要解决的问题，因为它直接关系到整个系统的性能是否满足实际要求。随着对静电现象研究的日益深入，对静电场中场强和电位分布的了解也更加迫切。随着通信业、航空航天业的发展，对高空中电离层的研究有着重要的意义。电离层作为一种传播介质会使电波损失部分能量，对通信造成一定影响。就以上问题，需要在地面建立带有电极的真空罐［1］对其进行模拟仿真，观察研究其特性。对真空罐的研究也要先从静电场做起，对静电场进行研究就需要通过描绘出其电位分布来具体分析。

在电磁场数值分析计算方法中，有限差分法一直是一种重要的数值方法。静电场中电位函数满足拉普拉斯方程，通过给定的边界条件求解拉普拉斯方程，最终得到静电场内的电位分布图以及电场图。在对待二维静电场问题中运用有限差分法求拉普拉斯方程数值解时最为经典是运用五点差分格式。对待三维静电场问题时会应用到七点差分格式，若所求区域为轴对称，七点差分格式可以转化为五点差分格式。这种利用离散节点与周围四个节点的关系迭代求解电位值的方法很适合在EXCEL上完成。本文从五点差分格式出发，运用EXCEL计算真空罐里的静电场的电位数值，联合MATLAB的图形功能，绘制静电场等位线，形象直观掌握真空罐中的场分布，为工程设计奠定基础。

1 理论分析

柱坐标下的拉普拉斯方程有以下形式：

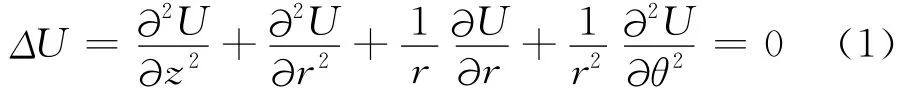
设空间中任意一点为U（z0，r0，θ0），根据有限差分法［2］，取圆柱等间距网格高Δz＝h，半径Δr＝k，角度Δθ＝τ。设：

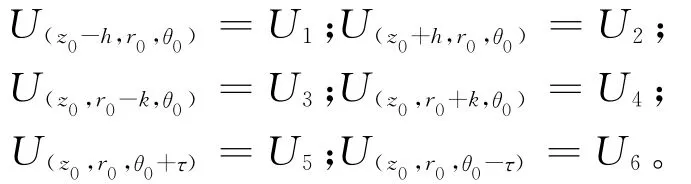
圆柱坐标系中三维拉普拉斯方程的七点差分公式［3］：

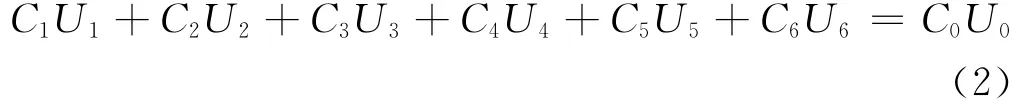
其中：

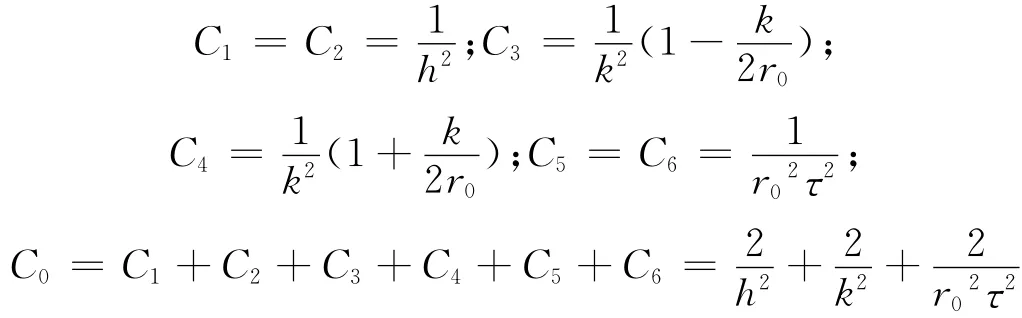
C0、C1、C3、C4、C5、C6是取决于步长的已知系数，U0、U1、U2、U3、U4、U5、U6则是待求的未知数。

待求区域如果具有对称性，这个区域内各点的电位函数值也与角度θ无关，且介质均匀，则式（2）有关对应角度θ的项就可不用考虑，那么七点差分方程就可简化为五点差分方程：

而r0＝0处即对称轴上，式（3）不适用，对称轴上的点系数为：

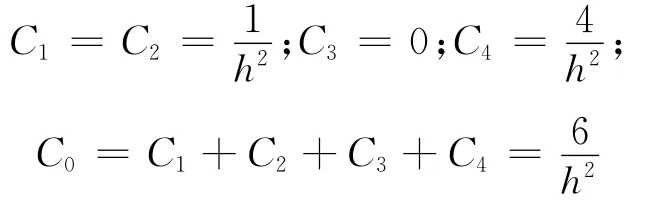
从式（3）可看出，转化后的公式计算仅在rz平面，就位于rz平面内的轴对称平面而言，它的场域离散化下的网格划分与离散点分布方式与二维场中的讨论相同。在轴对称场中，网格在空间的延续分布，即是关于轴对称的一系列回转体。

2 实际工程问题的计算机解法

2.1 具体问题

在一个直径为70 cm、长度为180 cm、两端为半球的真空罐内，在其轴心中间对称、间距为60 cm的位置放置两个环形电极，电极上环形电极的直径为4 cm，不考虑电极环的厚度尺寸，真空罐按接地处理，环状电极施加电压信号为10 V，计算真空罐内部空间的电场分布。

2.2 问题的解决

真空罐内空间是具有对称性的，且介质均匀，根据以上理论分析可以将这个三维问题转化为二维问题，只计算分析真空罐一个截面里的电位分布，根据（3）式，用高斯—赛德尔迭代法［4］计算，公式为：

2.2.1 选取计算工具

根据式（4）可以看出，在数值求解时通常需要编程计算机完成大规模递推关系，必须求解大型多元方程组，计算量庞大，给应用中造成很大的不方便。EXCEL表在数值计算中有很大的应用潜能，公式的复制十分突出地显示出它的递推运算优势，特别是“重复计算”功能可十分简便地处理一些复杂递推关系的数值计算，一般应用软件无法比拟。根据五点差分格式以及计算过程中需要多步迭代的特点，EXCEL在计算上有很大的优势，选择［5，6］其为计算工具。

2.2.2 网格剖分

根据已知条件，本文在EXCEL中取71行与181列，同时要对真空罐截面的边缘进行数字化。圆弧边缘作以下处理：取EXCEL中两行36列单元格，从A1单元格依次输入0～35，再在B1单元格中输公式“35＋（35＾2－（A1－35）＾2）＾（1／2）”，将B1单元格的公式复制到后面35个单元格中，再对通过公式得到的数据四舍五入取整，最终获得以（35，35）为圆心，35为半径圆的四分之一圆边在EXCL的坐标，然后通过对称关系补齐真空罐截面另外的圆弧边界。

2.2.3 计算结果

剖分完成后的一个单元格即代表求解区域的一个节点，而单元格里的值就是该节点的电势，这时就需要确定边界条件，将真空罐罐体上的单元格都输入数值0。由于电极厚度不计，则其在截面上可用2个点来表示，把代表两个电极位置的单元格找到，输入数值10。真空罐以外的单元格统一输入数值0。

确定了边界条件，需要输入公式进行计算。根据式（4），则每列的C3、C4是不同的，取决于r0，需要逐行输入公式从对称轴I，r0＝0开始，每向上或者向下一行r0的值加1。逐行输入公式时，选中需要输入公式的一行，再选中本行其中一个单元格输入相应的公式，然后再选中这个单元格，复制，按住Ctrl键拖拽选取包含本行里的其他单元格，不要选中已经输入边界条件的单元格，最后粘贴。进行迭代计算，打开“工具”菜单下的“选项”，选择“重复计算”，将“迭代计算”选中，设置“最多迭代次数”为3 000，最大误差为0.001，点击“确定”，通过一段时间的迭代计算，得出结果，这时可以很直观地看出计算结果。

由于EXCEL绘图功能有限，而MATLAB拥有强大的绘图功能，能弥补绘图上的这一缺点，所以在数据到图形的处理工作上，本文将选用MATLAB软件来进行。打开MATLAB，利用文件菜单下的“Import data...”将EXCEL中计算得到的最终数据导入MATLAB，将导入的数据名定义为A。再用contour函数绘制等位线，在命令窗口输入：contour（A，11），绘制了11条等位线，每条等位线间隔为1 V，这样就得到了真空罐一个离散截面的电场等位线图。

2.3 结论验证

MATLAB是一种功能十分强大、运算效率很高的专业计算机软件，它已经成为一种极其灵活的计算机体系，具有简单易学、短小高效的源代码，丰富的内部函数等优点。本文选用MATLAB对真空罐进行仿真，并对结论进行验证。同样以式（4）为计算的基本公式，编写程序并画图，得到了真空罐里的电位仿真图，与运用EXCEL计算得到的最终电位图作比较分析，结果一致。

3 结 论

本文将有限差分法运用到解决实际工程问题中，这种以有限差分法为核心理论的方法相当于一种仿真模拟软件。它在计算二维静电场问题上受到的条件限制不多，只要网格剖分足够精细，都能计算不规则边界的静电场问题。而在三维问题上目前只能计算轴对称场的工程问题，所以在计算三维问题时还是有很大的局限性。虽然如此，但对EXCEL的应用仍然有着方便快捷、计算结果以及通过它得到的图像直观明了、不需要编写程序的优势，在解决更多工程问题上还有很大的潜能等待开发。

用有限差分法代替偏微分求解电位函数，将二阶偏倒数运算转化为代数运算，使求解过程更加简单，再运用EXCEL作为计算工具得出结论的过程就更为简化。由于差分方程代替偏微分方程和差分方程本身的特点，在求解过程中存在一定的误差，所以在计算过程中要根据具体问题的精度要求选择合适的网格划分。而由于EXCEL里的单元格有限，并且在本文中用单元格描述真空罐的边缘时用的是四舍五入取整的方法，这就使得其精度上受到限制，最终根据数据处理得到的数据绘制的电位图不够精细，但仍然可以为实际工程中的快速计算提供参考。

［1］ Giuliano V，Michele D S，Franco G，Roberto B，Mario P.The INAF－IFSI Large Plasma Chamber［J］.INAF／IFSI，2010，（5）：1－5.

［2］ 谢处方.电磁场与电磁波（第4版）［M］.北京：高等教育出版社，2006.

［3］ 梁志辉.用差分法计算柱坐标系的拉普拉斯方程［J］.信息系统工程，2009，（3）：104－105.

［4］ 盛剑霓.电磁场数值分析［M］.北京：科学出版社，1984.

［5］ 贾新民，严 文.有限差分法求解拉普拉斯方程［J］.昌吉学院学报，2009，（5）：105－109.

［6］ 赵宣铭，赵玉怀.典型数学物理方程的Excel数值解法［J］.纺织高校基础科学学报，2009，23（1）：118－126.

［7］ 何红雨.电磁场数值计算法与 MATLAB实现［M］.武汉：华中科技大学出版社，2004.

［8］ 葛 超，王 蕾，曹秀爽.MATLAB技术大全［M］.北京：人民邮电出版社，2014.

［9］ 张雅男，徐 飞，叶 颖.MATLAB模拟静电场与模拟静电场实验的比较［J］.物理与工程，2008，（7）：32－33.