基于改进遗传算法的泵站优化运行
2015-07-25杨建文李志鹏喻哲欣
杨建文,李志鹏,喻哲欣
(长沙理工大学能源与动力工程学院,410114,长沙)
随着科技的不断发展,变频调速装置技术的成熟,越来越多的泵站开始进行节能优化改造。但是,变频调速装置需要合理利用才能够达到节能优化的效果,否则适得其反。变频调速装置能够对水泵电动机的转速进行控制,具有调速范围宽、流量调节连续、显著降低节流损耗及启动水泵机组电动机时电流平稳等优点。目前很多泵站的节能改造都是添加变频调速装置,所以对泵站调速泵进行优化运行研究具有重要意义。调速泵站的优化设计是一种连续、离散变量混合的非线性规划问题研究,采用传统的线性规划法、动态规划法等进行计算效率低,得到的结果精度差。传统的遗传算法有“早熟”缺陷,本文提出了一种改进的遗传算法,来对泵站的优化运行模型进行求解。
一、数学模型的建立
1.水泵的特性曲线
泵站供水系统的优化模型是建立在水泵性能曲线基础之上的,所以首先要对水泵的特性曲线进行详细的描述。通常是对水泵的特性曲线进行曲线拟合得到水泵特性曲线的表达式。假设在一个供水泵站具有n台水泵,则在额定转速下第i台水泵的流量—扬程(Qi—Hi)的表达式表示为:
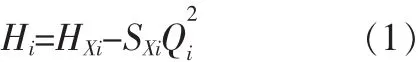
流量—功率(Qi—Pi)的表达式为:

式(1)和式(2)中,Qi为泵的流量(m3/s),Hi为泵的扬程(m),HXi为泵流量为零时的虚扬程(m),SXi为泵虚阻耗系数(S2/m5),Pi为泵流 量 轴功 率 (kW),ai、bi、ci为泵轴功率的拟合系数。
根据比例定律,水泵在调速率ki下的扬程和功率的表达式分别为:
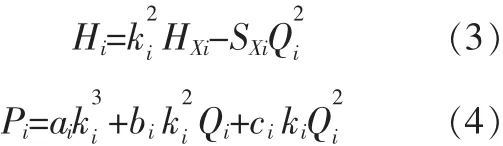
式(3)和式(4)中,ki为水泵的调速比。ki=ni/n0,n0、ni分别表示的水泵的额定转速与工作转速(r/min)。
2.水泵变速调节模型的建立
假设在一个供水泵站有n台水泵,其中m台水泵为变频调速泵,其余的水泵为定速泵。在满足供水流量和扬程的条件下,保证每台水泵能够在高效区运行,从而使水泵的能耗最低。所以需建立一个以运行水泵轴功率之和为目标函数的优化运行数学模型,如下式所示:

式中,ωi为水泵的开启状态,取值1或0(1 代表开启,0 代表关闭)。
为保证各水泵在高效区运行,约束条件为:
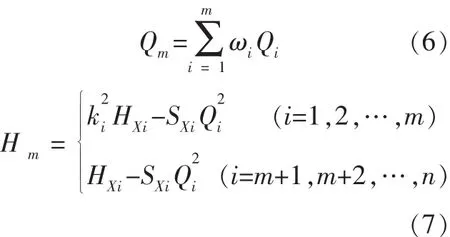
式(6)和式(7)中,Qm为供水要求的水量 (m3/h),Hm为供水要求的水压(m)。Kimin≤Ki≤1 (i=1,2,…,m)。Qimin≤Qi≤Qimax(i=1,2,…,n)。

图1 遗传算法运算过程
二、改进遗传算法设计
在上述建立的数学模型中,既包含连续变量(即水泵的转速),又包含离散变量(即水泵运行数量),约束条件中既有不等式又有等式约束,除此之外又受到水泵特性的非线性、多变量耦合因素的影响,采用线性规划、动态规划法都比较复杂。采用传统的线性规划法、动态规划法等进行计算,效率低且得到的结果精度差。遗传算法在搜索方式上具有很大的随机性,通过很多实践,证明遗传算法在供水系统优化设计中比较适用,能够得到全局最优解或者趋于最优解,但是传统的遗传算法也有不足,即“早熟”,所以本文采用改进的遗传算法求解泵站的优化运行模型。
1.遗传算法的运算过程
遗传算法运算过程,见图1。
(1)编码方法和种群规模
在建立的泵站优化模中,因同时包含离散和连续变量,所以采用二进制编码法对水泵的转速与运行水泵的数量进行编码。假设有2台变频调速泵运行,对应的调速比为k1、k2,然后通过8位二进制数对其进行编码。由于变频调速水泵的调速比低于0.5时,水泵的效率将大大降低,所以将0.5~1范围内的转速比分为256个区间,目的是为了能够达到更高的精度。对于水泵的开启状态,通过二进制位1和0进行表示 (1代表开启,0代表关闭)。
初始种群的数量一般是由随机数发生器产生,产生一定量的染色体,为了保证能够得到全局最优解染色体的数量 (一般为 30~200个),在本文当中种群的数量取100。
(2)确定适应度函数
记录适应度较大的N个个体,并依次进行选择、交叉、变异等操作,产生中间群体。
(3)交叉变异
种群的交叉操作是通过随机交叉运算,即随机选择两个父染色体进行交叉,产生一个随机数,将该随机数与设定好的交叉概率Pc进行对比,如果小于交叉概率,那么将两个父染色体交叉点右边部分进行交换,产生新的染色体。
种群的变异类似于种群的交叉操作产生一个随机数,将该随机数同设定好的变异概率Pm进行对比,如果小于变异概率Pm,那么对该染色体进行变异操作。变异概率Pm的取值范围一般为0.001~0.1之间。
2.遗传算法的改进
在遗传算法计算的过程中,交叉概率Pc和变异概率Pm对算法的计算结果影响较大。如果交叉概率Pc过大,那么就容易造成种群中高适应度的个体结构遭到破坏,如果交叉概率Pc过小,就容易造成整个搜索过程停滞不前;变异概率Pm过大,就会使遗传算法演变成了随即搜索算法,变异概率Pm过小,种群又很难产生新的个体,所以如何确定合理的交叉概率Pc和变异概率Pm对遗传算法的计算至关重要。在目前计算中,交叉概率Pc和变异概率Pm的选取都是通过反复的实验来找到最佳值。所以本文中提出了改进算法,将交叉概率Pc和变异概率Pm作如下设定:
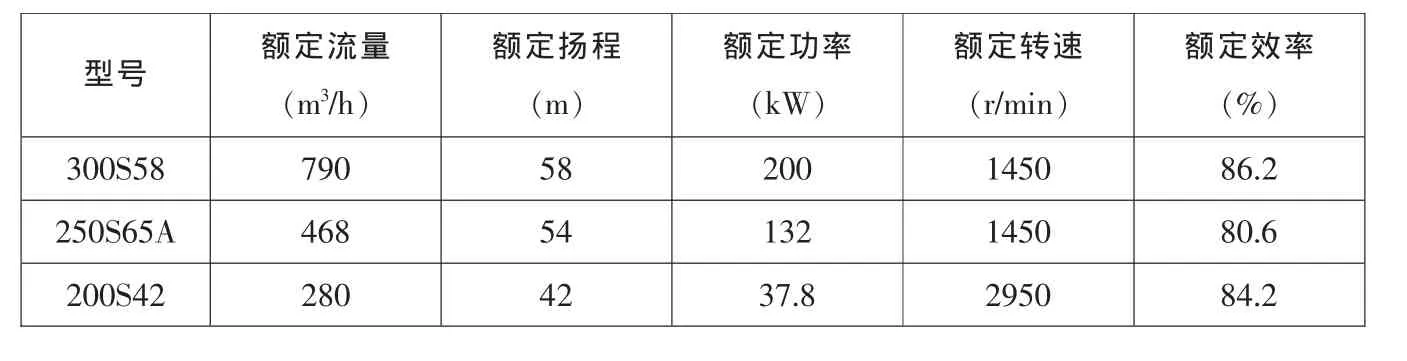
表1 泵站水泵参数
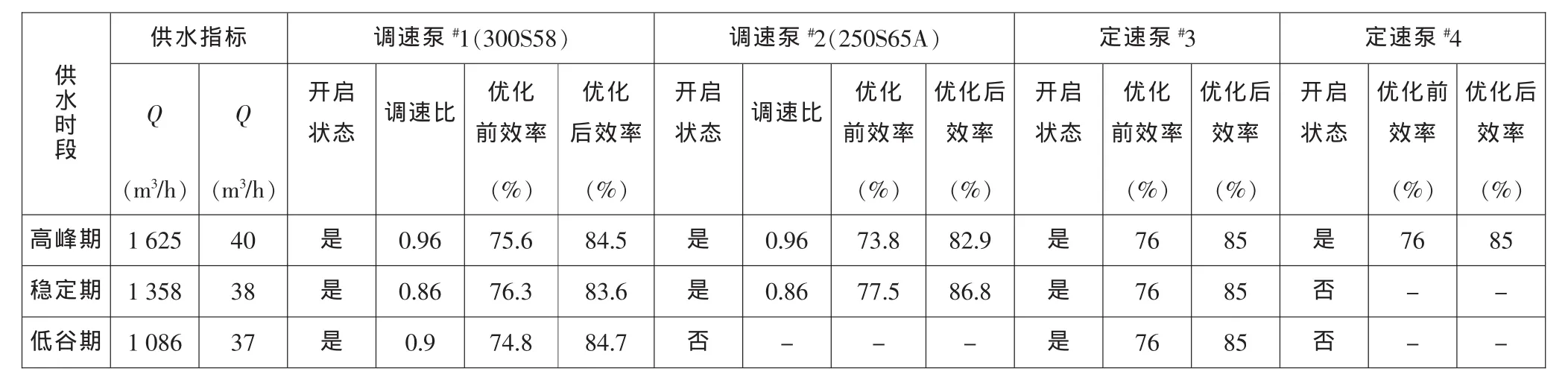
表2 优化前后泵站水泵运行状态

式(8)和式(9)中, pc1取 0.09,pc2取0.6,pm1取 0.1,pm2取 0.001;fmax为种群的最大适应度,favg为种群的平均适应度,f'为交叉的两个个体中适应度较大的值,f表示变异的个体适应度的值。
通过对交叉概率pc和变异概率pm的调整,对适应度比平均适用度低的个体,采用较大的交叉概率和变异概率,对适应度高于平均适应度的个体,采用相应的交叉概率和变异概率,通过对交叉概率pc和变异概率pm的调整能够有效改善遗传算法种群的个体质量,解决搜索停滞不前的问题。通过改进遗传算法的优化计算,大大改善了种群的多样性,解决了传统遗传算法中存在的“早熟”现象,跳出局部最优值,大大提高了解的质量。
三、某泵站供水系统工程实例
某供水泵站有型号300S58、250S65A调速泵各一台,型号200S42定速泵两台,该供水泵站春秋季节时每天最大的供水流量为1 753 m3/h,平均供水流量1 215 m3/h。每天6时到9时、12时到13时、18时到21时三个时段为供水高峰期,平均供水量1 625 m3/h;9时到 12时、13时到 18时两个时段为供水平稳期,平均供水量1 358 m3/h;21时到次日6时为供水的低谷期,平均供水量1 086 m3/h。供水泵站的水泵型号参数如表1所示。
采用改进后的遗传算法对该泵站的优化运行进行计算。首先将4台不同型号的水泵进行编码,共32位编码,种群的规模一般取100到200之间,本文取 150,交叉概率 pm取 0.09,pc2取 0.6, 变异概率 pm1取0.1,pm2取 0.001,迭代次数设定为100代。通过改进遗传算法得出的优化运行方案与改进之前的运行方案相比,水泵的运行效率提高了10%左右。优化前后水泵的运行情况见表2。
由表2可以看出,通过改进遗传算法计算得出的泵站水泵的运行效率比改进之前有较大提升。在满足供水流量、扬程等参数的基础上,对泵站内水泵运行进行合理优化,能够在很大程度上提高泵站的经济效益。优化之前水泵的平均效率在75%左右,通过改进遗传算法进行优化得出的水泵平均效率在84%左右。通过对比可以看出水泵的运行效率有了明显提升。优化结果表明,模型及求解方法有效,可适用于调速泵站的优化运行。
四、结 语
基于改进遗传算法的泵站节能控制,比传统的动态规划法计算更加快速,比线性规划法得出的结果更优,有效地解决了传统遗传算法中过早收敛等问题。改进遗传算法的搜索方式具有很大的随机性,通过实践证明对于任何供水系统的优化设计,能得到全局最优解或趋于全局最优的解。
基于改进遗传算法的泵站节能,能够适用于绝大多数泵站的优化运行。当供水状态发生变化时,能够根据运行数据迅速调整水泵的运行状态,使水泵的运行效率提高,从而达到泵站节能的目的。
[1]袁尧,刘超.基于SQP局部搜索遗传算法的泵站优化运行[J].农机化研究,2013(9).
[2]占龙杨,顾伯勤,邵春雷.基于遗传算法的多泵系统优化运行研究[J].煤矿机械,2011(10).
[3]仲云飞,梅一韬,等.遗传算法优化BP神经网络在大坝扬压力预测中的应用[J].水电能源科学,2012(6).
[4]张敏,陈谦,等.基于改进混沌遗传算法的配网重构 [J].水电能源科学,2013(5).
[5]王立.我国泵系统节能的现状及发展前景[J].水泵技术,2012(1).
[6]陈德强,马敬.供水泵站水泵节能改造及其效益分析[J].中国给水排水,2010(16).
[7]吴伯元,田晓蕾,张东胜.直接变换式高压变频器在城市供水中的应用[J].中国给水排水,2012(22).
