基于全寿命周期成本的配电网多阶段无功规划
2015-07-24陈丽侯晨伟张晋国
陈丽,侯晨伟,张晋国
(河北农业大学 机电工程学院,河北 保定 071001)
配电网无功规划是避免在配电网改扩建过程中盲目建设无功电源、降损节能、提高电压质量的有效手段之一.由于中长期配电网规划周期长,负荷需求逐步增长,为了以较少投资来满足负荷逐步增长需要,通常将规划分几个阶段进行[1].因此,在进行配电网无功规划时,若能综合考虑配电网多阶段无功需求水平,合理地安排无功补偿设备(动态无功补偿电容器)的安装时间和安装容量,既能克服短期无功规划易带来“无功补偿设备复拆”的浪费现象,又能克服长期无功规划资金投入大、运行前期设备利用率低的问题,从而实现配电网无功补偿设备在整个寿命周期的降损节能收益最大化.
配电网无功规划优化是一个多目标、多约束的非线性规划问题.近年来,配电网无功规划深受人们的重视.胡泽春等[2]以年度降损收益最大化为目标函数,建立了考虑多负荷水平的配电网无功规划模型.杨丽徙等[3]运用灵敏度分析法确定系统的无功电源补偿点,应用改进模拟树木生长算法求解无功电源的补偿容量,二者交互寻优求解.汪超等[4]以有功损耗功率最小为目标函数,建立了配电网无功规划数学模型,并用改进粒子群优化算法求解.朱勇等[5]以成本-效益比值和静态电压稳定指标为综合优化模型,建立了含异步风力发电机的配电网无功优化模型.以上文献以最小成本或最大收益为目标函数,以节点电压越限、配电变压器分接头调整能力等为约束条件建立了配电网无功优化模型,采用不同的智能算法进行模型求解,取得了不错效果.但上述文献所提出的规划模型都没有综合考虑规划方案在其使用寿命周期内的总成本以及寿命周期内降损节能收益情况,没有考虑配电网规划不同阶段的无功负荷需求.从无功规划方案长期运行角度来看,方案的初始投资、运行与维护成本对无功补偿降损节能收益具有很大影响.陈丽等[6]虽然考虑了规划方案的全寿命周期成本及降损节能收益能力,但未考虑配电网规划时预测负荷的阶段性,规划结果和实际情况会有较大偏差.因此有必要从配电网规划建设的全寿命周期角度出发,充分考虑负荷发展的需要,深入分析配电网无功补偿设备全寿命周期成本(life cycle cost,LCC)(初始投资、运行与维护成本、报废成本)及补偿后配电网降损收益能力,建立全寿命周期经济性最优的多阶段配电网无功规划模型.
计及无功补偿方案LCC及降损收益能力的多阶段配电网无功规划模型优化变量及约束条件多,模型求解极易陷入“维数灾”.本文在多粒子群算法基础[7-8]上引入混沌优化算法[9],提出了适合配电网无功规划的混沌多粒子群算法(chaos multi-swarms particle swarm optimization algorithm,CMPSO),该算法利用混沌变量的随机性、遍历性及规律性的特点,具有全局渐进收敛、易跳出局部极值点和收敛速度快的优点.利用Visual C#2005开发了配电网无功规划优化软件,实例证明了本文方法的正确性和有效性.
1 配电网无功规划数学模型
1.1 多阶段无功规划全寿命周期成本
配电网多阶段无功规划全寿命周期成本计算是以规划方案所包含的无功补偿设备全寿命周期成本为研究对象,综合考虑无功补偿设备在其整个寿命周期内发生费用的现值和,其数学模型如式(1)所示:

式中,LCC为无功规划方案全寿命周期成本现值和;N,k 分别为配电网规划的阶段数和第k 个规划阶段;u(k)为第k阶段已安装的无功补偿设备的集合;f(k)为第k阶段新装无功补偿设备的集合,在第k阶段起始安装;CI,CO,CM和CD分别为无功补偿设备的初始投资、年度运行成本、年度维护成本和报废成本(单位:万元).CIk,i为第k 阶段安装无功补偿设备i的初始投资,补偿设备初始投资包括固定成本(基本建设工程成本和控制装置成本)和动态成本(电容器成本)2部分;COk为第k 阶段无功补偿设备的年度运行损耗成本(目前无功补偿设备的有功损耗已降到0.3 W/kvar以下,故不考虑该项成本);CMk为第k 阶段无功补偿设备的年度维护成本;p(k),CDk,l分别为第k 阶段末期被拆除的补偿设备的集合和被拆除设备l 的残值(表现为收益)和设备拆除时的支出费用;PV=1/(1+r)b(k),表示第k 阶段的投资折现系数,b(k)表示第k 阶段以前无功补偿设备运行年限之和;PVsum=((1+r)g(k)-1))/(r(1+r)g(i)+m(k)),表示第k 阶段无功补偿设备年度运行维护成本现值和(等额支付现值和),g(k)表示第k阶段持续年限;r为社会贴现率.
1)第k阶段初始投资CIk
初始投资指第k阶段安装无功补偿设备所支出的费用,包括设备购置费、安装费等.在计算LCC时,除第1阶段以外,其他阶段的CIk需要折现(式(1)),CIk的计算公式如下:

式中,CIk,i为无功补偿设备i的采购、施工安装费用.
2)第k阶段年度维护成本CMk
CMk指检修人员费、设备故障检修费等,该成本贯穿设备整个寿命周期.通常供电设备维护成本取初始投资的某一比例,根据无功补偿设备的实际特点,本文维护成本取初始投资的6%.
3)第k阶段报废成本CDk
报废成本指无功补偿设备残值和报废处置费用,未到使用寿命而提前拆除的补偿设备残值还包含设备的折旧剩余价值(本文采用的是直线折旧算法).

式中,CDk,l为设备l的残值,根据配电网无功补偿设备实际数据分析,配电网无功补偿设备的平均残值约为初始投资的2%.
1.2 规划方案全寿命周期净收益现值模型
净收益现值(net present value,NPV)评价是对项目进行盈利能力分析时所采用的主要方法之一,净收益现值考虑了资金的时间价值和全部现金净流量,能较合理地反映出规划方案的收益能力.配电网无功补偿方案的NPV 是无功补偿方案全寿命周期节能收益现值减去无功补偿设备全寿命周期成本现值.多阶段配电网无功补偿方案全寿命周期净收益现值模型表示为

式中,CPk为第k 阶段安装无功补偿设备后配电网年度降损节能收益,CPk=ΔPLOSSλtmax×10-4,ΔPLOSS为实施无功补偿后配电网减少的有功损耗(通过前推回代潮流计算分别得到无功补偿前后的网损并作差得到),λ为 趸 入 电 价,tmax为 最 大 负 荷 损 耗 小 时 数;CVk为 第k 阶 段 电 压 越 界 惩 罚 费 用,Uimin))2,其中,αVk为第k 阶段电压越界惩罚因子,m(k)为第k阶段配电网节点数,
1.3 等式约束方程
等式约束方程为功率平衡方程,即
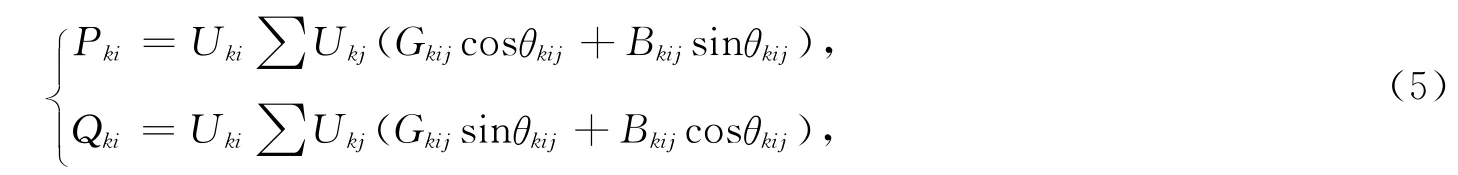
式中,Pki和Qki分别表示第k 阶段节点i的有功功率和无功功率;Uki和Ukj分别表示第k 阶段节点i和节点j的电压;Gkij和Bkij分别表示第k 阶段节点i,j之间支路的电导和电纳;θkij表示在第k 阶段节点i和j 之间电压的相角差;kj∈ki,表示在第k阶段所有与节点i相关联的节点的集合.
1.4 不等式约束方程
配电网无功规划模型中的变量还包括一部分控制变量,无功补偿电容量Q 和变压器变比T(分接头调节量)是控制变量,其不等式约束如下:

式中,Qkjmin和Qkjmax分别表示第k阶段补偿点补偿容量下限和上限,nku为第k 阶段补偿点数;Tkgmin和Tkgmax分别表示第k阶段变压器变比下限和上限,nkt为第k 阶段变压器台数.
2 适用于配电网无功规划的改进粒子群算法
以无功补偿方案全寿命周期净收益现值最大为目标函数的多阶段无功规划模型优化变量多(2阶段无功规划粒子维数是单阶段无功规划粒子维数的2倍),对求解算法的寻优能力提出了更高要求,本文在多种群粒子群算法的基础上,提出了一种改进粒子群算法.
2.1 改进算法基本原理
改进粒子群算法(CMPSO)的基本进化方程为

式中,下标i表示第i个粒子,d 表示粒子维数,即无功补偿的节点数,xid表示节点d 的无功补偿容量;c1,c2,c3为学习因子,r1,r2,r3为区间[0,1]内的随机数;Pi,Pg,Zg分别为粒子i,子种群中粒子和所有种群中粒子的历史最优解.
常规粒子群算法种群内部粒子具有“趋同性”,在解决配电网无功规划优化问题时,通常迭代到20~30代左右时,所有粒子都开始收敛到当前最优解附近,即c1,c2都接近于0.多种群粒子群协同优化算法在寻优过程中,各子种群的粒子会受到种群最优粒子Zg的影响,早熟现象能得到一定程度的改善,但仍然存在明显的“早熟”问题.为了抑制算法早熟、增强算法全局搜索能力,本文将随机Logistic混沌映射序列融入到粒子运动过程,利用混沌运动的随机性、遍历性及规律性的特点,使局部最优粒子迅速逃离局部极值点,避免早熟,提高算法的寻优能力,具体优化过程如下:
1)用式(8)将新粒子xi(t+1)与其所在子种群空间中的其他粒子xj进行相似度比较,相似度高的粒子转2)进行混沌优化.

式中,D 为粒子维数,δ为常数,本文取0.1.
2)首先利用公式(9)将粒子xj(t)映射到区间[0,1],产生混沌变量序列(t);然后代入Logistic方程——公式(10)进行混沌映射,由于实际配电网中进行无功补偿的节点数远小于配电网的总节点数,即xjd=0的概率较高,当xjd=0带入Logistic方程后,混沌效应消失,粒子变异能力减弱.为了提高粒子的多样性,本文对常规混沌映射进行了改进,当xjd=0时,利用公式(11)对输入量进行随机变异混沌映射,公式(11)中α取0.15(通过无功规划优化实例验证,α取0.15时算法全局寻优能力较好),最后利用公式(12)将新混沌序列还原到原来的解空间.

式中,R 为无功补偿设备最大约束容量.

式中,μ 为控制参量,取4.

式中,m=random()为[0,1]上的随机数,随机因子α为小于1的常数.

2.2 基于CMPSO 算法的配电网无功规划优化
基于上述模型和算法的配电网多阶段无功规划优化程序流程如图1.

图1 基于CMPSO 算法的配电网多阶段无功规划优化程序流程Fig.1 Program flow of the multi-stage reactive power planning of distribution network based on CMPSO
3 实例验证

图2 2阶段配电网网架结构Fig.2 Two-stage power distribution network structure
为了验证多阶段无功规划方法的优点,本文将上述无功规划方法应用于文献[11]中的10kV配电网,分别进行了单阶段和多阶段无功规划优化及其规划结果对比分析.配电网初始网架如图2所示,其中实线表示已有网架,粗虚线表示5年规划,细虚线(支路8、9)表示10年规划,节点1为电源节点(平衡节点),其他9个节点为负荷点(PQ 节点),其中节点3,5,6,7,9为第1阶段规划水平年负荷(取第5 年负荷水平),节点8,10为第2阶段规划水平年负荷(取第10年负荷水平).
各支路详细参数和负荷分别如表1和表2所示,其他数据如下:趸入电价0.5元/kWh,最大负荷损耗5 000h,寿命周期取10年,社会折现率取0.04,每点自动投切无功补偿装置固定投资8 000元,电容器价格50元/kvar(补偿容量为10的整数倍),各节点补偿容量0~1 200kvar.
3.1 单阶段无功规划
单阶段无功规划在10年规划周期内采用一种无功补偿方案,根据是否考虑负荷发展的阶段性,建立以单一负荷水平(第10年负荷水平,传统无功优化通常采用该种负荷模型)时全寿命周期净收益现值最大为目标函数的规划模型和同时满足2阶段负荷水平(第5年和第10年负荷水平)时单阶段全寿命周期净收益现值最大化为目标函数的规划模型,利用本文提出的CMPSO 算法对上述模型进行求解,规划结果分别如表3方案1和方案2所示.
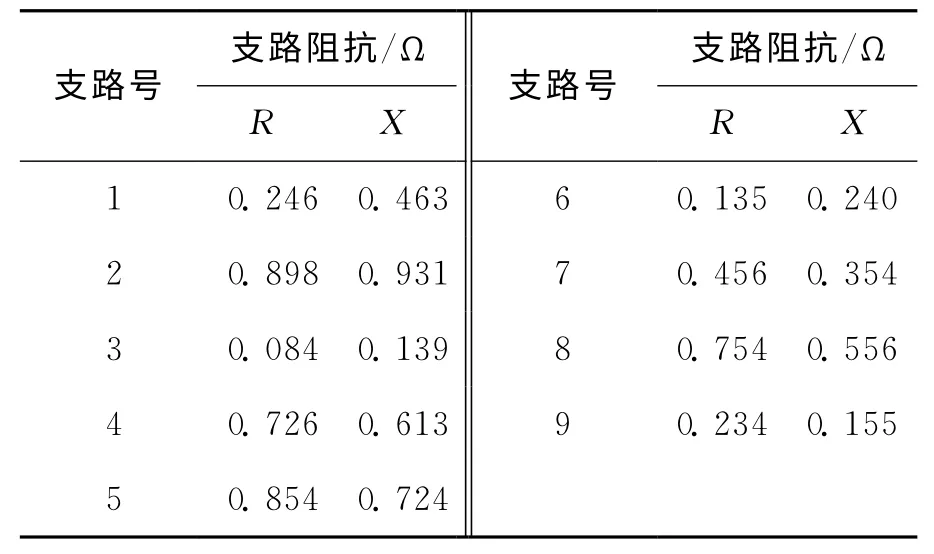
表1 馈线阻抗参数Tab.1 Impedance of feeders
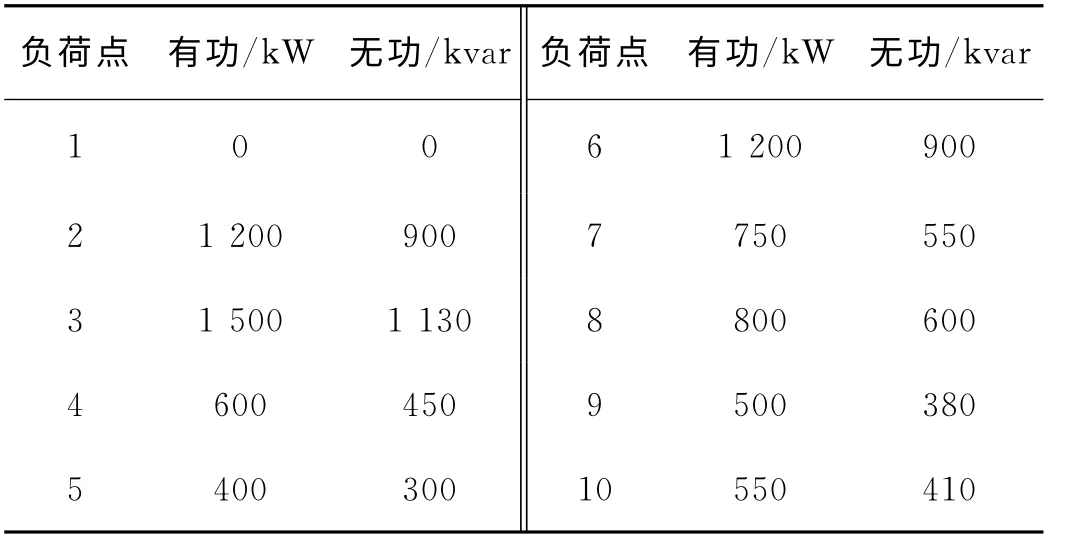
表2 负荷参数Tab.2 Parameter of loads
3.2 多阶段无功规划
多阶段无功规划把规划分2阶段进行,第1阶段从第1年到第5年,第2阶段为第6年到第10年.多阶段无功规划的2阶段可能采用不同的无功补偿方案,因此多阶段无功补偿方案包括2个子方案,即第1阶段无功补偿方案和第2阶段无功补偿方案,多阶段无功规划是以2阶段补偿方案净收益现值总和最大为目标函数.利用本文提出的混沌多粒子群算法对上述模型进行求解,规划结果如表4所示.

表3 单阶段规划结果Tab.3 Single stage planning results

表4 多阶段规划结果Tab.4 Multi-stage planning results
不同规划方案的全寿命周期成本构成如表5所示.方案3的报废成本比较大,因为方案3在第2阶段新增补偿点8,在第2阶段末时,节点8的无功补偿设备只使用了5年,还具有较多残值,而其他设备残值只有初始投资的2%,残值表现为收益,所以前面加负号.以上3种规划方案实施前后配电网网损变化情况如表6所示.

表5 各方案成本构成Tab.5 Cost comparison of all schemes 万元

表6 无功补偿前后网损对比Tab.6 Loss comparing before and after the reactive power compensation /kW
3.3 无功规划结果分析
1)从表5的LCC统计和降损节能收益数据可以看出,补偿方案全寿命周期成本相对于补偿方案的全寿命周期降损节能收益是十分可观的投入,在确定补偿方案时需要认真考虑补偿方案全寿命周期成本.
2)从实施无功补偿后系统网损的减少程度来看,在第1阶段方案2降损效果最好(网损从57.70kW 减少到40.68kW),在第2阶段方案1降损效果最好(网损从82.26kW 减少到57.57kW),但净收益现值最大的规划方案却是方案3为25.042万元.方案1全寿命净收益现值比较小的原因是,方案1优化目标函数的负荷水平都按最大负荷补偿,所以尽管补偿后系统网损降低的较多,但补偿方案的初始投资和运行维护成本更高,设备等效利用率低,所以收益不理想;方案2虽然考虑了2阶段的负荷水平,但用1种补偿方案兼顾2阶段的负荷水平,不能实现2阶段都是最优补偿.只有方案3以2阶段、2种补偿方案最优为目标函数,因此能得到最优的全寿命净收益现值.但是2阶段最优无功补偿目标函数是第1阶段最优补偿目标函数和第2阶段最优补偿目标函数之和最优,优化变量为单阶段优化变量的2 倍,所以对优化算法提出了更高的要求.
3.4 改进粒子群算法性能分析
由于多阶段配电网无功规划模型优化变量多,应用智能优化算法进行求解时,各次结果可能不同.为了验证本文提出的CMPSO 算法的寻优性能,分别用CMPSO 算法、MPSO(多粒子群协同优化算法)和基本PSO(粒子群算法),对本文提出的单阶段和2阶段无功规划算例进行50次求解,用平均迭代次数和找到最优解次数这2个参数来比较3种算法的寻优能力,结果对比如表7所示.
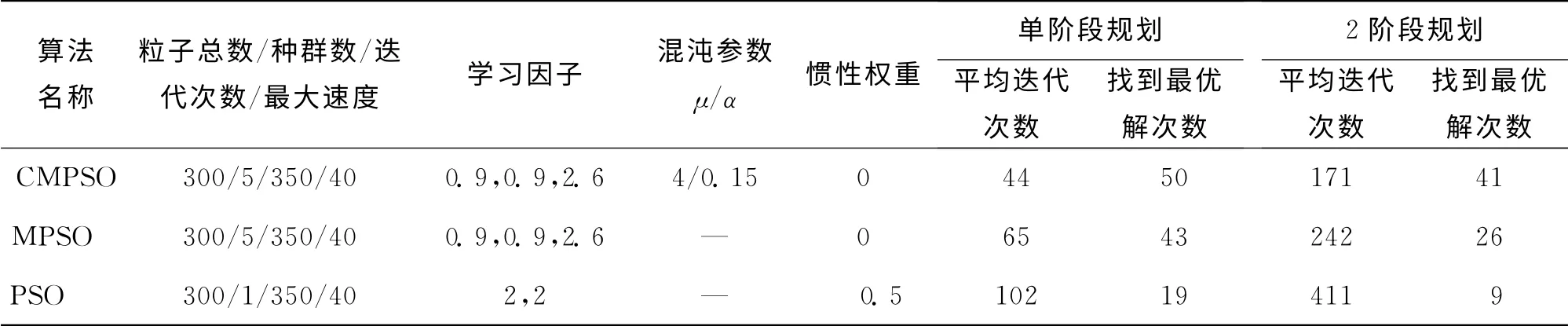
表7 算法寻优能力比较Tab.7 Comparison of three algorithms in optimization
由表7结果可知,CMPSO 算法收敛速度快、全局寻优能力最强、寻优结果稳定性高.
4 结论
根据配电网多阶段无功规划的特点,基于全寿命周期成本管理理论,建立了以全寿命周期净收益现值最大为目标函数的多阶段配电网无功规划模型,通过实例分析得出如下结论:
1)多阶段配电网无功规划不是单阶段无功规划的简单叠加,考虑了配电网各个阶段无功负荷需求的变化,从总体经济最优的角度决定配电网全寿命周期内无功补偿设备的建设时间及安装容量,实现全寿命周期经济效益最大化.
2)计及无功补偿方案的LCC,以补偿方案降损节能收益最大为目标函数的配电网无功规划模型能更好地折中补偿方案投资成本和降损节能收益,得到全寿命周期经济效益最好的补偿方案.
3)针对配电网多阶段无功优化问题,提出了随机混沌多粒子群算法,在不过多增加计算量的同时,显著提高了算法的寻优能力.
[1] 苏海锋,张建华,梁志瑞,等.基于LCC 和改进粒子群算法的配电网多阶段网架规划优化[J].中国电机工程学报,2013,33(4):118-125.SU Haifeng,ZHANG Jianhua,LIANG Zhirui,et al.Power distribution network multi-stage planning optimization based on LCC and improved PSO[J].Proceeding of the CSEE,2013,33(4):118-125.
[2] 胡泽春,钟明明,王佳贤,等.考虑多负荷水平的中低压配电网无功补偿优化规划[J].电工技术学报,2010,25(8):167-173.HU Zechun,ZHONG Mingming,WANG Jiaxian,et al.Optimal reactive power compensation for medium and low voltage distribution network considering multiple load levels[J].Transactions of China Electrotechnical Society,2010,25(8):167-173.
[3] 杨丽徙,丁荣刚,王西训.工业企业配电网无功电源的两阶段优化规划[J].电力系统及其自动化学报,2010,22(2):32-36.YANG Lixi,DING Ronggang,WANG Xixun.Two-phase optimization planning of reactive power supply for factory power grid[J].Proceedings of the CSU-EPS,2010,22(2):32-36.
[4] 汪超,王昕,姚钢,等.基于黄金分割的混沌粒子群优化算法在配电网无功规划中的应用[J].电力系统保护与控制,2012,40(7):31-36.WANG Chao,WANG Xin,YAO Gang,et al.Application of golden section based chaos particle swarm optimization algorithm in distribution network reactive power optimization[J].Power System Protection and Control,2012,40(7):31-36.
[5] 朱勇,杨京燕,高领军,等.含异步风力发电机的配电网无功优化规划研究[J].电力系统保护与控制,2012,40(5):80-85.ZHU Yong,YANG Jingyan,GAO Lingjun,et al.Research on optimal reactive power planning for distribution network containing asynchronous wind power generators[J].Power System Protection and Control,2012,40(5):80-85.
[6] 陈丽,苏海锋,张晋国.基于改进共享小生境遗传算法的配电网无功规划[J].河北大学学报:自然科学版,2011,31(3):314-318.CHEN Li,SU Haifeng,ZHANG Jinguo.Research on reactive power planning of distribution network based on the sharing niche genetic algorithm[J].Journal of Hebei University:Natural Science Edition,2011,31(3):314-318.
[7] 黄席樾,向长城,殷礼胜.现代智能算法理论及应用[M].北京:科学出版社,2009:224-228.
[8] 许珂,刘栋.多粒子群协同进化算法[J].计算机工程与应用,2009,45(3):51-54.XU Ke,LIU Dong.Algorithm of multi-PSO co-evolution based on GA and PSO[J].Computer Engineering and Applications,2009,45(3):51-54.
[9] 胥小波,郑康锋,李丹,等.新的混沌粒子群优化算法[J].通信学报,2012,33(1):24-31.XU Xiaobo,ZHANG Kangfeng,LI Dan,et al.New chaos-particle swarm optimization algorithm[J].Journal on Communications,2012,33(1):24-31.
[10] 刘小华,刘沛,张步涵,等.逐级均值聚类算法的RBFN 模型在负荷预测中的应用[J].中国电机工程学报,2004,24(2):17-21.LIU Xiaohua,LIU Pei,ZHANG Buhan,et al.Application of RBFN model for load forcasting based on ranking means clustering[J].Proceedings of the CSEE,2004,24(2):17-21.
[11] 康庆平,周雷.一个实用的配电网优化规划方法[J].电网技术,1994,18(6):39-43.KANG Qingping,ZHOU Lei.An efficient method of optimum planning for distribution systems[J].Power System Technology,1994,18(6):39-43.
