基于模糊几何加权的区间多目标规划问题
2015-07-24郭子雪郑玉蒙李双双
郭子雪,郑玉蒙,李双双
(河北大学 管理学院,河北 保定 071002)
在许多实际决策问题中,由于人们认知的局限性以及问题的复杂性,只能获取某不确定参数的变动范围,此时可以采用区间数的形式来表达不确定信息,因此对区间多目标规划问题的研究具有显著的现实意义.目前,对于区间多目标规划问题的求解方法,大部分是将不确定的问题转化为确定的问题[1],再把多目标规划问题转化为单目标规划问题.乔辰等[2]提出了多目标规划问题的几何加权法,陈朋永等[3]运用模糊几何加权法研究了电力系统经济调度问题,二者均是将多目标规划问题转化为单目标规划问题;杨亭亭[4]提出了4种求解区间线性规划问题的方法,其中BWC方法就是把区间线性规划问题分为最好最优值模型和最差最优值模型;针对区间多目标规划问题的求解方法,郭均鹏[5-6]等人提出:先将区间多目标规划转化为含参数的确定的多目标规划[7],再转化为单目标的区间规划问题,通过求解该单目标的区间规划问题[8],得到原区间多目标规划问题的最优值区间;夏昊冉[9]针对区间多目标规划问题,提出了几种智能优化算法,打破了传统算法对函数性质的苛刻要求,解决了一系列非线性、非连续性问题;徐秀梅等[10]针对含有区间数的证券投资组合问题,考虑到目标函数的重要性不同,提出了线性加权和法.
基于区间多目标规划问题中目标函数的重要性不同,本文提出了改进的模糊几何加权法.该方法不仅考虑了区间多目标规划问题的模糊性,而且考虑了各个目标函数权重的大小,并通过求解转化的单目标规划模型,得到原区间多目标规划模型的非劣解以及最优值区间.
1 区间多目标规划问题
1.1 基本概念
考虑如下形式的区间多目标规划问题:
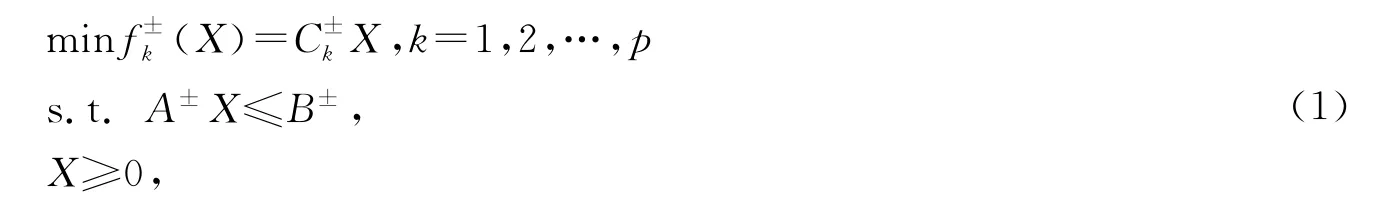
式中X=(x1,x2,…,xn)T为自变量向量;系数k=1,2,…,p;A±为系数矩阵,每个元素为相互独立的区间数,且j=1,2,…,n,其中,依此类推B±为约束条件的右端向量,且
定义1[11]对于上述区间多目标规划问题,任意取…,m,j=1,2,…,n.由原区间多目标规划问题可以得到确定型的多目标规划问题,称该确定型多目标规划问题的一个有效解为原区间多目标规划问题的一个有效解或非劣解,且该确定型多目标规划问题的一个最优解为原区间多目标规划问题的一个最优解.
1.2 区间多目标规划问题的确定型转化
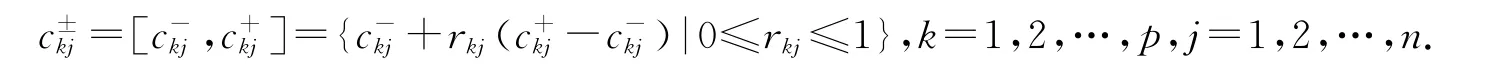
同理,对系数矩阵A±中的元素和右端向量B±中的元素做类似处理,有
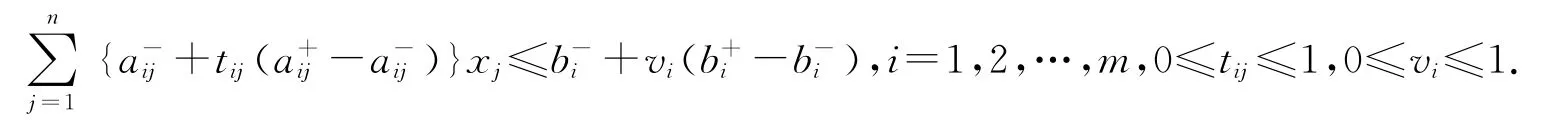
令rkjxj=skj,qij=tijxj,则

其中,S=(sk1,sk2,…,skn)T,k=1,2,…,p,i=1,2,…,m.
由此得到如下含参数的确定的多目标规划问题:
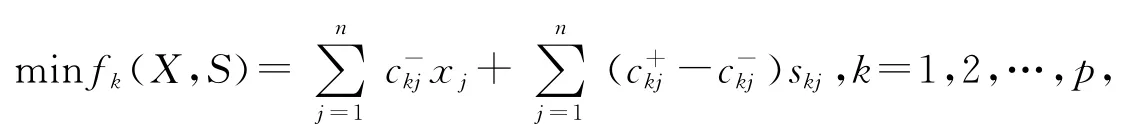
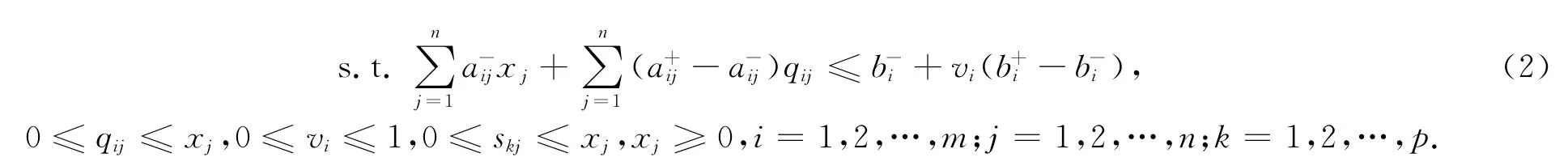
2 模糊几何加权法求解区间多目标规划问题
2.1 模糊几何加权法
模糊几何加权法求解多目标规划问题,考虑到了各个目标函数的不同重要性,通过把目标函数的隶属函数进行几何加权来把多目标规划问题转化为单目标规划问题.因此通过对模型(2)中各个目标函数的隶属函数进行几何加权,得到如下模型:
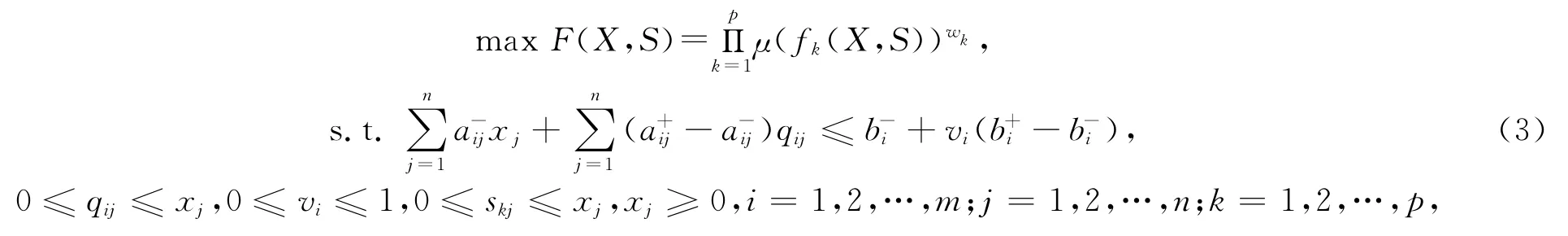
其中,wk表示各个目标函数的权重,并且表示各目标函数的隶属函数.为了求解目标函数的隶属函数μ(fk(X,S)),首先求解如下单目标线性规划问题(4)和(5):
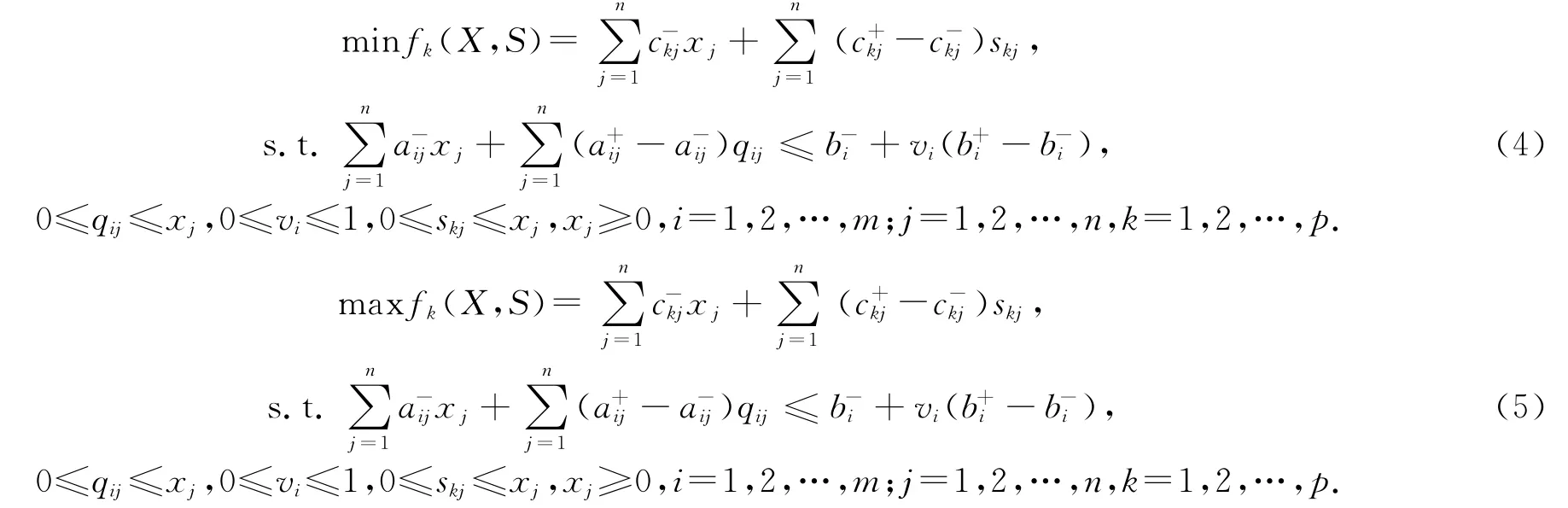
设模型(4)和(5)的最优值分别为fk,min和fk,max,可取目标函数的隶属函数为
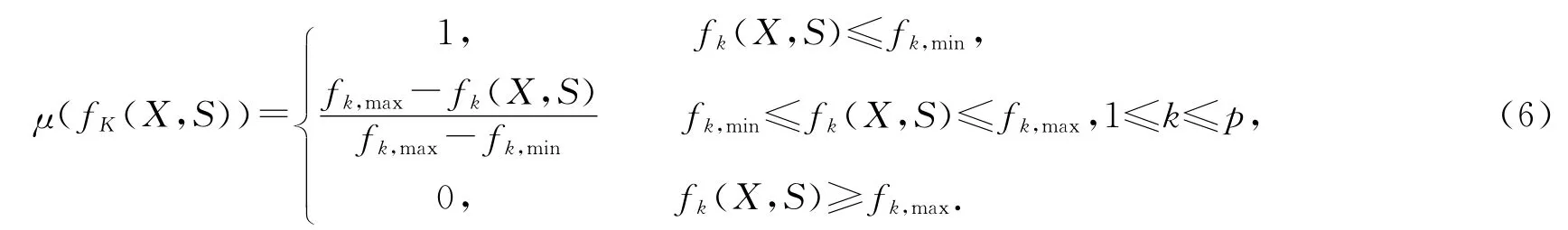
利用最大最小算子法[12-13],结合式(6)可以得到模型(3)的等价模型(7):
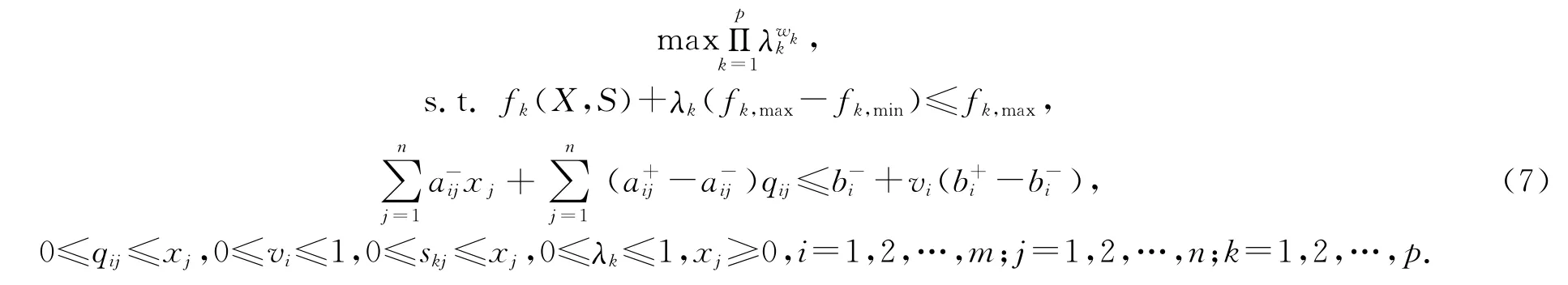
定理1 设模型(7)的最优解为X*,则X*为模型(2)的有效解或非劣解.
证明:采用反证法.假设X*不是模型(2)的非劣解,那么必定存在一个改进的可行解X**,使得μ(fk(X*,S*))≤μ(fk(X**,S**)),即λk(X*,S*)≤λk(X**,S**).设当wk的值一定时,M 为关于λk(X,S)的单调增函数,因此M(λk(X*,S*))≤M(λk(X**,S**)).又由题设知,X*为模型(7)的最优解,而现在又找到一个X**,使得M(λk(X**,S**))的值比M(λk(X*,S*))的值好,这与题设相矛盾,因此可得X*为模型(2)的有效解或非劣解.
模型(7)为含参数的单目标规划问题,可以通过求解其最优模型和最差模型得到原区间多目标规划问题的最优值区间.
定理2 模型(7)的最优模型为

类似证明,可得定理3.
定理3 模型(7)的最差模型为
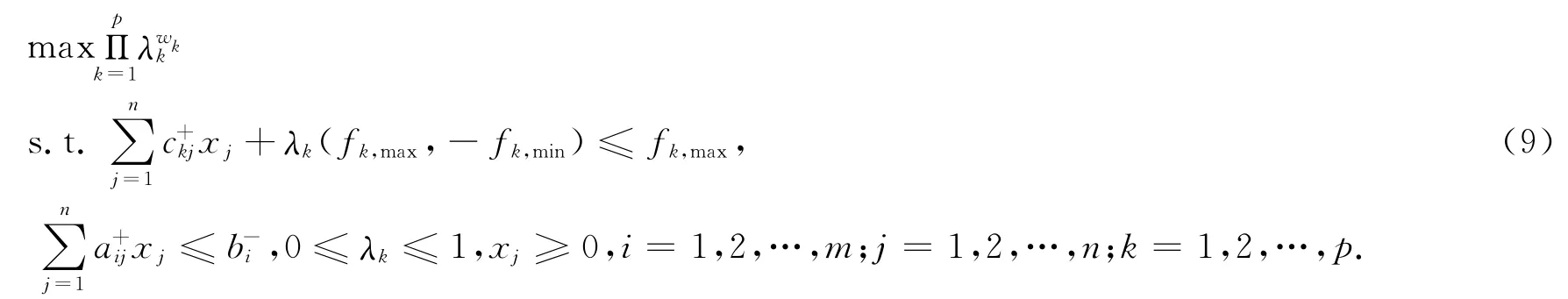
可以证明:由模型(8)、模型(9)解得的λ+和λ-,分别代表模型(1)中当目标函数分别取不同权重时的最大总满意度和最小总满意度,可得满意度区间[λ-,λ+].将由模型(8)求得的最优解代入原区间多目标规划问题(1)的最优目标函数,得到最优目标函数值f-k;将由模型(9)求得的最优解代入原区间多目标规划问题(1)的最差目标函数,得到目标函数值f+k.由此可得,当目标函数分别取不同的权重时原区间多目标规划问题的最优值区间,其中k=1,2,…,p.
2.2 模糊几何加权法求解区间多目标规划问题的步骤
Step1利用区间数的排序函数以及变量替换的方法把原区间多目标规划问题转化成为含参数的确定型的多目标线性规划问题.
Step2 根据各个目标函数的重要性的不同,给定各个目标函数不同的权重wk,然后对每个目标函数的隶属函数进行几何加权构造单目标规划模型(3).
Step3 确定模型(3)中各个目标函数的隶属函数μ(fK(X,S)).
Step4 结合最大最小算子法,得到单目标规划模型(3)的等价模型(7).
Step5 通过求解单目标规划模型(7)的最优模型和最差模型,得到当原区间多目标规划问题的目标函数分别取不同的权重时的非劣解以及最优值区间[f-k,f+k].
3 算例分析
设某应急系统有3个应急需求点D1,D2,D3,5个应急物资供应点S1,S2,S3,S4,S5.各应急需求点的需求量、应急物资供应点的供应量以及从各应急物资供应点到各需求点调运应急物资的运输时间和单位运输成本等数据如表1所示.已知各需求点的目标应急调运时间(单位:h)限制期为:T01=4,T02=5,T03=5;各应急物资供应点的启用成本(单位:万元)分别为c1=[130,140],c2=[120,140]c3=[170,200],c4=[100,120],c5=[180,200].试确定应急物资调运方案使应急物资调运的时间和总费用达到最小.相关数据见表1.
设xij表示从应急物资供应点Si运往应急物资到应急需求点Dj的应急物资数量(i=1,2,3,4,5;j=1,2,3);yij为0~1决策变量,当应急物资供应点Si为应急需求点Dj提供应急物资时yij取1,否则yij取0;yi为0~1决策变量,当启用应急物资供应点Si时yi取1,否则yi取0.则上述问题的区间数模糊规划模型为
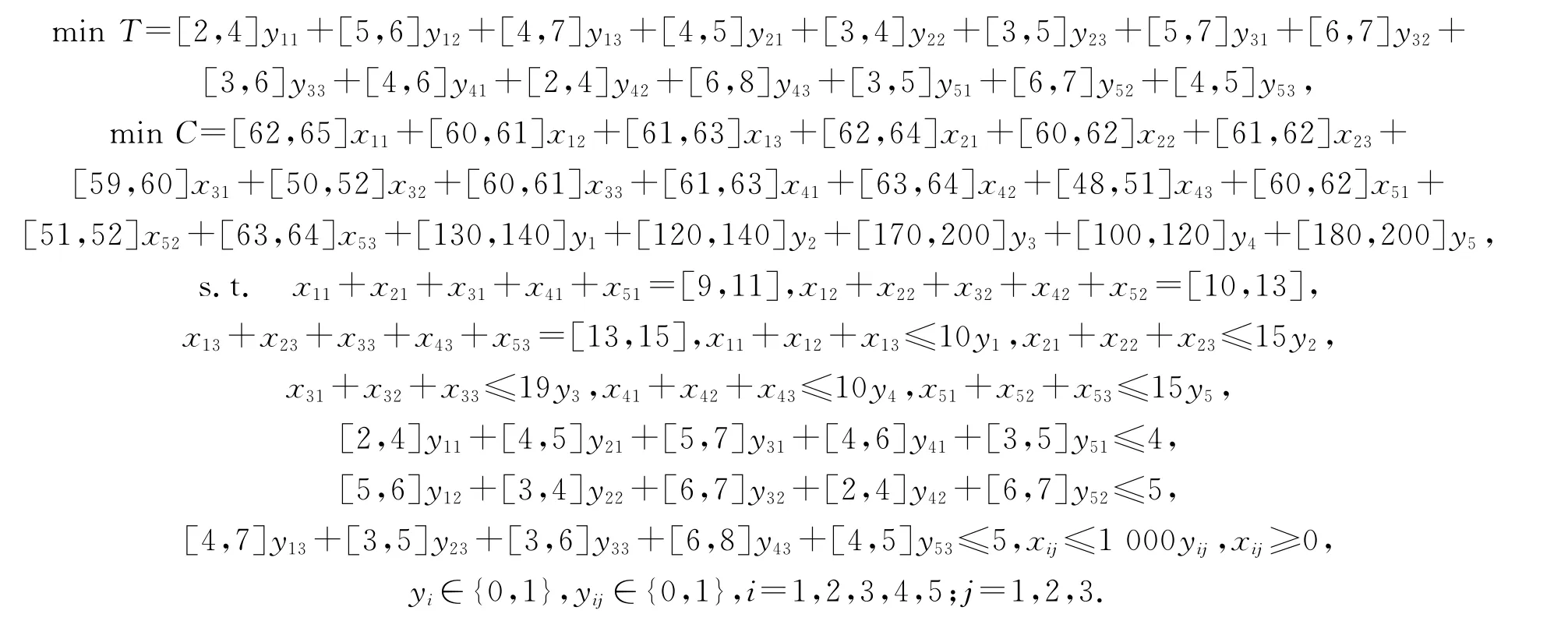

表1 应急物资运输时间和单位运输成本等相关数据Tab.1 Emergency supplies transportation time and the unit transportation cost and other relevant data
将上述模型转化为含参数的确定型多目标规划问题,分别求解各单目标规划可得:
Tmin=7,Tmax=14,Cmin=2 292,Cmax=3 290.
取w1=0.6,w2=0.4,代入模型(8)和(9),解之可得总满意度区间和目标函数最优值区间如表2所示:

表2 模糊几何加权法的求解结果Tab.2 Results of fuzzy geometric weighting method
其中,最小总满意度下和最大总满意度下的非劣解均为
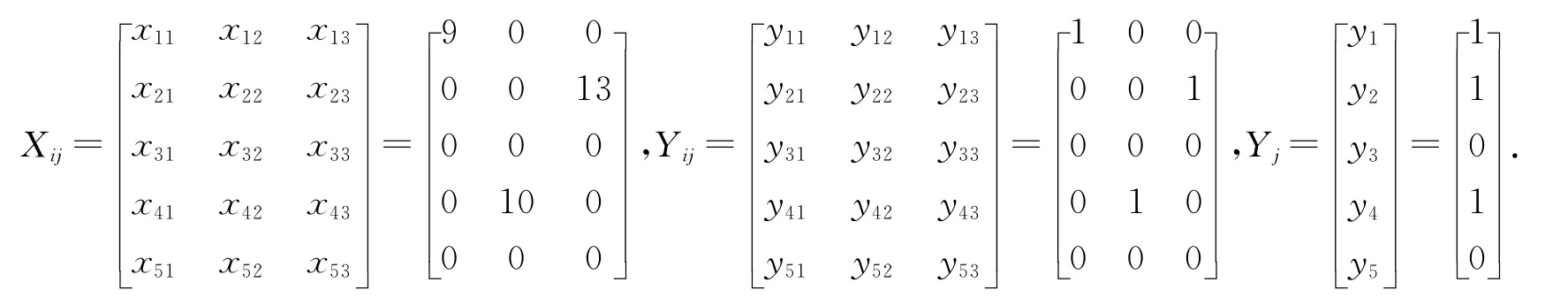
4 结论
区间多目标规划问题是实际决策问题中常见的一种形式,研究区间多目标规划问题的求解方法具有重要的现实意义和理论价值.考虑到区间多目标规划问题中各目标函数重要性的不同,本文提出了一种改进的模糊几何加权法,该方法通过定义目标函数的隶属度函数,构建了与区间多目标规划问题等价的模糊几何加权单目标规划模型,从而将区间多目标规划问题转化为单目标的区间规划问题.最后的算例分析验证了该方法的可行性和有效性.
[1] 韩世莲.区间数多目标多模式运输问题的模糊规划方法[J].系统工程理论方法应用,2006,15(5):452-455.HAN Shilian.Fuzzy programming approach for multi-objective solid transportation problem with interval parameters[J].Systems Engineering-Theory Methodology Applications,2006,15(5):452-455.
[2] 乔辰,张国立.几何加权法求解多目标规划问题[J].华北电力大学学报,2011,38(6):108-111.QIAO Chen,ZHANG Guoli.Geometric weiheting method for solving multi-objective programming problems[J].Journal of North China Electric Power University.,2011,38(6):108-111.
[3] 陈朋永,赵书涛,乔辰,等.模糊几何加权法求解电力系统经济调度问题[J].电力科学与工程,2012,28(5):1-5.CHEN Pengyong,ZHAO Shutao,QIAO Chen,et al.Fuzzy geometric weighting method of solving economic dispatch in power system[J].Electric Power Science and Engineering,2012,28(5):1-5.
[4] 杨亭亭.区间多目标规划在区域水资源优化调度中的应用[D].北京:中国石油大学,2011.YANG Tingting.The application of interval multi-objective programming in regional water resources optimal allocation[D].Beijing:China University of Petroleum,2011.
[5] 郭均鹏,李汶华.区间多目标线性规划的模糊求解方法[J].系统管理学报,2008,17(4):462-466.GUO Junpeng,LI Wenhua.Fuzzy method to solve interval multi-objective linear programming[J].Journal of Systems &Management,2008,17(4):462-466.
[6] 王冲,邱志平.区间多目标线性优化的功效系数求解方法[J].北京航空航天大学学报,2013,39(7):908-916.WANG Chong,QIU Zhiping.Efficiency coefficient method to solve interval multi-objective liner optimization problems[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):908-916.
[7] ZIMMERMANN H J.Fuzzy programming and linear programming with several objective functions[J].Fuzzy Sets and Systems,1978,1(1):44-45.
[8] 宋业新,姜礼平,陈绵云.一类模糊线性规划模型的模糊最优区间值[J].模糊系统与数学,2002,16(2):86-91.SONG Yexin,JIANG Liping,CHEN Mianyun.Fuzzy optimal interval value for a fuzzy linear programming model[J].Fuzzy Systems and Mathematics,2002,16(2):86-91.
[9] 夏昊冉.区间系数多目标规划的智能优化算法[D].合肥:安徽大学,2011.XIA Haoran.The intelligent optimization algorithm of multi-objective programming with interval coefficient[D].Hefei:Anhui University,2011.
[10] 徐秀梅,孙玉华.基于区间数的多目标证券投资组合问题[J].济南大学学报,2014,28(3):216-219.XU Xiumei,SUN Yuhua.Multi-objective portfolio selection based on interval number[J].Journal of University of Jinan,2014,28(3):216-219.
[11] 郭均鹏,李汶华.区间线性规划的标准型及其最优值区间[J].管理科学学报,2004,7(3):60-63.GUO Junpeng,LI Wenhua.Standard form of interval linear programming and its optimal objective interval value[J].Journal of Management Sciences in China,2004,7(3):60-63.
[12] TONG S.Interval number and fuzzy number linear programming[J].Fuzzy Sets and Systems,1994,66:301-306.
[13] BELLMANR E,ZADEH L A.Decision making in a fuzzy environment[J].Management Science,1970,17:141-164.
[14] 张吉军.区间数线性规划问题的最优解[J].系统工程与电子技术,2001,23(9):53-55.ZHANG Jijun.The optimal solution of interval number linear programming problem[J].Systems Engineering and Electronics,2001,23(9):53-55.
[15] 郭子雪,王兰英,齐美然,等.基于区间数信息的区域应急物资储备库选址多目标决策模型[J].灾害学,2015,30(2):148-151.GUO Zixue,WANG Lanying,QI Meiran,et al.A fuzzy multi-objective decision making approach of emergency material storage location based on interval number[J].Journal of Catastrophology,2015,30(2):148-151.
