非线性奇异系统边值问题解的平方收敛性
2015-07-24王培光刘向
王培光,刘向
(1.河北大学 电子信息工程学院,河北 保定 071002;2.河北大学 数学与信息科学学院,河北 保定 071002)
在实际应用领域有许多利用奇异系统描述的数学模型,例如最优控制、电路、人口增长模型等等,奇异系统是一类较微分系统更为复杂的系统[1-3].其中解的收敛性问题是人们关注的问题之一,其对奇异微分系统定性理论的发展有着重要的影响.拟线性化方法是构造非线性问题近似解的一种非常有效的方法.Bellman等[4]首次提出了这种源于动态规划理论的方法.Lakshmikantham 等[5]系统地总结了拟线性化方法在常微分方程中的应用结果.之后相继出现各种动力系统的推广结果[6-10].然而,拟线性化方法在奇异系统中的应用结果很少[11-13],特别是对于带有边界条件的奇异非线性系统解的收敛性未见研究结果.
本文应用拟线性化方法研究具有边界条件的非线性奇异微分系统解的收敛性问题,主要工作包括构造非线性奇异系统的单调序列,并通过拟线性化方法证明该问题解的一致和平方收敛性结果.
1 预备知识
考虑下列奇异非线性系统边值问题(BVP)

这里A 是奇异n×n矩阵,E,F 是非奇异n×n实矩阵,x∈Rn,f∈C(J×Rn,Rn),J=[0,c],c是正常数.
定义1 称函数α0∈C1(J,Rn)为边值问题(1)的下解,如果下列不等式成立

定义2 称函数β0∈C1(J,Rn)为边值问题(1)的上解,如果下列不等式成立

给出集合: S(α0,β0)={u∈C(J,Rn):α0(t)≤u(t)≤β0(t),t∈J},
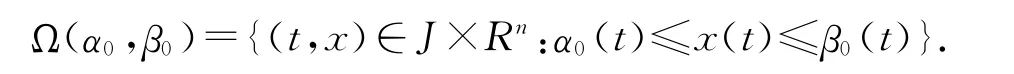
在进一步的讨论中,将会用到线性奇异微分系统的相关结果.首先考虑奇异微分不等式

其中A,M(t)是n×n矩阵,A 是奇异矩阵,M(t)是连续矩阵,t∈J,E-1,F-1≥0.
引理1 假设
H1)存在常数λ∈R 使得,L(t)=[λA+M(t)]-1≥0存在并且=AL(t)是常数矩阵;
H2)存在非奇异矩阵T 使得T-1,(LT)-1存在,并且T-1,(LT),(LT)-1≥0,满足
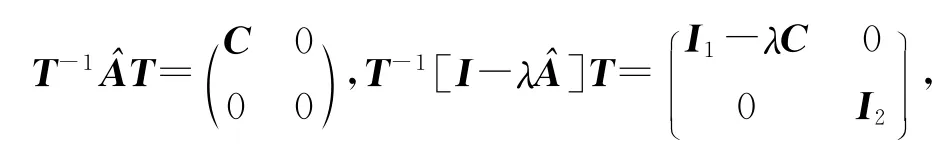
其中C 是对角阵,C-1≥0,则Ex(0)≤0,Fx(c)≤0蕴含x(t)≤0,t∈J.
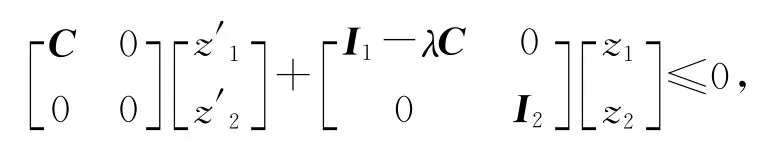
由此得出Cz′1+(I1-λC)z1≤0且z2≤0.由于E-1,(LT)-1非负,则由Ex(0)=ELTz(0)≤0可得z(0)≤0.
同样的,可得z(c)≤0.由于C-1≥0,则由Cz′1+(I1-λC)z1≤0解得
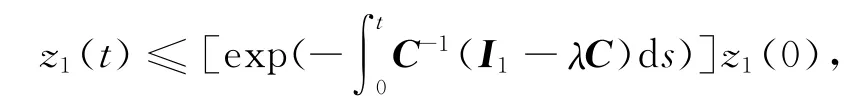
从而,z1(t)≤0.因此,z(t)≤0,t∈J.综上可知,LTz(t)≤0或x(t)≤0,t∈J.
对于边值问题(1),证明如下的比较结果.
引理2 假设条件H1)—H2)成立并且满足
H3)函数α0,β0∈C1(J,Rn)是边值问题(1)的下解和上解,fx(t,x)存在并且连续,则α0(t)≤β0(t),t∈J.
证明:由条件H3)得取M(t)=则有A(α0-β0)′+M(t)(α0-β0)≤0,又因为E(α0(0)-β0(0))≤0,F(α0(c)-β0(c))≤0,利用引理1,可知α0(t)≤β0(t),t∈J.
对于奇异线性边值问题
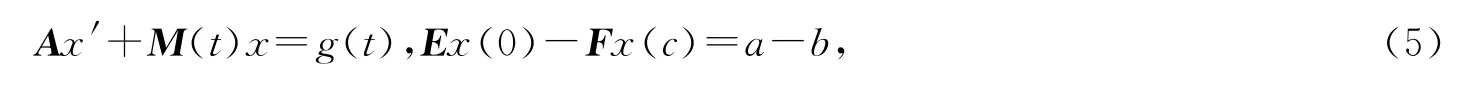
有如下结果:
引理3[14]假设引理1的条件H1)成立,index(A)=1,
H4)边界条件满足Q=E-Fexp(-ÂDM^c)可逆,则边值问题(5)的唯一解可表示为

其中
2 主要结果
定理1 假设下列条件成立:
A1)函数α0,β0∈C1(J,Rn)分别是边值问题(1)的下解和上解.
A2)偏导数fx(t,x)在Ω(α0,β0)上存在且连续,并且关于x 拟单调非减,|fx(t,x)-fx(t,y)|≤L|x-y|,x,y∈S(α0,β0),L>0,其中L 为n×n矩阵.
A3)条件H1)-H4)成立,则存在单调序理{αn},{βn}一致且平方收敛于边值问题(1)的解.
证明:由条件A1)-A3)可知引理2 的条件成立.因此,对于边值问题(1)的上解和下解,有α0(t)≤β0(t),并且由假设A2),有
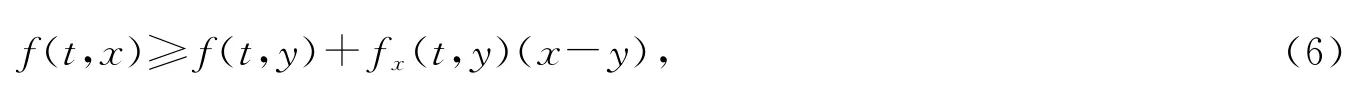
其中α0(t)≤y≤x≤β0(t),t∈J.
设αn+1,βn+1分别为奇异微分系统(7)、(8)的解.
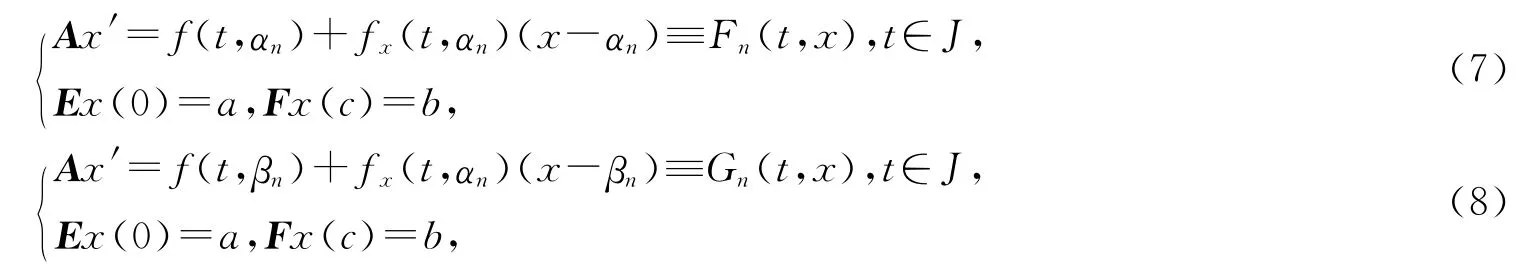
容易证明,BVP(7)有唯一解.设x1,x2为BVP(7)的2 个解,并且注意到E(x1(0)-x2(0))=0,F(x1(c)-x2(c))=0,则由BVP(7),得
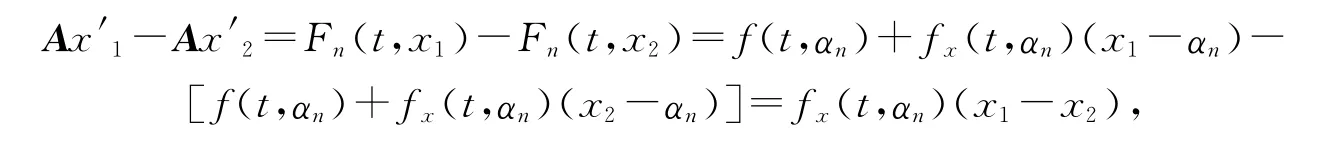
显然上式的解是奇异线性系统A(x1-x2)′-fx(t,αn)(x1-x2)=0,Ex1(0)-x2(0))-F(x1(c)-x2(c))=0的解.因此,由引理3,利用x(t)的表达式得x1=x2,从而得出BVP(7)有唯一解.类似的,可以证明BVP(8)有唯一解.
下面证明α0≤α1≤β1≤β0,t∈J.设p=α0-α1,有Ep(0)≤0,Fp(c)≤0.由条件(A1)和BVP(7),可得
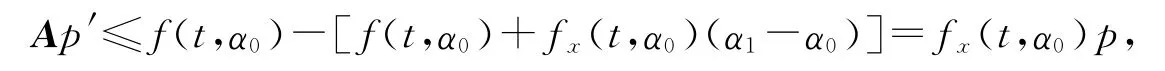
其中M(t)=-fx(t,η(t)),α0(t)≤η(t)≤β0(t),t∈J.因此,由引理1,得p(t)≤0,即α0(t)≤α1(t),t∈J.类似的,设p=β1-β0,在t∈J 上有β1(t)≤β0(t)成立.
下面证明α1(t)≤β1(t),t∈J.由于α(t)≤α(t),利用不等式(6)和BVP(7),可得
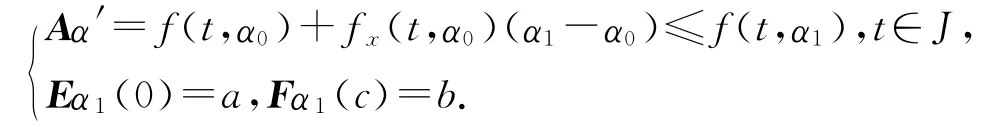
同样的,由条件A2)和BVP(8),可知

从而得出α1和β1 分别为BVP(1)的下解和上解.由引理2得α1(t)≤β1(t),t∈J.因此,得α0(t)≤α1(t)≤β1(t)≤β0(t),t∈J.由归纳法,得到单调序列{αn(t)},{βn(t)}满足
α0(t)≤α1(t)≤…≤αn(t)≤βn(t)≤…≤β1(t)≤β0(t),t∈J.
设x为BVP(1)的任意解且满足α0≤x≤β0,t∈J.假设对于x 使得在t∈J 上,有αn≤x≤βn 成立.令φ1=αn+1-x,φ2=x-βn+1,利用不等式(6)和BVP(7),可得
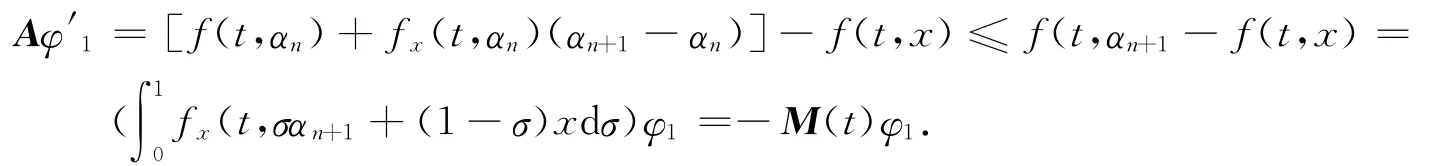
因Eφ1(0)=0和Fφ1(c)=0.由引理1,得αn+1≤x,t∈J.类似的,由条件A2)和BVP(8),可知
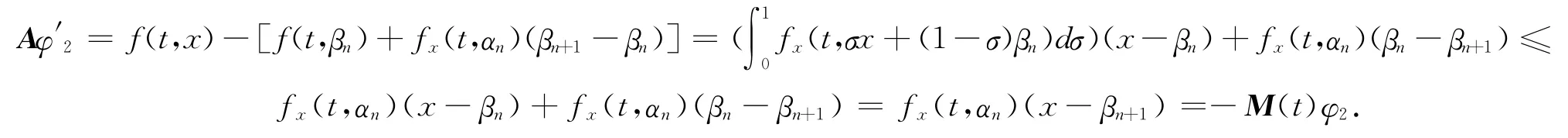
由引理1可推出x≤βn+1,t∈J.从而得出αn+1≤x≤βn+1,t∈J.由于α0≤x≤β0,通过归纳得出an≤x≤βn 对所有的自然数n 成立.从而有α0(t)≤α1(t)≤…≤αn(t)≤x(t)≤βn(t)≤…≤β1(t)≤β0(t),t∈J.
易证序列{αn(t)}和{βn(t)}是一致有界,同等连续的.利用Ascoli-Arzela定理,可得存在子序列{αn,j(t)},{βn,j(t)}使得αn,j(t)→ρ(t)和βn,j(t)→r(t)成立,其中ρ(t)≤x(t)≤r(t),t∈J.由于序列{αn(t)}和{βn(t)}是单调的,可以得出结论αn→ρ(t)和βn→r(t)成立.当n→∞,有
下面证明ρ(t)≥r(t).由条件A2),可知

通过引理1得到r(t)≤ρ(t).又因为ρ(t)≤r(t),t∈J.因此,ρ(t)≡r(t),即当偏导数fx存在且连续时,BVP(1)有唯一解.
最后,证明序列的平方收敛性.为此,设x(t)为BVP(1)在S(α0,β0)中的任一解,考虑pn+1(t)=x(t)-αn+1(t)≥0,t∈J,且注意到Epn+1(0)=0,Epn+1(c)=0.由BVP(7)和条件(A2),可知
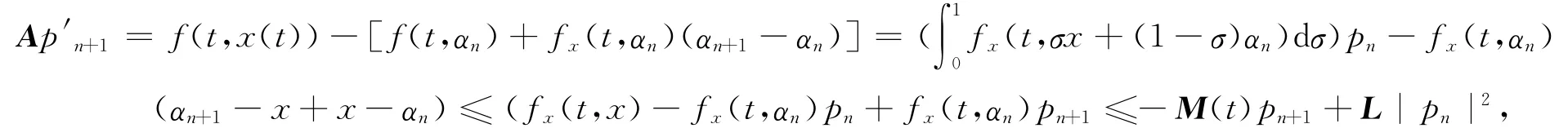
其中,|pn|2=(|pn1|2,|pn2|2,…,|pnn|2)T.因此,有
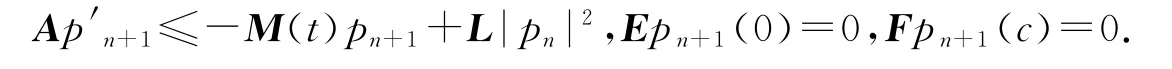
利用引理1得到pn+1(t)≤x(t),t∈J,其中x(t)是奇异线性系统Ax′+M(t)x=L|pn|2,Ex(0)=0,Fx(c)=0的解.因此,利用引理3 的表达式得,其中
通过计算有Q-1(-ζ1)≤Kmax|g(t)|成立,其中K 是非负矩阵.又ÂÂD≥0,可知t∈J,P 是非负矩阵.因此,通过合适的估计有,其中,K1是正矩阵…,|gn(t)|)T.
类似的,定义qn+1(t)=βn+1(t)-x(t)≥0,t∈J,注意到Eqn+1(0)=0,Fqn+1(c)=0.由BVP(8)和条件(A2),便有
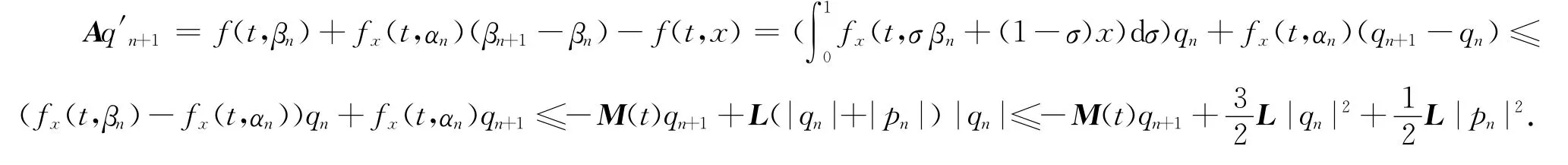
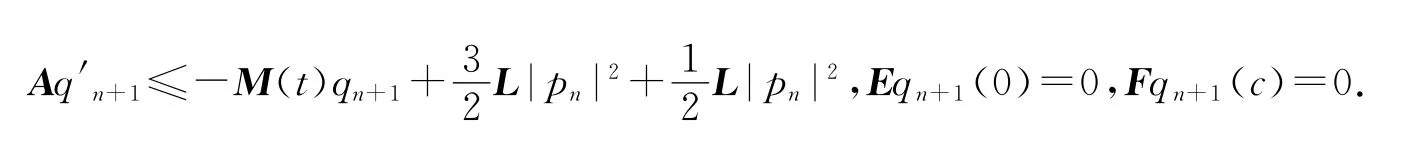
由引理1得qn+1(t)≤x(t),t∈J,其中x(t)是系统,Ex(0)=0,Fx(c)=0的解.因此,利用引理3中x(t)的表达式,并通过合适的估计有,其中K2和K3是正矩阵.证明完成.
当a=b=0,c=1时,边值问题(5)的解可表示为
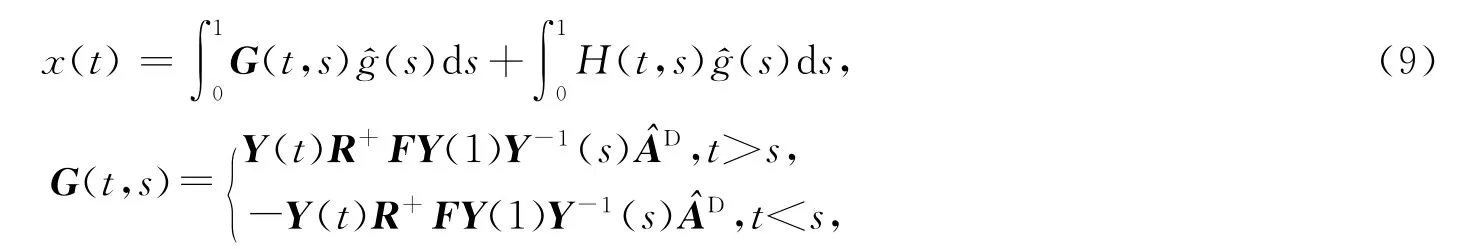

的基矩阵.类似定理1,可以得到单调序列一致且平方收敛到BVP(1)的解.
[1] ROSENBROCK H H.Structural properties of linear dynamical systems[J].Internat J Control,1974,200:191-202.
[2] CAMPBELL S L.Singular systems of differential equations[M].London:Pitman Advanced Publishing Program(I),1982.
[3] CAMPBELL S L.Singular systems of differential equations[M].London:Pitman Advanced Publishing Program(II),1982.
[4] BELLMAN R,KALABA R.Quasilinearization and nonlinear boundary value problems[M].New York:Elsevier,1965.
[5] LAKSHMIKANTHAM V,VATSALA A S.Generalized quasilinearization for nonlinear problems[M].Dordrecht:Kluwer Academic Publishers,1998.
[6] AHMAD B,ALSAEDI A.An extended method of quasilinearization for nonlinear impulsive differential equations with a nonlinear three-point boundary condition[J].Electron J Qual Theory Differ Equ,2007,1:1-19.
[7] WANG Peiguang,LI Ping.Kth order convergence for a semilinear elliptic boundary value problem in the divergence form[J].Appl Math Comput,2011,217:8547-8551.
[8] WANG Peiguang,WU Haixia,WU Yonghong.Higher even-order convergence and coupled solutions for second-order boundary value problems on time scales[J].Comput Math Appl,2008,55:1693-1705.
[9] DEVI J V,MCRAE F A,DRICI Z.Generalized quasilinearization for fractional differential equations[J].Comput Math Appl,2010,59:1057-1062.
[10] WANG Peiguang,HOU Ying.Generalized quasilinearization for the system of fractional differential equations[J].J Funct Spaces Appl,2013:793263.
[11] ABD-ELLATEEF KAMAR A R,ATTIA G M,VAJRAVELU K,et al.Generlized quasilinearization for singular system of differential equations[J].Appl Math Comput,2000,114(1):69-74.
[12] EL-GEBEILY M,OREGAN D.Upper and lower solutions and quasilinearization for a class of second order singular nonlinear differential equations with nonlinear boundary conditions[J].Nonlinear Anal Real Word Appl,2007,8:636-645.
[13] WANG Peiguang,KONG Tiantian.Quasilinearization for the boundary value problem of second-order singular differential system[J].Abstr Appl Anal,2013:308413.
[14] 奚宏生.连续时间广义边值系统的状态结构[J].控制理论和应用,1993,10(6):692-697.XI Hongsheng.On the state of continuous-time boundary value descriptor systems[J].Control Theory Appl,1993,10(6):692-697.
