不对称半桥反激变换器的设计

廖鸿飞+梁奇峰+熊宇

摘 要： 为了提高充电器效率和简化电路结构，采用不对称半桥反激式变换器作为锂电池充电器的主电路，详细分析不对称半桥反激变换器的工作原理和软开关条件，给出主电路参数之间的关系式，并利用关系式设计150 W样机进行实验验证；实验结果表明，所有功率器件均实现了软开关。采用不对称半桥反激变换器设计的锂电池充电器具有结构简单，效率高，电磁干扰小的优点。

关键词： 不对称半桥； 反激变换器； ZVS； 软开关条件

中图分类号： TN720?34 文献标识码： A 文章编号： 1004?373X（2015）14?0149?03

0 引 言

传统的反激变换器由于结构简单，成本低等特点在充电器设计中得到了广泛应用，然而由于反激变换器的开关元件工作在硬开关状态，效率低，EMI干扰大[1]，因此不适合于大功率场合的应用。不对称半桥变换器是一种新型的软开关变换器，效率高，EMI干扰小，但是结构较为复杂，并且变压器容易出现偏磁而导致损坏。

不对称半桥反激变换器结合了反激变换器及不对称半桥的优点，利用变压器的漏感与隔值电容的谐振，使得原边开关管实现了ZVS，副边二极管工作于ZCS状态，因此开关损耗和EMI干扰得到了大幅度的减小，并且由于变压器工作于反激状态，克服了不对称半桥变换器偏磁的缺点，使得不对称半桥反激变换器受到了学者的关注。

本文对不对称半桥反激的工作原理及参数设计进行了详细分析，并设计了150 W的实验样机，对不对称半桥反激变换器的参数设计及性能进行了验证。

1 不对称反激半桥变换器的工作原理分析

1.1 变换器工作模态分析

不对称半桥反激变换器的结构图[2]如图1所示，该图中Vin为直流输入电压；开关管 Q1和 Q2为变换器中半桥结构的2个开关管，Q1，Q2为互补驱动，DS1和 DS2分别为开关管 Q1和 Q2的体二极管；CS1和 CS2为开关管Q1和 Q2的寄生电容；Cr为隔直电容；Lm为励磁电感，Lr为变压器漏感，变压器的变比为n；输出端D为副边整流二极管，C为输出滤波电容，R为负载。

图1 不对称半桥反激变换器的结构图

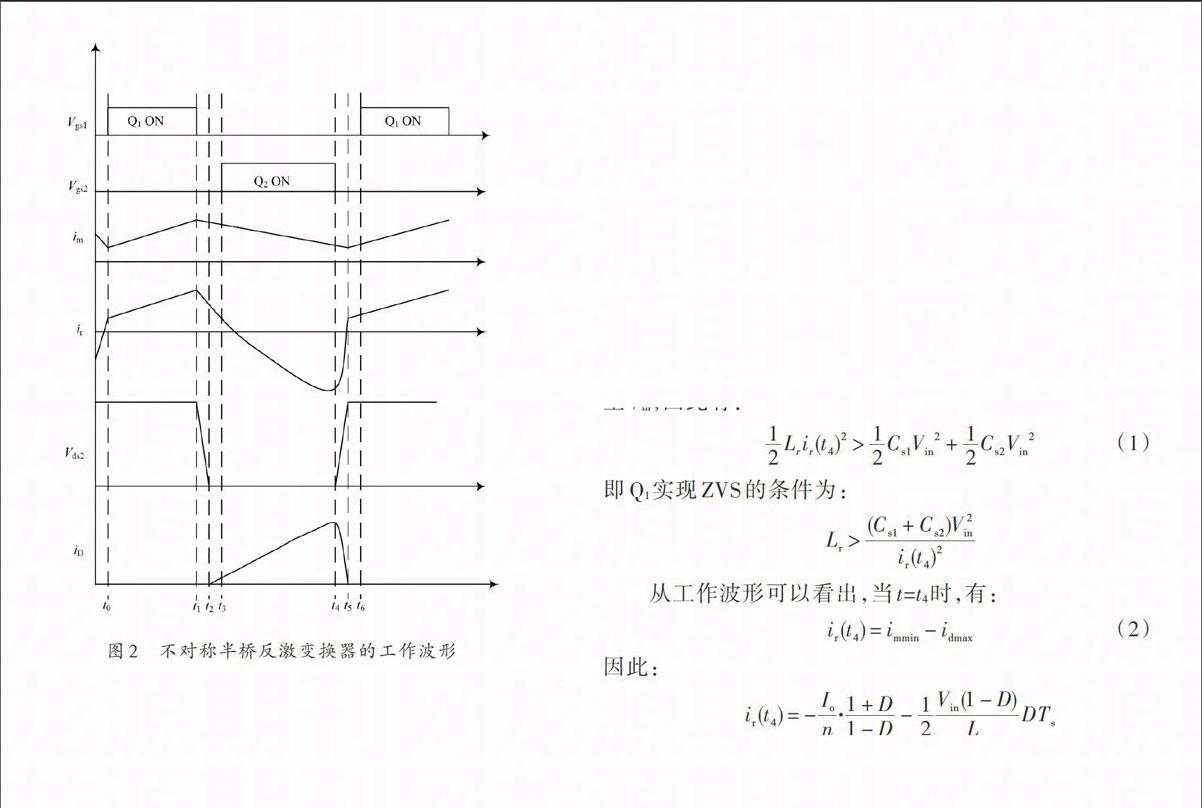
不对称半桥反激变换器的工作波形如图2所示，在一个开关周期中，不对称半桥反激变换器有6种状态[3]。

图2 不对称半桥反激变换器的工作波形

状态1（t0～t1）：当t=t0时，变换器上管Q1导通，Q2断开，Q2的D?S间电压为Vin，变压器原边电压为正，副边二极管反偏截止；此时Lr和Lm串联，在输入电压作用下，电流线性上升，变压器存储磁场能量。输出滤波电容向负载提供能量。

状态2（t1～t2）：当t=t1时，Q1关断，由于ir为正，此时，ir将给Q1的寄生电容Cs1充电，给Q2的寄生电容Cs2放电，使得Q1的D?S间电压Vds1线性上升，Q2的D?S间电压Vds2线性下降。当t=t2时，Vds2下降到零。

状态3（t2～t3）：当t=t2时，Vds2下降到零，而ir为正，因此，Q2的寄生二极管Ds2导通，此时若施加驱动信号于Q2的栅极，Q2将实现零电压开通，即ZVS。当Vds2下降到零，变压器激磁电感两端电压将反向，副边二极管D将正偏导通，Lm两端的电压将箝位在nVo。变压器的漏感Lr与隔值电容Cr发生谐振，存储在励磁电感中的能量将向副边传递，由于副边电流的存在，原边电流ir与励磁电感电流im不相等。

状态4（t3～t4）：当t=t3时，施加驱动信号于Q2的栅极，Q2零电压开通，原边漏感Lr与Cr谐振，输出电路维持导通，输出电流iD开始增加。

状态5（t4～t5）：当t=t4时，Q2关断，为了防止Q1，Q2同时导通，Q1，Q2同时保持关断。初级电流ir给开关管Q1的，初级电流 ir给开关管 Q1的反并联电容 CS1放电，同时给开关管 Q2的寄生电容CS2充电，变压器初级电流ir开始正向增大，当t=t5时，Cs1放电完毕，Vds1下降到零。

状态6（t5～t6）：当t=t5时，Cs1两端电压下降到零，原边电流ir开始流过Q1的寄生二极管Ds1。同时原边电流ir近似线性增加，当t=t6时，给Q1栅极施加驱动信号，Q1导通，此时Q1为零电压导通。当t=t6时，励磁电感电流im与漏感电流ir相等，副边二极管D内电流为零时自然关断，即实现了ZCS。

1.2 软开关条件分析

1.2.1 Q1的ZVS条件

由状态5和状态6的分析可知，要使得Q1实现ZVS，Lr必须有足够的能量，使得Q1寄生电容Cs1两端的电压从Vin被放电至零，Q2的寄生电容Cs2两端的电压[4]被充电至Vin，因此有：

[12Lrir（t4）2>12Cs1Vin2+12Cs2Vin2] （1）

即Q1实现ZVS的条件为：

[Lr>（Cs1+Cs2）V2inir（t4）2]

从工作波形可以看出，当t=t4时，有：

[ir（t4）=immin-idmax] （2）

因此：

[ir（t4）=-Ion·1+D1-D-12Vin（1-D）LmDTs]

1.2.2 死区时间的选取

为了防止Q1，Q2直通，在Q1与Q2驱动信号之间需要加入死区时间。在死区时间内，原边电流给Q1，Q2的寄生电容进行充放电，以实现软开关，因此死区时间必须大于Q1，Q2寄生电容的充放电时间，以保证Q1，Q2能实现软开关，能够实现零电压开通的的最小死区时间为：

[tdead>maxCsVinir（t1），CsVinir（t4）]

当Q1，Q2的寄生电容充放电完毕，而Q1，Q2的栅极仍未施加驱动信号时，原边电流将通过Q1，Q2的体二极管流动，即状态3和状态6，由于Mosfet的体二极管的压降通常比较大，将造成较大的损耗，因此需要合理选择死区时间，尽量缩短状态3和状态6的时间。

2 参数计算

（1） 在整个变换器中个，变压器参数的设计是关键，对于磁性元件，应满足伏秒积分平衡法则，即励磁电压和时间的乘积等于去磁电压和时间的乘积，即：

[（Vin-Vcr）LmLm+LrDTs=nVo（1-D）Ts] （3）

由于电容电压不能突变，因此在稳态工作时，隔值电容上的电压基本保持固定，即：[Vcr=DVin]，因此变压器匝比为：

[n=DVinLmVo（Lm+Lr）] （4）

由电磁感应定律可得变压器原边匝数为：

[Np=VinD（1-D）AeΔBfs]

因此副边匝数为：

[Ns=Npn]

（2） 隔值电容的选取。当Q1关断后，谐振电感与隔值电容发生谐振，整个Q1关断间隔时间大约等于半个谐振周期，因此有：

[πLrCr=（1-Dmin）Ts]

解上式可得：

[Cr=（1-Dmin）2T2sπ2Lr]

3 实验验证

根据上述的参数设计方法，设计了150 W的充电器，输入电压为[Vin=390 V]，输出电压为[Vo=24 V]，输出电流为[Io=6 A]，开关频率为[65 kHz]，[Lr=32 μH]，[Lm=750 μH]，[Cr=3.3 μF]，变压器采用PQ32/30磁芯，采用L6591为控制芯片。

图3为Q2的驱动波形及DS的波形，Q1，Q2之间留有一定的死区时间。从波形中可见，Q2导通前，其DS电压已经下降到零，Q1，Q2均实现了ZVS。图4为二极管电流与电压波形，从图中可见，二极管关断前电流已经下降到零，副边二极管实现了ZCS。

图3 Q2驱动波形及DS波形

图4 整流二极管电压与电流波形

4 结 语

针对反激变换器开关损耗大，电磁干扰大的特点，将传统反激变换器与不对称半桥相结合，研究设计了一种不对称半桥反激变换器为主电路的锂电池充电器；分析不对称半桥反激变换器的工作原理和实现软开关的条件，给出了参数设计方法。实验结果表明，上述设计方法是切实有效的，不对称半桥反激变换器能很好地实现软开关，提高效率，减小电磁干扰。

参考文献

[1] CHO Junseok， KWON Joonggi， HAN Sangyoung. Asymmetrical ZVS PWM flyback converter with synchronous rectification for ink?jet printer [C]// 37th IEEE Power Electronics Specialists Conference. [S.l.]： IEEE， 2006： 1?7.

[2] LIN Bor?Ren， YANG Chengchang. Analysis， Design and Implementation of an asymmetrical half?bridge converter [C]// Proceedings of 2005 IEEE International Conference on Industrial Technology. [S.l.]： IEEE， 2005： 1209?1214.

[3] CHEN T M， CHEN C L. Analysis and design of asymmetrical half bridge ? flyback converter [J]. IEE Proceedings of Electric Power Applications， 2002， 149： 433?440.

[4] 廖鸿飞，帅定新，梁奇峰.反激变换器的原边非线性电流控制方法[J].现代电子技术，2013，36（6）：164?166.

[5] 刘鑫，王卫国，刘克承，等.星用基于UC1845多路输出双管反激开关电源设计[J].现代电子技术，2014，37（2）：159?162.

[6] 杨树涛，谷加臣，齐利，等.频率计算法设计RCC开关电源[J].现代电子技术，2011，34（24）：199?201.