企业横向竞争对供应链整体绩效影响

李锋魏莹

摘要：以多级供应链系统为对象，研究供应链内部成员企业之间的横向竞争对供应链整体运营绩效的影响。鉴于所研究问题的复杂特性，通过建立研究对象的多智能体模型，采用计算机仿真方法获取供应链的运营绩效指标值。研究结果表明供应链内部成员企业之间的横向竞争能够提高供应链系统的整体运营绩效。但是，对于竞争中处于弱势的企业而言，竞争会降低其收益。因此，可以通过收益共享等机制来实现供应链协调。

关键词：横向竞争；多级供应链；运营绩效；多智能体技术

中图分类号： F270 文献标志码：A 文章编号：1009-055X（2015）01-0015-07

一、引言现实世界中的供应链系统绝大多数是由多个制造商，分销商，批发商，或者多个零售商组成的供应“网络”，而不是简单的供应“链”。在此网络中，企业除了与上、下游企业之间存在着纵向竞争行为以外，还面临着与同级企业之间的横向竞争威胁。因此，研究复杂供应链中企业之间的横向竞争行为有着十分重要的现实意义。

二、国内外研究现状由于受到供应链网络结构复杂性引发的企业决策行为复杂性制约，当前在供应链管理研究领域中，主要以一些简单的二级供应链网络为研究对象，并多采用博弈论方法进行具体问题的数学建模与分析。其中，代表性的工作包括：Bernstein等人研究了一个供应商和多个相互竞争的零售商组成的二级供应链系统中零售商订货价格和订货量对系统绩效的影响[1]；Cachon等人对比分析了一个供应商和多个零售商组成的二级供应链情境下收益共享契约、价格折扣契约、回购契约等多种契约的效率[2]；Ha等人研究两个供应商和一个顾客之间的就产品价格和发货频率展开的三阶段非合作博弈，指出了发货频率提高能够提升供应商的竞争力等结论[3]；孙多青和马晓英分析了多个零售商下逆向供应链中的定价策略和利润分配问题[4]；陈敬贤等人以零售商之间的横向货物转运为研究对象，采用随机规划方法计算最佳的订货点[5]；陈兆波等人应用动态投影系统理论分析了多供应商、多零售商组成的供应链网络下制造商之间、零售商之间的博弈行为，并计算了产品供应量、服务水平等决策变量最佳值[6]；侯琳琳和邱菀华分析了零售商之间价格博弈对供应链绩效的影响，并分析了收益共享契约的有效性[7]；刘春林研究了一个供应商和多个竞争零售商构成的二级供应链系统的线性转移支付契约设计问题[8]；刘丽文等人分析了一个供应商、多个同质零售商组成的供应链系统下，传统库存管理、信息共享和供应商管理库存三种模式下供应链整体运作绩效[9]等。

由于供应链网络结构的复杂性，不同的成员企业在系统中的地位和相互关系各不相同，数学建模分析成员企业之间的交互对系统整体绩效的影响非常困难。进而，在此建模分析基础上寻找企业之间博弈解极其困难。因此如前所示，传统的数学建模分析通常分析一些结构简单、关系简单的供应链网络问题。近年来，随着计算机仿真技术的发展，一些专家也逐步尝试采用计算机建模与分析方法对此问题进行研究。例如，黎继子等人应用系统动力学仿真方法分析了两个二级供应链为满足集群市场需求而产生的零售商之间的产品调运问题[10]；Li采用多智能体建模方法为供应链网络中每位成员企业建立其智能体决策模型，并采用仿真方法研究了系统的运行绩效问题[11]；刘红和王平采用系统动力学建模方法仿真了多级供应链系统中的牛鞭效应现象[12]；Marquez等人采用系统动力学建模方法仿真分析了四级供应链中不同范围内信息共享条件下的企业绩效[13]等。

总的来说，当前对于供应链成员企业横向竞争研究还不成熟，不足之处如下：1）前人的研究工作主要以二级供应链系统为对象，对于多级供应链系统的研究工作还不多见；2）以多级供应链系统为对象的前期研究工作，很少考虑成员企业之间博弈行为，多以合作为主，如转运问题；3）考虑供应链成员企业的横向竞争行为时，多以企业自身利润最大化或成本最小化为目标，很少从供应链整体视角考虑供应链协同问题。而本文则采用多智能体建模与仿真方法，自底向上地建立多级供应网络的系统模型。通过系统仿真，分析供应链系统中企业间的横向竞争对供应链系统的整体绩效的影响和作用。

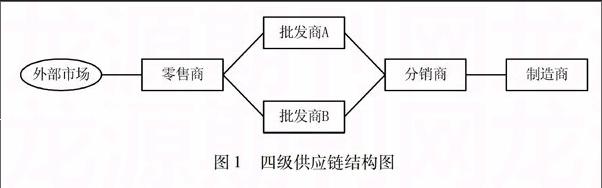
三、四级供应链模型在前期工作[11，14]基础上，本文以图1所示的四级供应链为研究对象，主要研究两个批发商之间的横向竞争行为对供应链整体绩效的影响。

该供应链系统由一个零售商，两个非同质、独立的批发商A和批发商B，一个分销商，和一个制造商组成，服务于外部市场的产品需求。在供应链系统内部，零售商将根据批发商A、B的各自产品报价决定它们的订货量，即批发商A和批发商B通过产品的批发价格进行博弈，以获得订单。

在此四级供应链系统的多智能体仿真模型中，每一个智能体代表一个成员企业。在每一个仿真周期中，“批发商A”智能体、“批发商B”智能体、“分销商”智能体的行为可以描述为：

1）收到来自供应链上游发来的产品，以及供应链下游发来的产品订货需求；

2）利用上游发来的产品和当前企业的产品库存满足下游的本期产品需求以及历史缺货累计量，即发货；

3）进行下一期的产品需求预测，并结合现有库存量和缺货量，向上游企业发出本期的产品订货需求。

“零售商”智能体将根据本期批发商A、B的各自产品报价决定向它们下发的订货量，具体为：

1）收到来自批发商A、B发来的产品，以及“外部市场”智能体发来的产品订货需求；

2）利用批发商A、B发来的产品和企业的库存产品满足“外部市场” 智能体的本期产品需求以及历史缺货累计量，即发货；

3）进行下一期的产品需求预测，并结合现有库存量和缺货量，确定本期的产品订货需求；

4）根据批发商A、B的产品报价，确定各自本期的订货需求。

由于本模型不考虑制造商的产能约束问题，即来自“分销商”智能体的产品订货需求总能够被满足，因此在每一个仿真周期中，“制造商” 智能体的行为可以描述为：

1）收到“分销商”智能体发来的产品订货需求；

2）利用本期生产出的产品和企业的库存满足“分销商”智能体的本期产品需求以及历史缺货累计量；

3）进行下一期的产品需求预测，并结合现有库存量和缺货量，制定本期的产品生产计划。

具体来说，该四级供应链模型中各智能体的参数设置如下：

公式（6）-（7）中，OAt、OBt分别代表第t期批发商A、B的订货量，IAt-1、IBt-1分别代表第t-1期末批发商A、B的缺货量。

零售商的初始库存量为20，安全库存量为10，且其发往外部市场的产品能够立即到达。

批发商A的初始库存量为14，安全库存量为10（由批发商A发往零售商的产品要经过2个单位的时间延迟才能到达）。

批发商B的初始库存量为6，安全库存量为5（由批发商B发往零售商的产品要经过2个单位的时间延迟才能到达）。

分销商的初始库存量为20，安全库存量为20（分销商发往批发商A和B的产品要经过2个单位的时间延迟才能到达）。

制造商的初始库存量为20，安全库存量为25。制造商的生产周期为2，且发货延时为2期。由于制造商有足够的生产产能，因此分销商的订货总将在5期之后到达。

四、批发商之间的横向竞争博弈本模型中考虑批发商A和B通过每期的产品报价进行竞争，而零售商则根据批发商的各自报价决定本期的向批发商A和批发商B各自下发的订货量。

假定零售商制定了一个产品的标准价格p，批发商A可以选择产品的价格为标准价格p，或者打折价095·p；而批发商B也有两种报价，一种是标准价格p，另一种是打折价09·p。

根据批发商的不同报价组合，零售商分配订货需求如表1所示。

由公式（8）和公式（9）的计算结果可得到混合策略纳什均衡解：在系统仿真运行中，每期中“批发商A”智能体将以3/4的概率选择报价为095·p，1/4的概率选择报价为p，从而获得最大的期望收益；而“批发商B”智能体则以3/7的概率选择报价为09·p，4/7的概率选择报价为p，从而获得最大的期望收益。

为了对比分析成员企业竞争对供应链系统整体绩效的影响，本文同时仿真分析以下两种情况：

1）供应商A和供应商B不采取竞争行为，因此零售商总是将70%的订货量分配给供应商A，而剩下的30%给供应商B。

2）供应商A和供应商B采取针锋相对策略（Tit-for-Tat）进行竞争：开始时都选择标准价格p。此后，供应商A和B都根据对方的前一次竞争策略制定对自己更有力的竞争策略[16]。

在针锋相对策略下，假定第n-1期供应商A和B都选择标准价格p，即策略为（p，p）。由表2数据可知，第n期时供应商A会选择标准价格p从而希望获得07·Ot·p的收益；而供应商B会选择打折价09·p，从而希望得到0315·Ot·p的收益。因此，零售商根据供应商A和B的本期报价（p，09·p），将65%的订货量分配给供应商A，而剩下的35%给供应商B。依此分析，可以得到供应商A和B的竞争策略为以下四个策略组合的顺序循环，即（p，p）→（p，09·p）→（095·p，09·p）→（095·p，p）。根据供应商A和B的竞争策略，可以零售商分配给供应商A和B的订货量为顺序循环：（07，03）→（065，035）→（07，03）→（0725，0275）。

五、供应链系统绩效指标参考评价供应链系统绩效的SCOR模型，本文以供应链订货需求的波动、需求满足率以及库存成本等成本指标作为衡量供应链系统绩效的指标集合[17]。具体来说，这些指标包括：

1）需求波动：供应链成员企业的订货（生产）量时间序列的方差与外部市场的需求时间序列的方差比值，即牛鞭效应指标值[18]：

从供应链系统角度上讲，各成员企业的牛鞭效应指标值越小越好。

此处需要特别指出的是，由于批发商A、批发商B每期获得的仅是来自零售商的部分订货量，因此，批发商A、批发商B的牛鞭效应指标值明显低于分销商，也明显低于零售商。从该数据上并不能直观反映出外部市场需求在批发商环节被放大，但是，可以对比不同情景下该指标值的大小。

2）准时交货率：供应链成员企业按照公式（4）发货。其中发货量为Ot-It-1，或者为Ot的次数Ci占总发货次数Ct的比例，即：

公式（14）中，常数项ch代表单位产品一期的库存成本，cp代表单位产品一期的缺货成本。

六、仿真结果分析作者在开放性多智能体系统仿真开发平台-REPAST（http：//repastsourceforgenet）基础上开发实现了前文所述的四级供应链系统。

由于系统仿真模型中外部市场需求中包含随机变量，且批发商A和B采取的最优混合竞争策略也存在随机概率，因此各模型的仿真重复100次（仿真周期为1000），记录每一次仿真得到的供应链系统的各项绩效指标值，并以100次仿真结果的平均值作为系统绩效评价值。

如前文所述，在仿真研究供应链系统中批发商A和批发商B之间的竞争博弈情景中，本文总共仿真和对比分析三种情景下的供应链系统绩效指标：

情景1：批发商A和批发商B无横向竞争；

情景2：批发商A和批发商B采取“针锋相对”的博弈策略；

情景3：批发商A和批发商B采取混合策略纳什均衡解的博弈策略。

三种情景下需求波动的量化指标-牛鞭效应值统计结果如表3所示。

从表3中的数据可知，当批发商A和B存在横向竞争关系时，供应链中的零售商、分销商和制造商的需求波动情况都有明显下降。并且，在竞争中处于强势的批发商A的需求波动也得到下降，而处于弱势的批发商B的需求波动却得到放大。此仿真结论符合供应链管理中对风险分担策略（risk pooling）的分析，即当批发商A和批发商B的订货需求时间序列的相关系数降低时，其上游企业的需求波动会有所减少[19]。

同时，当批发商A和批发商B采用理性策略（混合策略纳什均衡）进行博弈时，供应链中的零售商、分销商和制造商的需求波动要小于采用“针锋相对”策略博弈下的需求波动。同样，在竞争中处于强势的批发商A的需求波动也得以下降，而处于弱势的批发商B的需求波动却得到放大。

仿真数据表明：从需求波动的角度来说，供应链中处于弱势的企业不愿意与强势企业竞争，因为竞争关系的出现将导致其需求波动变大；而供应链中的强势企业，以及其他节点上的企业则倾向于通过竞争来降低需求波动。

表4给出了三种情景下的供应链各节点企业的服务水平-准时交货率指标数据。

从表4中的数据可以看出，除了批发商B以外的其他供应链节点企业，在有竞争关系的状态下，准时交货率都有所提高。并且竞争关系的存在，对下游企业的影响程度要大于对上游企业的影响程度。

并且，当企业采用理性策略进行博弈时，所有企业的准时交货水平都要高于“针锋相对”策略下的准时交货水平。

表4数据表明：从准时交货的角度来说，供应链中处于弱势的企业也不愿意与强势企业竞争，因为竞争关系的出现将导致其对下游客户（零售商）供货的准时交货率降低；而供应链中的强势企业，以及其它节点上的企业则倾向于通过竞争来提高准时交货率。

此结论也符合对表3的数据分析：竞争关系的存在导致了批发商B的需求波动增加，且由于其采用移动平均法预测未来一期的需求，因此其供货时的准时交货率下降；而其它企业则因为需求波动降低，移动平均法预测需求的精度提高，所以其准时交货率提高。

表5给出了三种情景下的供应链各节点企业的库存成本统计量-相对平均库存率指标数据。

从表5中的数据可以看出，存在竞争关系将降低供应链所有成员企业的库存成本。并且，理性策略下的竞争，能够更加有效地降低企业的库存成本。

同时，表6给出了三种情景下的供应链各节点企业的缺货成本统计量-相对平均缺货率指标数据。

从表6中的数据可以看出，存在竞争的环境下，零售商、批发商A、分销商和制造商的缺货率也有所降低；而批发商B的缺货率有所增加。并且，当企业（批发商A和批发商B）采用理性策略进行竞争时，零售商、批发商A、分销商和制造商的缺货率更低；而批发商B的缺货率更高。

结合表5和表6的数据可以表明：从库存成本的角度上说，理性的竞争能够有效地降低供应链中零售商、批发商A、分销商和制造商的成本。而对于批发商B来说，竞争使得其需求波动增加，“供不应求”的现象出现更多，因此其准时交货率也相应下降。

通过以上的三种情景下供应链系统绩效的仿真，可以得到；对于供应链内部竞争中的弱势企业而言，竞争将降低其自身的运营绩效—服务水平、库存成本、缺货率/缺货成本；但是对于供应链中的其它企业而言，引入了内部的竞争机制，都能够有效地提高它们的运营绩效。因此，从提升供应链整体绩效角度出发，可以通过引入竞争机制提高系统的整体运行绩效。对于由于竞争而利益受损的成员企业，其损失的利益可以由竞争而获利的成员企业进行利益的补偿。从供应链协调的视角，此情景下通过对因引入内部竞争机制而 “额外”获利的供应链内部企业的二次分配，使得最终供应链内部所有企业都因此而受益，即通过收益共享（profit—sharing）形式的供应链契约实现供应链绩效改善和协调。[20]对于此类供应链契约的具体形式，本文不继续讨论。具体来说，对仿真结果进行数据分析可以得出以下结论：

1）供应链内部的横向竞争能够抑制供应链中牛鞭效应现象，即需求波动的逐级放大。需求波动的降低，从而能够提高企业的服务水平-准时交货率，并能够降低成本（库存成本和缺货成本）。

2）对于竞争中的弱势企业，竞争关系的存在会增加其成本，并降低其服务水平。

3）由于存在横向竞争的供应链网络中除去竞争中弱势企业的运营绩效有所下降外，其他企业都有所上升，因此可以通过收益共享机制实现利润在供应链内部企业的二次分配，通过补偿弱势企业的一定损失来实现整个供应链系统的协调。

因此，对于现实中的供应链系统而言，本文研究结果表明可以普遍地通过引入供应链内部成员企业的竞争机制来提升系统的整体运营绩效。对于由于引入内部竞争而因此受损的成员企业，其损失的利益部分可以由因此获益的成员企业共同补偿，从而实现所有企业都能因此受益。

七、结论供应链网络中成员企业之间的横向和纵向竞争行为普遍存在，且会对供应链系统整体运作产生影响。但是，由于供应链系统的系统复杂性，以及企业竞争中采取的策略的主观性，传统的数学建模与分析的方法难以适用于研究此类问题。因此，本文应用多智能体建模方法建立问题模型，并通过计算机仿真来分析和量化横向竞争行为对供应链整体绩效的影响。

对于本文所研究的一个典型四级供应链系统来说，横向竞争将提高供应链系统的整体绩效水平，以及各成员企业的绩效水平（除了竞争中处于劣势位置的批发商B以外）。从此仿真结果可以知道，在保持供应链现有结构和关系不变的前提下，竞争行为是被供应链中的成员企业默许的。而在竞争中处于劣势的企业则可以通过供应链收益共享机制分享竞争带来的收益。参考文献：

[1] Bernstein F， Federgruen A. Decentralized Supply Chains with Competing Retailers Under Demand Uncertainty[J]. Management Science. 2005， 51（1）： 18-29.

[2] Cachon GP， Lariviere MA. Supply Chain Coordination with Revenue-Sharing Contracts： Strengths and Limitations[J]. Management Science. 2005， 51（1）： 30-44.

[3] Ha AY， Li L， Ng. SM. Price and Delivery Logistics Competition in a Supply Chain[J]. Management Science. 2003， 49（9）： 1139-1153.

[4] 孙多青，马晓英. 基于博弈论的多零售商参与下逆向供应链定价策略及利润分配[J]. 计算机集成制造系统. 2012， 18（4）： 867-874.

[5] 陈敬贤，王国华，梁樑. 供应链系统中零售商横向转载的随机规划模型及算法[J]. 系统工程理论与实践. 2012， 32（4）： 738-745.

[6] 陈兆波，滕春贤，姚锋敏. 考虑服务水平的供应链网络动态模型研究[J]. 管理工程学报. 2011， 25（1）： 121-127.

[7] 侯琳琳，邱菀华. 零售商价格竞争下供应链的均衡及协调研究[J]. 系统工程学报. 2010， 25（2）： 246-250.

[8] 刘春林. 多零售商供应链系统的契约协调问题研究[J]. 管理科学学报. 2007， 10（2）： 1-6.

[9] 刘丽文，赵会军，袁佳瑞. 一对多供应链在传统、信息共享和供应商管理库存模式下的绩效比较[J]. 计算机集成制造系统. 2007， 13（11）： 2154-2161.

[10] 黎继子，刘春玲，李伯勋. 集群式供应链跨链间的库存协调模型研究[J]. 系统工程与电子技术. 2007， 29（9）： 1479-1483.

[11] Li F. A Framework for Multi-Agent Based Supply Network Simulation[C]. In Proceedings of 2010 International Conference on Management and Service Science. 2010. 1-4.

[12] 刘红，王平. 基于ARMA（1，1）需求的多级供应链牛鞭效应仿真[J]. 系统仿真学报. 2008， 20（12）： 3253-3257.

[13] Marquez AC， Bianchi C， Gupta JND. Operational and Financial Effectiveness of E-collaboration Tools in Supply Chain Integration[J]. European Journal of Operational Research. 2004， 159： 348-363.

[14] 李锋，魏莹. 决策行为影响牛鞭效应的仿真研究[J]. 系统管理学报. 2011， 5：533-538.

[15] Li F. Modeling and Simulation of Supply Network Evolution and Revolution： A Multi-Agent Approach[C]. In Proceedings of 2010 International Conference on Artificial Intelligence and Computational Intelligence. 2010， 203-207.

[16] 蒋国银，胡斌. 集成博弈和多智能体的人群工作互动行为研究[J]. 管理科学学报. 2011， 14（2）： 29-41.

[17] 邓培，黎建强. 基于模糊评估和马尔科夫预测的供应链动态平衡记分卡[J]. 系统工程理论与实践. 2008， 4： 57-64.

[18] Chen F， Drezner Z， Ryan JK， Simchi-Levi D. Quantifying the Bullwhip Effect in a Simple Supply Chain： The Impact of Forecasting， Lead Times， and Information[J]. Management Science. 2000， 46（3）： 436-443.

[19] 唐凯，杨超，杨珺. 随机多阶段分销网络设计模型[J]. 中国管理科学. 2007， 15（6）： 98-104.

[20] Yan R. Profit Sharing and Firm Performance in the Manufacturer-Retailer Dual-Channel Supply Chain[J]. Electronic Commerce Research. 2008， 8（3）： 155-172.

Abstract： In this paper， a multiagent based simulation framework is proposed to model a multiechelon supply chain system， in which two heterogeneous distributors compete for retailers orders. Impact of horizontal competition on the supply chain performance is analyzed under different competition strategies， and further quantified by multiagent simulation approach. Results show that the horizontal competition behavior between two distributors can improve the performance of the whole supply chain system， which， however， reduces the performance of the weaker player in the competition. In this situation， profitsharing strategy should be utilized to achieve supply chain coordination.

Key words： horizontal competition； multiechelon supply chain； system performance； multiagent technology