基于PSO-SVM的PMV指标预测系统研究
2015-07-20赵敏华苏蕤徐立先
赵敏华苏蕤徐立先
1西安建筑科技大学信息与控制工程学院
2山东省科学院自动化研究所
基于PSO-SVM的PMV指标预测系统研究
赵敏华1苏蕤1徐立先2
1西安建筑科技大学信息与控制工程学院
2山东省科学院自动化研究所
随着空调应用的日益广泛,室内环境的热舒适性和空气品质越来越受到人们的关注。基于此本文研究了一种自适应粒子群支持向量机分类模型对室内热舒适度进行评价的方法,文中给出了模型的详细设计步骤和实现代码,并采用“智能建筑环境技术平台”的热舒适指标数据库中的夏季PMV数据集对模型进行仿真研究,且与基于网格搜索-SVM模型作了深入对比,实验结果表明PSO-SVM模型应用到室内环境舒适度评价具有一定优势。
热舒适指标 粒子群算法 支持向量机
0 引言
随着经济技术的发展和生活水平的不断提高,空调在工作、生活中越来越必不可少。研究表明:室内良好舒适的环境可以使人精神愉快、提高工作效率,适宜的热环境可提高生产率18%[1]。
与以往围绕“温度”这一单一影响人体舒适度指标的研究不同,本文选用了一个在环境舒适度研究领域内获得越来越高认可度和应用度的指标[2~5]——PMV,该指标包含空气温度、风速、穿衣指数等7个参数。与过去单纯以温度的高低来衡量环境是否舒适的方法相比,运用PMV指标进行评价的方法更加的全面和科学。
当然,在寻找(研究)这个问题解决方案的过程中,对环境的舒适度做出准确的预测首先就是一个非常重要的环节。本文以此为背景,建立了一种基于PSO-SVM的热舒适指标预测模型,并通过对实例的Matlab仿真验证了该模型的可行性。
1 支持向量机理论和粒子群优化算法
支持向量机算法(Support Vector Machine,SVM)是由Vapnik等提出的一种以统计学习理论为基础的新型机器学习方法。它以结构风险最小为原则,本质上是求解凸二次规划问题,其在解决小样本、非线性和高维模式识别问题中有较大优势。
SVM分类法基本思想是在样本空间中构造最优分类超平面,使得超平面与不同类别的样本集之间的距离最大,从而达到最大的泛化能力。支持向量机算法的实现与内积核函数有关[6]。
为了选择合适的核函数并确定最优的核函数参数,引入了粒子群优化算法 (Particle Swarm Optimization,PSO),该算法模拟鸟集群飞行觅食的行为,鸟之间通过集体地协作使群体达到最优目的,是一种基于Swarm Intelligence的优化方法。PSO算法中需要调整的参数较少,因而容易实现[7]。
2 数据的获取与预处理
本文的数据来自我校“智能建筑环境技术平台”的热舒适指标数据库中的夏季PMV数据集,该数据集包含有三种不同热舒适度的数据共199组样本数据,每个样本数据均由人体代谢率,人体对外做功,所着服装热阻、空气温度、空气流速、空气相对湿度、平均辐射温度共7个参数组成,也就是说每一组样本数据都是7维的。199组样本根据PMV值分为3类:PMV=1的26组、PMV=2的137组、PMV=3的36组,在此设定模型输出1,2,3分别表示三种热舒适度下的环境。从三类环境中共取99组样本作为训练样本,剩余的 100组作为测试样本。采用 Matlab中的mapminmax函数将输入数据归一化到[-1,1]区间,这样就完成了数据的预处理工作。
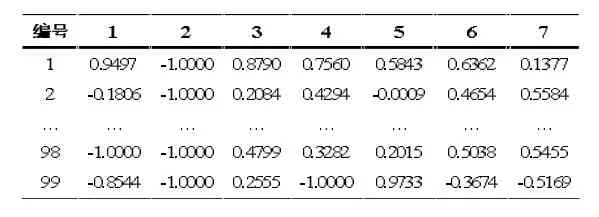
表1 训练样本输入数据
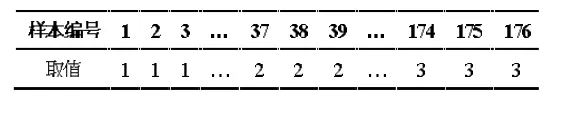
表2 训练样本输出数据
3 PSO-SVM模型的创建
3.1 SVM数学模型的构建
SVM方法完成分类主要分为以下3个步骤:①选定非线性映射K(x),这里是指PMV的计算公式;②将输入向量X通过K(x)映射到一个高维的特征空间Y中,这里输入向量X=[x1,x2,……,x199](xi∈R7),高维特征空间Y=[y1,y2,……,y199](yi=1、2或3);③在高维特征空间Y中寻找最优分类平面。
根据以上的理论,进行数学模型地构建。首先,设最优分类平面为ω·x+b=0,此时训练集应该满足yi(ω· xi+b)-1≥0,此时分类问题就可以转化为二次回归问题min(0.5||ω||2+c(Σδi)),其中yi(ω·xi+b)≥1+δi,δi≥0,c表示惩罚因子。随后通过引入拉格朗日因子将二次回归最小化问题转化为对偶规划问题max(ΣQi-0.5ΣQiQ·jxi),其中Qi和Qj表示拉格朗日因子。最后SVM的非线性判别函数就可以表示为f(x)=sgn(ΣQiyiK(xi,xj)+b)[8]。
以上理论是支持向量机进行模式分类的基本原理,实际上对其在Matlab环境下进行仿真,实现模型构建和结果分类,仅需要两条调用语句,即svmtrain和svmpredict。
3.2 PSO优化SVM参数的算法设计
图1为PSO优化SVM参数算法的基本流程。
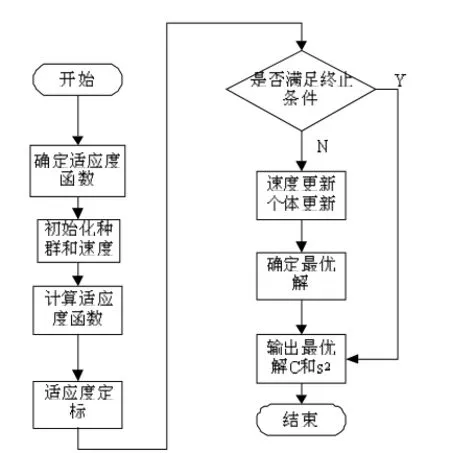
图1 PSO优化SVM参数算法的基本流程
Step 1:设定相关参数
①种群规模sizepop:由于在本文中需要优化的参数只有两个,即惩罚因子c和核函数的参数g,因此群体中均是由这两个参数组合而成的二维粒子(c,g),因此取sizepop=30并且设定搜索空间的维度是2。
②惯性权重ω:它是用来平衡全局搜索和局部搜索效果的参数,较大的ω有利于群体在更大的范围内进行搜索,而较小的ω能够保证群体收敛到最优位置,本文将ω设定为0.8。
③学习因子c1和c2:它们用于调整单个粒子在群体寻优过程中,自身经验和社会经验在其运动中的作用,表示每个粒子向pbest和gbest位置的随机加速项的权重。如果c1=0,则代表粒子自身没有认知能力。如果c2=0,代表粒子没有进行群体信息共享,一般c1和c2的取值范围为[0,4][9],本文设定c1=c2=2,交叉验证的参数k=3。
Step 2:初始化种群和速度
①在确定PSO的相关参数和搜索维度后,在Matlab中进行种群和速度初始化的语句如下:
pop(i,1)=(popcmax-popcmin)*rand+popcmin;
pop(i,2)=(popgmax-popgmin)*rand+popgmin;
V(i,1)=Vcmax*rands(1);
V(i,2)=Vgmax*rands(1);
其中,popcmax=102,popcmin=10-1,popgmax=103,popgmin=10-2。
②计算初始适应度:
cmd=‘[-v’,num2str(v)‘,-c’,num2str(pop(i,1))‘,-g’, num2str(pop(i,2))];
fitness(i)=svmtrain(train_pmv_labels,train_pmv, cmd);
fitness(i)=-fitness(i);
Step 3:迭代寻优;
①极值更新[10]:比较粒子个体的适应度值fitness (j)和其经历过的最好位置的适应度值local_fitness(j),若前者小于后者,则将后者的值赋给前者。再比较新的粒子个体适应度值和所有群体所经历的最好位置的适应度值,此时若前者小于后者,则将后者的值赋给前者。Matlab中的部分代码如下:
个体最优更新:
if fitness(j)<local_fitness(j)
local_x(j,:)=pop(j,:);
local_fitness(j)=fitness(j);
群体最优更新:
if fitness(j)<global_fitness
global_x=pop(j,:);
global_fitness=fitness(j);
②速度更新:以①生成的两个极值为基础,采用Matlab编写的部分程序如下:
V(j,:)=wV*V(j,:)+c1*rand*(local_x(j,:)-pop(j,:)) +c2*rand*(global_x-pop(j,:));
Step 4:自适应变异;
考虑到种群更新过程中粒子变异的幅度对全局搜索能力和局部搜索能力可能会产生影响,因此本文引入了自适应变异策略,并取粒子变异率为0.5,对所有的粒子分配一个随机数rand,采用Matlab编写的部分程序如下:
if rand>0.5
k=ceil(2*rand);
if k==1
pop(j,k)=(20-1)*rand+1;
if k==2
pop(j,k)=(popgmax-popgmin)*rand+popgmin;
Step 5:迭代终止判断;
判断程序的运行是否达到了设定的最大迭代次数maxgen(maxgen=200)。如果达到了,则输出最优的粒子,并将得到的最好的c和g值赋给支持向量机,进入接下来的预测分类环节;如果没有达到,则返回Step3,继续进行下一轮寻优过程,直到满足终止条件。
4 仿真实验
4.1 SVM模型对样本的预测
由图2可以看出,采用SVM模型对100组测试样本进行分类的结果准确率很低,只有69%,远不能满足课题对于样本准确分类的需求。这说明引入优化算法,为SVM模型选择合适的c和g非常有必要。
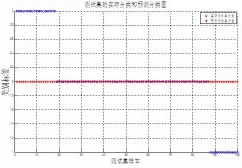
图2 基于SVM模型的识别结果
事实上,如何选择适合模型的优化算法也是一个值得研究的课题,下文中将采用两种比较典型的算法来优化已有模型,并将优化结果进行比对,找到最适合的优化算法。
4.2 基于PSO-SVM模型对样本的预测
考虑到PSO算法中的rand对实验结果的影响,也为了使仿真结果更具说服力,将该模型运行了10次,发现各次运行得到的c和g的值都是一样的,并且最终样本预测的准确率都可以达到100%。下面以其中一次的运行结果进行说明。PSO算法寻优过程中的适应度变换曲线如图3所示,PSO算法寻找最优c和g的过程如图4所示,基于PSO-SVM模型的分类结果如图5所示。
图3说明PSO算法可以较快地找到最优解,即bestc和bestg;图4中由于寻优曲线很密集,没办法直观地看到bestc和bestg的位置,但是这在Matlab的command窗口中是有结果输出的:best=1,best= 0.0625,bestacc=100。这里的bestacc=100指的是K-折交叉验证过程中的最高精度是100%。从图5可以看出,PSO-SVM模型对100组测试样本进行分类,准确率可达100%。
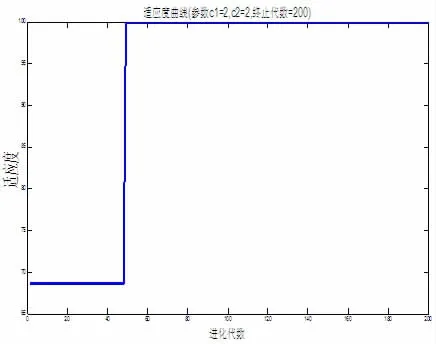
图3 PSO算法适应度变换曲线

图4 PSO算法优化bestc.bestg的轨迹
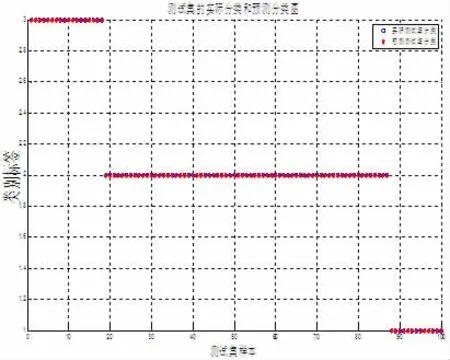
图5 基于PSO-SVM模型的识别结果
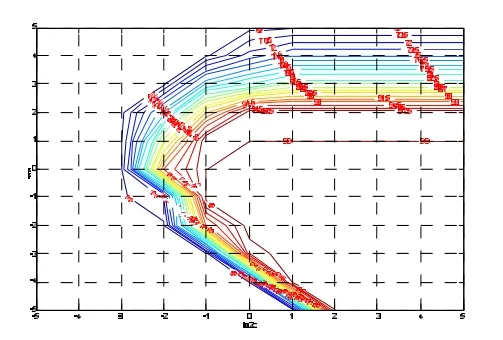
图6 网格搜索法优化bestc,bestg的轨迹
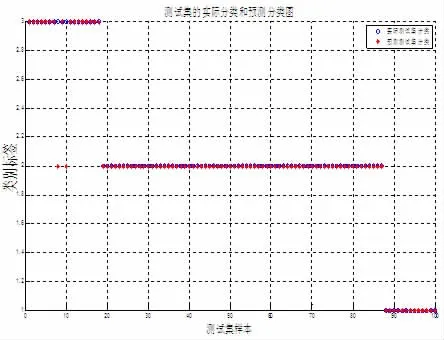
图7 基于网格搜索-SVM模型的识别结果
4.3 基于网格搜索-SVM模型对样本的预测
为了进一步说明PSO-SVM模型的优越性,同时证明PSO算法的引入对于SVM模型参数选取的有利影响,将网格搜索法也引入到了SVM模型的参数选取中,同样将基于网格搜索-SVM模型运行10次,发现每次得到的bestc和bestg都有一定的差异,而样本的分类结果准确率在96.73%~98.00%之间,网格搜索法寻找bestc和bestg的过程如图6所示(bestc=0.5,bestg=2.225,bestacc=99),基于网格搜索-SVM模型运行10次中最优1次的分类结果如图7所示。
4.4 PSO-SVM模型和网格搜索-SVM模型的对比
表3给出了两种模型10次运行的平均时间和预测准确率,从表中可以看出PSO-SVM模型的平均预测准确率高于网格搜索法-SVM模型2.635%,但是前者运行时间却比后者长9.4802s,但是考虑到当前计算机的智能化程度和运算速度,这种级别的时间差几乎不会给计算机的运行带了额外的负担,因而引入PSO算法进行更精准的预测还是很有必要的。

表3 两种模型预测结果对比
5 结语
本文研究了基于PSO-SVM模型的环境舒适度评价模型,文中给出了在Matlab环境下创建该模型的详细步骤及实现代码。最后的仿真结果证明了PSO算法引入的有效性,也证明了将PSO-SVM模型应用到室内环境的舒适度预测是可行的,此模型也可应用到其他领域,用来解决相关的分类预测问题。
[1]罗婷.基于PMV指标的室内热舒适控制方法的应用研究[D].济南:山东建筑大学,2009
[2]牛润萍,陈其针,张培红.热舒适的研究现状与展望[J].人类工效学,2004,10(1):38-40
[3]王丹,曹红奋.基于PMV控制目标的舒适性空调应用研究[J].洁净与空调技术,2011,3(1):8-11
[4]郭富军,杨昌智.舒适指标在空调系统控制中的应用研究[J].湖南大学学报,2000,2(9):761-764
[5]魏东,潘兴华,张明廉.舒适性指标PMV在暖通空调控制中的应用[J].北京建筑工程学院学报,2004,20(1):52-56
[6]王兴芬,李雪燕,张继松.基于支持向量机的网上银行验证码识别研究[J].计算机工程与应用,2012,1(6):1-7
[7]王海军,乔烨.PSO-SVM模型在葡萄酒品质分类中的应用研究[J].计算机与数字工程,2012,40(8):146-148
[8]黄玉玲,王勇.时序电路测试生成新算法研究[J].无线电工程, 2008,38(7):49-52
[9]邵年华,黄领梅,沈冰,等.PSO-SVM模型在蒸发预测中的应用[J].黑龙江水专学报,2009,36(2):8-10
[10]姜明辉,袁绪川,冯玉强.PSO-SVM模型的构建与应用[J].哈尔滨工业大学学报,2009,41(2):169-171
Re s e a rc h of PMV Inde x Fore c a s ting Sys te m ba s e d on PSO-SVM
ZHAO Min-hua1,SU Rui1,XU Li-xian2
1 School of Information and Control Engineering,Xi’an University of Architecture and Technology
2 Automatic Institute of Shandong Academy
With the increasingly widespread application of air-condition,the indoor environmental thermal comfort and the air quality have got more and more people’s attention.Based on this condition,the paper is researched on an adaptive PSO support vector machine classification model given a detailed model of the design steps and implementation code, then the model is validated using the summer PMV data sets of thermal comfort index database on“Intelligent Building Environment Technology Platform”.At last,the experimental results show that the PSO-SVM model is applied to indoor environmental comfort evaluation has certain advantages than the grid-based search-SVM model in depth comparison.
PMV,PSO,support vector machines
1003-0344(2015)03-073-4
2014-1-26
苏蕤(1988~),女,硕士研究生;西安建筑科技大学信息与控制工程学院(710055);E-mail:surui1988surui@163.com
陕西省教育厅自然科学研究项目基金(12JK0999);西安建筑科技大学科技计划项目(JC1215)
