水平突变管内流动形态的数值模拟

邱耀德，罗彬文，彭高

（湖南工业大学 机械工程学院，湖南 株洲 412007）

水平突变管内流动形态的数值模拟

邱耀德，罗彬文，彭高

（湖南工业大学 机械工程学院，湖南 株洲 412007）

为了研究突变管内水流的流动特性，利用计算流体力学软件Fluent，并采用SIMPLEC的求解方法对突变管进行数值模拟。分析不同入口速度、管径比、倾角对再附着长度和局部阻力系数的影响。仿真结果表明：再附着长度与突扩比和倾角有关；突变管的局部阻力系数随着突扩比的增加而增大，且随着倾角的变小而减小；其结果较好地反映了突变管路的基本特征，可为工业生产中常见的此类问题的研究提供参考。

突变管；突扩比；突变管倾角；再附着长度；局部阻力系数

0 引言

突扩管内部流体流动具有惯性，在遇到管道通流截面形状发生变化时，主流束沿着管径逐渐向径向扩大。管壁与主流束之间形成涡旋，涡旋靠主流束带动旋转，致使主流的能量通过粘滞性不断提供给涡旋。同时主流带动涡流不断地通往下游，促使下游一定范围内的紊流脉动变强，加大了这段长度上的水头损失[1]。由于管道通流截面积的突然扩张，导致在面积突然变化的截面后存在回流、分离、再附和剪切等流动现象[2-3]。由于突变管在工业领域内被广泛应用，因此对突变管道内的流动形态进行数值模拟，具有重要的实际意义。

突变管作为各类管网中最基本的连接单元之一，其水力学特性的研究对管网优化起着重要的作用。对突变管水流流动方面的研究，国内已有不少的成果，例如：李栋浩等[4]测定了不同的管道流量、水温以及测压管水头工况下的局部水头损失；分析了局部阻力系数与流速、管径及温度之间的关系；得出了在紊流光滑区，突缩圆管的局部阻力系数与入口速度的对数呈良好的线性关系。孙琳[5]选用4种不同突扩比、3种不同突缩比的模型进行数值模拟和试验研究，得出了圆管突扩、突缩时圆管的局部阻力系数均是入口速度的函数，且突扩圆管的局部阻力系数随着突扩比的增大而减小的结论。有关突变管中再附着长度的影响因素，以及倾角对局部阻力系数的影响的研究文献较少；而再附着点是判断近壁区不再发生回流的重要依据，局部阻力系数是工程中重要的理论参数。因此，本文中利用Fluent软件，对不同的入口速度、管径比和倾角的突变管进行数值模拟分析，探究突变管内流场中再附着长度的影响因素，以及倾角对局部阻力系数的影响。

1 计算模型与网格

1.1 计算模型

由于在入口速度较低的情况下，突扩管中的流场都表现出强烈的二维流动特性，管内流动可看成是轴对称[6]的。为了减少计算量，可将流体在突变管内的流动简化为轴对称流动。突变管的结构简图如图1所示，图中小管直径D1为10 mm，大管直径D2分别取15,20,25 mm，即突扩比E=D2/D1分别取1.5,2.0,2.5三种工况，L1=150D1，L2=50D2，突变倾斜角从90～10°范围内变化。

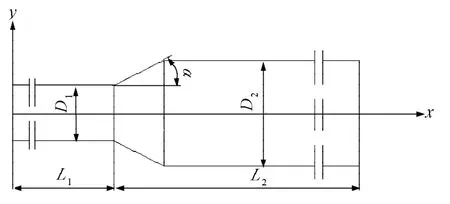
图1 突变管的结构简图Fig. 1The schematic diagram of horizontal mutation pipe

1.2 网格划分

采用GAMBIT软件建立突变管的二维模型，由于轴两侧的流动形态基本相同，因此只模拟上半部分。网格划分采用的方式为Quad（四边形网格），类型为Submap（将一个不规则区域划分为几个规则的区域），边界采取加密处理。以突变倾角取30°的网格图型为例，见图2。

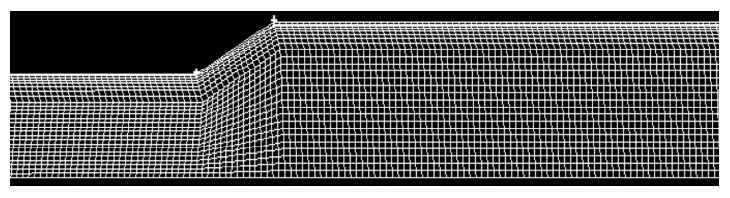
图2 突变管网格模型Fig. 2Mesh model of horizontal mutation pipe

1.3 边界条件及算法

采用速度入口作为入口边界条件，入口速度在0.1～3.0 m/s的范围内变化，此时入口速度相应的雷诺数范围为1 000～30 000。出口采用的边界条件为压力出口，出口压力为标准大气压。壁面采用标准的壁面函数处理。

2 模拟结果与分析

2.1 突扩比对再附着长度的影响

取突扩比E分别为1.5,2.0,2.5，入口速度为1 m/s时的模型进行仿真模拟。经过Tecplot处理之后得到的流线图如图3所示。

图3 不同突扩比下的流线图Fig. 3The streamline diagrams for different pipe expansion ratios

从图3可以看出，当入口速度不变时，随着突扩比的增加，涡旋尺寸也逐渐增大。由于涡旋区压缩主流的过流断面，引起过流断面上近壁面区速度重新分布。所以涡旋尺寸的增大，将导致突变管近壁区速度梯度的建立被推后。而且涡旋区涡旋质点不断耗散的能量都来源于涡旋区与主流的动量交换或粘性传递的补给。因此，涡旋愈大，所需的耗能越多，从主流束中汲取的能量也越多。所以，突扩比的增加会导致能耗的增加。

不同突扩比时，再附着长度随入口速度的变化规律见图4。近壁面区速度对径向求导等于0的地方即为再附着点，突扩截面到再附着点的距离为再附着长度L。图4中是以比值L/H表示再附着长度L的变化情况，其中

从图4可以看出，当突扩比一定时，随着入口速度u的增加，再附着长度也增加，且最终趋于定值。这说明管道通流截面发生变化导致的回流区长度随入口速度的增加而增加，且随着入口速度的增加最后趋于定值。从图4中还可看出，当入口速度一定时，随着突扩比的增加，再附着长度也随之增加。

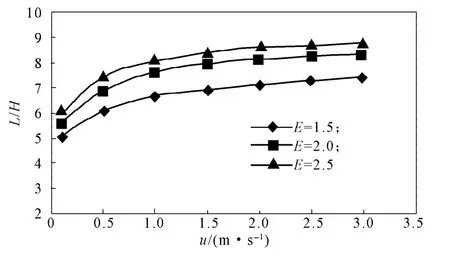
图4 不同突扩比下再附着长度与入口速度的关系Fig.4 The relationship between re-attachment length and the entrance velocity under different expansion ratios

2.2 倾角对再附着长度的影响

取突扩比E为1.5，入口速度为1 m/s，倾角范围为90～10°的计算模型，对其仿真模拟得到的流线图如图5所示。

比较图5中个不同倾角的突变管内流场的流线图可知，突变管的倾角越小，产生的涡旋也越小，且倾角为13°的突变管内流场流线图中几乎看不到涡旋的存在。从图5可看出，由于壁面的挤压，使得原来在壁面拐角与主流束之间形成的涡旋前段被挤压，从而产生的涡旋变小。这主要是由于倾角的变小，导致主流束与边界壁面之间的空间变小，从而使大的涡旋难以产生。

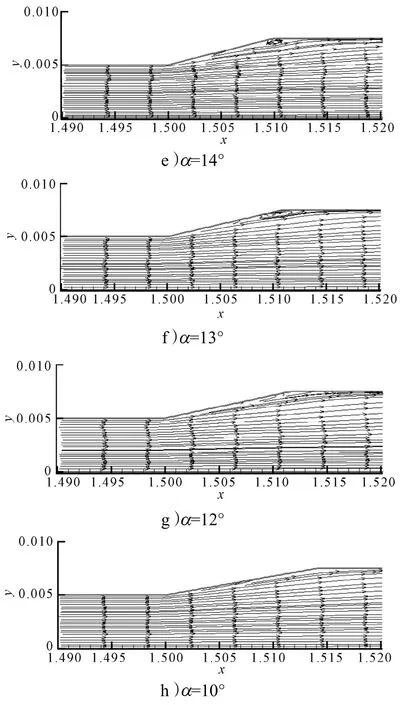
图5 不同倾角下的流线图Fig. 5The streamline diagrams for different inclination angles

入口速度为1 m/s时，再附着长度随突变管倾角变化的规律如图6所示。

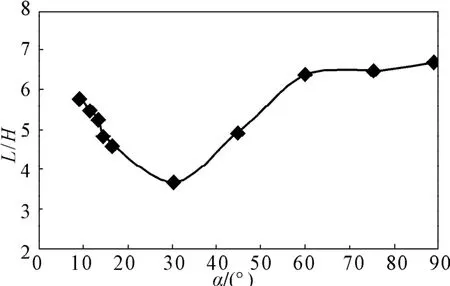
图6 再附着长度与倾角的的关系Fig. 6The relationship between reattachment length and inclination angle

从图6可以看出，突变管内流场中再附着长度在倾角为30°时最小，而在90°时最大。由此可知，突变管内流场中的再附着长度随着倾角的变大先减小后增大。当倾角在10～30°之间变动时，由于倾角过小导致涡旋的产生位置越靠后，使得突变管内流场中的再附着距离变长。故倾角在10～30°之间时，影响突变管内流场中再附着长度的主要因素是倾角。当倾角在30～60°之间变动时，随着倾角的增大，涡旋产生的位置提前，但倾角抑制涡旋的能力也相应减弱，使得涡旋也相应变大。故在倾角为30～60°之间时，影响突变管内流场中再附着长度的主要因素是倾角和涡旋。当倾角在60～90°之间变动时，涡旋的大小基本上不受倾角改变的影响。故在倾角在60～90°之间时，影响突变管内流场中再附着长度的主要因素是涡旋。

2.3 突扩比对局部阻力系数的影响

在工程流体力学中，局部水头损失的一般表达式为

式中：ζ为局部阻力系数；u为管道突变前截断面的平均流速；g为重力加速度。

突扩管的局部阻力系数的表达式为式中A1,A2分别为突扩管截面发生突变前后的管路横断面面积。

按照式（2）计算，得出突扩比E=1.5,2.0,2.5的局部阻力系数分别为0.308 6,0.562 5,0.705 6。

当突扩比E分别为1.5,2.0,2.5时，由模拟计算得到的突扩管局部阻力系数随入口速度的变化规律见图7。

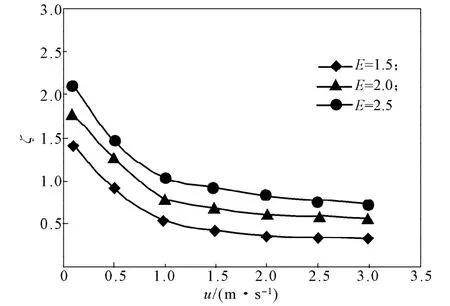
图7 不同突扩比下的局部阻力系数与入口速度的关系Fig. 7The relationship between local resistance coefficient and entrance velocity under different expansion ratios

从图7可以看出，当入口速度较小时，局部阻力系数随着入口速度的增大而减小；但当到达一定的入口速度之后，局部阻力系数趋于定值，此时局部阻力系数只与突扩比有关。在相同的入口速度下，突扩比越大，局部阻力系数也越大。以上2种趋势均是由于入口速度和突扩比的增大，导致更大的涡旋产生，而涡旋的旋转能耗主要是通过主流束的粘滞性不断的供给。在工程流体力学中的局部阻力系数只与突变截面积比有关系，但从图7中可看出，在雷诺数较小时，局部阻力系数随入口速度的变化非常大。这是因为，如果层流经过局部边界几何条件改变的障碍后仍保持层流，流体质点产生剧烈变形，加强了相邻流层间的相对运动，因而加大了这一局部地区的能量损失。

2.4 倾角对局部阻力系数的影响

取突扩比为1.5，入口速度为1 m/s，倾角在 90～10°范围内变化的计算模型，对其仿真模拟，得到突扩比E=1.5时，突变管局部阻力系数随倾角变化的趋势如图8所示。

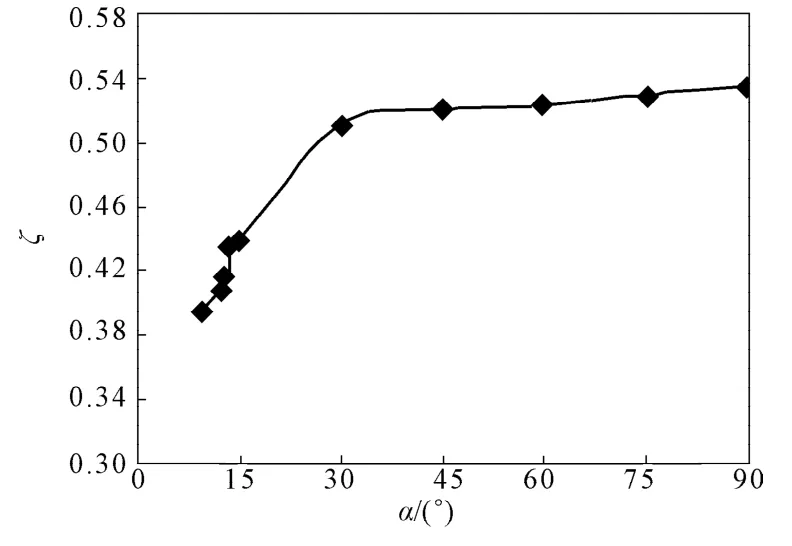
图8 局部阻力系数与倾角的的关系Fig.8 The relationship between local resistance coefficient and inclination angle

从图8可以看出，当突变管倾角越小，局部阻力系数也越小。这是因为突变管倾角越小，抑制涡旋的产生越强，使得主流束的水头损失越少。但局部阻力系数随倾角的变化不是线性的。当倾角在10～30°的范围内变化时，局部阻力系数随倾角的变化较明显。由此可知，当倾角在10～30°的范围内时，突变管抑制剧烈变形而产生的能量耗散比在倾角大于30°时强很多。所以，在工程中应用的突变管倾角最好小于30°，若条件允许，可将倾角做得更小。

3 结论

利用Fluent软件分别对不同入口速度、突扩比和突变倾角的突变管模型进行仿真研究。分析各变量对再附着长度和局部阻力系数的影响。仿真结果表明：

1）再附着的长度取决于突变管道的倾角和流场中的涡旋。

2）突变管的局部阻力系数随着入口速度的增加而减小，最后趋于定值。

3）突变管的局部阻力系数与突扩比和倾角有关。突变管的局部阻力系数随着突扩比的增加而增大，且随着倾角的变小而减小。

[1]周再东，魏长柱，孙明艳，等. 突扩管流动形态的数值模拟[J]. 科学技术与工程，2012，12(30)：185-187. Zhou Zaidong，Wei Changzhu，Sun Mingyan，et al. Sudden Expansion Pipe Flow Pattern of the Numerical Simulation [J]. Science Technology and Engineering，2012，12(30)：185-187.

[2]尹则高，张土乔，黄亚东，等. 连续突扩管流的数值模拟[J]. 流体机械，2005，33(8)：24-27. Yin Zegao，Zhang Tuqiao，Huang Yadong，et al. Numerical Simulation of Serial Sudden Expansions Pipe Flow[J]. Fluid Machinery，2005，33(8)：24-27.

[3]王小华，鞠硕华，朱文芳. 突扩流的数值模拟[J]. 低温建筑技术，2003(1)：59-60. Wang Xiaohua，Ju Shuohua，Zhu Wenfang. Numerical Simulation of Flow at Sudden Expansion[J]. Low Temperature Architecture Technology，2003(1)：59-60.

[4]李栋浩，王文娥，葛茂生，等. 突然缩小圆管局部水头损失系数试验研究[J]. 水力与建筑工程学报，2011， 9(4)：22-24. Li Donghao，Wang Wene，Ge Maosheng，et al. Study on Local Drag Parameter of Subcontract Tube[J]. Journal of Water Resources and Architectural Engineering， 2011，9 (4)：22-24.

[5]孙琳. 圆管突扩（缩）局部阻力试验及流场数值模拟[D]. 哈尔滨：东北农业大学，2010. Sun Lin. Experimental Study and Flow Field Numerical Simulation on Loss of Pipe with Sudden Expansion or Contraction[D]. Harbin：Northeast Agricultural University，2010.

[6]高殿荣，张齐生. 平面突扩管瞬态流动的有限元模拟[J].燕山大学学报，1999，23(4)：331-334. Gao Dianrong，Zhang Qisheng. Finite Element Simulation of Transient Flow in a Planar Sudden Expansion Channel[J]. Journal of Yanshan University，1999，23(4)：331-334.

（责任编辑：邓光辉）

The Numerical Simulation of Flow Pattern in Horizontal Mutation Pipe

Qiu Yaode，Luo Binwen，Peng Gao
（School of Mechanical Engineering，Hunan University of Technology,Zhuzhou Hunan 412007,China）

In order to explore the flow characteristics in horizontal mutation pipe,the SIMPLEC algorithm and the computational fluid dynamics software Fluent are used to make a numerical simulation on the mutation pipe. The effects of different entrance velocity,pipe diameter ratio and inclination angle on the reattachment length and local resistance coefficient are analyzed. The results indicate that the reattachment length is related to expansion ratio and inclination angle; the ocal resistance coefficient increases with the increment of expansion ratio whereas decreases with the decrement of the nclination angle; The results reflect the essential characteristics of mutation pipe flow and provide a reference for solving he common problems in industrial production.

mutation pipe ；expansion ratio ；mutation pipe inclination angle；reattachment length ；local resisance coefficient

TV134

A

1673-9833(2015)01-0048-04

2014-12-19

邱耀德（1989-），男，湖南浏阳人，湖南工业大学硕士生，主要研究方向为高射流理论及其应用，E-mail：943796182@qq.com

10.3969/j.issn.1673-9833.2015.01.009