基于单矢量水听器的Capon空间谱估计

袁永琼++张锴

摘 要：针对复杂海洋环境下的目标方位估计问题，提出了一种基于单矢量水听器数据协方差矩阵的Capon谱估计算法。仿真分析了该算法对窄带信号和宽带信号的方位估计性能。仿真结果表明，在高信噪比下，该算法可以得到目标方位的无偏估计。湖试数据处理结果进一步验证了所提出算法的有效性。

关键词：单矢量水听器；Capon谱估计；数据协方差；无偏估计

中图分类号：TB566 文献标识码：A 文章编号：2095-1302（2015）05-00-03

0 引 言

在海洋信道中，声场的声压和振速是同相位的，这是声压振速信息联合处理的物理基础[1]。传统的单矢量水听器方位估计一般基于声能流的最大似然估计，该技术现已在工程上被广泛应用。同时，也涌现了很多基于单矢量水听器方位估计的新方法和新理论[2]，何希盈提出了一种基于MCDR的单矢量水听器方位估计方法，并推导了该种算法的信噪比分辨门限[3]，王伟提出了一种基于ESPRIT的单矢量水听器方位估计方法，实现了对两个单色信号的多目标分辨等[4]。文献[5]将MUSIC算法用于单矢量水听器方位估计，提高了单个矢量水听器的高分辨方位估计性能。考虑到海洋信道的复杂条件，针对文献[3]提出的基于二维单矢量水听器的MVDR估计器，本文从仿真上分析了该估计器的方位估计性能，并给出了该算法对湖试数据的处理结果。

1 Capon谱估计原理

Capon提出了一种最小方差无失真响应波束形成器[4]，即MVDR（Minimum Variance Distortionless Response） 波束形成器，其准则是在保持观测方向信号功率不变的情况下，使噪声以及来自非信号方向的任何干扰所贡献的功率为最小，因此 Capon 波束形成器可以看成是一个尖锐的空间带通滤波器。

理想情况下，N个窄带远场信号入射至空间M元阵列上，阵列接收的窄带远场信号DOA模型为：

X（t）=A（θ）s（t）+N（t） （1）

其中：X（t）是M×1维快拍数据矢量，A（θ）是M×N维流型矩阵， s（t）是空间信号的N×1维矢量，N（t）是阵列的M×1维噪声数据矢量，在这里：

A（θ）=[a1（θ1）… aN（θN）] （2）

ak（θk）是第k个水声信号的阵列流型，满足：

（3）

则阵列数据的协方差为：

R=E[XH] （4）

则上面的准则可以表示为满足式（5）的条件时波束输出功率（见式（6）所示）最小。

（5）

P（θ）=WHRW（θ） （6）

该最优化问题可采用拉格朗日法求解，代价函数构造为：

H（c）=P（θ）+λ[1-WHa（θ）] （7）

式中：λ为一常数。

将上式对W求微分使其为零，注意到条件式（3），得到MVDR的最佳权为：

（8）

则MVDR输出的角度谱为：

（9）

2 单矢量水听器的Capon空间谱估计

本论文只考虑二维问题，测量方程可表示为：

（10）

式中：P表示矢量水听器输出同点的声压，Vx，Vy表示正交的二维振速，x （t） 是水听器接收的声压波形，θ（-π≤θ<π）为入射声波水平方位角。假设入射到矢量水听器上一个目标信号，通过采样接收三路数据，生成满足式（1）的接收数据模型，一个3×1维的阵列流形a（θ），即：

X（t）=a（θ）x（t）+N（t） （11）

式中： a（θ）是信号在单矢量水听器上的阵列流型，其表达式如下：

（12）

式（12）中，矢量水听器两个振速通道输出第一和第二个分量，是声压信号在X轴，Y轴方向上的投影，矢量水听器声压通道输出最后一个分量。则单矢量水听器的数据协方差矩阵R便可以表示为如式（3）的形式。

现在，我们可以根据式（8）写出单矢量水听器的Capon空间谱输出表达式：

（13）

显然，a（θ）就是上面所说的信号在单矢量水听器上的阵列流型。到此，我们已经将阵处理中“声场方位谱”的概念引入到了单矢量水听器的信号处理中。和传统的Capon谱估计算法一样，本方法也需要在方向轴上进行全域搜索。

特别需要指出的是，基于单矢量水听器的Capon空间谱估计，其阵列流型矢量中各元素分别对应着单矢量水听器、共点接收的声压和振速，仅包含目标的方位信息，而无时间延迟信息，与到达信号的频率无关，因而不会出现传统方位估计中的频率模糊问题。该流型矢量始终满足前两个分量范数且与最后一个分量相等，等于1[4]。

3 仿真分析

3.1 窄带信号的方位估计

本文仅考虑单目标的情况。仿真中参数设置为：噪声模型为1 kHz零均值高斯噪声，信号参数为θ=30°，f =500 Hz的单频信号，样本点数1 000，搜索步长Δθ=0.1°，采样频率4 kHz，统计100次独立实验的数据结果。

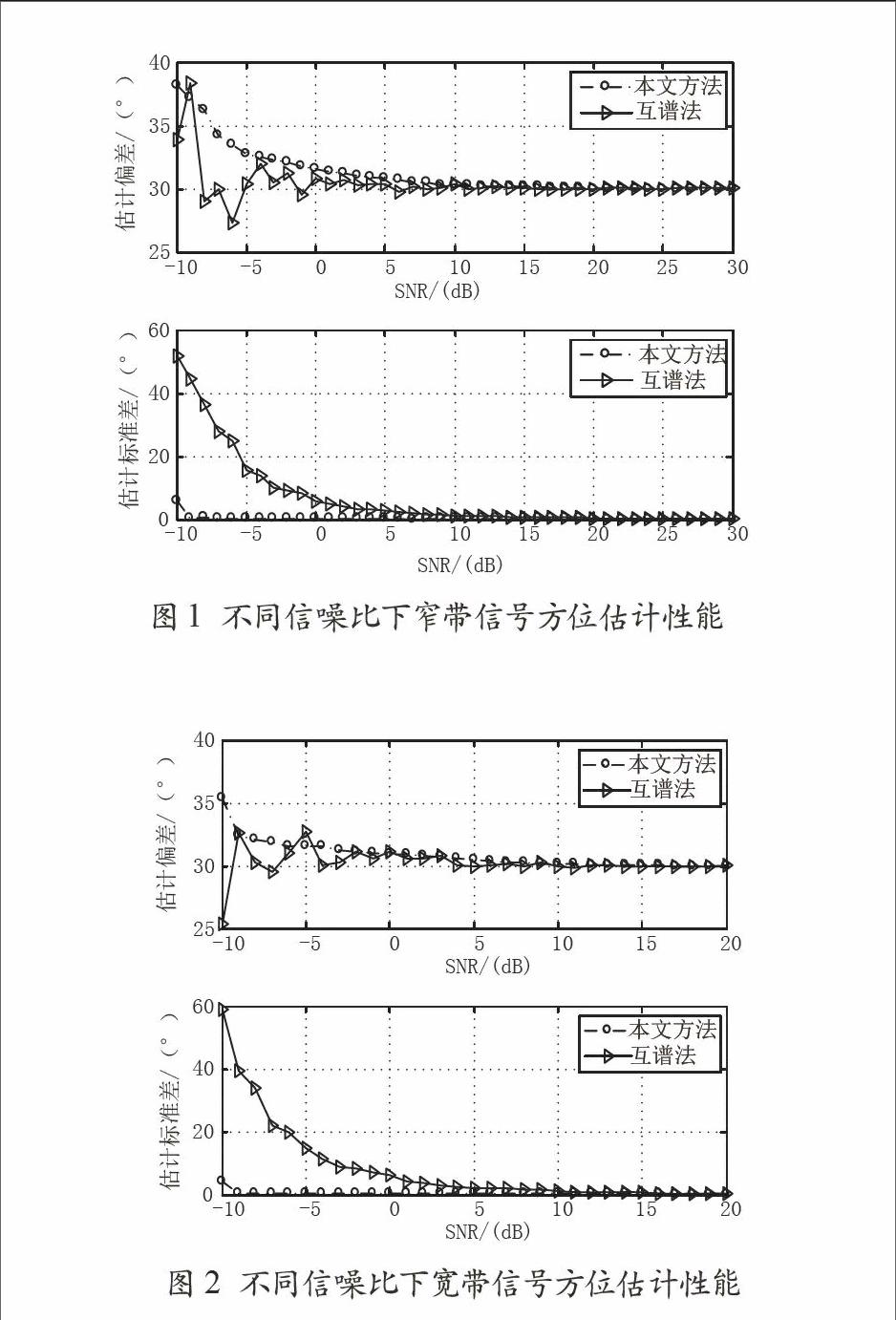
图1给出了不同信噪比下窄带信号方位估计性能曲线，并与基于声能流的复声强器方位估计的结果进行对比。从图1可看出，两种方法的方位估计偏差在10 dB附近都在1°以内。注意到，在低信噪比情况下，互谱法的方位估计在真实值附近上下波动[7]，而本文方法的方位估计是有偏的。这是因为：信号方向决定于接收数据矩阵协方差矩阵R的对角线上能量之比，由于各个通道接收的噪声功率相同，随着信噪比的降低，对角线上噪声所占的比重逐渐增加而使对角线上能量趋于相等，所以方位估计结果有接近45°的趋势。

观察还发现，在10 dB附近本文方法和互谱法的估计标准差都在1°之内，随着信噪比的降低，互谱法方位估计精度出现下降，而本文算法标准差依然很小，这是低信噪比条件下两种算法估计方位分布趋势的不同。值得注意的是，论文所提出方法的方位估计标准差与搜索步长相关。若搜索步长较大，即使方位估计标准差很小，也是有偏估计。当在足够信噪比条件下，搜索步长越小，方位估计精度越高，可达到无偏估计。

图1 不同信噪比下窄带信号方位估计性能

3.2 宽带信号的方位估计

仿真参数设置：带宽1 kHz零均值高斯噪声，信号参数θ=30°，1 kHz 的宽带信号，样本点数1 000，搜索步长Δθ=0.1°，采样频率4 kHz，统计100次独立实验的数据结果。

图2给出了不同信噪比条件下宽带信号的方位估计性能曲线，并与互谱法的方位估计结果进行对比。从图2可看出，与窄带信号类似，两种方法在10 dB附近的方位估计偏差均在1°以内，并且互谱法的方位估计在真实值附近上下波动[5]，而论文提出的方法方位估计是有偏的。但在足够的信噪比条件下，搜索步长越小，本文算法的宽带信号方位估计精度越高，也可达到无偏估计。

图2 不同信噪比下宽带信号方位估计性能

4 湖试数据

实验中目标信号为宽带高斯噪声，所占频带500～5500Hz，采样频率16 kHz，当发射信号时接收信噪比很高，可近似看作纯目标信号，而不发射信号时采集的数据为纯干扰数据。

图3给出了某一时刻湖试数据处理得到的方位谱曲线。为了便于对比，给出了同一段数据的互谱直方图[8]。从图3中可看出，该算法比直方图具有更好的方位分辨能力。同时对方位估计结果也进行了比较，基于声能流的方位估计得到的结果是133.206 9°，而该算法的方位估计得到的结果是134.3°，结果验证了算法的有效性。注意到本文算法的估计精度低于传统方法，这是因为采用搜索步长Δθ=0.1°的结果。在实际应用中，可采用先进行目标方位粗测，确定目标的大致方位后再进行细测的手段来提高方位估计的精度。图4显示出了两种算法对20 s湖试数据处理得到的方位瀑布图，由图中可以看出该算法清晰的给出了目标的方位历程。

图3 方位谱比较图

图4 湖试结果的瀑布图

5 结 语

针对复杂海洋环境下的目标方位估计问题，提出了一种基于单矢量水听器的Capon谱估计算法。结合水听器自身的阵列流型特点，将Capon波束形成器算法应用到单矢量水听器上实现方位估计。仿真结果表明，在足够的信噪比和搜索步长下，该算法可以得到渐进无偏估计，湖试数据进一步验证了算法的有效性。

参考文献

[1]惠俊英，慧娟.矢量信号处理基础[M].北京：国防工业出版社，2009.

[2]张锴. 基于声矢量传感器的空间谱估计算法研究[D]. 哈尔滨：哈尔滨工程大学， 2012.

[3]何希盈， 程锦房，邓大新，等.单矢量水听器的MVDR波束形成性能研究[J].兵工自动化，2009，28（11）：59-61.

[4]王伟. ESPRIT方法在矢量水听器多目标方位估计中的应用[J].声学与电子工程，2006（3）：19-23.

[5]徐海东，梁国龙，惠俊英.解析声能流Capon空间谱估计[J]. 声学技术，2004，23（3）： 178-192.

[6]梁国龙，张锴，付进，等. 单矢量水听器的高分辨方位估计应用研究[J].兵工学报，2011， 32（8）：986-990.

[7]王德俊.矢量声场与矢量信号处理理论研究[D].哈尔滨：哈尔滨工程大学，2004.

[8]姚直象，惠俊英，殷敬伟，等.基于单矢量水听器的四种方位估计方法[J].海洋工程，2006，24（1）：122-127.