基于复杂网络视角的农产品价格波动和机理分析

高齐圣, 路 兰

(青岛大学经济学院，山东 青岛 266071)

基于复杂网络视角的农产品价格波动和机理分析

高齐圣, 路 兰

(青岛大学经济学院，山东 青岛 266071)

为深入研究中国农产品价格波动和传导机制，选择籼稻、粳稻、小麦、玉米和大豆等5种大宗农产品为代表，借助符号动力学方法建立了农产品价格同步传导复杂网络模型。研究了该网络波动幅度和强度分布、聚集系数、强度与聚集系数相关性等网络拓扑性质，并以中国1997年4月到2012年12月期间相关价格数据进行了实证分析。最后提出了新形势下中国农产品价格调控的对策及建议。

大宗农产品；价格传导；复杂网络；符号动力学；对策建议

0 引言

中国加入WTO已经12年多，国际市场对中国农产品供求和价格波动的影响，正在显著增强[1]。国际市场农产品价格影响因素的复杂化和多样化，很容易传导到国内，导致国内农产品市场复杂多变[2]。农产品价格一直是近年来大众关注的焦点。2007年中国许多产品由于原料短缺造成了涨价，如猪肉、粮食、禽蛋奶等农产品价格的上涨，其中大宗农产品价格上涨与减产、成本提高等因素有关，价格上涨问题已经引起了国家的高度重视。中国是世界上最大的农产品消费国，也是全球范围内农产品的主要产地之一。农产品价格不仅事关城市居民的生活质量，而且直接决定着农村居民的收入水平。因此，大宗农产品价格调控是中国政府的重要职责，具有特殊的政治和经济意义。

大宗农产品的价格合理、稳定有利于整个社会的稳定和市场经济的发展。至今，关于大宗农产品价格的文献已有很多，他们讨论的问题大致可以归结为：从国内、国际市场、国际农产品价格以及金融属性等方面对大宗产品价格的影响因素进行了分析和讨论[2-4]；利用技术商品的理论价格模型或是经济批量的数学折扣定价模型研究大宗农产品定价问题,尤其是上个世纪90年代兴起的复杂网络理论为价格波动的研究提供了一种新的思路[5-6]。苑莹等[7]采用符号序列化的方法对股票价格指数进行了预测研究。此外，符号动力学是一种简单的动力学系统，它由符号序列构成，是现实复杂动力系统的抽象和粗粒化描述[8]。刘向荣等[9]借助符号动力学方法建立了中国工业产品价格同步传导复杂网络，为开展价格预测与调控提供了新视角和途径。徐梅[10]等采用符号时间序列分析方法从大尺度的角度分析收益变化的特征，提出了确定收益变化的主要模式并预测收益水平的方法。宋爱玲等[11]采用符号动力学的方法分析心率变异性，并给出了相关参数选择的标准。然而，利用复杂网络以及符号动力学方法对大宗农产品价格波动分析的文献[12]还不多见。

农产品包括食品和农业原料，本文选取分类食品中籼稻、粳稻、小麦、玉米和大豆等，借助复杂网络以及符号动力学方法对大宗农产品价格波动模型进行分析，通过对强度分布、聚集系数以及相关性等指标进行分析，给出了对大宗农产品价格上浮、保价以及价格下调时的宏观调控策略建议，这些建议可以使政府对大宗农产品定价调控政策更加合理科学。

1 构造价格同步传导演化复杂网络

1.1 价格数据的符号化过程

时间序列符号化的基本思想是将原始时间序列(或由原始时间序列转换得到的序列，如连续时间点间的一阶差分序列)划分为有限个数的区间，每个区间分配不同的符号，每个原始数据根据落入区间的不同对应不同的符号。如果原序列{xt,t=0,…,N-1}中不同时间点的数据值落入同一个区间，则被转换为同一符号，这些符号标记了序列所属的区间，描述了序列的动态特征。当原始序列非平稳或原始数据随时间的变化比其绝对数值更重要时，通常针对原始序列的一阶或高阶差分序列进行符号化，称为动态符号化方法。可采用序列样本的均值或中值等作为不同符号之间的划分，数据符号化是一个“粗粒化”的过程，即只捕获大尺度的特征，从而降低噪声对统计算法的影响。一旦原始时间序列转化为符号序列后，就要提取符号序列的特征量对其进行定量分析。

根据上述思想，本文考察了大宗系列农作物从1997年4月到2012年12月的价格波动情况。其中大宗系列农作物包括籼稻、粳稻、小麦、玉米和大豆，分别将这5种农作物的价格波动采用Parkinson的价格波动幅度的定义进行分析。价格波动幅度[8]的定义为

FDt=lnht-lnlt

将价格波动幅度定义为一段时期内最高价对数与最低价对数之差。其中，FDt、ht和lt分别代表第t个时间段内价格波动幅度、最高价及最低价。

以大宗农产品籼稻、粳稻、小麦、玉米和大豆月度价格为单位，步长为1个月做数据滑动，计算价格波动幅度，得到5组时间序列数据，每组的数据个数均为188个。

为研究上述5种价格数列同步变动情况，按照如下方法将其转变为符号时间序列，以籼稻价格数列为例：

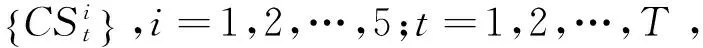
1.2 价格同步传导符号复杂网络的构建

农产品价格的波动都具有一定的关联性，为此仿效三月移动平均线做法，以3个变动率符号作为一个符号序列，称为模态。按照价格时间序列转化为符号时间序列可知，理论上最多应有27(33)种不同模态。以此不同模态作为网络节点，并给予编号，按照时间顺序从1997年4月到2012年12月，每个月对应27个模态中的某个模态，将本月至下月转换的两个模态用边相连。通过对时间序列波动幅度的粗粒化处理，可将其波动幅度变动关系转换为不同的模态来表示，后一个模态的形成以前一个模态为基础，模态之间相互转换，由此形成了一个复杂网络系统，注意这里不考虑自环的情况，即如果相邻的两个模态相同，则将不做任何处理，由此可构建时间序列波动幅度的复杂网络模型。模型中，以不同的波动序列模态为节点，序列模态相邻就代表两个序列模态之间有连边，表示模态之间的转换，如果任意的两个模态之间存在多次转换，就将转换次数定义为边权值。根据上述思想，就构造了一个加权无向的复杂网络模型。

籼稻、粳稻、小麦、玉米和大豆构造出的加权无向复杂网络如图1所示。

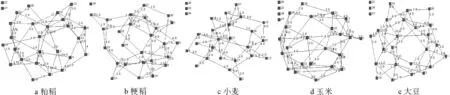
图1 5种农产品价格传导的网络结构图

2 农产品价格波动与传导机制分析

2.1 波动幅度模态强度分析

波动幅度模态统计规律是对波动幅度模态间复杂关系的刻画。首先对籼稻、粳稻、小麦、玉米和大豆价格单个波动模态的抽象符号序列进行考察。频率体现的是该抽象符号在整个符号时间序列中出现的比例，代表了农产品价格波动的长期趋势。统计结果如表1所示。

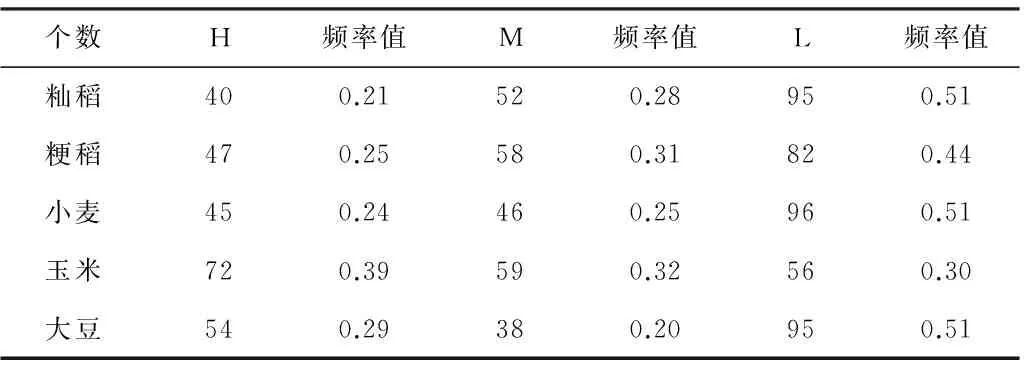
表1 单个符号序列度值统计表

通过对大宗系列农作物价格波动幅度单符号序列模态进行统计计算，发现对于籼稻、粳稻、小麦和大豆这4种农作物，代表波幅较小或无波幅的符号L所占比重依次为51%，44%，51%，51%。这说明在1997年到2012年年底这16年期间，籼稻、粳稻、小麦和大豆价格呈上涨趋势，但波动幅度相对较小。而对于玉米，代表波动幅度较大的符号H所占比重达39%，比其他两种情况都要高，说明这16年期间，玉米的价格波动上涨幅度较大，这反映出了农产品价格波动的品种差异性。究其原因，政府政策是玉米价格波动的主要外因，其与政府主导的粮价政策关系密切。2009年中国进口玉米的量达到了1.294×109kg，较前一年的4.7×107kg有了大幅度的提升，进口量的增加必然会导致玉米价格的提升。从价格波动符号序列也可以发现，从2009年5月份开始，玉米价格一路上扬。

对构建的复杂网络模型进行模态顶点强度分析。对于波动幅度序列模态，不仅要考虑模态出现的频率，还要考虑不同模态间的作用强度，它度量了农产品价格波动各个模态之间的短程相关程度。为此，采用模态顶点强度来进行统计分析。模态顶点强度的定义为

其中，Ni为与顶点i相连接的由顶点i指向的所有近邻顶点的集合,wij为顶点i到j的权重。顶点强度越大，表明该模态与其它模态关联性越强，向其它模态转化的次数越多，在模态之间转换中的地位越重要。按照顶点强度的定义对不同的模态进行分析，得到的结果如表2所示。

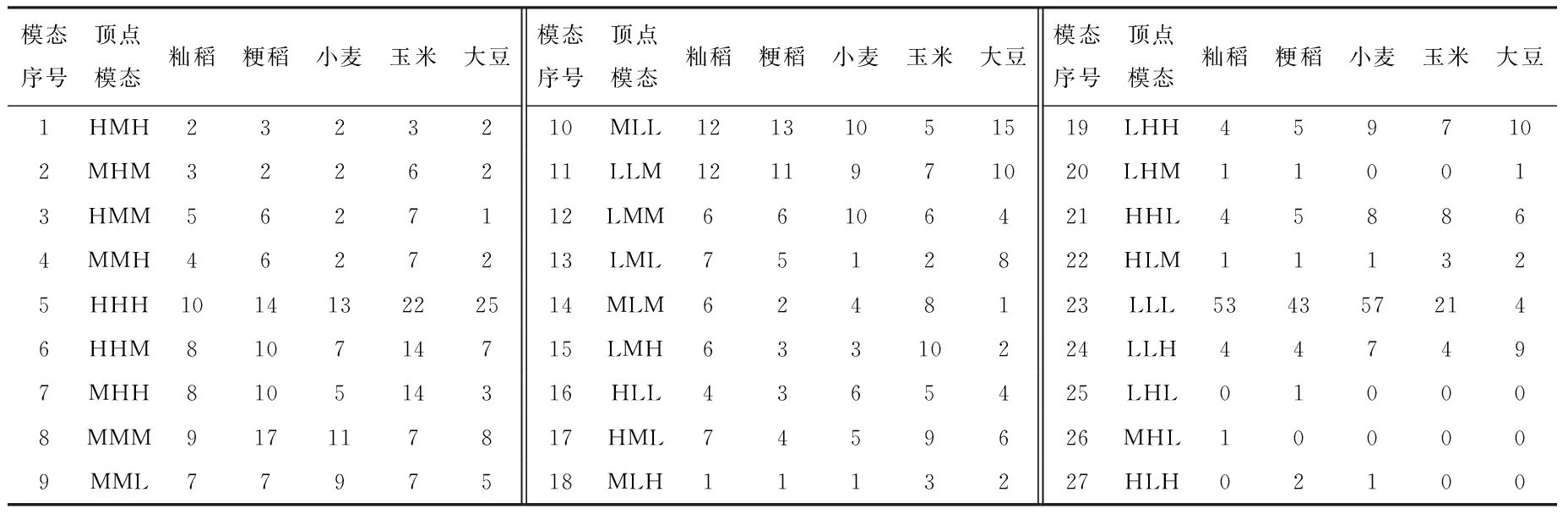
表2 波动幅度序列模态强度统计表

由表2可知，在籼稻、粳稻和小麦的波动幅度序列中，模态LLL顶点强度最大，强度分别为53、43、57。表明在籼稻、粳稻和小麦价格波动过程中，连续3个月小幅上涨的模式占主导地位。在大豆的波动幅度序列中，模态HHH顶点强度最大，强度为25。表明在大豆价格波动过程中，连续3个月大幅上涨的模式占主导地位。而对于玉米的波动幅度序列中，出现了两个强度较大的模态HHH和LLL,强度分别为22和21。连续3个月大幅上涨和小幅上涨的交替出现，反映出中国从国外大量进口玉米政策实施后对价格波动的传导机制和影响结果。至于在大豆和玉米价格波动过程中，模态HHH定点都表现出强度最大，表明在5种大宗农产品价格波动中，大豆和玉米上行压力巨大。

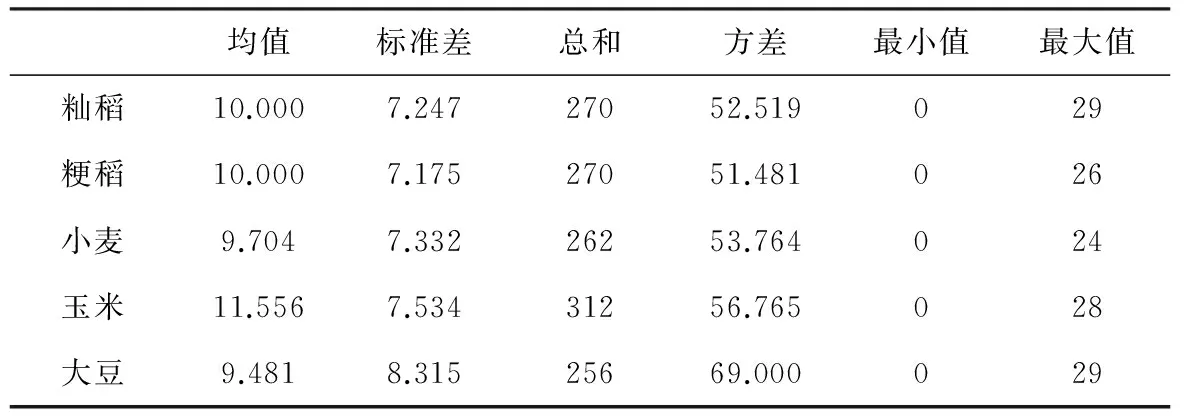
表3 各波动幅度序列模态的节点强度比较分析

从表3中可知，大宗系列的农作物价格波动幅度序列模态的节点强度的均值、方差大致相同。这说明从1997年到2012年年底这16年间，籼稻、粳稻、小麦、玉米和大豆的价格波动仍处在稳定状态。

2.2 波动幅度序列模态强度分布分析

在复杂网络中，顶点度定义为与该顶点连接的其它节点之间的边的数目。网络顶点度分布定义为

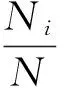
其中，Ni代表度值为k的节点数，N为顶点(即不同模态)总数目。顶点度分布反映了价格波动各模态之间的短程相关程度。强度分布是在加权网络中的度分布，与度分布不同的一点是，考虑了顶点边权值。权重表示两个顶点之间关系的紧密程度，权重越大，关系越紧密。对网络顶点强度分布类型进行如下负幂律假设检验：

H0:p(k)=αk-β

分别对籼稻、粳稻、小麦、玉米和大豆4种复杂网络，做出顶点强度分布的双对数曲线统计分析，如图2所示。

图2 节点强度分布图Fig.2 The distribution of strength of vertex

图2中给出了籼稻、粳稻、小麦、玉米和大豆的价格波动幅度序列模态节点强度分布双对数曲线图。从图2可以发现，籼稻、粳稻、小麦和大豆的价格波动幅度序列模态的分布大致相同，呈现出一定的负幂律性质。负幂律性质表明顶点强度服从Pareto分布，即服从80/20原则。少数的模态顶点具有很大的影响力，决定了整个农产品价格的长期走势，与其它大部分的模态顶点都有一定的短程相关性。如籼稻、粳稻和小麦的价格稳定中，模态LLL起到了关键少数的作用，而大豆的价格稳定中，模态HHH起到了关键少数的作用。另外，由于中国从国外大量进口玉米政策实施后对价格波动产生了很大的影响，玉米的价格波动幅度序列模态的分布较不规律，并没有呈现负幂律特征。

2.3 聚集系数的统计分析

聚集系数作为网络的另一个重要参数，它衡量的是网络集团化程度，即网络顶点主体间的熟悉程度。借助这一指标来研究大宗系列农产品价格波动的周期性规律。无权网络中所有的边都可看作是同质的，但现实中的网络基本上都是加权网络，而且连接顶点的边所蕴含的能力和强度都是异质的。加权聚集系数是有向复杂网络中表示网络顶点近邻之间聚集性质的一个统计参数，加权聚集系数值越高，代表该模态反复出现在谷值点和峰值点，该模态与其他模态转换越频繁越紧密，价格波动周期越短。籼稻、粳稻、小麦、玉米和大豆价波动幅度复杂网络均属于加权复杂网络，加权聚集系数定义为

其中，Wij为顶点(i,j)边的权重，ki为顶点i的强度，si为顶点i的度数。aijajkaki代表3个节点之间是否相互有关联，值为0表示它们之间没有关联，值为1表示它们之间有边相关联，如果三者之间均有关联，表示它们构成一个三角形。加权聚集系数值越高，代表该模态在网络中位置越重要，该模态与其他模态转换越频繁越紧密。

图3中为5种农作物价格波动幅度序列模态的聚集系数的变化图。从图3可以看出，除了玉米，籼稻、粳稻、小麦和大豆的聚集系数序列的波动周期以及变化规律基本相同。而从玉米的聚集系数序列的波动中明显可以看出，从模态MML开始聚集系数基本上为0，说明玉米价格的时间序列波动周期性最长，反映出进口政策对其抑制波动周期的影响。综合分析占有重要地位的模态主要有5种，这5种模态决定了玉米，籼稻、粳稻、小麦和大豆等大宗农产品价格的周期性波动。

表4中给出了这5种农作物的价格波动幅度序列模态的聚集系数排名前5位的序列模态。进一步分析发现，在所有27种模态中聚集系数排名前5位的只出现了14种，许多模态并未出现。并且在这14种序列模态中，其中HHH、MMM、HMH以及LML这4种序列模态出现的频率相对较大。说明这4种序列模态在网络中的位置很重要，该模态与其他模态转换比较紧密。这4种序列模态在复杂网络中的地位一旦发生变化，不仅会强烈影响到其周边的序列模态，也会波及到整个价格波动序列的周期性结构。依据市场定价原则，重新估计农产品的价格，当农产品的市场价格处于较低水平时(如处在LML序列模态)，应对生产者进行补贴；当农产品的市场价格处于高水平时(如处在HHH、MMM和HMH序列模态)，对消费者给予适当补贴，始终保持其市场价格的平稳，尽量避免农产品价格的大起大落。

2.4 强度与聚集系数的相关性分析

价格波动符号序列网络中，节点强度衡量的是价格波动序列模态在整个价格波动序列中影响的强度，而聚集系数衡量的是在以其为核心的局部小范围内的关联紧密程度，聚集系数是综合了节点强度中的边权值，所以影响力较强的序列模态在其周边局部也会得到体现。图4中给出了籼稻、粳稻、小麦、玉米和大豆这5种农作物的节点强度序列与聚集系数系列的关系图。从图中可以发现节点强度与节点聚集系数大致呈正比关系，即节点的强度越大则其聚集系数也越大，这与上述的分析是完全相符的。

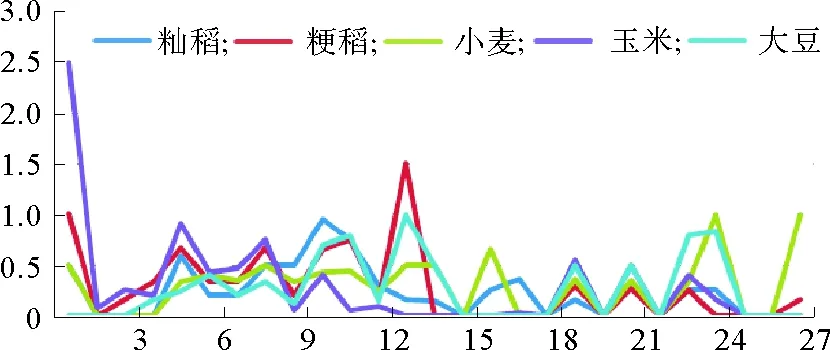
图3 价格波动幅度序列模态的聚集系数变化图

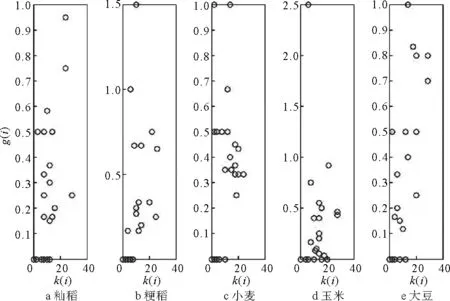
图4 强度与聚集系数的相关性分析

3 结论与建议

文中主要从网络的视角对大宗系列农作物(籼稻、粳稻、小麦、玉米和大豆)的价格波动情况进行了分析和对比。将籼稻、粳稻、小麦、玉米和大豆的价格波动进行符号化，构建了时间序列波动幅度的加权网络模型，通过对该模型的强度、强度分布、聚集系数以及相关系数等相关指标进行分析，最后得到结论：1)通过对大宗系列农作物价格波动幅度单符号序列模态进行统计计算，在1997年到2012年年底这16年期间，籼稻、粳稻、小麦和大豆价格波动幅度变动较稳定。而对于玉米来说，代表波动幅度较大的符号H所占比重达39%，比其他两种情况都要高，说明这16年期间，玉米的价格波动幅度相对比较大。通过分析籼稻、粳稻、小麦、玉米和大豆的价格波动幅度序列模态节点强度分布，发现籼稻、粳稻、小麦和大豆的价格波动幅度序列模态的分布大致相同，具有一定的幂律性质。但玉米的价格波动幅度序列模态的分布较不规律，并没有呈现出线性关系。农作物的价格在很大程度上受国家政策的影响，2009年后中国大大提高了玉米的进口量，这势必会导致国内玉米价格大幅上涨，国家应该充分发挥国家支农惠农政策的作用，减免农业税，保护好农民利益，维持农业生产资料价格的稳定，降低农业生产成本。总之，采取各种积极有效的措施维持农产品价格稳定，减少农产品价格的上涨频率。2) 通过对籼稻、粳稻、小麦、玉米和大豆的价格波动幅度序列模态聚集系数分析，发现HHH、MMM、HMH以及LML这4种序列模态在网络中的位置很重要，该模态与其他模态转换比较紧密。如果大宗系列农作物价格波动序列中发现了HHH、MMM、HMH以及LML这4种序列模态，则应该依据市场定价原则，重新估计农产品的价格。当农产品的市场价格处于较低水平时，对生产者进行补贴；当农产品的市场价格处于高水平时，对消费者给予适当补贴，始终保持其市场价格的平稳，尽量避免农产品价格的大起大落。3)通过对强度与聚集系数的相关性分析得到，籼稻、粳稻、小麦、玉米和大豆这5种农作物的节点强度序列与聚集系数系列呈正比关系，即节点的强度越大则其聚集系数也越大。对农产品价格的调控，应特别关注那些价格波动幅度较大的农产品，当价格波动连续出现上涨或是下降，且出现的频率比较高，则应充分发挥政府的市场调控作用，对价格进行调整，通过降低连续波动模态的聚集能力，达到政府对市场波动的调控能力，预防农产品价格的暴涨暴跌。

[1]农业部农村经济研究中心课题组.农产品价格波动、机理分析与市场调控[J].农业技术经济，2012，(10):4-13. The team of rural economy research center in ministry of agriculture. The price fluctuation of agricultural products, mechanism analysis and market regulation[J]. Journal of Agrotechnical Economics, 2012，(10):4-13.

[2]王少芬,赵昕东.国际农产品价格波动对国内农产品价格的影响分析[J].宏观经济研究，2012，(9):81-86. Wang Shaofen, Zhao Xindong. The impact analysis of international agricultural product price fluctuation on the domestic volatility[J]. Macroeconomics, 2012，(9):81-86.

[3]罗锋.外部冲击对我国农产品价格波动的影响分析--基于SVAR模型研究[J].农业技术经济,2011，(10):4-11. LuoFeng. The impact analysis of Outside Shock on the domestic agricultural product price volatility-based on the study of SVAR[J]. Journal of Agrotechnical Economics, 2011，(10):4-11.

[4]胡冰川,徐枫,董晓霞.国际农产品价格波动因素分析-基于时间序列的经济计量模型[J].中国农村经济,2009，(7):86-95. Hu Bingchuan,XuFeng,DongXiaoxia. The factor analysis of international agricultural price volatility-based on econometric model of time series[J]. Chinese Rural Economy,2009，(7):86-95.

[5]陈卫华，徐华，郭琦.国际石油价格复杂网络的动力学拓扑性质[J].物理学报，2010,59(7):4514-4523. Chen Weihua, XuHua, Guo Qi. Dynamic analysis on the topological properties of the complex network of international oil prices[J].ActaPhysicaSinica, 2010,59(7):4514-4523.

[6]周磊,龚志强,支蓉等．利用复杂网络研究中国温度序列的拓扑性质[J]．物理学报，2008，57(11): 7380-7389． Zhou Lei, Gong Zhiqiang, ZhiRong, et al. An approach to research the topology of Chinese temperature sequence based on complex network [J]. ActaPhysicaSinica, 2008, 57(11):7380-7389.

[7]苑莹,庄新田．基于符号序列方法的股价指数预测研究[J]．数理统计与管理，2007，26(4): 602-609． Yuan Ying, ZhuangXintian. The forecasting research of stock price index by the symbol sequence[J]. Application of Statistics and Management, 2007,26(4):602-609.

[8] Brida, J.G., Punzo,L.F. Symbolic time series analysis and dynamic regimes[J]. Structural Change and Economic Dynamics，2003,14(2):159-183.

[9]刘向荣,杨建梅,孙红英，等.基于符号动力学的中国工业产品价格传导复杂网络分析[J].工业工程,2013,16(4):49-72. Liu Xiangrong, Yang Jianmei, Sun Hongying, et al. A study on complex networks for price transmission of industrial products in china based on symbolic dynamics[J]. Industrial Engineering Journal, 2013,16(4):49-72.

[10]徐梅,黄超．基于符号时间序列方法的金融收益分析与预测[J]．中国管理科学，2011，19(5): 1-9． Xu Mei, Huang Chao. Analysis and forecasting of financial returns based on symbolic time series method [J]. Chinese Journal of Management Science, 2011,19(5):1-9.

[11]宋爱玲,黄晓林,司俊峰等.符号动力学在心率变异性分析中的参数选择[J].物理学报.2011,60(2):020509. Song Ailing, Huang Xiaolin, Si Junfeng, et al. Optimum parameters setting in symbolic dynamics of heart rate variability analysis[J]. ActaPhysicaSinica, 2011, 60(2):020509.

[12]顾国达，方晨靓.农产品价格波动的国内传导路径及其非对称性研究[J].农业技术经济，2011，(3):12-20. GuGuoda, Fang Chenliang. Domestic transmission path for fluctuations in prices of agricultural products and its non-symmetry characteristics[J]. Journal of Agrotechnical Economics, 2011，(3):12-20.

(责任编辑 耿金花)

Agricultural Price Volatility and Mechanism Analysis Based on Complex Networks

GAO Qisheng, LU Lan

(School of Economic, Qingdao University, Qingdao 266071, China)

In order to further research on agricultural price volatility and the transmission in our country, an agricultural prices synchronous transmission complex network model is built based on the method of symbolic dynamics, which Nonglutinous rice, Japonica rice, Wheat, Maize and Soybean are selected as 5 kinds of commodities in bulk farm-products. Network fluctuation, strength distribution, cluster coefficient and the dependency between strength and cluster coefficient are studied in our paper. And empirical analysis is given based on price data during April 1997 to December 2012 in our country. At last, countermeasures and suggestions about price adjustment and control in our country are proposed.

bulk farm-products; price transmission; complex networks; symbolic dynamics; countermeasures and suggestions

1672-3813(2015)04-0090-07;

10.13306/j.1672-3813.2015.04.013

2015-01-27 ；

2015-04-21

教育部人文社会科学研究规划基金(11YJA630019)

高齐圣(1966-)，男，山东潍坊人，博士，教授，主要研究方向为系统工程与质量管理。

N949

A