一种新的数据流模糊聚类方法
2015-07-18孙力娟陈小东
孙力娟 陈小东 韩 崇 郭 剑
①(南京邮电大学计算机学院 南京 210003)
②(南京邮电大学江苏省无线传感网高技术研究重点实验室 南京 210003)
一种新的数据流模糊聚类方法
孙力娟*①②陈小东①韩 崇①郭 剑①②
①(南京邮电大学计算机学院 南京 210003)
②(南京邮电大学江苏省无线传感网高技术研究重点实验室 南京 210003)
针对数据流上的聚类任务受到时间、空间限制等问题,该文提出一种基于权值衰减的数据流模糊微簇聚类算法(WDSMC)。该算法使用改进的带权值的模糊C均值算法进行处理,并采用微簇结构和权值时间衰减结构提高聚类质量。实验表明,相对于现有的数据流加权模糊 C均值聚类(SWFCM)算法和 StreamKM++算法而言,WDSMC算法具有更好的聚类精度。
数据挖掘;数据流;模糊C均值聚类;权值衰减;微簇聚类
1 引言
随着计算机、通信技术的发展以及大数据的到来,在如传感器网络、气象分析、股票市场、计算机网络入侵检测等众多应用领域产生了一些海量、高速、动态到达的数据,这些连续到达的数据被称之为数据流。传统的数据挖掘一般是建立在数据集是有限的,由静态概率分布产生并能够在内存随机存取的基础之上。但是对于数据流而言,传统处理静态数据集上的挖掘算法受到如下条件限制[1]:(1)数据对象是连续不断到达的;(2)无法控制数据对象的处理顺序;(3)数据流的大小是没有边界的;(4)数据对象被处理完后就会被丢弃。在实际处理时,可以使用备忘机制将部分数据保存一段时间后再丢弃;(5)数据可能是动态分布的而非单一的静态分布。聚类分析在数据挖掘领域中扮演一个重要的角色。聚类是一个把数据对象划分成多个组或簇的过程,使得簇内的对象具有很高的相似性,但与其他簇中的对象很不相似[2]。
文献[3]中提出的Brich算法是最早提出的可以用于数据流的聚类算法,选择正确的参数对 Brich算法实现效率很重要,需要专业领域的知识。文献[4]提出一种称为Clustream的数据流聚类算法。它将整个聚类过程分成了两个部分:在线部分和离线部分。在线部分通过设定好的删除和合并原则增量更新微簇的特征向量。离线部分使用改进的 K-means算法将微簇聚类成最终的簇,通过倾斜的时间窗口可以在用户指定的不同时间粒度内发现簇。文献[5]和文献[6]所提出基于密度的数据流聚类算法,能够得到任意形状的簇结构,但不能随着数据流的变化而动态改变,也无法在多种层次粒度下对数据流进行聚类。文献[7]提出的StreamKM++算法是一种使用树结构和桶结构的数据流聚类方法。该算法将数据点不断放入桶中,当两个桶满时,通过调用 Coreset树将桶合并,以此类推,最后将得到的数据点使用kmean++[8]算法合并成簇中心。
上述文献中的算法都属于是硬聚类算法,即每一个数据点不是完全属于这一个簇,就完全属于另一个簇。这种算法不具有一般意义,因为在模糊逻辑的思想中,一个数据点可能同时是许多簇的成员。文献[9]提出的模糊C均值(Fuzzy C-Means,FCM)算法是数据集上的模糊聚类算法,通过不断迭代计算簇中心和隶属度矩阵,求解目标函数的最小值。数据流权值模糊 C均值[10](Stream Weight Fuzzy C-Means,SWFCM)算法将FCM扩展到数据流上,由于该算法每部分仅保留簇中心点及其权值,相对于原始数据信息丢失量过大,聚类的效果并不是十分理想。针对数据流在不同时间段可能形成不同聚类模式的问题,文献[11~13]提出了在数据流处理过程中可能出现的概念漂移检测和处理方法。文献[14]使用一种延迟处理的方法解决数据流聚类中的孤立点检测问题。在数据流的进化过程中,用户可能对最近到达的数据流更感兴趣,而 Brich,StreamKM++,SWFCM等算法都没有考虑过这个问题。本文在研究了一系列聚类算法基础上,提出了一种基于权值衰减的数据流模糊微簇聚类算法(Weight Decay Streaming Micro Clustering,WDSMC),使用微簇结构提高聚类准确性,使用权值时间衰减结构降低历史数据的影响。
2 基本概念
定义1(数据流模型): 数据流是一个带有时间戳的多维的数据点集合 X1, X2,…,Xs,…。每个数据点 Xi是一个包含d维的数据记录,表示为 Xi=(x1,
定义 2(模糊簇): 给定一个数据X集 = {X1, X2,…,Xn},模糊簇 Cj是X的一个子集,它允许X中每个数据点都具有一个属于jC 的0到1之间的隶属度[15]。
定义 3(隶属度矩阵): 隶属度矩阵U是一个m n× 的矩阵,其中m是需要聚类的簇个数,n是数据点的个数,iju表示第jX 在模糊簇iC 中所占的比重。
关于 iju的取值范围,满足如下两条性质[15]:
性质1 对于每个数据点jX 和簇iC,都有0≤ uij≤ 1。
性质2 对于每个数据点 Xj,都有
定义4(簇中心点): 第i个模糊簇的中心点 iV应该结合隶属度矩阵计算,其计算公式为[9](p的含义见定义5)
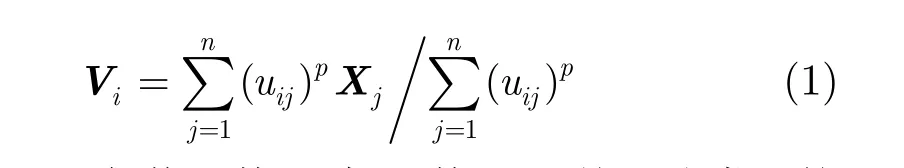
定义5(代价函数/目标函数): 按照聚类C的误差平方和来评价聚类的质量,其公式为[9]
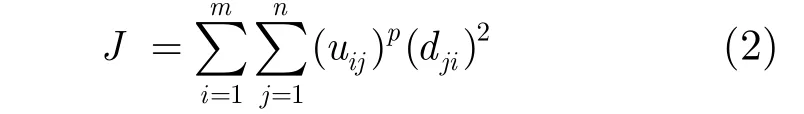
其中,加权指数p( 1p≥ )控制隶属度的影响。p的值越大,隶属度的影响越大; dji=| |Xj-Vi||表示数据点jX 与第i个簇的中心iV的欧式空间距离。
目标函数J的值越小,表明聚类质量越好。要求式(2)取值最小,结合的特点,可以得到隶属度矩阵的计算[9]:
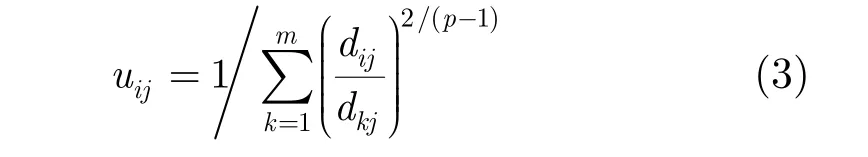
3 基于权值衰减的数据流模糊微簇聚类WDSMC算法
本文提出的基于权值衰减的数据流模糊聚类WDSMC算法是将数据流分块处理,使用改进的带权值模糊 C均值算法(Advanced Weighted Fuzzy Clustering Method,AWFCM)微簇聚类分块后的数据流,在每一部分聚类得到微簇中心点及其权值进入下一部分数据流之前,衰减前一部分数据点权值,减小历史数据对于最近阶段聚类结果的影响。在处理完整个数据流之后,将得到微簇中心及其权值当做数据点,再次调用AWFCM算法处理,最终得到整个数据流上的各个簇中心。
3.1 模糊C均值聚类(FCM)算法及其改进
FCM[9]是一种模糊聚类算法,其算法步骤如表1所示。
从表1可以看出,FCM算法的初始隶属度函数是随机选择的,只要满足性质2即可,即所计算出的初始簇中心也是随机的,与样本数据点无关。因FCM算法是局部收敛的,所以FCM的算法性能强烈依赖于初始簇中心的选择。本文针对上述FCM算法的缺陷,提出了改进FCM算法(AFCM),如表2所示。

表1 FCM算法

表2 改进的FCM算法(AFCM)
从表2中可以看出,AFCM选择距离比较远的数据点作为初始簇中心,这符合簇内对象具有很高相似性,而簇间对象相似性低的要求。降低算法陷入局部收敛的概率,提高聚类质量。为了不陷入局部最优解中,WDSMC算法多次独立调用AFCM算法处理数据流的第1部分,选取使得目标函数值最小的微簇中心及其权值进入数据流的下一部分。而对于数据流的其余部分,上一部分聚类得到微簇中心点就作为下一部分的初始微簇中心点,从而加快收敛速度。
3.2 权值时间衰减与微簇结构
数据流是按照时间顺序依次到达的数据点。随着时间的推进,用户往往更加在意最近到达的数据点所形成的簇。本文提出的WDSMC算法采用权值衰减结构提高最终所形成簇的时效性。
定义 6(数据点权值) 在t时刻,数据点j的权值w定义为
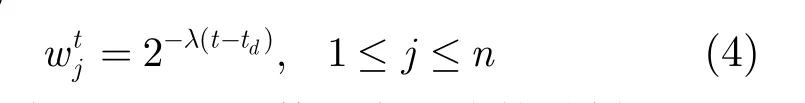
其中λ是衰减因子,dt是数据点到达的时刻。最近到达的数据点的权值为 1,上一部分的数据点权值为2λ-,依次类推。通过给每一个数据附加一个随时间衰减的权值,降低历史数据的影响。由式(4)可见,λ的取值越大,旧的数据衰减的越快,对最终簇的形成影响越小。
定义7(簇权值) 在t时刻,第i个簇的权值cw定义为

即所有数据点在该簇上的隶属度与权值乘积之和表示该簇的权值。每个簇的权值之所以说是随时间衰减,是因为簇中的数据点是随时间衰减的,由式(4)和式(5),可以得出的结论为:
性质3 从t时刻到 1t+ 时刻,第i个簇权值cw将衰减2,即满足式(6):
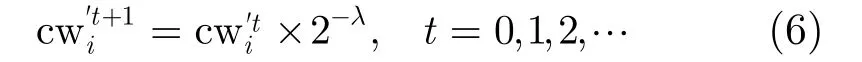
在数据流分块处理过程中,如果仅仅把m个簇的中心点和权值传递到下一部分的数据流中,由于包含的原始数据点信息太少,影响到聚类质量。在WDSMC算法中,每部分按更大的簇个数k进行聚类,称之为微簇。使用微簇可以保留更多的簇中心点和权值,最后使用AWFCM算法将微簇聚类成最终的簇。
3.3 带权值的FCM算法(WFCM)
因为在 WDSMC算法中将每个数据点都赋了一个随时间衰减的权值,所以在使用 FCM算法处理每一部分的数据时必须要考虑到权值的因素。WFCM与FCM的区别在于式(1)和式(3)要加上权值的影响:
式(1)需要变换为式(7):
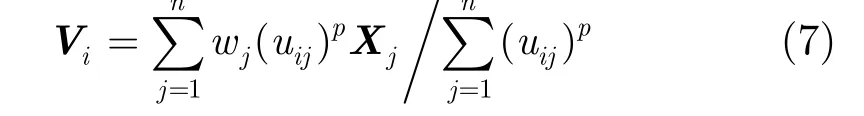
式(2)需要变换为式(8):
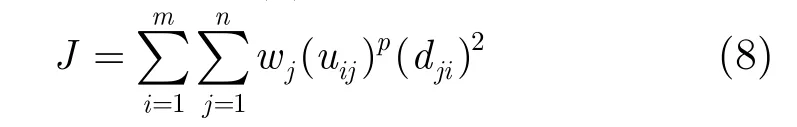
3.4 WDSMC算法框架
本节给出WDSMC数据流聚类算法框架,如图1所示,依据数据流到达时间的次序将数据流分成形如 S1,S2,…,Sp的块,数据块的大小由主机内存的大小决定,记数据块 S1,S2,…,Sp中数据点的个数分别为n1,n2,…,np。
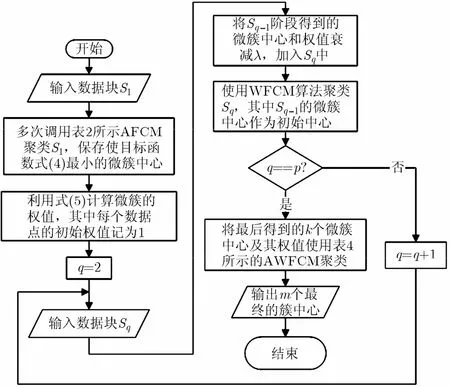
图1 WDSMC算法流程图
每一部分处理过程如下:新到达的数据点的权值记为 1,上一部分计算得到的微簇中心及其权值也当作数据点处理,并使用式(6)对上一部分微簇权值进行衰减处理;依据式(3)计算隶属度,利用式(7)和式(5)计算更新微簇中心及其权值;通过不断地的迭代,使得式(8)达到最小或者到达到某一指定迭代次数。WDSMC算法框架伪代码如表3所示。
在表 3中数据块 Sq(q>1)的处理过程中,是将Sq-1中的微簇中心当作一般的数据点,与Sq中的新的数据点一起聚类。也就是说,算法中所用到的各个方程式中,其数据点个数n是Sq(q>1)中数据点个数与1qS-中微簇个数之和,即满足:n=nq+k。如何通过这k个微簇中心点及其权值得到最终的m个用户需要的簇呢?本文使用表4所示的带权值模糊C均值算法AWFCM来完成该任务。

表3 WDSMC算法框架

表4 AWFCM算法
4 实验结果
本文使用Matlab实现了WDSCM算法,同时实现了用来做比较分析的 SWFCM[10]算法(Matlab实现)和 StreamKM++[7]算法(Microsoft Visual C++实现)。所有的实验都是在一个2G内存、酷睿2双核CPU、操作系统为Windows 7的主机上运行的。SWFCM算法和StreamKM++算是两种常见的数据流聚类算法,其中SWFCM属于模糊聚类算法,而StreamKM++属于硬聚类算法。所有实验的聚类质量评价标准是依据式(2)得到的,即由数据点与簇中心的距离的平方与隶属度乘积之和所决定。
4.1 数据集
本文采用来自真实世界的数据源,以期获得具有实际指导意义的结果。所使用的数据主要来自UCI Machine Learning Repository[16]。表5总结了本文实验即将用到的2个数据集(数据维度不包括类标号):
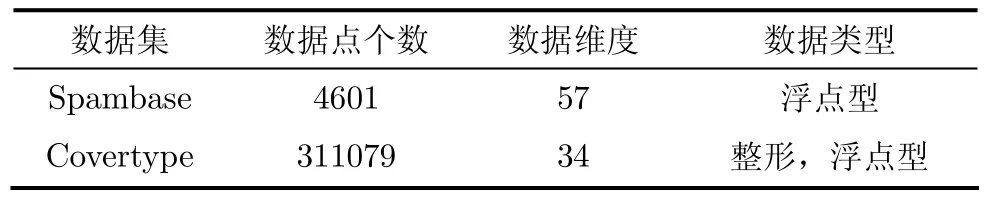
表5 实验使用的数据集
4.2 算法参数
本小节主要介绍 WDSCM以及将要做对比的SWFCM,StreamKM++算法的一些基本的参数设置。StreamKM++所有参数与文献[9]中介绍的一样。SWFCM算法和WDSCM算法在使用FCM或其改进时,最大迭代次数都为50次;计算目标函数的加权指数 3p= ;目标函数达到收敛条件满足其前后值差的绝对值小于10-6。若非特别说明,WDSCM算法的权值时间衰减因子设为 λ= 0.125,微簇个数设为 400k= 。在从微簇得到最终簇的过程中,采用5次独立调用改进的带权值的FCM算法。在处理数据流第 1部分时也是采用 5次独立调用改进的FCM,降低第1部分初始微簇中心随机选择带来的误差。
4.3 λ的取值分析
权值时间衰减因子λ是WDSMC算法中很重要的一个参数,它决定了历史数据对当前簇的影响程度。在本文的其他实验中,λ取一个较小的值0.125,而对于那些需要在最近的数据流上聚类的应用中,可以适当增大λ的值,算法具有很好的灵活性。
本文取λ的值从 0.25到 16,评估算法在Spambase数据流上的聚类效果,其中数据流的每一部分有1000个数据点,最后一部分有601个数据点,最终聚类簇个数 4m= ,微簇个数 80k= ,其余参数设置同上一节所介绍,实验结果图2所示。

图2 λ取值与代价函数的关系-
在图 2中实线段代表最终簇中心在整个Spambase数据集上的目标函数值,虚线段代表最终簇中心在 Spambase最后一部分上的目标函数值。随着λ取值的增加,算法在最近部分的数据上的代价函数越来越小,最近部分的聚类效果越来越好;而在整体数据流上计算的代价函数值不会因为λ在一定范围内增加而有明显的变大,即整体聚类质量不会因为λ的增大而大幅降低。这是本文提出算法的优势所在,提供了一定的灵活性,可以依据具体的应用需求选择合适的λ值。-
4.4 -算法性能对比-
由于是在整个数据集上计算代价函数,为公平起见,在与SWFCM和StreamKM++算法做性能对比时,本文算法暂不考虑权值时间衰减函数的影响,即 0λ= 。每种算法下的聚类代价函数如图 3和图4所示,由于StreamKM++算法是一种硬聚类方法,其模糊聚类下的代价函数是通过将其聚类后的簇中心和原数据集代入式(3)和式(2)所得到的。实验发现,虽然SWFCM算法与StreamKM++算法和WDSMC算法相比在运行时间上是较好的,但是其聚类质量(代价函数越小,聚类质量越高)却不如另外两种算法,特别是随着最终簇个数的增加,与后两种算法之间的差距更加明显。-
与SWFCM和StreamKM++算法相比,本文算法还有如下两点优势:(1)由于本文算法在第1步使用微簇聚类,不需要用户事先指定最终簇的个数。因此可以像Clustream算法一样,将聚类过程分成在线和离线两个部分,只要保留微簇中心及其权值,就可适应聚类成不同最终簇个数的需求。使用微簇即提高了聚类的精确性,又减少了在修改簇个数时需要重新聚类的麻烦。(2)本文算法可以根据需要,适当增大λ值,减小历史数据对聚类的影响,适用于实时性要求高的业务。-
4.5 -微簇聚类最终簇-
在本文前面的实验中,将数据流挖掘得到的微簇二次聚类成最终簇时使用的是表 4所示的AWFCM算法。本节考虑一种不同的微簇聚类成最终簇的方式———遗传模拟退火算法(Simulated- Annealing Genetic Algorithm,SAGA)[17]。该算法将遗传算法和模拟退火算法相结合用于聚类分析,是一种非线性的全局最优化搜索方法,通过不断尝试跳出局部最优解的途径得到优化问题的全局最优解,相对而言FCM算法以及AFCM算法都是一种局部最优搜索方法,故使用该算法对比本文所提出的AFCM算法的聚类效果。-
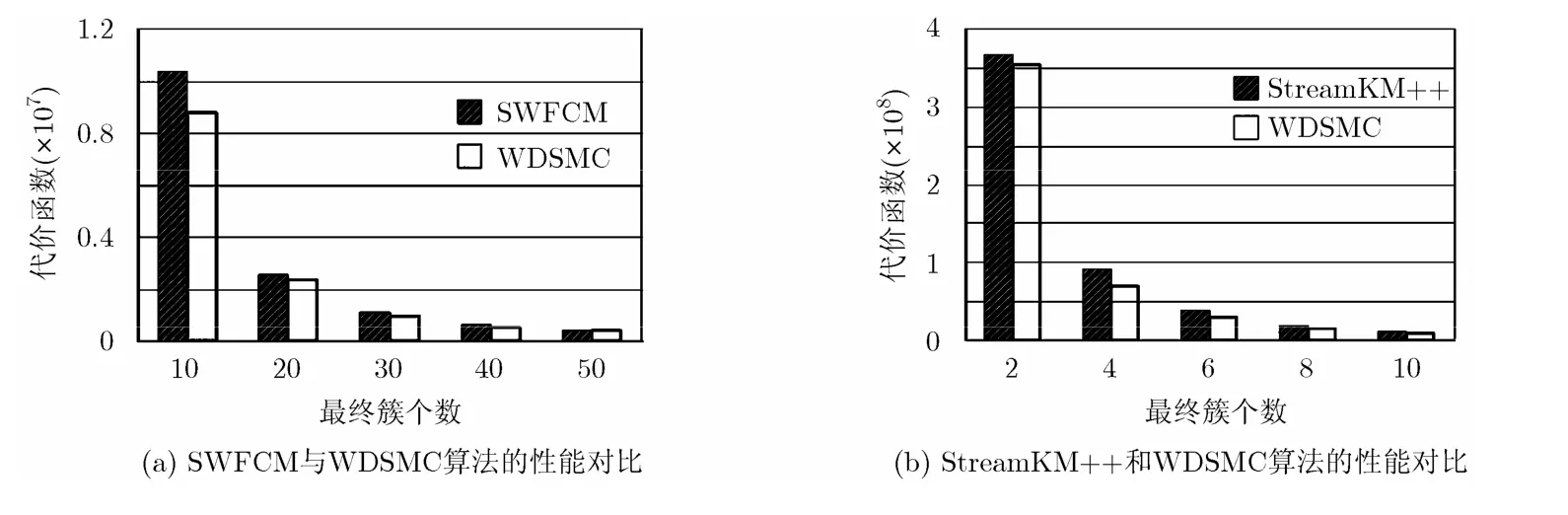
图3 Spambase数据集上实验结果-
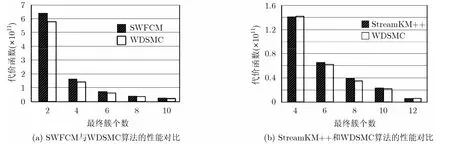
图4 Covertype数据集上的实验结果-
表6列出了AWFCM算法与SAGA算法将Spambase数据集上的微簇聚类成最终簇所用的时间和聚类目标函数对比,其中SAGA算法中的参数设置与文献[17]相同。作为一种非线性优化方-法,模拟遗传退火算法SAGA通过大量的迭代可以达到全局最优的搜索效果,但是需要消耗大量的时间。在表6中,对于实验中Spambese数据集从微簇聚类到最终簇的过程,使~用SAGA算法需要的时间是AWFCM算法的300400倍,而对聚类质量的提升(对应于代价函数的减小)不足 1%。实验证明,改进的带权值的 FCM算法在保证聚类质量的前提下,大大提升了算法的时间效率。
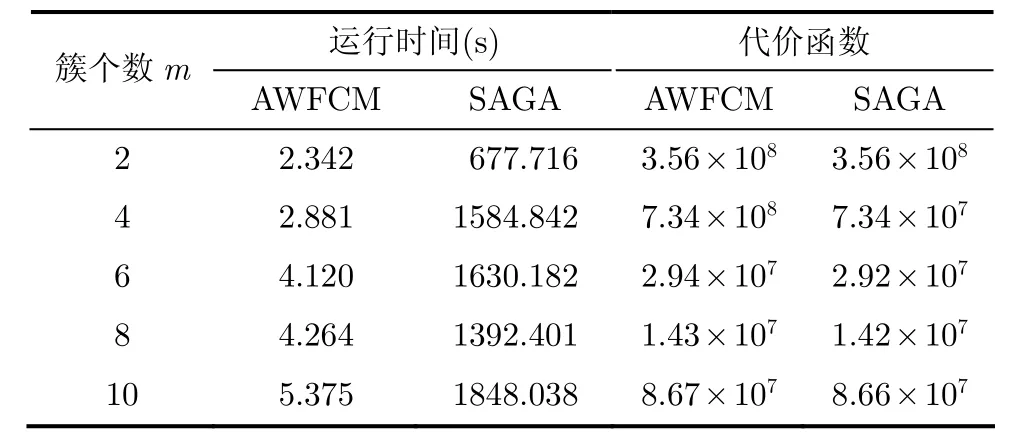
表6 在Spambase数据集上运行时间和代价函数对比
5 结束语
本文提出了一种新的数据流模糊聚类算法。该算法使用微簇结构保存最终聚类所需要的信息,提高聚类质量和自适应最终簇的个数;使用权值时间衰减结构降低历史数据对聚类的影响。通过对不同数据集进行实验表明,本文所提出的WDSCM算法相对于StreamKM++和SWFCM算法而言具有更好的整体聚类效果。在微簇聚类最终簇的过程中分别使用遗传模拟退火算法SAGA和改进的带权值的FCM算法对比算法性能。接下来的工作方向可以包括以下主题:探究每部分数据块大小变化对最终聚类效果的影响;改进微簇结构,以进一步提高聚类质量;关注不同时间段数据流簇的演化情况和在算法加入噪声点的检测处理过程等。
[1] Jonathan A S,Elaine R F,Rodrigo C B,et al.. Data stream clustering:a survey[J]. ACM Computing Surveys,2013,46(1):13:1-13:31.
[2] Shifei D,Fulin W,Jun Q,et al.. Research on data stream clustering algorithms[J]. Artificial Intelligence Review,2013,43(4):593-600.
[3] Tian Z,Raghu R,and Miron L. BIRCH:an efficient data clustering method for very large databases[C]. Proceedings of the ACM SIGMOD International Conference on Management of Data,New York,USA,1996:103-114.
[4] Aggarwal C C,Han J,and Yu P S. A framework for clustering evolving data streams[C]. Proceedings of the 29th Conference on Very Large Data Bases,Berlin,Germany,2003:81-92.
[5] Chen Y and Tu L. Density-based clustering for real-time stream data[C]. Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,New York,USA,2007:133-142.
[6] Cao F,Ester M,Qian W, et al.. Density-based clustering over an evolving data stream with noise[C]. Proceedings of the 16th SIAM International Conference on Data Mining,Maryland,USA,2006:328-339.
[7] Ackermann M R,Märtens M,Raupach C,et al.. StreamKM ++:a clustering algorithm for data streams[J]. Journal of Experimental Algorithmics,2012,17(1):2-4.
[8] Arthur D and Vassilvitskii S. K-means++:the advantages of careful seeding[C]. Proceedings of the 2007 ACM-SIAM Symposium on Discrete Algorithm,New Orleans,USA,2007:1027-1035.
[9] Baraldi A and Blonda P. A survey of fuzzy clustering algorithms for pattern recognition[J]. IEEE Transactions on Systems,Man, and Cybernetics, Part B: Cybernetics,1999,29(6):778-785.
[10] Renxia W,Xiaoya Y,and Xiaoke S. A weighted fuzzy clustering algorithm for data stream[C]. Proceedings of the 2008 ISECS International Colloquium on Computing,Communication,Control,and Management,Guangzhou,China, 2008:360-364.
[11] 郭躬德,李南,陈黎飞. 一种基于混合模型的数据流概念漂移检测算法[J]. 计算机研究与发展,2014,51(4):731-742.
Guo Gong-de,Li Nan,and Chen Li-fei. Concept drift detection for data stream based on mixture model[J]. Journal of Computer Research and Development,2014,51(4):731-742.
[12] 胡伟. 一种改进的动态 k-均值聚类算法[J]. 计算机系统应用,2013,22(5):116-121.
Hu Wei. Research and realization of a web information extraction and knowledge presentation system[J]. Application of Computer System,2013,22(5):116-121.
[13] 李子柳. 大数据实时流式聚类框架研究[D]. [硕士论文],中山大学,2013. Li Zi-liu. A framework for real time stream clustering of big data[D]. [Master dissertation],Sun Yat-sen University,2013.
[14] Hossein M K,Suhaimi I,and Javad H. Outlier detection in stream data by clustering method[J]. International Journal of Advanced Computer Science and Information Technology,2013,2(3):25-34.
[15] Jiawei H,Micheline K,Jian P. 范明,孟小峰. 数据挖掘:概念与技术[M]. 第3版,北京:机械工业出版社,2012:323-350.
[16] David Aha. UCI Machine Learning Repository[OL]. https:// archive.ics.uci.edu/ml,2014.
[17] 史峰,王辉,郁磊,等. Matlab智能算法:30个案例分析[M].北京:北京航天航空大学出版社,2011:188-196.
孙力娟: 女,1963年生,博士,教授,博士生导师,研究方向为演化计算、无线传感器网络和数据处理等.
陈小东: 男,1992年生,硕士生,研究方向为数据挖掘、数据处理.
韩 崇: 男,1985年生,博士,讲师,研究方向为多媒体信息处理、数据挖掘.
郭 剑: 男,1978年生,博士,副教授,硕士生导师,研究方向为无线传感器网络、无线多媒体传感器网络.
New Fuzzy-Clustering Algorithm for Data Stream
Sun Li-juan①②Chen Xiao-dong①Han Chong①Guo Jian①②
①(College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
②(Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
There is a great challenge in the data stream clustering due to a limitation of time and space. In order to solve this problem,a new fuzzy-clustering algorithm,called Weight Decay Streaming Micro Clustering (WDSMC),is presented in this paper. The algorithm uses a reformed weighted Fuzzy C-Means (FCM) algorithm,and improves the quality of clustering by the structures of micro-clusters and weight-decay. Experimental results show that this algorithm has better accuracy than Stream Weight Fuzzy C-Means (SWFCM) and StreamKM++ algorithm.
Data mining;Data stream;Fuzzy C-Means (FCM);Weight decay;Micro-clustering
TP301
A
1009-5896(2015)07-1620-06
10.11999/JEIT141415
2014-11-05收到,2015-03-20改回,2015-06-01网络优先出版
国家自然科学基金(61171053,61300239),教育部博士点基金(20113223110002),中国博士后科学基金(2014M551635)和江苏省博士后科研资助计划项目(1302085B)资助课题
*通信作者:孙力娟 sunlj@njupt.edu.cn
