浅谈三角函数解题技巧

湖南省邵阳市隆回县万和实验学校 范才伍

一、三角知识的基础性

1.对三角函数性质的考查

三角函数的性质主要包括;单调性、奇偶性、周期性、对称性、有界性等性质，解答此类题型的一般技巧是先进行三角恒等变换，将函数化成y＝Asin(ωx＋ψ)+K的形式后，再把ωx＋ψ看成整体利用正弦函数的性质解题。关键是把ωx＋ψ看成整体。

例：设函数f(x) =sin(ωx+ φ) + c os(ωx+ φ)(ω ＞ 0),的最小正周期为π，且f(-x) =f(x)，则

A.f(x)在单调递减

B.f(x)在单调递减

C.f(x)在单调递增

D.f(x)在单调递增

精讲精析：

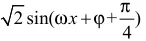
2.对三角恒等变换的考查

变换是重要的数学方法与工具，三角恒等变换可以改变三角函数式的结构、形式，化简三角函数式，以下是三角恒等变形基本策略，在进行三角变换时，必须考虑变换的目的、方向以及变换的依据与方法等。

一是三角恒等变形的突破口：常为对角的特征分析、对函数名称进行分析、对幂指数进行分析等。

二是三角恒等变形的基本策略。

（1）化弦（切）法 。

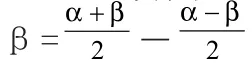
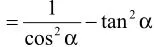
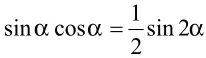
（5）引入辅助角。

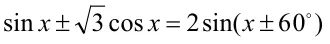
例：已知，求sin2θ-sinθ.cosθ+2cos2θ的值.

精讲精析：

解：原式=

.

说明：利用齐次式的结构特点（如不具备，通过构造的办法得到如上题的分母“1”的代换），进行弦、切互化，就会使解题过程简化。

3.对三角函数的图像和图像变换的考查

（1）三角函数y＝Asin(ωx＋ψ)+K 的图像的作法有五点作图法和变换法作图

五点作图法的一般步骤：列表、描点、连线。

关键是把ωx＋ψ看成一个整体，取0、、π、、2π五个值列表。

变换法作图的一般步骤：

将y＝sinx的图像

由函数y=Α s in(ωx+ φ)+Β 的图像求其解析式求法

技巧：由图像观察当x=x1时，取得最小值为ymin；当x=x2时，取得最大值为ymax，(x1与x2在一个周期内）则Α=(ymax-ymin)，Β=(y+y)，maxmin=x2-x1(x1＜x2)，ω=,；再把函数的零点或最值点坐标代入解析式，解三角方程可得φ的值。

二、三角知识的工具性

1.三角函数与解三角形的综合问题

三角形中的三角函数问题，已经逐渐成为高考命题的一个热点。它们的解决大都以三角函数的基本知识为基础，以应用正弦定理、余弦定理、面积公式以及三角公式为手段，考查转化化归能力，判断求解能力，以及应用知识分析解决实际问题的能力。

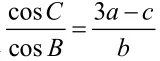
(1)求sinB的值；(2)若b=4 2，且a=c，求 ∆ABC面积。

精讲精析：

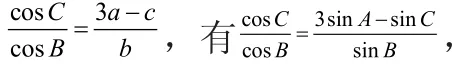
即sinBc osC=3sinAc osB- sinCc osB，所以sin(B+C)=3sinAc osB，

又因为A+B+C=π，sin(B+C)=sinA，所以sinA=3sinAc osB，因为sinA≠0，所以，又0＜B＜π，所以。

法二留给读者思考。

(2)在∆ABC中，由余弦定理可得，又a=c，

所以有=32，即a2=24，所以∆ABC的面积为S=。

方法提炼：在解决含有边、角关系的三角形中的三角函数问题时，基本的解题思路有两条，一是利用正弦定理与余弦定理把边的关系都转化为角的关系，通过三角恒等变换解决问题；二是利用正弦定理与余弦定理把角的关系都转化为边的关系，通过代数变换解决问题，但多数情况下是把边的关系都转化为角的关系，利用熟悉的三角变换公式解题。常用公式是正余弦公式。

2.三角函数与平面向量的综合问题

例 ： 已 知a→＝(cosα,sin α),b→=(cosβ,sin β)，0＜ β ＜ α ＜π.(1)若,求证：;(2)设,若,求α,β的值.

思路点拨：题（1）应用求模公式可得，题（2）应用向量坐标相等公式解方程组即可。

精讲精析：

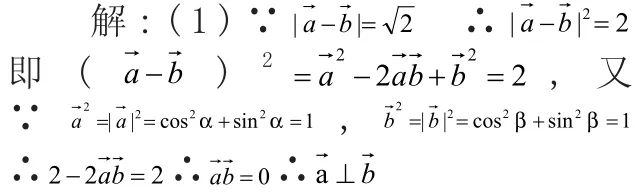
技巧点拨：本题体现了三角函数问题与向量问题的等价转化思想，而是实现向量与实数互化的依据和桥梁。

练习：已知向量

(1)若，求tanθ的值；（Ⅱ）若|a|=|b|，0＞θ＞π求θ的值。