UV-Inscribed Optical Fiber Gratings in Mid-IR Range and Their Laser Applications

Zhongyuan Sun, Zhijun Yan, Kaiming Zhou, Qizhen Sun,Abdulyezir Ayomipo Badmos, and Lin Zhang

1. Introduction

Since in-fiber gratings were demonstrated by Hill et al.in 1978[1], a variety of application devices based on optical fiber gratings have been developed. So far, fiber Bragg gratings as the most common in-fiber devices have been used in many applications, such as telecommunications and sensors[2],[3], fiber laser systems, pump laser stabilizers[4],gain flattening filters[5], WDM systems[6], and chromatic dispersion compensators[7]. In the earlier development period, optical fiber gratings were mostly classified into two categories: (i) fiber Bragg gratings (FBGs), based on forward to backward core mode coupling and offering wavelength selective reflection function and (ii)long-period gratings (LPGs), based on forward core to cladding mode coupling and offering loss filter function.

In the last ten years, optical fiber gratings with tilted structure have gained more attention from researchers due to their distinctive optical properties. The ability to couple light from the core mode to cladding and radiation modes by the tilted fiber gratings (TFGs) was first reported in 1990 by Meltz et al.[8]. Subsequently, Erdogan and Sipe[9]gave a theoretical analysis of TFG structures and also pointed out the in-fiber polarizer function of 45°-TFG structure, as it can couple the p-polarized light out of fiber core and leave the s-polarized light propagating through the fiber. Basically, fiber grating devices are a periodic form of modulation of the refractive index (RI) of the fiber core.This RI modulation structure can be introduced by exposing a silica glass fiber to an ultraviolet laser (UV) with a typical wavelength in the range of 244 nm to 248 nm[10].

In recent years, the optical fiber devices operating at mid infrared (mid-IR) spectrum have attracted growing interests due to their application potentials in defense[11],health[12],[13], and the environment[14]. Optical fiber gratings as useful in-fiber components are in demand to extend their operation wavelength range from near-IR into mid-IR.Moreover, laser sources locating at eye-safe 2 μm region,especially for operation wavelengths in the atmospheric transmission window between 2.05 μm and 2.3 μm, have been attracted special attention. However, most of the reported mid-IR fiber lasers used the bulk mirrors in the cavities, inducing high insertion loss and limiting the structure compactness. FBGs can be used as intra-cavity resonators for all fiber lasers to eliminate these disadvantages. Therefore, the fabrication of FBGs covering all mid-IR wavelength range is the key factor for the development of all fiber mid-infrared lasers. Besides, the 45°-TFG can be employed as an in-fiber polarizer in amid-IR mode-locked fiber laser providing the effect of nonlinear polarization evolution (NPE)[15]and as well as low insertion loss and high compactness.

This paper is constructed as follows. In Section 2, we discuss briefly the mode coupling mechanism and phase matching conditions for three types of gratings-Bragg,long-period and tilted structures. In Section 3, the three main in-fiber grating fabrication techniques are described,including two-beam holographic, phase-mask, and pointby-point, all of them have been employed to fabricate the mid-IR fiber gratings reported in this paper. In Section 4,we report the characteristics of mid-IR FBGs, LPGs, and 45°-TFGs in terms of thermal, strain, and RI response, as well as polarization dependent loss (PDL), respectively. In Section 5, we present the results on a multi-wavelength continue wave (CW) mid-IR fiber laser utilizing a set of FBGs with Bragg wavelengths in mid-IR range and a mode locked mid-IR fiber laser using a 45°-TFG with PDL function in mid-IR wavelength range to tailor the nonlinear polarization evolution. The overall conclusions are given in Section 6.

2. Principles of Optical Fiber Gratings

Normally, the bound wave can be coupled to the counter-propagating or co-propagating modes in a structure perturbed optical fiber. According to the mode coupling direction, optical fiber gratings can be divided into two types. One is a backward-coupled grating in that the incident light is coupled from forward-propagating core mode to the backward-propagating one, forming FBGs and small angle TFGs. The other type is forward-coupled gratings in which the light is coupled from forwardpropagating core mode to co-propagating cladding modes,forming LPGs and large angle TFGs.

For the transfer of energy from a mode into another propagating mode, the phase mismatch factor βΔ is referred to a detuning, which is written as

whereiβ is the propagation constant for the incident mode,dβ signifies the diffracted mode propagation constant, Λgis the grating period, θ is the tilt angle of grating and letter N expresses an integer number (0, 1, 2,…). Otherwise the sign ‘±’ represents the situation thereof the mode propagates in z∓direction.

When the phase-matching condition satisfies βΔ =0,(1) can be rewritten as:

Bothiβ anddβ share the same sign for counterpropagating modes. In contrast, they have opposite signs for co-propagating mode. The first-order diffraction is dominant with regards to most cases, hence N=1[16]. The resonant wavelength should be

In the case of normal FBG (θ=0), the Bragg wavelength is shown by

where neffis the effective index of the core and Λ is the FBG period.

Fig. 1 below shows a diagram of an FBG structure and the coupling from the forward to the backward core mode.

Fig. 1. Schematic of mode coupling of an FBG.

The phase matching condition for an LPG (coupling from the core mode into the co-propagating cladding mode)is given by

where ncois the effective index of the core mode andcl,mn is the effective index of the mth cladding mode. Λ is the period of grating, which usually is in an order of several hundred microns. Fig. 2 shows a diagram of an LPG structure and mode coupling in co-propagating modes.

Fig. 2. Schematic of mode coupling of an LPG.

In the case of TFGs, the mode couplings are possible in both directions (i.e. the core mode can be coupled to the counter-propagating mode or co-propagating mode),depending on the magnitude of the grating tilt angle. The phase match wavelength for a TFG is given as below[17],[18]:

where ncoandcl,mn are the effective indexes of the core and mth cladding mode, respectively. The “+” indicates the coupling to the counter-propagating mode whereas “-” to the co-propagating mode. The grating period along the fiber axis can be simply expressed as:where Λgis the normal period of the grating. The schematics of TFGs with mode coupling in forward and backward directions are shown in Fig. 3.

Fig. 3. Schematic of TPG mode coupling: (a) backward coupling and (b) forward coupling.

3. Mid-IR Fiber Grating Fabrication

3.1 Fabrication Methods of Optical Fiber Grating

A. Two-Beam Holographic Technique

The two-beam holographic method was demonstrated by Meltz and his colleagues in 1989[19]. This technique for writing a grating structure from the side of the fiber involves a system of an amplitude splitting interferometer,by which the fiber gratings can be carved for a wide wavelength range (presently 750 nm to 2300 nm). The diagram of an experimental setup for the grating writing using two-beam holographic method is shown in Fig. 4.

Fig. 4. Schematic diagram of optical set-up using the two-beam holographic technique.

In the system shown in Fig. 4, the UV laser beam is divided into two beams with equivalent power by the 50:50 beam splitter. Then, these two beams are reflected by two different mirrors and intersected together on the fiber core to generate interfering UV intensity fringes. Due to the UV light absorption, the refractive index of the core is modified along fiber length. The main advantage of the two-beam holographic method is to write FBGs with arbitrary Bragg wavelength by simply changing the angle (2α) between the two beams. However, this technique is associated with some disadvantages, such as low sustainability to mechanical vibrations, limited to short length grating and relatively poor quality of the grating. Hence some wave front-splitting interferometers have been proposed to solve some problems, including the Prism interferometer and the Lloyd interferometer[20]which give better coherence and stability.

B. Phase Mask Technique

The phase mask technique was first demonstrated by Hill[21]and Anderson et al.[22]in 1993. Although this method is just for fiber gratings with fixed wavelengths, it is widely used as one of the most effective techniques for reproducible and high quality FBG inscription. A phase mask is a corrugated surface-relief grating etched in a fused silica plate. With UV beam at normal incidence, the radiation is diffracted into several orders, m= 0 , ±1,± 2 ,…. A phase mask can be optimized to suppress the light diffraction energy in 0 order and maximize diffraction efficiency in the ±1 diffracted orders, which are the two beams to generate fringes in the fiber core. As shown in inset of Fig. 5, an interference pattern is produced by the superposition of ±1 orders of diffracted beams from a phase mask, which can be used to write FBG structure.

Fig. 5. Schematic of experimental arrangement for fabricating normal and complex structure gratings using the UV beam scanning across a phase mask.

Fig. 5 also shows the experimental arrangement of phase-mask technique for fiber grating fabrication in the photonics laboratory at Aston University. The UV laser is focused by a cylindrical lens, which is transversely-mounted on a PC-controlled translation stage. The UV beam passes through the phase mask and to the fiber placed behind the phase mask. With the movement of translation stage along the fiber length, the grating structure can be written in the core of fiber by the scanning UV beam.

The main advantage of the phase-mask technique is capable of producing high quality and complex grating structures such as chirped, apodized, Moiré, sampled and phase-shifted gratings. However, the drawback of this technique is that the gratings of different wavelengths require different phase masks.

C. Point-by-Point Technique

The third common grating fabrication method is the point-by-point technique, which is usually used to fabricate LPGs with period ranging from 10 μm to 600 μm. Due to limit on the focused size of UV beam, it is difficult to write 1st order Bragg gratings which have normal periods of～0.5 μm at 1550 nm and it has been used to write 2nd and 3rd order Bragg gratings[23].

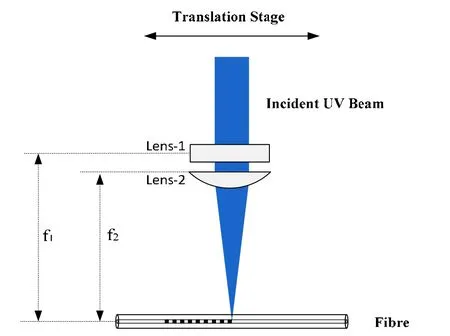
Fig. 6. Schematic diagram of the point-by-point technique.

As shown in Fig. 6, compared to the phase-mask inscription system, one more cylindrical lens is added to the point-by-point system to focus the UV beam down to the size of the fiber core. In the point-by-point fabrication system, a PC controlled shutter is used to modulate the laser power by switching on/off with a 50:50 duty cycle to achieve point by point writing. The mid-IR LPGs described below is fabricated by using this point-by-point method.

3.2 Optical Fiber Grating Inscriptions in Mid-IR Range Review Stage

A. Inscription of FBGs

The mid-IR FBGs reported in this paper were fabricated by a 244 nm UV source from a frequency doubled Ar+laser (Coherent Sabre Fred®) using the twobeam holographic technique. The two-beam holographic technique for writing grating structure from the side of fiber is a flexible technique allowing inscribing FBGs with arbitrary wavelengths ranging from 750 nm to 2300 nm in our laboratory. We fabricated mid-IR FBGs with centered wavelengths from 1800 nm to 2225 nm. A super continuum broadband light source (Fianium SC480, UK) was employed to monitor the FBG growth during the UV inscription. The mid-IR FBGs were UV-inscribe in Corning SM-28 and Thorlabs SM-2000 fibers to compare their characteristics.Note that, before the FBG inscription, both SM-28 and SM-2000 fibers were hydrogen loaded under high-temperature (80°C) and high-pressure (150 bar) for 2 days to increase their UV-photosensitivity. However, a great quantity of hydroxide ions in the hydrogen loaded fiber caused strong light absorption in the wavelength range from 1800 nm to 1900 nm[24]. Fig. 7 shows the transmission spectra of SM-28 fiber with and without hydrogen loaded.

Fig. 7. Transmission spectra of SM28 fiber with and without hydrogen loading and measured using the supercontinuum light source from 1700 nm to 2200 nm.

Fig. 8. Measured transmission spectra of FBGs inscribed on SM28 and SM2000 fibers.

It is clear that there is a broad absorption peak between 1830 nm and 1900 nm on the hydrogen loaded fiber.Therefore, the FBGs with Bragg resonances in this absorbing wavelength range were not possibly monitored in the fabrication process, but were measured after the annealing treatment, which out-gas the hydrogen from the fiber. All mid-IR FBGs were annealed at 80°C for 48 hours to out-gas residual hydrogen and to improve their long term stability. Fig. 8 shows the measured transmission spectra of three FBGs inscribed in the SM-28 and three in SM-2000 fibers centered at ～1800 nm, ～2050 nm, and ～2225 nm,respectively. From Fig. 8, we can see that the transmission loss peaks of the six FBGs reach around 16 dB to 20 dB,corresponding to a reflectivity of 96-99%; the 3 dB bandwidths (FWHMs) are all less than 0.4 nm. It also can be seen that the FBGs UV-inscribed in SM-28 fiber are stronger with slightly high reflectivity and broad bandwidth than that in SM-2000 fibers.

B. Inscription of LPGs

The LPGs of periods from 200 μm to 450 μm were written in hydrogen loaded Corning SM-28 fiber by using the same 244 nm UV laser and point-by-point technique.The UV beam scanning speed was selected in the range of 0.1 mm/s to 0.3 mm/s and the duty cycles were 50%. Using the super continuum broadband light source and an optical spectrum analyzer with spectral range extended to 2.4 μm(Yokogawa AQ 6375), the transmission spectra of fabricated mid-IR LPGs were measured. Fig. 9 shows the transmission spectrum of an LPG with a length of 20 mm and a period of 200 μm. From the figure, we can clearly see that there are three broad attenuation resonant peaks distributed from near-IR (1200 nm) to mid-IR (2400 nm)range, and two of them are at 2 μm region. The transmission loss peak at 2000 nm is relatively weak and the one at 2183 nm exhibits a loss of 8.2 dB. The bandwidth of resonances in mid-IR region is typically ＞10 nm, much broader than that of an FBG. LPGs are transmission loss type devices,which have been employed for a range of applications in optical fiber communications and sensing, and these LPGs could translate the applications to mid-IR range.

Fig. 9. Transmission spectrum of an LPG with 200 μm period UV-inscribed in SMF-28 fiber by the point-by-point method.

C. Inscription of 45°-TFGs

The 45°-TFGs centered at ～2000 nm were also UV inscribed into SMF-28 fiber by using the phase-mask scanning technique and the same UV laser. The phase-mask(Ibsen, Denmark) has a 25 mm long uniform pitch and 33.7°tilted angle with respect to the fiber axis. The designed phase mask tilted angle at 33.7° is to ensure the internal titled index fringes are at 45° in the fiber core. Before the inscription, the SMF-28 fiber was hydrogen loaded to enhance photosensitivity. After the inscription, the grating samples were subjected to annealing treatment at 80°C for 48 hours to stabilize the grating structure. A high magnification microscope system (Zeis Axioskop 2 mot plus)under a 100×oil immersion objective lens was employed to examine the grating structure. Fig. 10 shows a micro-image of the 45°-TFG in the fiber core of SM-28 fiber. It can be seen clearly from the figure that the tilted angle of grating pattern is measured at 44.98° and the diameter of fiber core is 8.77 μm. The effective length of the TFG was 24 mm.

Fig. 10. Microscopic image of the 45°-TFG taken under a 100×oil objective lens.

4. Sensitivity and Polarization Characteristics of Mid-IR Fiber Gratings

4.1 FBG Characters

The effective refractive index (RI) and the period space between each FBG plane will be affected by temperature and strain changes. The FBG central wavelength depends on the effective RI of the core and the periodicity of the grating. So we can deduce that the FBG center wavelength shifts due to temperature and strain changes. From (4), the sensing theoretical equation is given by

whereBλΔ is the wavelength shift, TΔ and lΔ are the variations in temperature and fiber grating length,respectively.

The first term in above equation represents the thermal effect of a FBG which corresponds to the grating space change and the thermo-optical induced change in the effective RI. Therefore, the first term also can be written as

whereλBis the Bragg wavelength, i.e., the central wavelength of FBG, α = ( 1 Λ )(∂ Λ ∂T )is the fiber thermal

Λexpansion coefficient, and αΛ=(1 neff) (∂ neff∂T) is the thermo-optical coefficient.

In the following experiment, three FBGs with different wavelengths fabricated in SM-28 fiber by the two-beam holographic technique, which were introduced in Section 3.2, were employed to investigate the thermal response characterization of FBG.

Fig. 11. Experimental setup for FBG thermal characterization.

The experimental set up is illustrated in Fig. 11. The grating region, which is around 10 mm long, of the fiber was placed in the heating device controlled by a temperature controller (Light wave LDT-5910B). The temperature was varied from 0°C to 80°C at a step of 10°C.For each temperature, the FBGs resonance was measured and recorded by the OSA (Optical Spectrum Analyzer).From Fig. 12, it can be seen that the three FBGs with different wavelength exhibit different thermal responses.The temperature sensitivities are ～15.4 pm/°C, ～15.9 pm/°C,and ～16.3 pm/°C for the FBGs with the central wavelengths at 1950 nm, 2000 nm, and 2100 nm, respectively, which states that the longer the FBG central wavelength is, the higher the temperature sensitivity is.

Fig. 12. Comparison of thermal responses for three FBGs with different wavelengths.

The second term in (8) represents the strain effect of a FBG. The strain expansion leads to the change of the effective refraction index and the grating period of the FBG,resulting in the wavelength shift which can be written as

where peis an effective strain-optic constant, defined as

The experimental set up for FBG strain characterization is shown in Fig. 13. The FBG was straightly clamped on two 3D moving stages set at a distance of 40 cm. The varied strain was supplied to the grating by moving the right stage from 0 mm to 0.35 mm at a step of 0.05 mm. Fig.14 presents the strain responses of the three FBGs measured by the OSA. It can be seen that the strain sensitivities are ～1.47 pm/με, ～1.51 pm/με, and ～1.56 pm/°C for the FBGs with the central wavelength at 1950 nm,2000 nm, and 2100 nm, respectively, which demonstrates that the FBG with the Bragg resonance in longer wavelength range also exhibits higher strain sensitivity than that in shorter wavelength range, and specially the strain.

Fig. 13. Experimental setup for FBG strain characterization.

Fig. 14. Comparison of the strain responses for three FBGs with different wavelengths.

4.2 LPG Characters

The light coupling from the fundamental core mode to the cladding modes of LPG generates multiple resonant peaks, which are intrinsically sensitive to the changes in environment, such as the temperature and the surrounding medium refractive index (RI).

The effect of the temperature variation on the coupled cladding modes of LPG depends on the contribution of the material and waveguide properties of the fiber. Therefore,the thermal induced resonant wavelength of LPG shifts according to the following equation:where λ is the central wavelength of the LPG resonant peak,T is temperature, ηeffis the effective index of the core mode,ηcladis the effective index of the cladding mode, L is the length of the LPG and Λ is the grating period. Similar to the FBGs used for temperature sensing experiment, the LPGs were also UV-inscribed in hydrogenated standard telecom SM-28e fiber with a grating length of 15 mm and thermally annealed after UV-inscription to stabilize their structure and properties. The same experimental set-up shown in Fig. 11 was used for LPG thermal response characterization.

Fig. 15. Comparison of the thermal response for two different resonant peaks of the LPG.

We have examined the thermal responses for two different resonant peaks of the LPG with the grating period of 200 μm. The temperature was elevated from 20°C to 80°C with an increment of 10°C, and the experimental results of the wavelength shift are plotted in Fig. 15. It is clear that the longer resonant wavelength corresponding to higher order cladding mode has higher temperature sensitivity. Extraordinarily, the temperature sensitivity of the resonant peak at 2100 nm reaches to 112.5 pm/°C,which is over 50% larger than that of only 73.2 pm/°C at the 1200 nm resonant peak.

Furthermore, the changes of the surrounding medium RI will also affect the wavelength shift of the resonant peaks, and the RI sensitivity of LPG can be expressed as[25]

where nsuris the RI of the surrounding medium,cleff,mn is the effective refractive index of the mth cladding mode and λmis the central wavelength of the LPG resonance. From(13) we can see that for different cladding mode,is very distinct and higher order cladding mode is expected to be more sensitive to the RI change in the environment,which provides ideal sensors for biochemical and biomedical sensing.

To evaluate the surrounding medium RI sensing capability of the LPGs, we applied a series of refractive index oil (from Cargille laboratory) with different RIs from 1.3 to 1.44 to the LPG, and measured its spectral evolution using the experimental setup shown in Fig. 16. To avoid the wavelength shift induced by bending and axial strain, the grating was straightly clamped on two stages set at the same height. The refractive index oil was placed on a flat glass substrate, which can be raised by a vertical micrometer to submerge the grating into the refractive index oil without imposing any force to the grating. Once the grating was surrounded by the refractive index oil, the shift of wavelength was almost instantaneously observed on the OSA. After each index oil measurement, the grating was rinsed with methanol to remove the residual oil till the original spectrum in air was restored.

Fig.16. Schematic of the experimental setup for refractive index sensing of LPG.

Fig. 17. Refractive index sensing results for 200 μm LPG with 2 different resonant peaks.

Fig. 17 plots the wavelength shifts of 2 different resonant peaks for the LPG with the grating period of 200 μm when it is subjected to 15 refractive index gels.Unlike the temperature response, the shorter wavelength resonant peak of the LPG corresponding to lower order cladding mode is more sensitive to RI change of the surrounding medium than the longer wavelength resonant peak. Quantitatively, the RI sensitivity of the shorter wavelength resonant peak of the LPG (at 1200 μm) is about 198.72 nm/RIU which is almost twice that at longer wavelength (2100 μm) which is 107.52 nm/RIU.

4.3 45°- TFG Characters

It is well known that when unpolarized light is incident on a boundary between two media with different refractive indices by Brewster angle, the light reflected from the boundary is therefore totally polarized and the refracted light will be partially polarized. By using the Snell’s law[26]and Fresnel equations[27], the Brewster angle can be calculated as

where n1is the refractive index of the initial medium and n2is the refractive index of the other medium. In a fiber grating, n1and n2are equal to the effective refractive indices of core without and with UV modification,respectively. However, since the UV induced refractive index modulation is as small as at the order of (10-5～ 10-3),n2≈n1. Thus, in a UV-inscribed fiber grating, the Brewster’s angle is θB= arctan(n2n1) = arctan(1) = 45°. Hence, the 45°-TFG can be recognized as an ideal in-fiber polarizer,which couples the s-polarized light out of fiber core and leave the p-polarized light propagating through the fiber(see Fig. 18).

As discussed above, the 45°-TFG can be recognized as an ideal in-fiber polarizer. Thus, polarization dependence loss (PDL) or the polarization extinction ratio (PER) is the important parameter of a 45°-TFG. The PER is a measure of the peak-to-peak difference in transmission of an optical component or the ratio of the maximum and the minimum transmission of a system with respect to all possible states of polarization[28]. The PER of the 45°-TFG was measured by using the polarization scanning technique. The typical experimental setup is shown in Fig. 19 (a). In this setup, the light source is a super continuum source which can generate light from 450 nm to 2400 nm. The polarizer(Thorlabs LPNIRA050-MP) is a bulk component which has a high PER of ＞50 dB at a range from 1550 nm to 2450 nm.To measure the PER of the 45°-TFG at a specific wavelength, the central wavelength of optical spectrum analyzer (Yokogawa AQ6375) was set at the measuring wavelength, and the span was set to zero. The maximum and minimum transmissions through the 45°-TFG can directly be measured by adjusting polarization controller.Fig. 19 (b) depicts the simulated and measured PER of the 45°-TFG within the range from 1600 nm to 2400 nm. The simulation method we used is the volume current method,of which the details have been reported in [29], [30]. In the simulation, we set the fiber core radius to 4.5 μm, the period of grating to 0.990 μm, and the length of grating to 24 mm. The refractive index modulation induced by the UV light was set to 0.0017. It is observed that the simulation result agrees well with the experimental result. The measured bandwidth of PER is broader than 400 nm and the PER is larger than 12 dB from 1850 nm to 2150 nm.Although the PER of the 45°-TFG at 2000 nm (～24 dB) is still low compared to the commercial in-line polarizers at 1550 nm (～40 dB), it is comparable with current commercial in-line polarizers at 2000 nm (～25 dB).Moreover, the PER of the 45°-TFG could be further increased by extending the length of grating and optimizing the UV scanning power and speed. Using the same setup,we also measured the insertion loss of the 45°-TFG, which was essentially identical at ～0.6 dB within the range of 1850 nm to 2150 nm.

Fig. 19. Experimental setup and measured PER: (a) experimental setup of PER measurement of 45°-TFG and (b) measured PER at the range from 1800 nm to 2200 nm.

5. Applications on Mid-IR Fiber Lasers

5.1 FBGs Applied in Multi-Wavelength Tm-Doped CW Fiber Laser

The schematic diagrams of two Tm3+-doped silica laser systems exploiting the in-fiber reflection function of mid-IR FBGs are shown in Fig. 20: (a) using one FBG as high reflectivity (HR) mirror and the 0°-cleaved fiber end as an output coupler and (b) using one HR FBG as mirror and one low reflectivity (LR) FBG as an output coupler.The active fiber used in these two systems is a 11-meter double cladding Tm3+-doped fiber (Nufern,SM-TDF-10P/130-HE) with an octagonal shaped pump core with a diameter of 130 µm across the circular cross-section and a numerical aperture (NA) of 0.46. The fiber has a 10 µm core diameter with a reduced NA of 0.15 by a specific pedestal around the core. The Tm3+dopant concentration in the fiber core is about 5 wt.% and the measured absorption coefficient at 793 nm is ～3.0 dB/m.Two 793 nm diode lasers (Lumics, German) with 105/125µm core and cladding parameter multimode fiber pigtail were used as the pump source and the light was coupled into the double cladding Tm3+-doped fiber through a(2+1)×1 pump combiner (ITF, USA). The maximum launched pump power was 8W. At the output end, either the fiber end facet (～3.5% Fresnel reflection) (Fig. 19 (a)) or LR FBG (Fig. 19 (b)) was employed to provide laser feedback and also act as the output coupler. A number of UV-inscribed FBGs with the Bragg reflection wavelengths between 1900 nm and 2200 nm at a span of ～25 nm were used in the laser system for multi-wavelength output operation. The HR FBG was designed with reflectivity of ＞95% and a spectral FWHM of ＜0.4 nm, and the LR FBG was designed with reflectivity of ～50% and a spectral FWHM of ＜0.4 nm. Because the threshold for Fresnelreflection-based cavity might be lower than that for the FBG-based cavity at some wavelengths of small gain, the fiber end at the FBG side was angle-cleaved at 8° to reduce the reflection in order to avoid the parasitic lasing. At the output side, a Germanium window was employed to remove the residual pump light.

By using the setup shown in Fig. 20 (a), the narrow width CW laser with selectable wavelength between 1975 nm and 2150 nm was achieved. Fig. 21 shows the spectra of lasers centered at 1974.7 nm, 1997.5 nm, 2026.2 nm, 2056.8 nm, 2074.3 nm, 2102.4 nm, 2125.7 nm, and 2151.02 nm at the maximum pumping power of 8.0 W measured in a large spectrum range of 400 nm.

Fig. 20. Experimental setup of Tm3+-doped silica fiber laser with counter-propagating scheme employing: (a) ～3.5% reflectivity fiber end as output coupling reflector and (b) ～ 50 % reflectivity FBG as output coupling reflector.

Fig. 21. Output spectra of Tm3+-doped fiber lasers at 400 nm spectrum range for the cavity constructed by perpendicularly cleaved fiber end and HR FBGs. From left to right, the laser operation center wavelengths are at1974.7 nm, 1997.5 nm, 2026.2 nm, 2056.8 nm, 2074.3 nm, 2102.4 nm, 2125.7 nm, and 2151.02 nm, respectively. The scanning resolution was at 0.5 nm.

Fig. 22. Output spectra of Tm3+-doped fiber laser for the cavity constructed by perpendicularly cleaved fiber end and HR FBGs with different center wavelengths. The scanning range and resolution were 1 nm and 0.02 nm, respectively.

The spectra of the lasers were also measured in a 1.0 nm range with a resolution of 0.02 nm to investigate their spectrum characteristics, as shown in Fig. 22. It is observed that the FWHMs of laser lines were all narrower than 0.3 nm, suggesting the efficient spectral confining ability of the HR FBGs. Note that the spectrum gradually tended to be compressed and smoothed with increasing output wavelength owing to the weakened ground state re-absorption process at longer wavelength region. At the shorter wavelength emission region, especially below～2000 nm, the spectrum was broader and exhibited more amplitude fluctuation as a result of strong ground state re-absorption and re-emission processes. After the center wavelength exceeding ～2100 nm, the spectrum width was essentially unchanged, suggesting that the laser was almost not influenced by the re-absorption owing to the fairly low absorption cross-section of less than 0.1×10-25m2.

In order to investigate the laser wavelength operation limit of our Tm3+-doped silica fiber, higher feedback was added by employing LR FBG to replace the previously cleaved fiber end as the output coupler, as shown in Fig. 20(b). The short and long operation wavelength edges were then extended to 1925.6 nm and 2198.4 nm respectively.Fig. 23 shows the measured spectra across 400nm spectrum range at the maximum pumping power of 8.0 W.0.02 nm, respectively.

Fig. 23. Output spectra of Tm3+-doped fiber laser at 400 nm spectrum range for the cavity constructed by LR FBG and HR FBG. From left to right these center wavelengths are at 1925.6 nm,1951.2 nm, 2174.9 nm, and 2198.4, respectively. The scanning resolution was set at 0.5 nm.

Fig. 24. Output spectra of Tm3+-doped fiber laser for the cavity constructed by LR FBGs and HR FBGs with different center wavelengths. The scanning range and resolution were 1 nm and

The spectra of the lasers under each LR FBG at a narrow scanning range of 1.0 nm were also measured at the maximum pumping power of 8 W to examine the detailed spectrum characteristics as shown in Fig. 24 with center wavelengths of 1925.6 nm, 1951.2 nm, 2174.9 nm, and 2198.4 nm, respectively. The operation wavelength of 2198.4 nm is also the longest wavelength produced from 3F4→3H6transition of Tm3+ions so far being demonstrated.Similar to the results as shown in Fig. 22, the laser at 1925.6 nm and 1951.2 nm still exhibited the spectrum fluctuation and broadening, whereas the laser at 2174.9 nm and 2198.4 nm showed fixed spectrum width of 0.8 nm and relatively smooth and narrow spectrum.

It is well known that there are many methods of tuning or switching the wavelength of a fiber laser, such as strain tuning an FBG, fiber etalons, external diffraction grating,fiber coupled acousto-optic tunable filters, and so on. By employing an FBG array in the laser cavity and inducing bend loss between adjacent FBGs in the array, the experiment setup of a six wavelengths switchable Tm3+-doped fiber laser was demonstrated, as shown in Fig. 25.

Fig. 25. Experiment setup of multi-wavelength switchable Tm3+-doped silica fiber laser.

Fig. 26. Transmission and output spectrums: (a) transmission spectrum of the FBG array and (b) output spectra of the multi-wavelength switchable Tm3+-doped fiber laser.

An FBG array including 6 FBGs centered at 1997 nm,2025 nm, 2057 nm, 2075 nm, 2103 nm, and 2125 nm,respectively, were fabricated and its transmission spectrum is shown in Fig. 26 (a). It is observed that the emission cross-section decreases with the wavelength, however, the gain and threshold are not coincidence with the emission cross-section. We arranged these FBGs in descending order,as 1997 nm (FBG1), 2125 nm (FBG2), 2025 nm (FBG3),2103 nm (FBG4), 2075 nm (FBG5), and 2057 nm (FBG6).Then one end of the array was spliced to the Tm3+-doped fiber with the opposite end cleaved at 8° while the other end of the cavity was cleaved perpendicularly to provide 3.6% Fresnel reflection (FR) for all wavelengths. The pigtails between adjacent FBGs in the array were looped around two tubular mounts at a radius of 5 cm. With this setup, the wavelength can be switched freely by increasing the distance between the two tubular mounts after the selected FBG to induce the bend loss for the suppression on all other laser modes relevant to rest FBGs. Through mode competition, the laser mode relevant to the selected FBG can win owing to its lower threshold. Fig. 26 (b) shows the measured spectra from output side.

Fig. 27. Schematic of the mode-locked double-clad Tm3+-doped fiber laser based on NPR.

5.2 45°-TFG Applied in Mode Locked Fiber Laser

The experimental arrangement for the nonlinear polarization rotation (NPR) mode-locked double-clad Tm3+-doped fiber based on mid-IR 45°-TFG is shown in Fig. 27. Two 793 nm diode lasers with maximum pumping power up to 7.56 W were launched through a (2+1)×1 pump combiner to 7.0 m double-clad Tm3+-doped fiber with an octagonal shaped inner cladding with 128 µm diameter and 0.45 numerical aperture (NA), and fiber core with 10µm diameter and 0.22 NA. The measured absorption at 793 nm is ～4.0 dB/m. The selected fiber length of 7.0 m provides ＞95% pump absorption efficiency. A polarization independent optical isolator with an insertion loss of 0.76 dB and an extinction ratio of 35 dB at 2 µm was used to ensure the unidirectional laser operation. A 45°-TFG and a pair of polarization controllers (PC1 and PC2) positioned before and after the 45°-TFG form the NPR based saturable absorber. A 95:5 fiber coupler centered at 2 µm with an insertion loss of 0.62 dB was employed to output 5% laser power from the cavity. The measured splicing loss was～0.3 dB due to the mismatch of the NA between the active fiber and SMF-28 fiber. Note that the coupling ratio chosen as 95:5 is to increase the cavity power for ensuring enough nonlinear phase shift difference. The SM-2000 fiber designed for 2 μm operation with a cut-off wavelength at 1.7 μm was chosen as the passive fiber in the NPR for the merit of its relatively low background loss and bend loss around 2 µm compared to SMF-28 fiber. The length of SM-2000 fiber was optimized to 95.0 m to ensure enough nonlinear phase shift difference for stable mode-locking as well.

The total length of this mode-locked fiber laser cavity is 105.0 m including 7.0 m Tm3+-doped fiber, 95.0 m SM-2000 fiber and 3.0 m SMF-28 pigtail fiber from the pump combiner, isolator and coupler. The anomalous dispersion values of the Tm3+-doped fiber and the SM-2000 fiber at 1.993 µm were about -84 ps2/km and -73 ps2/km respectively, which are provided by the fiber producer. The dispersion of the SMF-28 at 1.993 µm was estimated to be-80 ps2/km according to the measured dispersion value at 1.9 µm [31]. Thus, the net dispersion in the cavity was estimated to be ～ -7.76 ps2, suggesting that the laser was operating at a large anomalous dispersion regime. For the measurements of the laser output, an InGaAs photo detector(EOT ET-5000F) with a response time of approximately 28 ps connected to a 2.5 GHz digital oscilloscope was used to measure the pulse train and pulse waveforms. The pulse duration was measured by an interference auto-correlator(APE, Germany).

Since the net group velocity dispersion (GVD) is anomalous, the counter-balance between the GVD and self-phase modulation (SPM) is to generate soliton pulses.Initially, the oscillator started to operate at continuous wave regime at a launched pump power of 1.229 W. Then,self-staring multiple soliton pulses were observed by adjusting the two PCs at a launched pump power of 1.320 W.It is well known that the NPR in this laser cavity is power dependent. Only at sufficient pumping and nonlinear polarization rotation, the mode-locking can be self-started.In our experiment, the pump was increased to a value capable of generating enough nonlinear polarization rotation for initiating the mode-locking, but the power in the cavity has beyond the limitation of single soliton pulse.Therefore, the multiple soliton pulses were generated firstly and then the single soliton pulse was achieved by decreasing the pump power, as similar to the soliton regime in [32] and [33]. Gradually reducing the pump power from 1.320 W to 1.232 W, the reduction of wave-breaking in soliton from multiple pulses to 4-, 3-, and 2-pulses, and finally a stable single pulse at a slope efficiency of 6.2%, as shown in Fig. 28 (a). The measured pulse waveform and sequence at this launched pump power are also shown in the inset of Fig. 28 (a). The obtained repetition rate of 1.902 MHz matches well with the theoretically cavity length dependent value, suggesting that only one pulse was generated per round trip. Maximum output power of 142 μW was achieved for the single pulse regime corresponding to a pulse energy of 74.6 pJ. Note that this energy includes the energy in the Kelly sidebands, and it is much larger than the theoretically calculated limited output energy of 13 pJ for the single soliton based on the formula in [34]. Once the mode locking was achieved by the initial adjustment of the PCs, the single pulse operation can be achieved by reducing the pump power from self-starting multiple pulses and no longer needed to adjust the PCs. Fig. 28 (b) shows the measured interference and intensity autocorrelation trace of the mode-locked pulses at a scanning range of 10 ps. The shoulder to peak ratio is 1:8, confirming that the oscillator operated at typical solitary mode-locking regime. The FWHM is 3.4 ps corresponding to the pulse duration of 2.2 ps when sech2-pulse fit is assumed. Fig. 28 (c) shows the optical spectrum of the soliton pulses with a resolution of 0.05 nm. The central wavelength and FWHM were 1992.7 nm and 2.02 nm, respectively, thus giving a time-bandwidth product of 0.335, indicating the pulse is almost transform-limited. Typical Kelly sidebands originating from spectral interference of dispersive waves were observed,suggesting that the operation in this case was the conventional solitary mode-locking. Moreover, the absence of additional narrow spectral line also confirms that continuous wave components have been blocked. Fig. 28 (d)shows the RF spectrum of the output at fundamental frequency for a scanning range of 10 kHz with a resolution of 100 Hz. The signal noise ratio of ～60.5 dB and the absence of modulation in 20 MHz broad RF spectrum [see inset of Fig. 28 (d)] indicate that it is stable mode-locking and no Q-switching modulation. The smooth noise floor also indicates that the oscillator operates with low amplitude noise.

Fig. 28. Solitary operation of a Tm3+-doped mode-locked fiber laser utilizing a mid-IR 45°-TFG as an intracavity polarizer: (a)output power as a function of launched pump power, inset: pulse waveform and sequence at single soliton regime; (b) interference and intensity autocorrelation with sech2-pulse fitting; (c) optical spectrum; and (d) RF spectrums with scanning range of 10 kHz and 20 MHz (inset).

The laser can also be switched to stable noise-like regime by adjusting the PCs as the pump ramps up to 1.82 W, as shown in inset of Fig. 29 (a). The measured repetition rate of 1.902 MHz indicates that the oscillator operated at the fundamental mode-locking regime. Fig. 29 (b) shows the measured interference and intensity autocorrelation trace at a scanning range of 150 ps. A narrow spike riding on a broad pedestal extended over the entire measurement window was observed, which was the typical autocorrelation trace of noise-like mode-locking[31],[35]. A typical smooth and broad optical spectrum for noise-like pulses shown in Fig. 29 (c) reveals a center wavelength of 1994.2 nm and FWHM of 18.1nm. Fig. 29 (d) is the RF spectrum at a scanning range 10 kHz with a resolution of 100 Hz. The lower signal noise ratio of ～47 dB compared to that of solitary pulses is still in the typical range of 40 dB～50 dB for NPR-based noise pulses[32],[36], but much lower than that obtained in nonlinear optical loop mirror(NOLM)structure[37]. No side lobes were observed in the RF spectra which are always obvious in the noise-like regime,suggesting the absence of appreciable fluctuations of pulse duration. The noise-like mode-locking state can be maintained to the maximum launched pump power of 7.56 W at a slope efficiency of 7.5%, yielding maximum output power of 475.8 mW. This corresponds to 250.1 nJ per noise-like pulse bundle. Such high pulse energy and high spike peak power could lead to some potential applications involving laser radar, large electric field interactions with molecules, material processing, and pump source of mid-IR super-continuum generation.

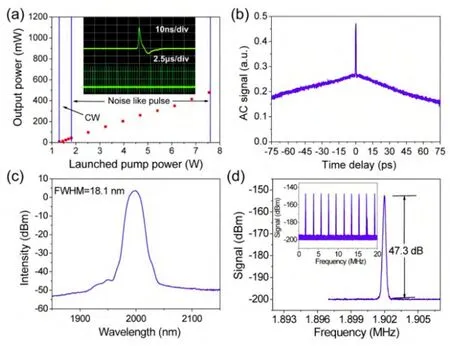
Fig. 29. Noise-like regime operation: (a) output power as a function of launched pump power at the CW and noise-like regime, inset: pulse waveform and sequence on oscilloscope; (b)interference and intensity autocorrelation with sech2-pulse fitting;(c) optical spectrum; and (d) RF spectrums with scanning range of 10kHz and 20MHz (inset).

6. Conclusions

We have successfully UV-inscribed FBGs, LPGs, and 45°-TFGs in mid-IR wavelength range on the standard telecom single mode SM-28 and mid-IR single mode SM-2000 fibers. The mode coupling mechanisms of these three types of optical fiber gratings have been discussed and the phase matching conditions for FBG, LPG and TFG have been presented. We also discussed the three common in-fiber grating fabrication techniques; including two-beam holographic, phase mask and point-by-point systems, which have been used to fabricate the mid-IR optical fiber gratings described in this paper. The temperature and strain sensitivity characteristics for the mid-IR FBGs, the temperature and refractive index response for mid-IR LPGs,and the polarization property for mid-IR 45°-TFGs have been investigated. Finally, we presented the application of mid-IR fiber gratings in selectable multi-wavelength CW and mode locking Tm3+-doped fiber lasers. In the former,the laser operation at eight individual wavelengths in the range from 1925.6 nm to 2198.4 nm by using LR and HR FBGs was successfully demonstrated and in the later, we have experimentally demonstrated the soliton and noise-like pulses delivered from an all-anomalous all-fiber Tm3+-doped fiber ring cavity oscillator based on the mid-IR 45°-TFG.

[1] K. O. Hill, Y. Fujii, D. C. Johnson, and B. S. Kawasaki,“Photosensitivity in optical fiber waveguides—Application to reflection filter fabrication,” Appl. Phys. Letters, vol. 32 no. 10, pp. 647-649, 1978.

[2] R. Kashyap, “Optical fibre Bragg gratings for applications in telecommunications,” in Proc. of the 21st European Conf.on Optical Communication, 1995, pp. 23-26.

[3] A. D. Kersey, M. A. Davis, H. J. Patrick, M. LeBlanc, K. P.Koo, C. G. Askins, M. A. Putnam, and E. J. Friebele, “Fiber grating sensors,” J. Lightwave Technol., vol. 15, no. 8, pp.1442-1463, 1997.

[4] B. F. Ventrudo, G. A. Rogers, G. S. Lick, D. Hargreaves, and T. N. Demayo, “Wavelength and intensity stabilization of 980 Nm diode-lasers coupled to fiber Bragg gratings,”Electronics Letters, vol. 30, no. 25, pp. 2147-2149, 1994.

[5] M. Rochette, M. Guy, S. LaRochelle, J. Lauzon, and F.Trepanier, “Gain equalization of EDFA's with Bragg gratings,” IEEE Photonic Tech. Letters, vol. 11, no. 5, pp.536-538, 1999.

[6] M. Ibsen, M. K. Durkin, M. J. Cole, and R. I. Laming,“Optimised square passband fibre Bragg grating filter with in-band flat group delay response,” Electronics Letters, vol.34, no. 8, pp. 800-802, 1998.

[7] F. Ouellette, “Dispersion cancellation using linearly chirped Bragg grating filters in optical waveguides,” Opt. Letters,vol. 12, no. 10, pp. 847-849, 1987.

[8] G. Meltz, W. W. Morey, and W. H. Glenn, “In-fiber Bragg grating tap,” presented at Optical Fiber Communication Conference, San Francisco, 23 January 1990.

[9] T. Erdogan and J. E. Sipe, “Tilted fiber phase gratings,” J.Opt. Soc. Am. A, vol. 13, no. 2, pp. 296-313, 1996.

[10] P. J. Lemaire, R. M. Atkins, V. Mizrahi, and W. A. Reed,“High-pressure H2loading as a technique for achieving ultrahigh UV photosensitivity and thermal sensitivity in GeO2doped optical fibers,” Electronics Letters, vol. 29, no.4, pp. 1191-1193, 1993.

[11] S. W. Henderson, C. P. Hale, J. R. Magee, M. J. Kavaya, and A. V. Huffaker, “Eye-safe coherent laser radar system at 2.1 μm using Tm,Ho:YAG lasers,” Opt. Letters, vol. 16, no. 10,pp. 773-775, 1991.

[12] D. E. Johnson, “Use of the Holmium-Yag (Ho Yag) laser for treatment of superficial bladder-carcinoma,” Laser Surg.Med., vol. 14, no. 3, pp. 213-218, 1994.

[13] F. T. Sun, W. T. Zhang, Y. Zhuang, Q. Y. Dong, and A. W. Li,“Application of endoscopic Ho: YAG laser incision technique treating urethral strictures and urethral atresias in pediatric patients,” Pediatric Surgery International, vol. 22,no. 6, pp. 514-518, 2006.

[14] N. Sugimoto, N. Sims, K. Chan, and D. K. Killinger,“Eye-safe 2.1-μm Ho lidar for measuring atmospheric density profiles,” Opt. Letters, vol. 15, no. 6, pp. 302-304,1990.

[15] C. Mou, H. Wang, B. G. Bale, K. Zhou, L. Zhang, and I.Bennion, “All-fiber passively mode-locked femtosecond laser using a 45º-tilted fiber grating polarization element,”Optics Express, vol. 18, no. 18, pp. 18906-18911, 2010.

[16] A. Yariv, “Coupled-mode theory for guided-wave optics,”IEEE Journal of Quantum Electronics, vol. 9, no. 9, pp.919-933, 1973.

[17] T. Erdogan, “Cladding-mode resonances in short- and long-period fiber grating filters,” J. Opt. Soc. Am. A, vol. 14,no. 8, pp. 1760-1773, 1997.

[18] K. S. Lee and T. Erdogan, “Fiber mode coupling in transmissive and reflective tilted fiber gratings," Appl.Optics, vol. 39, no. 9, pp. 1394-1404, 2000.

[19] G. Meltz, W. W. Morey, and W. H. Glenn, “Formation of Bragg gratings in optical fibers by a transverse holographic method,” Opt. Letters, 14, pp. 823-825, 1989.

[20] P. Langenbe, “Higher-order lloyd interferometer,” Appl.Optics, vol. 9, no. 8, pp. 1838-1841, 1970.

[21] K. O. Hill, B. Malo, F. Bilodeau, D. C. Johnson, and J.Albert, “Bragg gratings fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask,” Appl. Phys. Letters, vol. 62, no. 10, pp. 1035-1037,1993.

[22] D. Z. Anderson, V. Mizrahi, T. Erdogan, and A. E. White,“Production of in-fiber gratings using a diffractive optical-element,” Electronics Letters, vol. 29, no. 6, pp.566-568, 1993.

[23] B. Malo, K. O. Hill, F. Bilodeau, D. C. Johnson, and J.Albert, “Point-by-point fabrication of micro-bragg gratings in photosensitive fiber using single excimer pulse refractive-index modification techniques,” Electronics Letters, vol. 29, no. 18, pp. 1668-1669, 1993.

[24] O. Humbach, H. Fabian, U. Grzesik, U. Haken, and W.Heitmann, “Analysis of OH absorption bands in synthetic silica,” J. Non-Cryst. Solids, vol. 203, no. 1, pp. 19-26,1996.

[25] H. J. Patrick, A. D. Kersey, and F. Bucholtz, “Analysis of the response of long period fiber gratings to external index of refraction,” J. Lightwave Technol., vol. 16, no. 9, pp.1606-1612, 1998.

[26] C. B. Mou, H. Wang, B. G. Bale, K. M. Zhou, L. Zhang, and I. Bennion, “All-fiber passively mode-locked femtosecond laser using a 45 degrees-tilted fiber grating polarization element,” Optics Express, vol. 18, no. 18, pp. 18906-18911,2010.

[27] M. J. Adamst, An Introduction to Optical-Waveguides, 1st ed. New York: Wiley, 1984, ch. 2, pp. 11-15.

[28] L. E. Nelson, C. Antonelli, A. Mecozzi, M. Birk, P. Magill,A. Schex, and L. Rapp, “Statistics of polarization dependent loss in an installed long-haul WDM system,” Optics Express,vol. 19, no. 7, pp. 6790-6796, 2011.

[29] Y. F. Li, M. Froggatt, and T. Erdogan, “Volume current method for analysis of tilted fiber gratings,” J. Lightwave Technol., vol. 19, no. 10, pp. 1580-1591, 2001.

[30] Z. J. Yan, C. B. Mou, K. M. Zhou, X. F. Chen, and L. Zhang,“UV-inscription, polarization-dependant loss characteristics and applications of 45 degrees tilted fiber gratings,” J.Lightwave Technol., vol. 29, no. 18, pp. 2715-2724, 2011.

[31] Q. Wang, T. Chen, B. Zhang, A. P. Heberle, and K. P. Chen,“All-fiber passively mode-locked thulium-doped fiber ring oscillator operated at solitary and noise like modes,” Opt.Letters, vol. 36, no. 19, pp. 3750-3752, 2011.

[32] L. Zhang, A. R. El-Damak, Y. Feng, and X. J. Gu,“Experimental and numerical studies of mode-locked fiber laser with large normal and anomalous dispersion,” Optics Express, vol. 21, no. 10, pp. 12014-12021, 2013.

[33] M. Engelbrecht, F. Haxsen, A. Ruehl, D. Wandt, and D.Kracht, “Ultrafast thulium-doped fiber-oscillator with pulse energy of 4.3 nJ,” Opt. Letters, vol. 33, no. 7, pp. 690-692,2008.

[34] W. Qing, G. Jihong, J. Zhuo, L. Tao, and J. Shibin,“Mode-Locked Tm/Ho-Codoped fiber laser at 2.06μm,”IEEE Photonics Technol. Letters, vol. 23, no. 11, pp.682-684, 2011.

[35] Q. Q. Wang, T. Chen, M. S. Li, B. T. Zhang, Y. F. Lu, and K.P. Chen, “All-fiber ultrafast thulium-doped fiber ring laser with dissipative soliton and noise-like output in normal dispersion by single-wall carbon nanotubes,” Appl. Phys.Letters, vol. 103, no. 1, pp. 11103(1)-11103(3), 2013.

[36] L. M. Zhao, and D. Y. Tang, “Generation of 15-nJ bunched noise-like pulses with 93-nm bandwidth in an erbium-doped fiber ring laser,” Appl. Phys. B, vol. 83, no. 4, pp. 553-557,2006.

[37] J. Li, Z. Zhang, Z. Sun, H. Luo, Y. Liu, Z. Yan, C. Mou, L.Zhang, and S. K. Turitsyn, “All-fiber passively mode-locked Tm-doped NOLM-based oscillator operating at 2-μm in both soliton and noisy-pulse regimes,” Optics Express, vol. 22,no. 7, pp. 7875-7882, 2014.