压杆稳定方程的一般表达式
2015-07-12周博文武仁杰
谢 昊 周博文 武仁杰
(郑州大学 土木工程学院,郑州 450001)
压杆稳定方程的一般表达式
谢 昊 周博文 武仁杰
(郑州大学 土木工程学院,郑州 450001)
压杆稳定方程是借助静力法,结合平衡二重性的静力特征,利用位移参数不全为零,系数行列式 D=0所得出的,它受水平约束与竖直约束的影响而略有不同。本文经过论证发现:在竖向约束 时,压杆稳定方程的6种形式存在一般表达式。
压杆稳定方程 平衡二重性 一般表达式
0 引言
结构的强度、刚度和稳定性是保证结构安全可靠的三要素。前两项曾经是设计师们考虑的重点,但随着多起重大工程结构稳定性破坏的发生,稳定性问题愈来愈受到重视。《结构力学》作为将杆件作为主要研究对象的重要力学学科,自然会提及压杆稳定性计算的重要性。然而一般压杆稳定方程的表达受水平约束与竖直约束的影响而略有不同。不方便进行记忆与归一的理解。故而本文重要探求在竖向约束时,一般压杆稳定方程的6种形式的一般表达式。
1.压杆稳定方程的一般表达式
(1)由材料力学得平衡微分方程:

(2)求解平衡微分方程
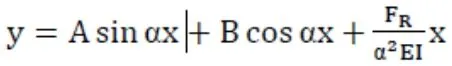
(3)边界条件

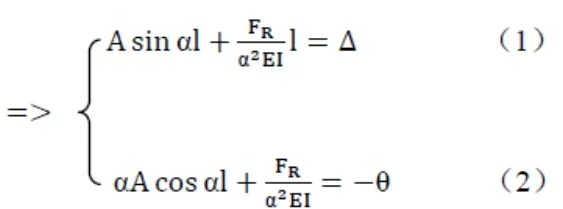
又由
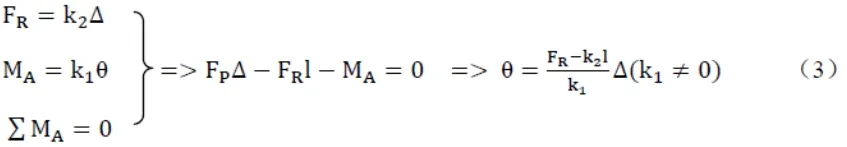
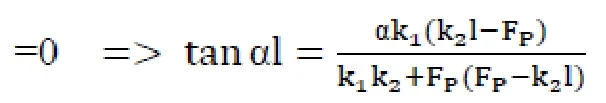
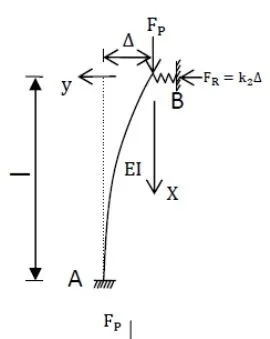
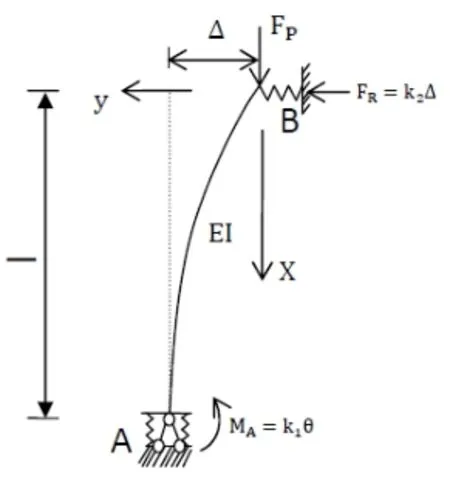
2.具体约束条件下压杆稳定方程的表达式
(1)当k1=∞,A处为固定端,如图2.1所示:
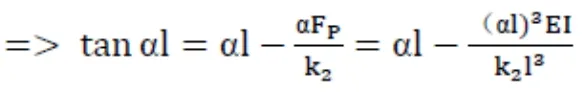
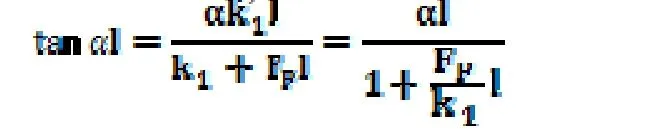
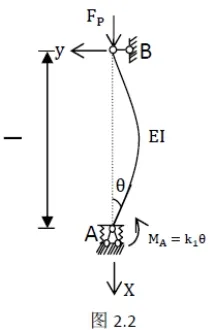
此时
(3)当k2=0,B处无任何水平约束,如图2.3所示:

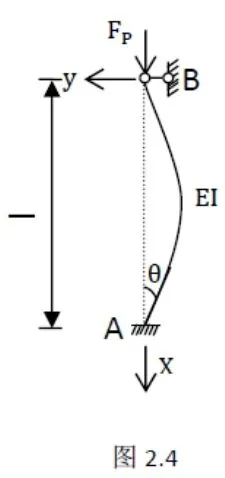
(4)当k1=∞,k2=∞A处为固定端,B处为水平铰支座,如图2.4所示:此时
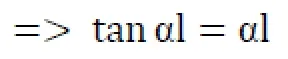
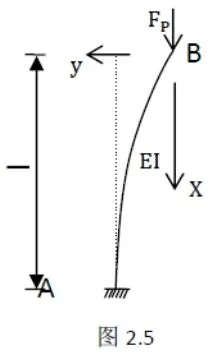
(5)当,A处为固定端,B处无任何水平约束,如图2.5所示:
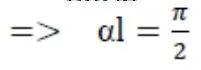
2.结论
本文借用静力法等知识推得压杆稳定方程的一般表达式,并结合教材与教辅书验证具体约束条件下压杆稳定方程的表达式与按压杆稳定方程的一般表达式所推得完全一致。得出结论:在竖向约束时,一般压杆稳定方程的6种形式存在一般表达式,即
[1] 樊友景,高洪波.结构力学[M].郑州:郑州大学出版社,2012.
[2] 黄淑森.结构力学专题教程同步辅导及习题全解[M].北京:中国水利水电出版社,2009.
Buckling equation in general form
Xie Hao Zhou Bowen Wu Renjie
(School of civil engineering of Zhengzhou University, Zhengzhou 450001,China)
Buckling equations is gotten by using the static method, combined with a balanced static characteristic of duality, using displacement parameters are all zero, factor determinants derived from D=0. It will be slightly different under the influence of horizontal restraints and vertical constraints. After detailed discussion,the paper found that when the vertical constraint , six forms of buckling equation exist general expression.
Buckling equations balance of duality general expression
G322
B
1007-6344(2015)09-0054-01
