林木植物的全基因组选择
2015-07-12凌青根
田 郎 译,凌青根 校
(1.中国热带农业科学院橡胶研究所,海南 儋州 571737;2.中国热带农业科学院科技信息研究所,海南 海口 571101)
林木植物的全基因组选择
田 郎1译,凌青根2校
(1.中国热带农业科学院橡胶研究所,海南 儋州 571737;2.中国热带农业科学院科技信息研究所,海南 海口 571101)
基因组选择(GS,也称全基因组选择)是利用捕捉到一个乃至多个数量性状大多数基因位点的全基因组标记估计基因组育种值(即所有标记效应的总和),并以此对目标性状进行选择的方法。目前,这种新的选择方法正在给家畜育种实践带来一场革命性的变化。同样的方法和设想也适用于林木育种。事实上,漫长的世代时间以及大多数复杂性状晚期表达的特性历来都是林木育种所面临的巨大困难和挑战。不仅如此,林木植物还具备诸多其它的有利条件有助于GS的开展和应用,例如:易于收集并建立较大的参考群体且某些性状已作过准确的表型分析;一些改良群体的连锁不平衡(LD)程度较高,这其中包括林木高世代育种程序中所常用到的一些有效群体大小(Ne)较小的群体。本研究利用确定性方程就LD(通过Ne和标记间距离进行模拟),训练集的大小,性状遗传力,以及数量性状位点(QTL)的数目等因素对GS的预期准确性的影响进行了分析评估。结果显示,GS有可能使树木育种的有效性得到根本性的提高。当Ne≤30时,即便标记密度仅大约2个标记/厘摩(cM), 采用GS就能达到传统BLUP(最佳线性无偏预测)选择的基准精度。不过,当Ne较大时,标记密度则需达到20个标记/cM。采用GS可使育种周期缩短50%,进而使育种效率增加100%或以上。随着技术的快速进步和基因分型成本的下降,我们谨慎而乐观地看好GS在加速树木育种进程和提高育种效率上的巨大潜力。不过,在将此项技术推广应用之前,尚需作进一步的模拟研究及概念验证试验。
基因组选择;有效群体大小;连锁不平衡;标记辅助选择(MAS)
通过标记辅助选择(MAS)加速林木育种的进程已成为当今对一些重要林木物种实施基因组计划的主要依据和推动力。完成一个育种周期需经历漫长的世代时间,建立和维持大规模后裔试验费用高昂,以及大多数目标性状遗传力低下一直以来都是林木常规育种所面临的巨大困难,不过,采用MAS策略将有助于克服这些难题[1,2,3]。尽管MAS在林木育种上具有潜在的优势,但基于众多理由,该项技术早先并未被大多数林木育种计划所采纳,而今天看来这些理由大多数确有其合理性[4]。在当时除了成本及技术障碍之外,主要的问题是人们在较大的林木随机交配群体中发现的连锁不平衡(LD )非常有限,所观察到的标记-数量性状位点(QTL)关联往往都局限于特殊的遗传背景。
尽管人们对MAS持有某些怀疑的看法,但对于该项技术的应用前景却一直秉持着乐观的态度,而且随着人工栽培树种大量性状QTL位点的成功鉴定,该领域的研究得以迅速发展。借助RFLP、RAPD、AFLP以及微卫星等分子标记连锁图的构建,人们可以对林木数量性状的遗传组成作出进一步的解析。不过,早期的研究大都局限于主效QTL位点[5,6,7],而且正如通过“Beavis”效应所预测到的那样,由于样本较小,很多位点的效应很可能被高估[8]。此后,当人们采用样本较大的后代群体,而且表型分析也愈加精确之后,对于数量性状的遗传解析(包括QTL位点的数量、分布及效应等)遂变得日益准确和可靠[9,10,11]。一般说来,分析的家系数及家系内个体数越多,则对于QTL的检测能力也越强,此时不但检测到的位点数增多,而且每个位点的效应相应变小,不过这些效应在不同遗传背景及环境间的非一致性也会变得愈加明显。此外,为了确保QTL的有效检测和分析,人们对于遗传模型及取样策略的选择也有了更进一步的认知。目前,为了避免模型选择的偏差,贝叶斯法正越来越受到人们的关注和重视。该模型选择法既考虑到了模型本身的不确定性,而且根据后验概率对备择模型作出推断,因而较之常规模型选择法往往更加准确和可靠[12]。由于控制每个性状的QTL数量较多,加上每个QTL的效应微小、可变和不可预测,故目前尚难以同时对多个数量性状进行有效的标记辅助选择(MAS)。就农作物的MAS而言,大体情况也是如此,尽管有些作物群体相对狭窄的遗传基础及较长距离的LD通常更有助于MAS的实施和应用[13]。
近年来,人们在林木中也提出采用关联遗传学(AG)方法以克服数量性状MAS内在的局限性[14]。对于通常具有高核苷酸多态性及短距离LD的林木非结构性群体而言,关联分析不失为行之有效的方法之一。林木复杂性状的遗传解析及标记-性状关联分析可为这类性状的遗传改良提供十分有用的信息。近年来,林木中有关材性、抗病性及耐旱性相关候选基因的SNPs(单核苷酸多态性)分析已有过一些报道[15,16,17]。不过,单个关联位点及其等位变异的表型效应大都较小,很少超过表型方差的5%。然而,这样的结果并不令人感到诧异,与人类[18]、家畜[19]及农作物[20]中采用检测能力更为强大的全基因组关联分析法所观察到的结果相比,二者基本一致。以上结果无疑证实了数量性状的复杂性,同时也使期望利用少数或几个离散位点与性状的关联效应直接达到复杂性状一步改良的可能性受到进一步的质疑。除非MAS能捕捉到目标性状的大多数表型变异,否则还是常规的数量遗传学方法更能有效地加速林木育种进程。
随着近年来基因分型技术的快速发展,人们在此基础上进一步提出并建立了一种新的MAS方法,即基因组选择(GS)法,也称全基因组选择法[21]。就常规的MAS或AG方法而言,通常首先需要通过连锁或关联作图定位QTL,然后借助标记及关联信息进行目标性状的选择或其相关基因的筛选鉴定。而GS法则有所不同,该方法主要着眼于QTL加性遗传效应的预测,无需作预先的定位及关联分析。不过,尽管GS法无需作QTL定位分析,但对于QTL必须要有足够的检测能力,而且能够有效地识别噪声和真实效应。为此,QTL的检测需在一个由数量足够多的个体(数百甚至数千个)所构建的 “训练”群体(即参考群体)中进行。在GS中,首先是采用全基因组标记分型芯片对参考群中的个体进行基因型分析,同时对目标性状作表型鉴定。之后,利用该数据集,并采用适当的方法及取样策略建立预测模型,以避免过度拟合。随后,利用该模型估算候选群体中只有基因型而无表型记录的候选个体的基因组育种值,并以此作为预测指标实现对目标性状的选择。GS的开展和实施通常需要开发出一整套数目庞大并能覆盖整个基因组的分子标记,而且有关的基因组区段预期至少与某些已作基因分型的标记处于连锁不平衡状态。
目前,GS已成为家畜育种领域的研究热点,而在植物育种上,GS的研究也正方兴未艾。在家畜育种中,为了充分了解GS的应用前景,人们利用影响GS预期准确性的多个参数及多种分析程序进行过一系列模拟研究[22-27]。最近,一些学者还相继就GS中的一些重要议题作了进一步的分析和探讨,例如跨种群基因组预测的可靠性[28],纯种杂交性能的基因组选择[29],混合及杂种群体的全基因组选择[30],谱系可跟踪条件下低密度基因分型芯片的利用[31],育种程序中GS不同测试策略的评估[32],以及相较于常规的后裔测定选种法GS法所能实现的额外增益[33]等。此外,还有学者已报道了动物模型GS法的实证结果,明确证实了该方法的理论预期[34,35]。鉴于GS极其诱人的前景,该方法同样引起众多农作物[36,37,38,39]及多年生植物[40]育种工作者的极大关注,尽管目前植物育种领域中尚无该方法的实证报道。
由于GS有望能够增加多年生作物每单位时间的遗传增益并提高其低遗传力性状的选择准确性,因而倍受人们的青睐。GS的准确度主要取决于4个因素:(1)标记与QTL之间的连锁不平衡程度,而这又取决于有效群体大小(Ne)及标记数量;(2)由既有基因型又具有表型数据的个体所构成的训练集(即参考群)的大小,该群体被用于标记效应的估计;(3)所选择性状的遗传力;(4)QTL效应的分布(包括位点数量及效应大小)。以上的前2个参数通常可为育种工作者所控制,而后2者则取决于性状本身[33]。GS能否有效地应用于林木育种,连锁不平衡的程度是极为重要的一个影响因素。有报道指出,由于林木物种的远交习性加之它们尚处于驯化及育种的初期阶段,这不但使其未因驯化瓶颈而遭受多样性的丢失,而且连锁不平衡也大都存在于较短的距离范围内,如杨树及松树的自然群体其LD就仅存在于200 bp的范围之内[41,14]。由于LD程度相对较低,因此,若要对这样的群体进行基因组选择,必须借助数量极为庞大的分子标记才能够达到足够的选择准确度。不过,在基因组选择过程中,可以通过减少Ne以增加标记与QTL之间的LD水平[42]。对于林木高世代育种计划中所常用的优良群体而言,当Ne达到20-100时基本上就能够达到基因组选择所需较高的LD水平[2]。不过,为了确保获得长期的遗传增益,仍需对Ne较大的原始群体进行备份以保持其遗传多样性。
本研究目的旨在评估上述4个重要参数对林木GS预期准确度的影响。首先利用确定性公式分别评估训练集(即参考群)大小(N),性状遗传力( h2),以及QTL数量(NQTL)对5种不同规模选择群体GS预期准确度的影响,而这些候选群体的规模基本上覆盖了林木高世代育种计划中不同大小选择群体的规模。最后,我们还就GS法较之基于最佳线性无偏预测(BLUP)的表型选择法其选择效率随育种周期缩短而增加的变化趋势作了进一步的模拟分析。
1 材料和方法

1.1 确定性方法
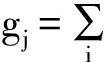
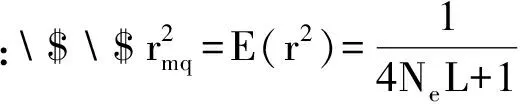
(1)
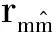

(2)
上该式中bi和P分别为权重及与表型依基因型的回归相关的标记效应的方差。
回归因子与测定基因组育种值的BLUP混合模型方程中的收缩因素密切相关。在混合模型y=Xb+Zm+e下,基因组育种值的预测方程为:

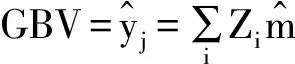
如前所述, r2mq为标记能够解释的所占位点遗传变异(σ2q)的比例,即r2mq=σ2m/σ2q,由此则σ2m=r2mqσ2q。进一步展开公式(2)我们可得出:

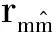
早先,Daetwyler等(2008)[45 ]假定σ2e=1和r2mq=1,于是得出 。
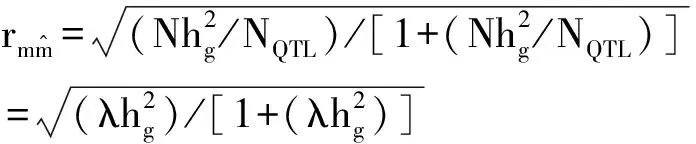
该式无疑显示出参数λ(λ=N/N\%QTL)的重要性,因为λ与训练集中用于估算每个位点效应的表型记录数直接成正比。不过,我们并不作σ2e=1和r2mq=1的假定, 而是保留了更为一般的表达式,所用公式为:

(3)
根据Resende等人(2008)[ 43]的报道,上式中h2m=(h2gr2mq/NQTL)/[h2gr2mq+(1-h2g)] 。我们认为该确定性方法行之有效,正如Meuwissen(2009)[44]已证实的那样,当训练及测评个体因来自同一群体而存在遗传相关时尤其如此。
本研究基于目前或预期可用的林木基因分型技术,分别就以下不同因素对林木基因组选择预期准确性的影响进行模拟分析和评估:
(1)连锁不平衡(LD)水平,即标记所能解释的遗传变异的比例(r2mq)。不同有效群体大小(Ne=10,15,30,60,以及100)及不同标记间隔长度(L=1.0,0.8,0.6,0.5,0.4,0.2,0.1,以及0.05,以厘摩(cM)表示)下的r2mq值可用Sved(1971)[49]的公式(即公式1)计算。以上所提标记间间隔距离的长度可以转变为每厘摩(cM)上标记的数量,分别为每厘摩(cM)上1.0, 1.25, 1.67, 2.0, 2.5, 5.0, 10.0,以及20.0个标记,而这有助于对重组基因组大小不同的物种实施基因组选择所必需的标记总数作出必要的检验。
(2)参考群体(即训练集)中同时具有基因型及表型记录的个体的数量(N=200,500,1 000,2 000,4 000,以及8 000),这是基于林木育种计划中大或较大群体的建立及其表型鉴定通常并不成其为一个限制因子。
(3)性状的遗传力( h2g=0.2,0.3,0.4,0.5,以及0.6),这些性状包括林木育种中常常需要进行遗传力估算的一些重要性状,如材积生长,木材比重,树干通直度,以及木材化学性质等[2]。
(4)QTL的数量(NQTL=1,3,5,10,20,30,50,100,150,以及200)。所有的QTL位点都具有加性效应,而人们在QTL及关联作图中所观察到的与每一性状相关联的标记位点数通常也是介于数个至数十个之间。
1.2 确定性方法的假设
确定性模拟目的旨在利用Sved(1971)[49 ]所提供的方程1计算得到相应模拟条件下的群体平均数。该方程与某一指定长度的染色体区段内不发生交换的概率密切相关。它假定所有这些染色体区段具有一个公共的QTL方差,并且相邻基因组区段间的连锁不平衡仍相互独立。因此,该公式可用于预测整个基因组联合效应的总准确度。不过,尽管如Meuwissen(2009)[44]报道的那样,该公式能够为实施人工选择后的多个世代提供一个合理的近似值,但它可能并不完全适用于预测未来世代的连锁不平衡。 r2mq的最大期望值为1,尽管在某些具体情况下它可能与该E(r2mq)值略有差异。Hill早先(1981)[42]也曾对该问题作过理论探讨,而且之后的一些实验结果[50,51,52,53]进一步证实了该Sved公式的正确性,即便是用小的有效大小群体及不同世代间均如此,这表明随机变异的累积效应应当不是一个主要问题。
BLUP(最佳线性无偏预测)是现今各种动植物育种值估计的有效方法之一,在基因组选择中也可利用该方法实现对标记效应(m)的同步估计和预测。该方法中m被视作随机效应,并服从呈正态的先验分布m~N(0,σ2m) ,在此随机效应框架下得以同时估计出数以千计的标记的效应,即便标记的数量远多于表型记录数。该BLUP法理论上基于无穷小位点模型(每性状受大量乃至无穷多位点控制,而每位点效应甚微),因此单个位点的效应理论上将降低至近乎为零。其它基于贝叶斯框架的方法(如Bayes-B)由于将一些效应值为零的染色体片断考虑在内,因而在有些情况下可能显得更为合理。该方法的可取之处也正是在于许多分离的等位基因其效应几乎可忽略不计。不过有报道指出,BLUP法在GS应用中的效率与更为复杂的贝叶斯法相比并无太大差别[54,55],故本研究采用此方法对林木基因组选择的潜力进行初步评估。
由于BLUP法假定解释遗传方差的所有QTL其效应相等并具有一个公共方差,因此如果对这些QTL的检测效力低下,则所检测到的QTL就只能解释部分的遗传方差,而基因组选择的预期准确性也就相应较低。有鉴于此,在基因组选择中,训练集(参考群体)的样本含量必须大到能够保证足够的检测效力。此外,从Sved公式可以看出,群体的连锁不平衡(LD)水平与有效群体大小及标记间的遗传距离成反比,并与标记密度成正比,故增加样本含量及标记密度将可提高LD水平进而提高GS的准确度,而这有赖于强大的QTL检测效力。 基于以上原因,我们在模拟研究中将训练集(参考群)的最大样本量增加到了8 000个,而在林木育种背景下,对这样大的样本群体进行多个性状的表型分析是完全切实可行的。
1.3 基因组选择法的选择响应
根据定义,选择响应与育种周期的长度成反比。当完成一个育种世代所需的时间减少时,每单位时间的选择响应则相应增加。因此,选择响应(SR,即年遗传进展)可从选择准确度与选择所需总年份之间的比率得知。就基因组选择(GS)而言,SRGS=(rGS)/(CGS),而对于传统基于BLUP的选择法(TS)来说,SRTS=(rTS)/(CTS),这里rGS和rTS分别为GS和TS的选择准确度,CGS和CTS则分别为GS和TS的育种周期长度。进一步计算GS和TS二者选择响应之间的比率即可得知GS相较于TS的选择效率,即RGS:TS=(rGSCTS)/(rTSCGS)。为了计算该选择效率,利用前述的确定性公式(即公式3)可得到GS的准确度。基于表型和系谱信息的传统BLUP选择法的准确度的上界可按Resende及Fernandes(1999)[56]所述REML/BLUP法计算得知。简言之,基于传统BLUP表型选择法的准确度的最大值可由如下公式给出:
(4)$$
为了获得单株BLUP选择最大准确度的估值,我们把N设置到一个很大的数目,同时将公式4中的单株狭义遗传力( h2b)和单株广义遗传力(h2h)分别设定为0.2和0.3,因为在林木全同胞家系试验中生长性状的遗传力估值通常处于这一水平。
利用该公式及以上设定的参数值,我们算出传统BLUP选择法准确度的上限为0.68。当采用轮回选择策略对一般配合力(GCA)进行基因组选择时(这里仅一般配合力最大的个体或其后代被用于下一轮选择),即以该数值作为比较其相对遗传增益的基准。GS选择效率增长的百分率可按(RGS:TS-1)*100%计算,之后还就其随育种周期缩短而变化的趋势作进一步的分析。
2 结果
2.1 基因分型密度对基因组选择准确度的影响
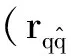
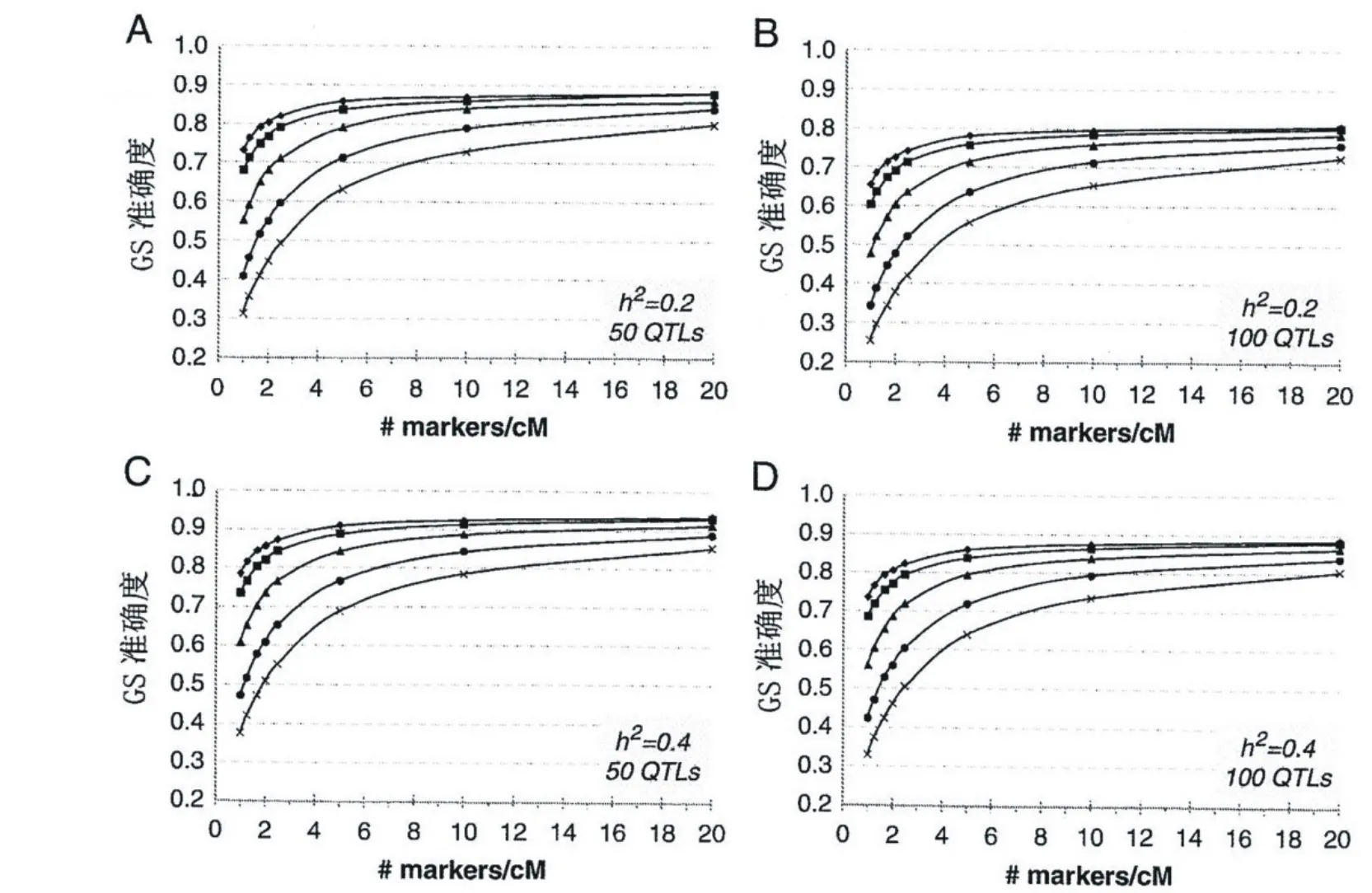
图1 A-D 在狭义遗传力(h2)与控制性状的QTL总数不同组合条件下标记密度(markers/cM)对基因组选择(GS)准确度的影响。训练集大小(N)均设定为1 000。各条曲线分别对应于有效群体大小Ne=10(实心菱形坐标点),Ne=15(实心正方形坐标点),Ne=30(实心三角形坐标点),Ne=60(实心圆形坐标点),以及Ne=100(乘法号坐标点)。
2.2 训练集大小(参考群大小)对基因组选择准确度的影响
分析结果显示,在本研究所设定的有效群体大小范围内,训练集(参考群)大小对基因组选择预期准确度的影响相对较小。在图2所示的4种情形下,当训练集(参考群)中的单株数量超过2 000以后,选择准确度的提高就均已很少。当标记密度较高时,不管所设定的有效群体大小Ne大或小,只要训练集中的单株数量达到1 000,选择准确度即可达到0.8以上。当标记密度较低时,训练集中的单株数量需达到2 000且有效群体大小Ne要小于30才能使GS的选择准确度达到基准值0.68或其以上。
2.3 性状遗传力对基因组选择准确度的影响
分析显示,性状遗传力对基因组选择预期准确度的影响较小。从图3中可以看出,所有绘制出的曲线都非常平直。当遗传力h2从0.2增加到0.6时,不管有效群体大小Ne大或小,基因组选择的准确度仅略增10%~20%。不过,在h2一定的情况下,有效群体大小和标记密度对选择准确度的影响仍然很大,而QTL数量的影响则较小。

图2 A-D 在标记密度(markers/cM)与控制性状的QTL总数不同组合条件下训练集中的个体数量(N)对基因组选择(GS)准确度的影响。狭义遗传力(h2)均设定为0.2。各条曲线分别对应于有效群体大小Ne=10(实心菱形坐标点),Ne=15(实心正方形坐标点),Ne=30(实心三角形坐标点),Ne=60(实心圆形坐标点),以及Ne=100(乘法号坐标点)。
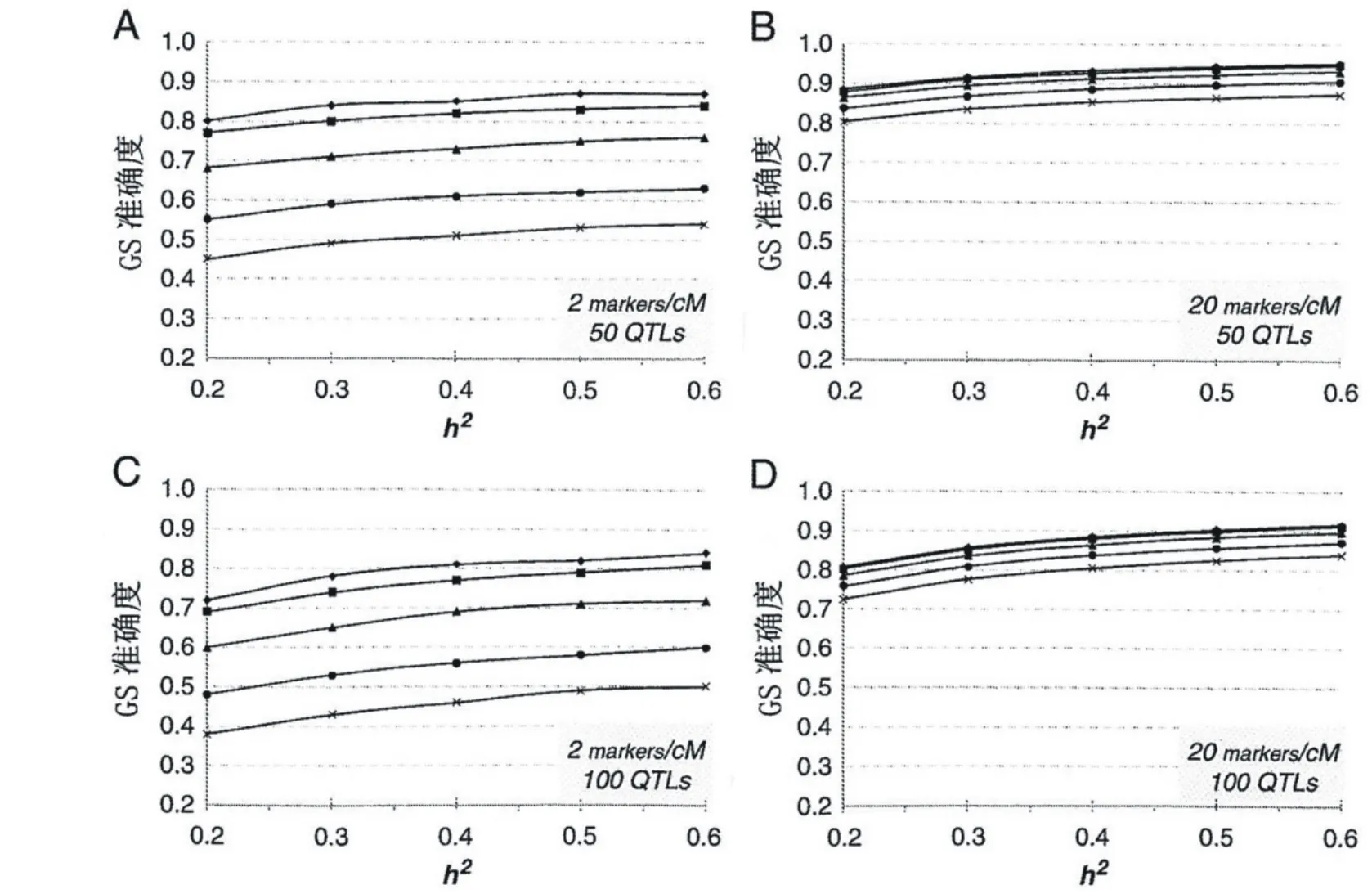
图3 A-D 在标记密度(markers/cM)与控制性状的QTL总数不同组合条件下狭义遗传力(h2)对基因组选择(GS)准确度的影响。训练集中的个体数量(N)均设定为1 000。各条曲线分别对应于有效群体大小Ne=10(实心菱形坐标点),Ne=15(实心正方形坐标点),Ne=30(实心三角形坐标点),Ne=60(实心圆形坐标点),以及Ne=100(乘法号坐标点)。
2.4 QTL数量对基因组选择准确度的影响
当标记密度较低时(2 markers/cM),控制性状的QTL总数(NQTL)对于选择准确度的影响较之标记密度较高时(20 markers/cM)更为明显。在标记密度为20 markers/cM时,随着有效群体大小的增加,选择准确度的变化不大(图4)。当NQTL>150
且遗传力低时(h2=0.2),如果采用较高的标记密度(20 markers/cM),则预期的准确度可达到基准值0.68以上。当控制目标性状的NQTL=100且遗传力h2=0.4时,如果有效群体大小Ne<30,此时即便所采用的标记密度低至2 markers/cM,预期的准确度也可达到0.68或以上。
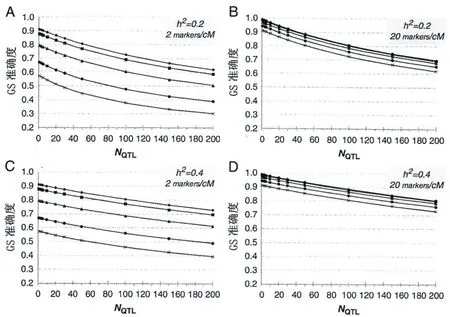
图4 A-D 在狭义遗传力(h2)与标记密度(markers/cM)不同组合条件下控制性状的QTL总数(NQTL)对基因组选择(GS)准确度的影响。训练集中的个体数量(N)均设定为1 000。各条曲线分别对应于有效群体大小Ne=10(实心菱形坐标点),Ne=15(实心正方形坐标点),Ne=30(实心三角形坐标点),Ne=60(实心圆形坐标点),以及Ne=100(乘法号坐标点)
2.5 GS与传统表型BLUP选择法选择效率的比较
相较于传统的表型BLUP选择法, GS选择效率随育种周期缩短而增加的变化趋势见图5。事实上,通过早期对单株实施基因组选择,完全有可能缩短育种周期。该图所模拟的4种情形中,均假定性状遗传力h2=0.2且训练集大小N=1 000,标记密度则设定为2或20 markers/cM,控制性状的QTL设定为50和200。图中X和Y轴交叉点处的0值相应于传统表型BLUP选择法的效率。从图中可以看出,在标记密度低(2 markers/cM)和控制性状的QTL数量为50的情况下,若有效群体大小Ne较小(≤15),则育种周期的长度缩短25%可导致GS选择效率增加约50%(图5a)。不过,当同样情形下但Ne较大或所涉及的QTL数量为200时,育种周期缩短25%并不会导致GS选择效率的实质性增加,甚至比传统表型BLUP选择法的效率更低(沿Y轴的负值)(图5c)。当通过GS使育种周期的长度减少50%时,如果控制性状的QTL数量为50且Ne≤30,则选择效率预期可增加100%以上(图5a)。而当控制目标性状的数量为200时,必须采用较高的标记密度(20 markers/cM)才能使选择效率的增加达到或超过100%(图5d)。如果育种周期的长度能减少75%,此时即便有效群体大小Ne大到100,只要采用较高的标记密度(20 markers/cM),预期的选择效率均可显著增加达300%。在育种周期长度如此强烈减少的情况下,当控制性状的QTL数量为50时,即便标记密度低(2 markers/cM)且有效群体大小Ne=100,此时GS的选择效率依然显著增加达164%(图5a)而在同样条件下,控制性状的QTL数量为200时选择效率仅能增加76%。
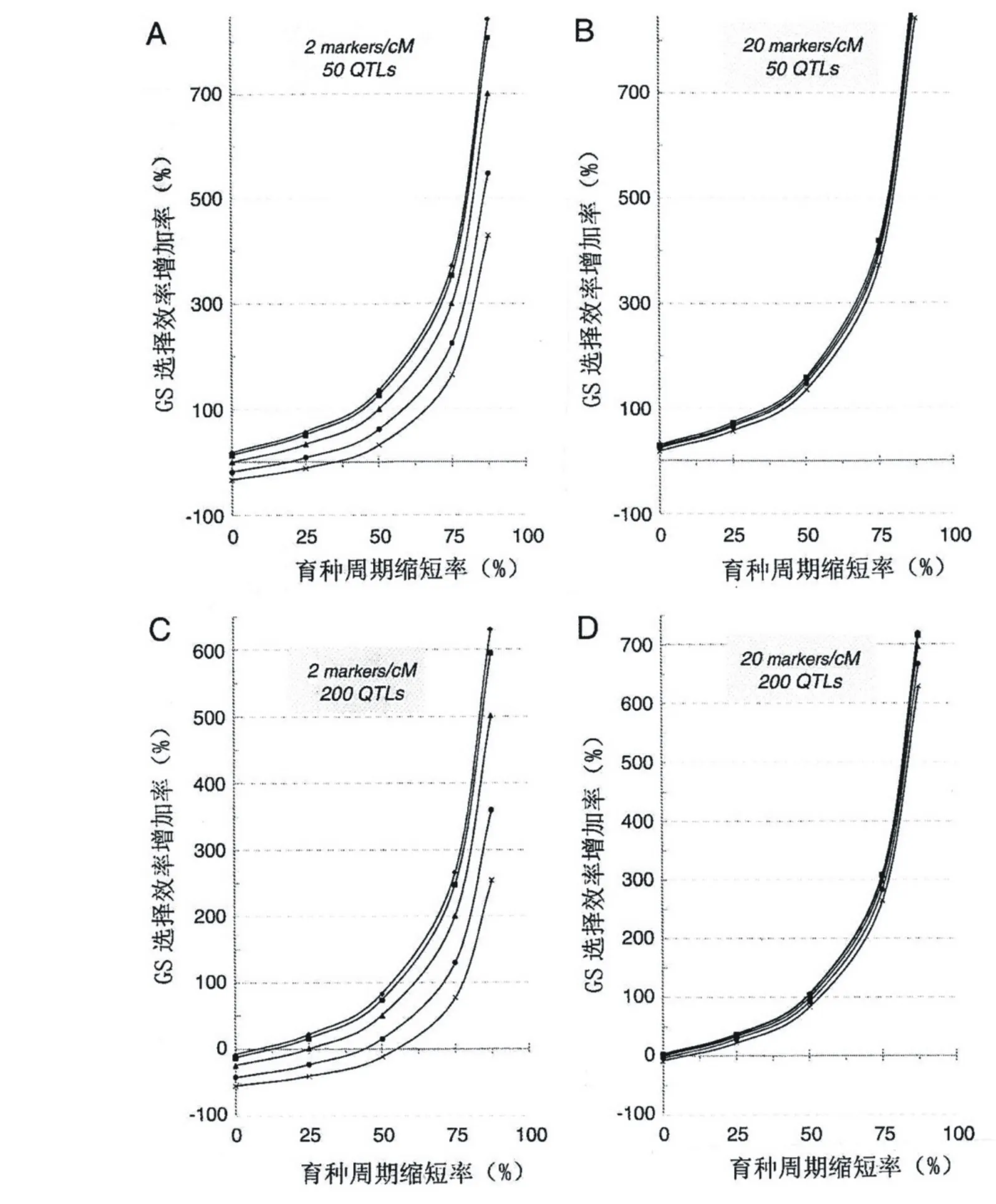
图5 A-D 基因组选择(GS)较之传统的BLUP选择法(TS)其选择效率随育种周期缩短而增加的变化趋势。训练集大小(N)及性状狭义遗传力(h2)均分别设定为1 000和0.2。各条曲线分别对应于有效群体大小Ne=10(实心菱形坐标点),Ne=15(实心正方形坐标点),Ne=30(实心三角形坐标点),Ne=60(实心圆形坐标点),以及Ne=100(乘法号坐标点)。
3 讨论
自Meuwissen等2001[21]年首次提出基因组选择(GS)以来,已有不少人通过模拟研究对影响GS预期表现的一些参数进行过分析评估,同时还就其选择效率与传统的表型选择法进行了比较和探讨[23,48,19,37,57,58,26]。然而,所有这些研究都是针对一些特定的育种对象,其中多数为家畜动物。在此情形下,有效群体大小通常较大且不能加以控制,构成训练群体的个体的可得性可能是GS的一个限制因素[19]。在植物中,已有GS应用于近交的一年生作物如玉米的报道,其所用群体为双单倍体系[36,59],目的为外来种质的快速渗入[60]。就多年生作物而言,迄今为止人们仅在育种周期一般为19年的油棕中对GS的应用前景进行过评估,其结果显示,按照每单位成本和时间获得的遗传增益,GS要优于基于表型的选择法[40]。不过,该研究是在预测测交性能的背景下,从一个单一的F2群体开始并利用一个数量为120-160个的标记集模拟GS。这虽然很有意思,但在林木育种中实际已摒弃这种方案。
我们的研究目的旨在为各种林木植物GS的评估及应用提供有效的参考和依据,而不管其种类,重组基因组大小,以及育种周期的长度。本研究在一系列切合实际的条件下,包括目前可用的基因分型技术及林木高世代育种群体通常的有效群体大小等,对已知影响GS预期准确性的4个主要参数[33]分别进行了评估。结果显示,标记-QTL连锁不平衡(LD)的程度(通过不同的有效群体大小及标记密度进行模拟)对林木GS的应用前景影响最大。当Meuwissen等2001年[21]首次提出GS时也直观地感觉到了这一点,之后Solberg等2008[27]年在评估不同标记类型及密度的效应时使之得到了证实。LD既可因祖先群体中的新突变而先前就存在,也可因遗传漂移而产生新的LD[25]。在林木育种背景下,我们是以新LD产生为前提进行确定性预测。标记与QTL在原始自然群体中被假定处于连锁平衡状态,因育种群体的选择产生遗传漂移进而使这种关联回复到连锁不平衡(LD)状态是成功实施林木GS的一个必要条件。
3.1 基因组选择的准确性主要依赖于有效群体大小及基因分型密度
我们的研究结果表明,只要满足有效群体大小(Ne)和基因分型密度上的一定要求,GS有可能从根本上提高林木育种的速度和效率。我们在整个研究中均以表型BLUP选择法的最大准确度作为GS的基准点,结果显示,只要有效群体大小(Ne)保持在60以下,即便标记密度较低时(大约2-3 markers/cM)GS的效率也能达到该基准值(图1)。目前林木上可利用的基因型分析技术已经能够达到这样的标记密度。在桉属(Eucalyptus)植物中,依据物种及群体遗传结构,DNA差异芯片显示技术(DArT)已能提供大约3 000到5 000个高质量多态性全基因组标记[61]。就一个1 500 cM(厘摩)的基因组[62]而言,这相当于2-3 markers/cM的标记密度。在火炬松(Pinus taeda)中,采用一个大小类似的重组基因组[63],一个具有大约7 000个SNP的SNP芯片可在群体水平上提供大约3 000个有效标记[64]。在云杉(Picea sp.)中同样也开发出了数百个SNPs,而且其中较大部分可有效覆盖略为大一些的重组基因组(估计约3000cM)[65]。
然而,若考虑在有效群体大小(Ne)较大的情况下进行基因组选择,则标记密度需达到10或直到20 markers/cM(图1)。依据育种群体的重组基因组大小及有效群体大小,这样一个靶基因分型密度需开发出能检测大约2 000至≥5 000个标记的基因分型芯片。在杨属(Populus)植物中,由于已有参考基因组序列可用,通过利用新一代测序技术对多个单株基因组的测序及大规模SNP开发,完全有可能开发出这样大的SNPs基因分型芯片。目前,人们已开始为达成这一目标而努力,并且有望很快获得这种大规模的基因分型工具(C.Douglas及G.Tuskan私人通讯)。在桉属(Eucalyptus)植物中,DArT芯片能被快速升级到较大数量的标记。此外,鉴于该属植物的核苷酸多态性高[66,67],故可按杨树中所报道的同样方法,利用即将从巨桉(Eucalyptus grandis)中获得的参考基因组序列开发出大量SNPs[68]。可以预见的是,就基因分型密度而言,对目前普遍采用高世代育种计划的主要林木物种实施GS并不存在技术上的限制。不过,成本将会是考虑的一个主要问题。采用目前通常能提供3 000至5 000个有效标记的DArT基因分型芯片,多态性标记每数据点的成本预计为1至5美分[61]。在提供信息的标记检出数相似时,目前的SNP基因分型成本按一个数据点计略显较高,而当需要20 000个标记时,每样本的成本将增加至数百美元。以如此较高的标记密度实施GS至少需每个样品的成本下降一个数量级。目前,人们在目标富集策略、基因组复杂性降低方法以及与之相结合的多重条形码样品的高通量测序研究上所取得的进展[69,70]有望使育种工作者通过短序列深度测序以很高的密度及显著下降的成本实现单株样品的基因分型,进而使基因分型的成本和效率得到根本性的改变。
3.2 准确的基因组选择需要一个相对大的训练集
我们的研究结果表明,除了育种群体中的LD水平之外,训练集的大小对GS的准确性也有较大影响。我们观察到,当训练集中的个体数N达到1 000时,GS的准确性呈现快速增加,而N超过2 000之后,不论基因分型密度高低及Ne大小,准确性的增加均趋于平稳(图2)。不过,如果QTL的分布违背每个位点效应相等及具有一个共同方差的假定,则并不是所有的遗传方差都能被解释,而且预期的选择准确度也会较低。在此情形下,如果所利用的训练集其大小在2 000个单株以上,则或许可避免这样的模型违例。我们的结果与Goddard等(2009)[19]的模拟研究也相一致,即除非Ne≤100,否则训练集的样本含量需达到数千个体才能准确地预测育种值。我们的研究还显示,在基因分型密度较高的情况下,如果N达到1 000,则无论Ne大或小,GS的选择准确度均能达到甚至超过基准点0.68(即基于BLUP的表型选择法的最大准确度),而当N达到和超过2 000之后,GS的准确度提高甚少(图2)。基于这一结果,我们在评估其它参数的效应时将训练集的大小均设定为1 000。样本含量为1 000个单株的训练集不但可提供令人满意的GS准确度,而且在大多数育种计划中针对这种大规模的样本群体作表型分析鉴定也都应在可行范围内。一般说来,人们很容易对这种规模甚至更大规模群体的生长性状(树高和胸径)进行高精度测定。同样,采用大规模木材质量检测方法[71,72,73,74]也能对数百或数千个样本的各种理化性状进行测定。通过对训练集一些评估困难或测定费用高昂的性状(如耐旱或耐霜性,抗病性,以及生理或生物量相关性状等)的表型分析,GS有可能成为改良这类复杂的多因子性状更强有力的工具。
3.3 遗传力及QTL数量对GS准确度的影响相对较小
本研究中,当训练集的样本植株数均为1 000时,无论设定的有效群体大小大或小,GS准确性随性状遗传力增加而增加的幅度均相对较小(图3)。按前述确定性方法计算所得GS的准确度直接与遗传力和λ的乘积成正比,这里λ为训练集中的表型记录数与所涉及的QTL数量之间的比率,即λ=N/NQTL[45]。图3显示,如果所用的训练集较大(N=1 000),则控制性状的QTL数不管假定为50还是100,遗传力对准确性的影响均相对较小。该结果与Meuwissen等(2001)[21]、Solberg等(2008)[27]以及Nielsen等(2009)[57]的模拟研究也相一致,他们曾指出,因遗传力下降导致的准确度降低很容易通过利用较大的训练集而抵消。Hayes等(2009)[33]对性状遗传力,训练集大小,以及选择准确度之间的关系也进行过评估和分析,结果显示,当对Ne大的群体(Ne=1 000)进行GS时,如果采用GS准确度达到0.6-0.8所必需的表型记录数,则遗传力从0.2增加至0.6其效应增加会下降80%以上。从林木育种角度出发,这些结果表明,如果一个来自Ne≤100的目标群体的训练集相对较大(N≥1 000),即便通过提高该训练集的表型测定质量(如通过无性系重复)以努力提高性状的遗传力,GS准确度的增加也不大。
虽然连锁不平衡值,N,以及h2可根据模拟研究被给予较为切实的建议,但在选择中对于控制性状的QTL数量却难以如此。目前,人们通过林木QTL作图研究已能够了解一些性状QTL数量的下限,而与过去的传统方法相比,该项技术显然有着更为强大的检测效力。例如,Rae等(2008)[11]利用组合毛果杨×美洲黑杨在三个地点从母本和父本中分别鉴定出了37和45个与茎干及生物量性状相关的QTL;同年,Dillen等[10]定位了数十个控制材积生长量的QTL;之后,Novaes等(2009)[75]也定位了63个与20个生长及材质性状相关的QTL。正是基于这些研究,本文报道了控制多个生长及木材质量性状的QTL总数可能为50或100时GS的模拟研究结果。我们的研究还显示,当采用较低的基因分型密度且性状遗传力低时,如果控制性状的QTL数量由100增加至200个,此时即便Ne小至15甚至10,GS的准确度也低于其基准值0.68(即基于BLUP的表型选择法所能达到的最大准确度)。不过,在标记密度较高的情况下,即便Ne大遗传力又低,此时QTL数量的增加对GS准确度的影响并不太大(图4)。假定100个QTL是控制一个目标性状较为符合实际的平均位点数,当育种群体的Ne≤30时,采用2 markers/cM的基因分型密度即可使GS的准确度达到传统BLUP表型选择法的水平。不过,如果控制性状的QTL数达到200个且Ne≤100,则需将基因分型密度提高至20 markers/cM才能达到表型选择法的准确度。
3.4 基因组选择可通过缩短育种周期的长度从根本上提高选择效率
有赖于与GS相关的一系列重要条件(即Ne,基因分型密度,h2,以及NQTL),以及所用确定性方法的相关假定,GS的预期准确度可以赶上或超过基于BLUP的传统表型选择法的水平。从本文图1-4可以看出,在一定条件下,GS的预期准确度均大于基准值0.68,这表明GS这种方法本身可比BLUP表型选择法更加有效。尤为重要的是,通过GS能够实现单株早期选择进而极大程度地缩短育种周期,而这种优势更是为普通的BLUP选择法所难以比拟[21,25]。图5显示,随着完成一个育种周期所需时间的缩短,选择效率呈几何级数增长。考虑到一般配合力的轮回选择,借助GS以缩短林木育种周期值得关注和重视。为了加快育种周期,通过GS选出的单株必须使其开花并经杂交重组得到下一代。开花诱导是目前大多数桉属植物(Eucalyptus)育种程序中的例行步骤之一。通过人工诱导,在热带物种大约12-24个月及温带物种约36-48个月时即可大量开花[76,77],而在自然条件下,这两类植物通常需要4-8年才能开花。同样,在火炬松(P.taeda)中,取自仅3年生种子苗的接穗在嫁接后即可经诱导实现开花[78]。分析结果显示,通过将育种周期长度缩短50%,例如将热带桉树的育种周期从6年缩短到3年,或将温带火炬松的育种周期从16年缩短到8年,选择效率预期可增加100%以上,而在Ne≤30的情况下,即便标记密度较低时GS也能取得这样的效果。如果Ne较大,而且涉及的QTL数甚至达200个,但只要标记密度较高同样也可达到类似的选择效率。设若育种周期的长度可缩短75%,则选择效率更是会快速增加。例如,在基因分型密度高和(或)Ne≤30时,选择效率可增加200%或以上(图5)。然而,由于GS选出的单株必须同时提早开花才能进行杂交并获得下一代,因而育种周期缩短75%实际上难以达到。
3.5 林木基因组选择的机遇与挑战
本研究结果表明,在目前的基因分型技术条件下,通过降低有效群体大小(Ne)产生新的LD是成功实施GS的一个关键因素。然而,Ne下降也存在一种潜在的负面效应,那就是会制约以后世代的选择进展。目前,一些小的优良育种群体已越来越多地被用于获取短期的遗传增益,而较大的群体则作为后备材料以供获取长期遗传进展之需。Ne为20-40的育种群体可支持几个世代的选择并使育种计划获得相当可观的遗传增益[79,2]。例如在美国东南部,火炬松的第3个育种周期已开始采用一个由40个单株构成的经高度选择的群体以期能取得快速的遗传进展[80]。这类高世代的改良群体将最有可能被应用于GS。在桉树中,由20-30个优良亲本构成的群体通常也被用于合成群体间的相互轮回选择,这一改良策略可开发利用来自多个物种的遗传变异,而且无须分别运用多个群体即可选择出结合了多个优良性状(如耐寒或耐旱及生长和材质优异等)的杂种单株[81]。由于每一个多物种群体的Ne 小且LD水平高,因而这样的群体和策略特别适用于GS。
我们的确定性研究建立在相关遗传模型的一系列假定和种群历史基础之上,故在实际育种中未必一定有效。这样,所估计的选择进展可能也就难以实现。例如,我们假定所有QTL都有同等效应,甚至标记和QTL都均衡地分布于整个基因组,但实际上如果某一性状涉及一些效应较大的QTL并且它们以群集方式存在于基因组中,则显然就不符合我们的假定。此外,我们的估算模型还假定不存在显性效应(即仅考虑加性效应),对大多数林木植物而言,这是适合于育种值预测的。不过,当GS是为了将选出的单株用作无性系而不是用作亲本产生下一代时,显性效应的预测对于预测总的遗传值(即育种植)就有很大影响,这时显然应将显性效应加入到模型之中。就理论上而言,这应当不成问题,不过还必须得到进一步的实验验证。总的来说,我们认为本研究有关4个GS评估参数的主要结论具有一定的普遍性,对于林木GS的评估和应用应当具有一定的参考和指导作用。
以上我们还没有谈到GS所面临的一些困难和挑战,而在考虑实施GS之前必须对这些问题有所认识和了解。首先是,对于与训练集(参考群)间隔若干世代的群体基因组预测还会有多高的准确性。在本研究GS的初步评估中,我们仅探讨了在一个世代(即当前世代)中的选择。在经过许多代轮回选择之后,如果因标记与QTL位点之间的重组而使得这些位点不能被有效选择,则这种跨世代预测的有效性必然会迅速下降,这样,训练集将不得不重新取样。不过,也有模拟研究表明,与训练集间隔3代以内每代的预期准确度仅下降约5%,之后下降率还会有所收敛,甚至到第6代下降率也相对不大[21]。还有报道指出,如果标记密度足够高,随着间隔世代数的增加,选择准确度依然不会发生剧烈下降[27]。在目前的林木育种中,即使通过开花诱导世代时间也仍长达2-4年,因此,在力求加快林木育种进程的背景下,即便每6个世代就得重估预测模型也是值得的。此外,还有另外一种策略可供选择,那就是将多基因效应纳入相应的BLUP或贝叶斯模型以使不同世代间能保持持久的标记效应。由于相应的拟合模型可使偏差下降故无而需每一代重估标记效应[27]。
第2个问题是GS在群体或种间相互轮回选择中究竟会有怎样的表现,而在一些林木植物中,种间相互轮回选择业已成为人们常用的一种育种手段。由于不同群体之间标记效应可能会有所不同,因而跨群体或跨物种基因组预测(GS)的一个困难是基因组育种值的估算。不过,最近动物育种中的一些相关研究表明,尽管跨群体及跨物种GS的准确度有可能下降,但依然能够通过GS对纯种的杂交性能作出准确的选择而无需利用谱系或品种信息[28,29,30]。
第3个问题是,犹如Muir早先[25]已指出的那样,与普通的表型BLUP选择法相比,采用GS有可能导致长期遗传进展下降。在动物育种上,已有人针对该问题提出过一些应对措施[48]。林木育种计划的一个共同特点是可同步发展可供维持长期遗传进展的备用群体,而利用这些群体将新的遗传多样性不断引入采用GS的优良群体有望解决这一问题。
第4个问题是,与普通的表型BLUP选择相比,采用GS是否会迅速增加群体的近交程度。Daetwyler等(2007)[82]的研究结果表明,GS不但可使不同性状实现更均衡的选择进展,而且还能大大降低群体的近交率。对于林木植物而言,这无疑会增加其育种计划的可持续性,就这点而论GS也颇受育种工作者的青睐。
最后一个重要问题是,在计划实施GS之前必须仔细考虑GS的基因分型及数据处理成本。随着技术的快速进步及基因分型方法费用的下降,并权衡GS的总成本与每单位时间遗传进展增加的潜力,我们谨慎而乐观地认为,GS在一些林木物种的高世代育种计划种中具有很大的应用潜力。不过,在林木育种中推荐及实施GS之前尚有大量工作需做,包括进一步的模拟研究,本项初步研究中尚未涉及到的一些重要因素和问题的评估,尤为重要的是还要得概念验证试验的相关数据和资料。
[1] Grattapaglia D, Chaparro J, Wilcox P, et al.(1992) Mapping in woody plants with RAPD markers: applications to breeding in forestry and horticulture.Proceedings of the Symposium “Applications of RAPD Technology to Plant Breeding”.Crop Science Society of America, American Society of Horticultural Science, American Genetic Association, pp 37-40
[2] White TL, Adams WT, Neale DB (2007) Forest genetics.CABI, UK
[3] Williams CG, Neale DB (1992) Conifer wood quality and marker-aided selection-a case-study.Can J For Res-Revue Canadienne De Recherche Forestiere 22:1009-1017
[4] Strauss SH, Lande R, Namkoong G (1992) Limitations of molecularmarker-aided selection in forest tree breeding.Can J For Res-Revue Canadienne De Recherche Forestiere 22:1050-1061
[5] Grattapaglia D, Plomion C, Kirst M, et al.(2009) Genomics of growth traits in forest trees.Curr Opin Plant Biol 12:148-156
[6] Kirst M, Myburg A, Sederoff R (2004) Genetic mapping in forest trees: markers, linkage analysis and genomics.Genet Eng (N Y) 26:105-141
[7] Sewell M, Neale D (2000) Mapping quantitative traits in forest trees.In: Jain SM, Minocha SC (eds) Molecular biology of woody plants, vol.1 (Forestry Sciences, Vol 64).Kluwer Academic, The Netherlands, pp 407-423
[8] Beavis WD (1998) QTL analyses: power, precision, and accuracy.In: Patterson AH (ed) Molecular dissection of complex traits.CRC Publishing, Boca Raton, pp 145-162
[9] Brown GR, Bassoni DL, Gill GP, et al.(2003) Identification of quantitative trait loci influencing wood property traits in loblolly pine (Pinus taeda L.).III.QTL Verification and candidate gene mapping.Genetics 164:1537-1546
[10] Dillen S, Storme V, Marron N, et al.(2008) Genomic regions involved in productivity of two interspecific poplar families in Europe.1.Stem height, circumference and volume.Tree Genetics & Genomes 5:147-164
[11] Rae A, Pinel M, Bastien C, et al.(2008) QTL for yield in bioenergy Populus: identifying G × E interactions from growth at three contrasting sites.Tree Genet Genomes 4:97-112
[12] Sillanpaa MJ, Corander J (2002) Model choice in gene mapping: what and why.Trends Genet 18:301-307
[13] Bernardo R (2008) Molecular markers and selection for complex traits in plants: learning from the last 20 years.Crop Sci 48:1649-1664
[14] Neale DB, Savolainen O (2004) Association genetics of complex traits in conifers.Trends Plant Sci 9:325-330
[15] Eckert AJ, Bower AD, Wegrzyn JL, et al.(2009a) Asssociation genetics of coastal douglas fir (Pseudotsuga menziesu var.menziesii, Pinaceae).I.Cold-hardiness related traits.Genetics 182:1289-1302
[16] Gonzalez-Martinez SC, Huber D, Ersoz E, et al.(2008) Association genetics in Pinus taeda L.II.Carbon isotope discrimination.Heredity 101:19-26
[17] Gonzalez-Martinez SC, Wheeler NC, Ersoz E, et al.(2007) Association genetics in Pinus taeda L.I.Wood property traits.Genetics 175:399-409
[18] Visscher PM (2008) Sizing up human height variation.Nat Genet 40:489-490
[19] Goddard ME, Hayes BJ (2009) Mapping genes for complex traits in domestic animals and their use in breeding programmes.Nat Rev Genet 10:381-391
[20] Buckler ES, Holland JB, Bradbury PJ, et al.(2009) The genetic architecture of maize flowering time.Science 325:714-718
[21] Meuwissen TH, Hayes BJ, Goddard ME (2001) Prediction of total genetic value using genome-wide dense marker maps.Genetics157:1819-1829
[22] Calus MP, Meuwissen TH, de Roos AP, et al.(2008) Accuracy of genomic selection using different methods to define haplotypes.Genetics 178:553-561
[23] Dekkers JCM (2007) Prediction of response to marker-assisted and genomic selection using selection index theory.J Anim Breed Genet 124:331-341
[24] Long N, Gianola D, Rosa GJM, et al.(2007) Machine learning classification procedure for selecting SNPs in genomic selection: application to early mortality in broilers.J Anim Breed Genet 124:377-389
[25] Muir WM (2007) Comparison of genomic and traditional BLUPestimated breeding value accuracy and selection response under alternative trait and genomic parameters.J Anim Breed Genet 124:342-355
[26] Schaeffer LR (2006) Strategy for applying genome-wide selection in dairy cattle.J Anim Breed Genet 123:218-223
[27] Solberg TR, Sonesson AK, Woolliams JA, et al.(2008) Genomic selection using different marker types and densities.J Anim Sci 86:2447-2454
[28] de Roos AP, Hayes BJ, Goddard ME (2009) Reliability of genomic predictions across multiple populations.Genetics 183:545-553
[29] Ibanz-Escriche N, Fernando RL, Toosi A, et al.(2009) Genomic selection of purebreds for crossbred performance.Genet Sel Evol 41:12
[30] Toosi A, Fernando RL, Dekkers JC (2009) Genomic selection in admixed and crossbred populations.J Anim Sci 88:32-46
[31] Habier D, Fernando RL, Dekkers JCM (2009) Genomic selection using low-density marker panels.Genetics 182: 343-353
[32] Sonesson AK, Meuwissen THE (2009) Testing strategies for genomic selection in aquaculture breeding programs.Genet Sel Evol41:37
[33] Hayes BJ, Bowman PJ, Chamberlain AJ, et al.(2009) Invited review: genomic selection in dairy cattle: progress and challenges.J Dairy Sci 92:433-443
[34] Lee SH, van der Werf JHJ, Hayes BJ, et al.(2008) Predicting unobserved phenotypes for complex traits from whole-genome SNP Data.Plos Genetics 4
[35] Legarra A, Robert-Granie C, Manfredi E, et al.(2008) Performance of genomic selection in mice.Genetics 180:611-618
[36] Bernardo R, Yu JM (2007) Prospects for genomewide selection for quantitative traits in maize.Crop Sci 47:1082-1090
[37] Heffner EL, Sorrells ME, Jannink JL (2009) Genomic selection for crop improvement.Crop Sci 49:1-12
[38] Zhong SQ, Dekkers JCM, Fernando RL, et al.(2009) Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study.Genetics 182:355-364
[39] Jannink JL, Lorenz AJ, Iwata H (2010) Genomic selection in plant breeding: from theory to practice.Brief Funct Genomics 9:166-177
[40] Wong CK, Bernardo R (2008) Genomewide selection in oil palm: increasing selection gain per unit time and cost with small populations.Theor Appl Genet 116:815-824
[41] Ingvarsson PK (2008) Multilocus patterns of nucleotide polymorphism and the demographic history of Populus tremula.Genetics 180:329-340
[42] Hill WG (1981) Estimation of effective population-size from data on linkage disequilibrium.Genet Res 38:209-216
[43] Resende MDV, Lopes PS, Silva RL, et al.(2008) Sele??o gen?mica ampla (GWS) e maximiza??o da eficiência do melhoramento genético.Pesqui Florestal Bras 56:63-77
[44] Meuwissen THE (2009) Accuracy of breeding values of 'unrelated' individuals predicted by dense SNP genotyping.Genet Sel Evol 41:35
[45] Daetwyler HD, Villanueva B, Woolliams JA (2008) Accuracy of predicting the genetic risk of disease using a genome-wide approach.PLoS ONE 3:e3395
[46] Lynch M, Walsh B (1998) Genetics and analysis of quantitative traits.Sinauer Associates, Sunderland
[47] Mrode RA (2005) Linear models for the prediction of animal breeding values.CABI, UK
[48] Goddard M (2009) Genomic selection: prediction of accuracy and maximisation of long term response.Genetica 136:245-257
[49] Sved JA (1971) Linkage disequilibrium and homozygosity of chromosome segments in finite populations.Theor Popul Biol 2:125-141
[50] Abasht B, Sandford E, Arango J, et al.(2009) Extent and consistency of linkage disequilibrium and identification of DNA markers for production and egg quality traits in commercial layer chicken populations.BMC Genomics 10:S2
[51] Amaral AJ, Megens HJ, Crooijmans RPMA, et al.(2008) Linkage disequilibrium decay and haplotype block structure in the pig.Genetics 179:569-579
[52] Heifetz EM, Fulton JE, O'Sullivan N, et al.(2005) Extent and consistency across generations of linkage disequilibrium in commercial layer chicken breeding populations.Genetics 171:1173-1181
[53] Megens HJ, Crooijmans RPMA, Bastiaansen JWM, et al.(2009) Comparison of linkage disequilibrium and haplotype diversity on macro- and microchromosomes in chicken.BMC Genetics 10:86
[54] Hayes BJ, Goddard ME (2008) Technical note: prediction of breeding values using marker-derived relationship matrices.J Anim Sci 86:2089-2092
[55] VanRaden PM (2008) Efficient methods to compute genomic predictions.J Dairy Sci 91:4414-4423
[56] Resende MDV, Fernandes JSC (1999) Procedimento BLUP (melhor predi??o linear n?o viciada) individual para delineamentos experimentais aplicados ao melhoramento florestal.Revista de Matemática e Estatística (Biometric Brazilian Journal - in Portuguese) 17:89-107
[57] Nielsen HM, Sonesson AK, Yazdi H, et al.(2009) Comparison of accuracy of genome-wide and BLUP breeding value estimates in sib based aquaculture breeding schemes.Aquaculture 289:259-264
[58] Piyasatian N, Fernando RL, Dekkers JCM (2007) Genomic selection for marker-assisted improvement in line crosses.Theor Appl Genet 115:665-674
[59] Mayor PJ, Bernardo R (2009) Genomewide selection and markerassisted recurrent selection in doubled haploid versus F-2 populations.Crop Sci 49:1719-1725
[60] Bernardo R (2009) Genomewide selection for rapid introgression of exotic germplasm in maize.Crop Sci 49:419-425
[61] Sansaloni CP, Petroli CD, Carling J, et al.(2010) A highdensity diversity arrays technology (DArT) microarray for genome-wide genotyping in Eucalyptus.Plant Meth 6:16
[62] Brondani RP, Williams ER, Brondani C, et al.(2006) A microsatellite-based consensus linkage map for species of Eucalyptus and a novel set of 230 microsatellite markers for the genus.BMC Plant Biol 6:20
[63] Sewell MM, Sherman BK, Neale DB (1999) A consensus map for loblolly pine (Pinus taeda L.).I.Construction and integration of individual linkage maps from two outbred three-generation pedigrees.Genetics 151:321-330
[64] Eckert AJ, Pande B, Ersoz ES, et al.(2009b) High-throughput genotyping and mapping of single nucleotide polymorphisms in loblolly pine (Pinus taeda L.).Tree Genet Genomes 5:225-234
[65] Pavy N, Pelgas B, Beauseigle S, et al.(2008) Enhancing genetic mapping of complex genomes through the design of highlymultiplexed SNP arrays: application to the large and unsequenced genomes of white spruce and black spruce.BMC Genomics 9:21
[66] Kulheim C, Yeoh SH, Maintz J, et al.(2009) Comparative SNP diversity among four Eucalyptus species for genes from secondary metabolite biosynthetic pathways.BMC Genomics 10:452
[67] Novaes E, Drost DR, Farmerie WG, et al.(2008) High-throughput gene and SNP discovery in Eucalyptus grandis, an uncharacterized genome.BMC Genomics 9:312
[68] Grattapaglia D, Kirst M (2008) Eucalyptus applied genomics: from gene sequences to breeding tools.New Phytol 179:911-929
[69] Mamanova L, Coffey AJ, Scott CE, et al.(2010) Target-enrichment strategies for next-generation sequencing.Nat Meth 7:111-118
[70] Myles S, Chia JM, Hurwitz B, et al.(2010) Rapid genomic characterization of the genus vitis.Plos One 5:e8219
[71] Raymond CA, Schimleck LR (2002) Development of near infrared reflectance analysis calibrations for estimating genetic parameters for cellulose content in Eucalyptus globulus.Can J For Res- Revue Canadienne De Recherche Forestiere 32:170-176
[72] Robinson AR, Mansfield SD (2009) Rapid analysis of poplar lignin monomer composition by a streamlined thioacidolysis procedure and near-infrared reflectance-based prediction modeling.Plant J 58:706-714
[73] Schimleck LR, Sussenbach E, Leaf G, et al.(2007) Microfibril angle prediction of Pinus taeda wood samples based on tangential face NIR spectra.IAWA J 28:1-12
[74] Tuskan G, West D, Bradshaw HD, et al.(1999) Two high-throughput techniques for determining wood properties as part of a molecular genetics analysis of hybrid poplar and loblolly pine.Appl Biochem Biotechnol 77-9:55-65
[75] Novaes E, Osorio L, Drost DR, et al.(2009) Quantitative genetic analysis of biomass and wood chemistry of Populus under different nitrogen levels.New Phytol 182:878-890
[76] Griffin AR, Whiteman P, Rudge T, et al.(1993) Effect of Paclobutrazol on flower-bud production and vegetative growth in 2 species of eucalyptus.Can J For Res-Revue Canadienne De Recherche Forestiere 23:640-647
[77] Hasan O, Reid JB (1995) Reduction of generation time in eucalyptusglobulus.Plant Growth Regul 17:53-60
[78] Greenwood MS (1980) Method for inducing early flowering on young forest trees.In: Office USPaT (ed).Weyerhaeuser Company, Tacoma
[79] Namkoong G, Kang HC, Brouard JS (1988) Tree breeding: principles and strategies.Springer, New York
[80] McKeand SE, Bridgwater FE (1998) A strategy for the third breeding cycle of loblolly pine in the southeastern US.Silvae Genetica 47:223-234
[81] Resende MDV, de Assis TF (2008) Selecào recorrente recíproca entre populacǒes sintéticas multi-espécies (SRR-PSME) de eucalipto.Pesqui Florestal Bras 57:57-60
[82] Daetwyler HD, Villanueva B, Bijma P, et al.(2007) Inbreeding in genome-wide selection.J Anim Breed Genet 124:369-376
全文译自Tree Genetics & Genomes (2011) 7:241-255
Genomic selection in forest tree breeding Translator
TIAN Lang1, Proofreader LING Qing-gen2
(1.RubberResearchInstitute,ChineseAcademyofTropicalAgriculturalSciences,Danzhou,Hainan571737;2.InstituteofScientificandTechnicalInformation,ChineseAcademyofTropicalAgriculturalSciences,Haikou,Hainan571101)
Genomic selection (GS) involves selection decisions based on genomic breeding values estimated as the sum of the effects of genome-wide markers capturing most quantitative trait loci (QTL) for the target trait(s).GS is revolutionizing breeding practice in domestic animals.The same approach and concepts can be readily applied to forest tree breeding where long generation times and late expressing complex traits are also a challenge.GS in forest trees would have additional advantages: large training populations can be easily assembled and accuratelyphenotyped for several traits, and the extent of linkage disequilibrium (LD) can be high in elite populations with small effective population size (Ne) frequently used in advanced forest tree breeding programs.Deterministic equations were used to assess the impact of LD (modeled by Ne and intermarker distance), the size of the training set, trait heritability, and the number of QTL on the predicted accuracy of GS.Results indicate that GS has the potential to radically improve the efficiency of tree breeding.The benchmark accuracy of conventional BLUP selection is reached by GS even at a marker density ~2 markers/cM when Ne≤30, while up to 20 markers/cM are necessary for larger Ne.Shortening the breeding cycle by 50% with GS provides an increase ≥100% in selection efficiency.With the rapid technological advances and declining costs of genotyping, our cautiously optimistic outlook is that GS has great potential to accelerate tree breeding.However, further simulation studies and proof-of-concept experiments of GS are needed before recommending it for operational implementation.
Genome-wide selection;Effective population size;Linkage disequilibrium;Marker-assisted selection(MAS)
2015-01-18 译者简介:田郎(1961-),男,侗族,湖南新晃侗族自治县人,硕士,副研究员,现从事植物组织培养及分子生物学研究工作。E-mail:tianerlang@163.com。
凌青根(1965-),男,汉族,湖南双峰县人,大学本科,副研究员,现从事科技期刊编辑工作。E-mail: lqgen22@163.com。
Q946.885
A
1001-2117(2015)04-0115-17
