基于2D-PCA特征描述的非负权重邻域嵌入人脸超分辨率重建算法

曹明明 干宗良 崔子冠 李 然 朱秀昌

(南京邮电大学江苏省图像处理与图像通信实验室 南京 210003)

基于2D-PCA特征描述的非负权重邻域嵌入人脸超分辨率重建算法

曹明明 干宗良 崔子冠 李 然 朱秀昌*

(南京邮电大学江苏省图像处理与图像通信实验室 南京 210003)

在基于邻域嵌入人脸图像的超分辨率重建算法中，训练和重建均在特征空间进行，因此，特征选择对算法性能具有较大影响。另外，算法模型对重建权重未加限定，导致负数权重出现而产生过拟合效应，使得重建人脸图像质量衰退。考虑到人脸图像的特征选择以及权重符号限定的重要作用，该文提出一种基于2维主成分分析(2DPCA)特征描述的非负权重邻域嵌入人脸超分辨率重建算法。首先将人脸图像分成若干子块，利用K均值聚类获得图像子块的局部视觉基元，并利用得到的局部视觉基元对图像子块分类。然后，利用2D-PCA对每一类人脸图像子块提取特征，并建立高、低分辨率样本库。最后，在重建过程中使用新的非负权重求解方法求取权重。仿真实验结果表明，相比其他基于邻域嵌入人脸超分辨率重建方法，所提算法可有效提高权重的稳定性，减少过拟合效应，其重建人脸图像具有较好的主客观质量。

图像处理；人脸超分辨率重建；邻域嵌入；局部视觉基元；2维主成分分析

1 引言

近年来，一种专门针对人脸图像的超分辨重建技术成为研究的热点，通常称该技术为“幻觉脸”(face hallucination)[1]。由于人脸图像的特殊性，基于学习的人脸超分辨率重建算法成为研究的主流方向，这类方法主要分为3种：全局脸算法[1,2]、局部脸算法[3−5]、全局脸与局部脸相结合的算法[6,7]。

由于人脸可被看作是一种流形结构，因此基于流形学习的人脸超分辨率重建算法引起了普遍关注。文献[8]首次将流形学习算法引入到图像的超分辨率重建中，提出了邻域嵌入超分辨率(Super Resolution through Neighbor Embedding, SRNE)重建算法，该算法不需要大量的训练样本、复杂度低而得到了广泛的研究[9−14]。考虑到人脸图像的结构相似性，以及位置在重建过程中的作用，文献[15]提出了基于位置的人脸超分辨率重建算法，然而该算法在训练样本数目大于图像子块维数时解不再唯一，一些学者对此做了改进[16,17]。随着压缩感知理论的发展，稀疏描述作为一种新惩罚函数应用到基于流形学习的超分辨率重建算法中[3−5]。文献[4]指出用固定的l1范数作为惩罚函数来提取人脸图像的稀疏特征不能够适应图像内在的统计特性，并提出了一种自适应稀疏权重的算法。基于稀疏描述的算法可以重建出高质量的图像，然而算法复杂度较高，对于大尺寸字典需要训练很长的时间。

本文着重研究基于邻域嵌入算法的人脸图像的超分辨率重建。SRNE算法的训练和重建均在特征空间进行，如何选择图像子块的特征对算法性能具有较大影响。文献[8]选取一阶二阶梯度作为图像子块的特征描述，文献[18]指出二阶梯度受噪声和边缘的影响较大，影响了重建的质量，并提出采用一阶梯度和标准亮度(norm luminance)的结合作为图像子块的特征。考虑到人脸图像的结构特性，采用上述特征并不能较好地保护图像子块的局部几何结构信息。权重用于描述图像子块与其邻近子块在特征空间中的局部线性几何结构关系，直接影响到重建图像的质量，然而，在SRNE算法中，对于权重仅作了和等于1的约束，而对其符号未加约束，导致负数权重出现[13]，使得重建高分辨率图像子块的亮度产生负值，这有悖于亮度值非负的事实，并且过度追求重建误差最小而产生的负数权重也可能使重建的高分辨率重建图像子块与其真实值偏差变大，这种过拟合现象导致重建高分辨率人脸图像质量退化。

考虑到人脸图像的特征选择以及权重符号限定的重要作用，本文提出了一种基于2维主成分分析(2D Principal Component Analysis, 2D-PCA)特征描述的非负权重邻域嵌入人脸超分辨率重建算法。该算法主要包括以下3个方面：(1)采用局部视觉基元[19](Local Visual Primitive, LVP)对人脸图像子块分类，通过分类可将人脸图像中的相似子块分到同一类别，确保了邻域选择的快速准确；(2)采用2维主成分分析[20]提取人脸图像子块特征，该方法可有效保护局部结构信息；(3)提出了一种可确保权重值非负的求解方法，从而避免负数权重对重建图像的影响。仿真实验表明，通过局部视觉基元对人脸图像子块进行分类，可在较短时间内找到目标图像子块的邻近子块，并且对重建质量影响不大。利用2D-PCA提取特征获得的高分辨率人脸图像有效保护了高频细节信息和几何结构信息，并且提出的权重求解算法避免了负数权重导致的过拟合现象，获得较好地图像重建质量。

2 2D-PCA特征描述的非负权重邻域嵌入人脸超分辨率重建算法

本文提出了一种新的基于邻域嵌入人脸超分辨率重建算法，图1给出了本文算法的框架。在邻域嵌入算法中，邻近子块的选取需要遍历整个低分辨率样本库，然而，对于每一个输入图像子块都需要对整个样本库遍历一次会耗费大量的时间。为了减少遍历时间，第2.1节提出了一种分类方法：采用局部视觉基元对训练样本进行分类，选取邻近子块时只需在其所属类别遍历，可以节省遍历时间；邻域嵌入算法的训练过程和重建过程均在特征空间进行，如何选择图像子块的特征对算法性能具有较大影响。考虑到人脸图像的结构特性，第2.2节提出了一种新的特征提取方法：利用2D-PCA提取图像子块特征。该方法能够较好地保护图像子块的局部几何结构信息；最后，为了避免负数权重对重建人脸图像质量的影响，第2.3节提出了一种新的非负权重的求解方法。

2.1 局部视觉基元分类

在SRNE中，每一个输入图像子块选取邻域时都需要遍历整个样本库，这样耗费很多的时间。本文利用局部视觉基元(LVP)对训练样本进行分类，将相似的人脸块分到同一个类别里，选取邻域时只需要遍历图像子块所属类别，这样可以节省很多时间。首先将人脸图像分块{}去直流分量，然后对去直流分量的图像子块k均值聚类xq={}, q表示类别，n表示此类别人脸图像子块的数目，每一类的中心作为LVP值。局部视觉基元是一些结构块，利用LVP将人脸图像子块分类，相当于将结构相似的人脸图像子块分到同一类别，既不影响邻域选取的准确性又可以减少邻域选取的时间。

2.2 2D-PCA特征描述

在人脸超分辨率重建算法中，如何选择图像子块的特征对算法性能具有较大影响。特征的选择主要有两方面标准：一是低分辨率图像子块的特征尽可能多地包含与其相关的信息，这种先验信息可以使邻近块的选取更加准确；二是尽可能地保持高、低分辨率图像子块结构的一致性。考虑到人脸图像结构的特殊性，本文提出一种新的图像子块的特征描述方法：2D-PCA投影法。2D-PCA方法是对传统PCA方法的一种改进，可以直接在2维图像数据矩阵上进行处理，利用2维图像数据矩阵构造图像的协方差矩阵，进而求出协方差矩阵的主元特征向量，然后将2维图像直接投影到主元特征向量上，从而获得图像的特征表示，而不需要将图像数据矩阵转换为1维向量，这样既可以避免庞大的数据计算，又可以更好地保护图像的局部几何结构。因此，本文利用2D-PCA对同一LVP类别的人脸图像子块提取特征，既能保护人脸图像子块的局部几何结构信息，又可以避免噪声以及边缘部分的影响。具体方法如下：

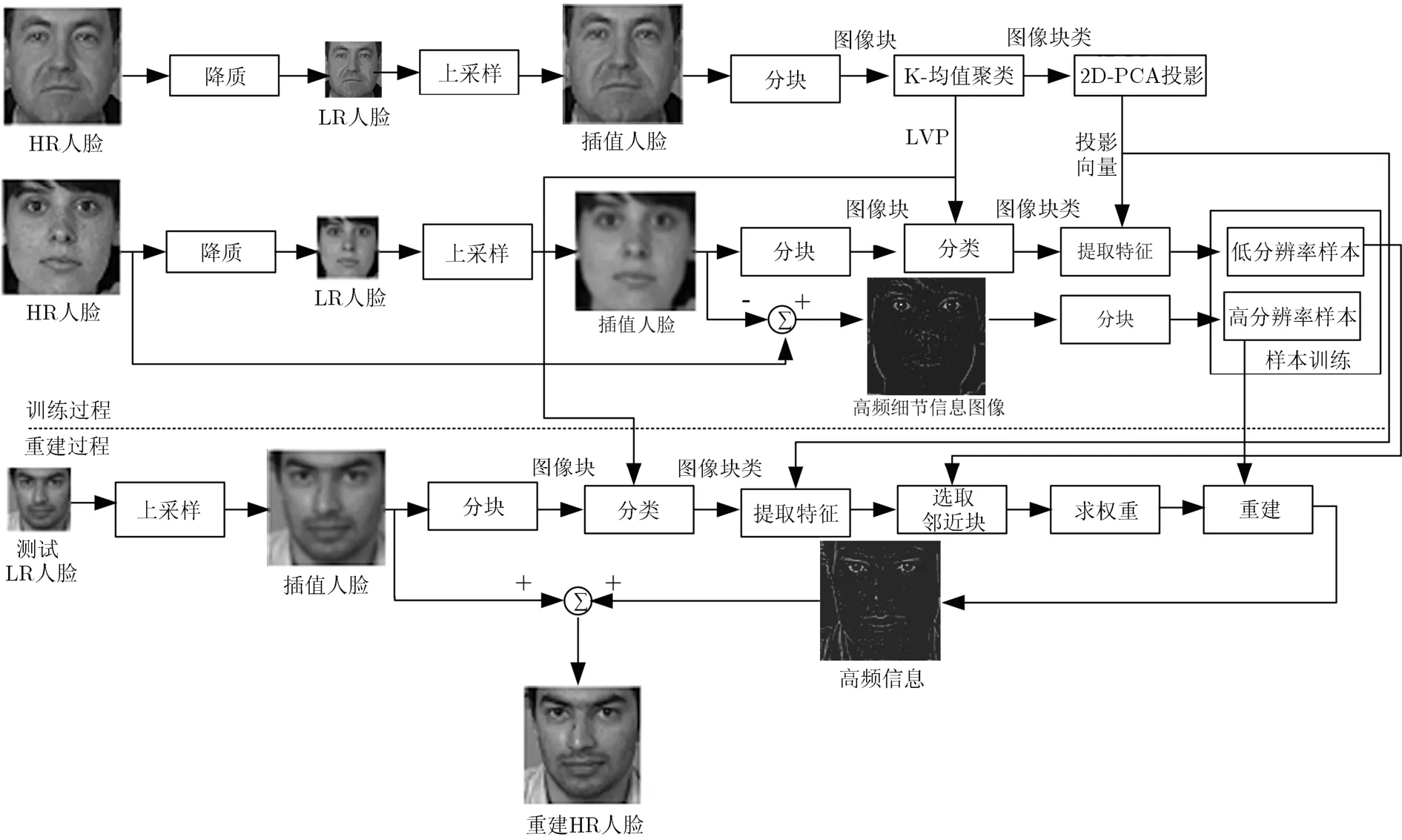
图1 本文算法框架

(1)对于同一类图像子块xq={}，利用式(1)求均值：

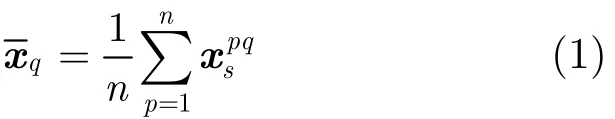
(2)计算相关矩阵Gq：

(3)求相关矩阵的特征值Uq和特征向量Vq。

2.3 非负权重求解

在超分辨率重建算法中数据取负值是没有任何物理意义的，并且数据的混合也只有加性混合。在SRNE中，权重是描述目标图像子块与其邻近块在特征空间中的局部几何关系，直接影响到重建高分辨率图像子块的质量。然而，文献[8]只对权重作了和等于1的约束，对其符号没有限定，在权重的求解过程中会出现权重为负数值的情况。负数权重使得图像子块组合的过程中出现相减的行为有可能产生负的亮度值，这有悖于亮度值非负的事实，并且负数权重也有可能导致过拟合现象，使得重建高分辨率图像质量衰退。文献[13]提出了一种半非负矩阵分解的方法来求取权重，非负矩阵分解的心理学和生理学构造依据是对整体的感知由对组成整体的部分的感知构成的(纯加性的)，更直观地讲就是“将部分组合成一个整体”。因此，为了确保求解的权重不出现负数值本文对其加入非负约束：

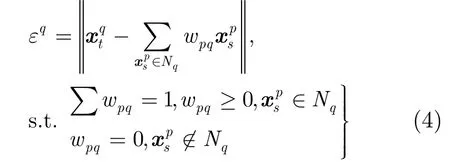
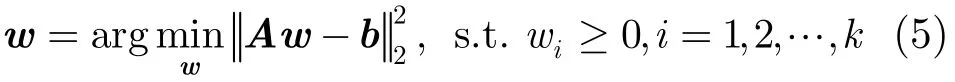
其中

k表示邻近块的数目。

由文献[13]知对于式(5)的非负权重求解问题可以利用半非负矩阵分解算法求解，并且在文献[21]中已经证明了半非负矩阵分解算法在欧式距离目标函数时收敛到局部最优值。然而，在本文算法中，b是已知待重建的低分辨率图像子块的特征形成的矩阵，A是重建子块对应的邻近子块的特征组成矩阵，均为已知量，在迭代求解过程中保持不变，只需要对权重迭代求解，由此可以看出本文算法是非负矩阵分解的一种特例，因此算法求取的非负权重具有局部最优值，并且算法的每一步迭代求解都是在提高(或保持不变)目标图像子块与低分辨率图像样本子块的拟合程度，因此，算法收敛到局部最优值，即求解式(5)的算法可在有限的迭代次数得到最优的非负权重。

3 实验结果与分析

为了验证本文算法对人脸图像的重建效果，本文从人脸图像库中选取了几幅人脸图像进行重建，并与SR[3], ACM[10], LCR[16]的算法以及双立方内插算法进行比较。对于基于邻域嵌入算法人脸图像的超分辨率重建，样本的选择对图像重建的效果有较大的影响，因此，本文从FERET[22]人脸图像数据库里挑选实验图像。

在本文实验过程中，高分辨率人脸图像的尺寸是126×126，并且以两眼连线中心为中心进行图像配准。为了模拟低分辨率图像的获取过程，本文所用到的低分辨率图像通过对高分辨率图像经高斯模糊、双立方插值3倍下采样得到。低分辨率图像的尺寸为42×42。由于与低频信息相比较，中频信息与高频信息更具有相关性，因此，本文先将低分辨率图像采用双立方内插的方法放大3倍，然后再采用本文提出的邻域嵌入超分辨率重建算法进行重建。为了保持子块与子块之间的一致性，相邻两个子块之间重叠几个像素。

3.1 参数设置

很明显，LVP数目不同，得到的类就会不同，每一类所包含的图像子块也会不同。为了了解不同的LVP数目对重建质量的影响，本文设计了仿真实验：在固定其他变量的情况下，LVP数目分别设定为128, 256, 512。表1给出了测试图像在不同LVP取值情况下得到的PSNR和SSIM值的平均值，从数值上可以看出：在LVP数目不同时，重建图像的PSNR和SSIM数值相差不大。从这里可以看出本文提出的局部视觉基元分类对图像重建质量影响不大。在LVP数目增大时，离聚类中心近的块即相似度大的图像子块仍属于同一类别，而仅仅是将距离较远即相似度比较小的图像子块重新划分到别的类别里，属于同一LVP类的图像子块数目减少。这样在选取邻近子块时，不同的LVP数目对邻域的选取影响不大。这恰好证明了本文所提出的局部视觉基元分类的有效性。因为本文算法分类的目的就是在不影响重建图像质量的情况下将训练样本分成若干子样本，在选取邻近块时不必再对整个样本遍历，只需对输入图像子块所属类别的样本库遍历，从而缩短了邻近子块的选取时间。

表1 测试图像在不同LVP取值下的PSNR和SSIM值的平均值

不同的特征描述对于重建图像的质量也有较大的影响。为了验证本文提出的图像子块的特征描述的性能，本文设计了如下对比仿真实验： LVP为256，邻近块数目为5，图像子块的特征分别为一阶二阶梯度和2D-PCA。表2给出了在这两种特征下的重建图像的PSNR和SSIM值的平均值，可以看出采用2D-PCA为特征的重建人脸图像质量要高于一阶二阶阶梯度。图2给出了测试图像的重建人脸图像，从图中可以看出采用2D-PCA和一阶二阶梯度为特征都得到了较好的重建人脸图像，但是在眼角和嘴唇部分采用2D-PCA特征的重建效果明显优于一阶二阶梯度特征，这表明2D-PCA能更好地保存图像子块的局部结构信息。

为了确保在超分辨率重建过程中的权重为非负值，2.3节介绍了一种新的非负权重的求解方法，根据非负矩阵分解的相关理论可以确定此种方法不但可以确保重建权重非负，减少过拟合现象导致的重建人脸图像质量劣化，而且能够保证算法收敛到局部最优值。为了验证提出的非负约束对算法的影响，本文设计了比对试验。图3给出了测试图像在两种不同求解方法(非负权重解和最小二乘解[8])的情况下所得到的重建图像的PSNR, SSIM以及MSE值的比较(此时，LVP=256，采用2D-PCA特征描述)，从图3中可以看出：利用非负权重解算法得到的重建图像的质量要明显优于最小二乘解算法，并且随着邻近块数目的增大非负权重解算法得到的重建图像质量变化相对稳定；同时随着邻近块数目的增加，两种方法都在邻近块数目为5时达到最优值。然而，最小二乘解求解方法得到的重建图像质量在达到最优值后随着邻近块数目的增加下降趋势明显，虽然在邻近块数目为20时PSNR值有所回升，但对应的SSIM值始终减少，利用本文提出的非负权重解求解方法得到的重建图像质量达到最大值后虽有一定程度的下降，但下降趋势较缓且逐渐趋于平稳，这表明非负权重解得到的权重的性能更加稳定，同时也证明了非负约束的合理性和有效性。

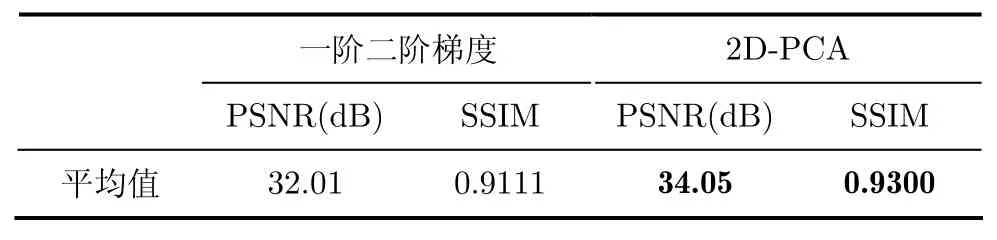
表2 不同特征重建图像的PSNR和SSIM值的平均值

图2 测试图像在不同特征时的重建图像

3.2 实验结果

为了验证本文算法的有效性，本节将提出的算法与其他算法作比较，所有算法使用相同的训练样本(从FERET[22]人脸图像数据库里挑选)，块的大小为3×3。实验得知，图像子块重叠越多，重建质量越好，但重建时间越长。因此，实验过程中所有算法统一重叠1个像素。对于ACM算法[10]本文实验采用一阶二阶梯度特征。表3给出了测试图像在不同算法放大3倍时重建人脸图像的PSNR和SSIM值的比较，从数值上可以看出本文算法要优于其他算法。图4给出了部分重建人脸图，从图中可以看出本文算法的重建人脸图像具有更多的高频细节信息和更合理的局部几何结构。图5给出了不同算法对实际低分辨率人脸图像的重建人脸图，从图中可以看出本文算法在眼睛、嘴角、鼻尖的重建效果要优于其他算法。并且从图中可以看出实测图像中LCR算法的重建效果比较差，是因为LCR算法是基于图像子块位置进行重建，由于本文实验实测图像的配准与FERET人脸图像数据库中人脸图像的配准存在偏差，导致LCR算法在重建过程中，输入图像子块与样本人脸子块的位置存在偏差，导致重建人脸图像质量下降，这也进一步说明本文算法受图像配准的影响比较小。

3.3 算法复杂度分析

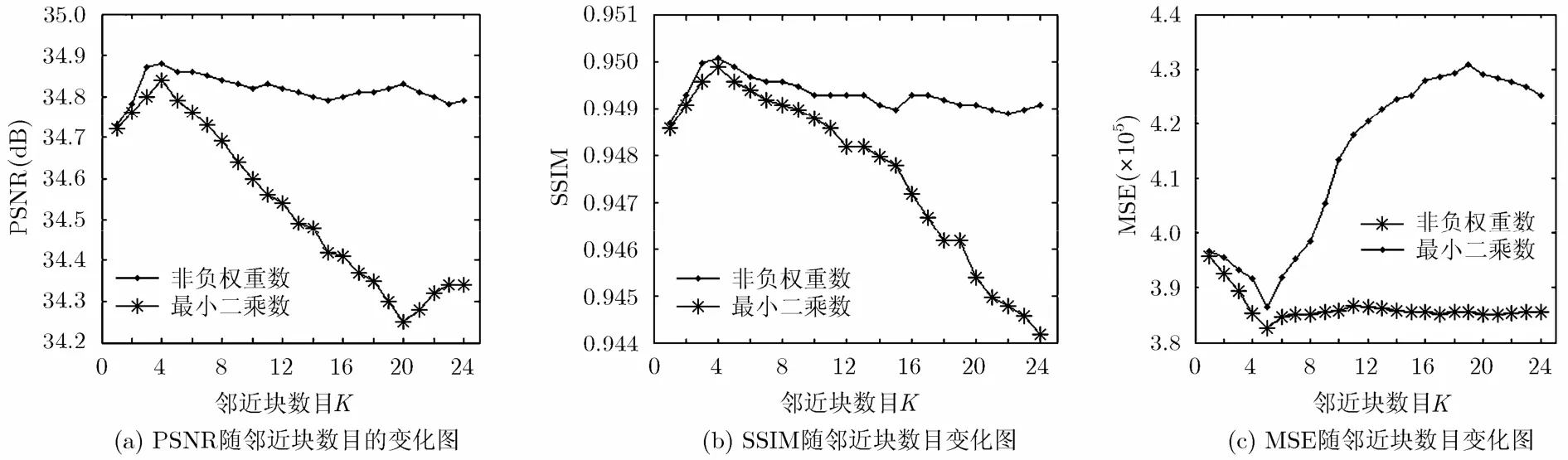
图3 非负权重解和最小二乘解重建图像质量比较

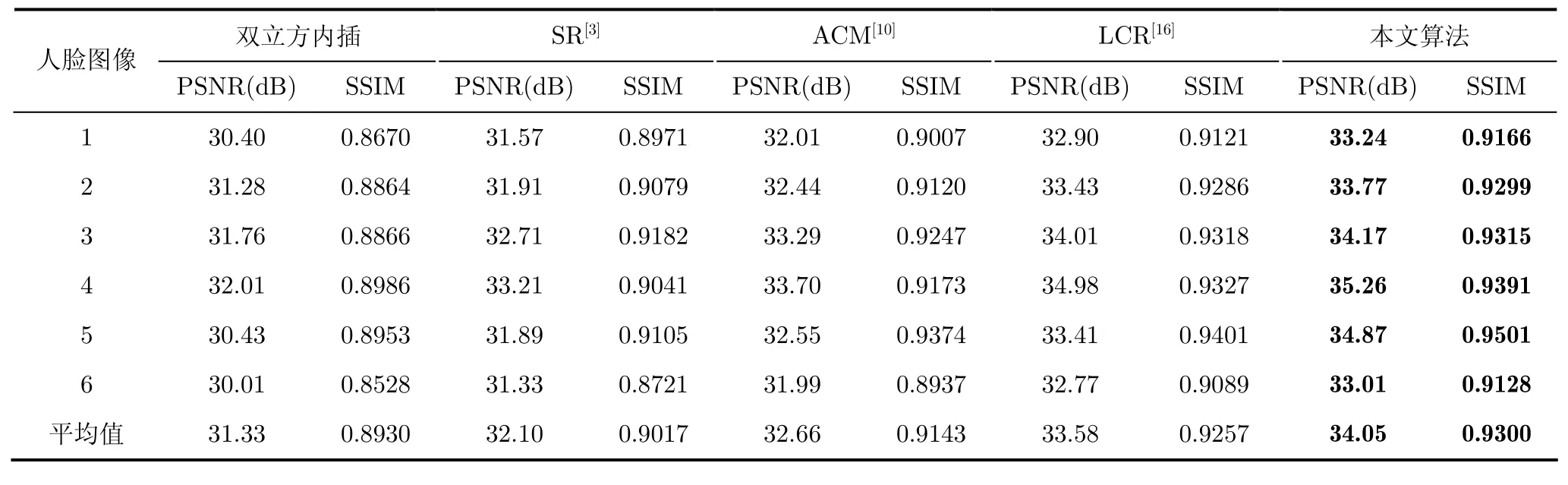
表3 不同算法重构图像PSNR和SSIM比较

图4 不同算法下的人脸图像重建效果图

图5 不同算法对实际低分辨率人脸图像重建效果图

本文算法分成训练过程和重建过程，虽然训练过程花费很多时间，但可以预先对样本进行训练，而在重建过程只需找到输入人脸子块对应的局部视觉基元类，并在此类中求取邻近子块后重建出高分辨率人脸子块，减少了遍历时间，降低了算法复杂度。设实验中样本数目为N，测试人脸图像分成M个大小为p×p的子块。那么在SRNE中重建过程需要计算(p×p×4)×1维特征向量间的欧式距离O(M·N)次。本文算法重建过程的特征向量为(p×p)×1维，首先需要计算O(KLVP)次(KLVP表示LVP数目)找到输入图像子块所属类别，然后在此类里找对应的邻近子块，需计算O(NLVP)次(NLVP表示LVP类样本数)，因此共需要计算O(M·NLVP)次。实验中本文训练样本为1×105，以测试图像5为例：寻找输入块LVP类别计算了1.2×105次欧式距离，求取邻近子块为4.02×105次，总共5.22×105次，而SRNE需计算4.84×107次欧式距离，本文算法计算次数只占SRNE的10.9%，节省了约9倍的重建时间。

4 结论

本文提出了一种基于2D-PCA特征描述的非负权重邻域嵌入人脸超分辨率重建算法。为了减少邻近子块选取过程的遍历时间，本文算法将人脸图像分成若干子块，利用K均值聚类获得图像子块的局部视觉基元，并利用得到的局部视觉基元对图像子块分类。考虑到不同LVP数目对图像子块分类的影响，本文讨论了3种不同的LVP数目对重建人脸图像质量的影响。同时，验证了利用2D-PCA对每一类人脸图像子块提取特征要优于一阶二阶梯度特征。最后，为了避免负数权重对重建人脸图像质量的影响，本文算法在重建过程中使用新的非负权重求解方法求取权重。实验结果表明本文算法可有效提高权重的稳定性，减少过拟合效应，并且重建人脸图像具有较好的主客观质量。

[1] Baker S and Kanade T. Limits on super resolution and how to break them[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1167-1183.

[2] Wang Xiao-gang and Tang Xiao-ou. Hallucinating face by eigentransformation[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2005, 35(3): 425-434.

[3] Yang Jian-chao, Wright J, Huang T S, et al.. Image super resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[4] Wang Zhong-yuan, Jiang Jun-jun, Xiong Zi-xiang, et al.. Facehallucination via weighted sparse representation[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, 2013: 2198-2201.

[5] Wang Zhong-yuan, Wang Shi-zheng, Xia Yang, et al.. Face hallucination based on stepwise sparse reconstruction [C]. IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, 2013, DOI: 10.1109/ICME. 2013. 6607470.

[6] Naleer Haju Mohamed M, Yao Lu, and Feng Lü. Effective two-step method for face hallucination based on sparse compensation on over-complete patches[J]. IET Image Processing, 2013, 7(6): 624-632.

[7] Liu Ce, Shum Heung-yeung, and Zhang Chang-shui. A two step approach to hallucinating faces: global parametric model and local nonparametric model[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, Hawaii, USA, 2001: 192-198.

[8] Chang Hong, Yeung Dit-yan, and Xiong Yi-min. Super resolution through neighbor embedding[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington DC, USA, 2004: 275-282.

[9] Jiang Jun-jun, Hu Rui-min, Han Zhen, et al.. Locality constraint iterative neighbor embedding for face hallucination[C]. IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, 2013, DOI: 10. 1109/ICME. 2013. 6607455.

[10] Li Bo, Chang Hong, Shan Shi-guang, et al.. Aligning coupled manifolds for face hallucination[J]. IEEE Signal Processing Letters, 2009, 16(11): 957-960.

[11] Chen Xiao-xuan and Qi Chun. Low rank neighbor embedding for single image super resolution[J]. IEEE Signal Processing Letters, 2014, 21(1): 79-82.

[12] Jiang Jun-jun, Hu Rui-min, Chen Liang, et al.. Coupled layer neighbor embedding for surveillance face hallucination[C]. IEEE International Conference on Image Processing (ICIP), Melbourne, VIC, 2013: 2802-2806.

[13] Bevilacqua M, Roumy A, Guillemot C, et al.. Neighbor embedding based single image super resolution using seminonnegative matrix factorization[C]. IEEE International conference on Acoustics, Speech and Signal Processing (ICASSP 2012), Kyoto, 2012: 1289-1292.

[14] Hao Yuan-hong and Qi Chun. Face hallucination based on modified neighbor embedding and global smoothness constraint[J]. IEEE Signal Processing Letters, 2014, 21(10): 1187-1191.

[15] Ma Xiang, Zhang Jun-ping, and Qi Chun. Hallucinating face by position-patch[J]. Pattern Recognition, 2010, 43(6): 2224-2236.

[16] Jiang Jun-jun, Hu Rui-min, Han Zhen, et al.. Position patch based face hallucination via locality constrained representation[C]. IEEE International Conference on Multimedia and Expo (ICME), Melbourne, VIC, 2012: 212-217.

[17] Shi Jin-gang and Qi Chun. Face hallucination based on PCA dictionary pairs [C]. IEEE International Conference on Image Processing (ICIP), Melbourne, VIC, 2013: 933-937.

[18] Chan Tak-ming, Zhang Jun-ping, Pu Jian, et al.. Neighbor embedding based super resolution algorithm through edge detection and feature selection[J]. Pattern Recognition Letters, 2009, 30(5): 494-502.

[19] Meng Xin, Shan Shi-guang, Chen Xi-lin, et al.. Local visual primitives (LVP) for face modeling and recognition[C]. 18th International Conference on Pattern Recognition, ICPR2006, Hong Kong, 2006(2): 536-539.

[20] Yang Jian, Zhang D, Frangi A F, et al.. Two-dimensional PCA: a new approach to appearance based face representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137.

[21] Ding C, Li Tao, and Jordan M I. Convex and seminonnegative matrix factorizations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 45-55.

[22] Phillips P J, Hyeonjoon Moon, Rizvi S A, et al.. The FERET evaluation methodology for face-recognition algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(10): 1090-1104.

曹明明： 男，1983年生，博士生，研究方向为图像处理与多媒体通信.

干宗良： 男，1979年生，副教授，研究方向为分布式视频编码、图像(视频)信号处理.

崔子冠： 男，1982年生，讲师，研究方向为视频编码.

李 然： 男，1988年生，博士生，研究方向为图像处理与多媒体通信.

朱秀昌： 男，1947年生，教授，博士生导师，长期从事图像通信方面的科研和教学工作.

Novel Neighbor Embedding Face Hallucination Based on Non-negative Weights and 2D-PCA Feature

Cao Ming-ming Gan Zong-liang Cui Zi-guan Li Ran Zhu Xiu-chang
(Image Processing and Image Communication Key Laboratory, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)

In neighbor embedding based face hallucination, the training and reconstruction processes are performed in the feature space, thus the feature selection is important. In addition, there is no constraint specified for the signs of the weights generated in neighbor embedding algorithm, which leads to over-fitting and degradation of the recovered face images. Considering the importance of feature selection and the constraints of weights, a novel neighbor embedding face hallucination method is proposed based on non-negative weights and Two-Dimensional Principal Component Analysis (2D-PCA) features. First, the face images are partitioned into patches, and the local visual primitives are obtained by k-means clustering algorithm. The face image patches are classified with the local visual primitives generated before. Second, the feature of face image patches is captured with 2D-PCA, and the low and high dictionary is established. Finally, a novel non-negative weights solution method is used to obtain the weights. The experiment results show that the weights computed by the proposed method have more stable behavior and obviously less over-fitting phenomenon, furthermore, the recovery face images have better subjective and objective quality.

Image processing; Face hallucination; Neighbor embedding; Local visual primitives; Two-Dimensional Principal Component Analysis (2D-PCA)

TN911.73

： A

：1009-5896(2015)04-0777-07

10.11999/JEIT140739

2014-06-03 收到，2014-11-18改回

国家自然科学基金(61071091, 61071166, 60802021)，江苏省研究生培养创新工程(CXZZ12_0470)，江苏省自然科学青年基金(BK20130867)， 江苏省高校自然科学研究项目(12KJB510019)和南京邮电大学校科研基金(NY212015)资助课题

*通信作者：朱秀昌 zhuxc@njupt.edu.cn