扫描模式下海杂波的多分形布朗运动模型

孙 康金 钢王超宇马超伟钱卫平高梅国

①(北京跟踪与通信技术研究所 北京 100094)

②(北京理工大学信息与电子学院 北京 100081)

③(中国空气动力研究与发展中心 绵阳 621000)

④(电子科技大学自动化工程学院 成都 611731)

⑤(南京理工大学电子工程与光电技术学院 南京 210094)

扫描模式下海杂波的多分形布朗运动模型

孙 康*①②金 钢③④王超宇⑤马超伟①②钱卫平①高梅国②

①(北京跟踪与通信技术研究所 北京 100094)

②(北京理工大学信息与电子学院 北京 100081)

③(中国空气动力研究与发展中心 绵阳 621000)

④(电子科技大学自动化工程学院 成都 611731)

⑤(南京理工大学电子工程与光电技术学院 南京 210094)

为了提高航海雷达目标检测性能，该文主要研究多分形布朗运动在扫描模式下雷达海杂波分形建模中的应用。该文验证实测海杂波数据具有非对称和尖峰厚尾的非高斯统计分布，并且具有分形特性；同时也证实实测数据在一定的情况下满足多分形布朗运动的假设条件。在此基础上，利用多分形布朗运动对实测数据进行建模，计算得到随时间变化的Hölder函数，结果显示不同距离区域的Hölder指数是不同的，目标处的Hölder指数大于海杂波处的Hölder指数。该文研究结果对后续目标检测方法的提出具有很大的帮助作用。

目标检测；海杂波；分形；多分形布朗运动；Hölder指数

1 引言

分数布朗运动(Fractional Brownian Motion, FBM)是一种自相似过程，对描述许多情况下出现的不规则信号具有很大的帮助。分数布朗运动模型已被大量用于海杂波特性分析和目标检测中。文献[1]以分数布朗运动作为数学模型描述雷达回波信号，提取出海杂波和目标回波的多种分形参数，并利用其固有的差异进行海上目标检测，取得了较好的检测效果。文献[2]比较了海杂波与分数布朗运动的特征，得出海杂波与分数布朗运动具有相似的增量统计特性。与传统相干处理和分形变分法相比，基于FBM模型的分形方法能得到较好的处理结果。文献[3,4]引入分数布朗运动模型对S波段雷达实测海杂波数据进行了计算分析，证实了S波段雷达海面回波信号具有混沌分形特性，并在此基础上提出了海杂波预测方法和海杂波背景下目标检测方法。文献[5]对比分析了高频雷达实测海杂波数据、分数布朗运动模型和多重分形模型的质量指数函数和奇异指数。文献[6]以海杂波分数布朗运动模型为基础，初步解释交叉标度现象出现的机理～，提出基于标度特性差异的目标检测算法。文献[710]对海杂波频域和分数阶傅里叶变换(FRactional Fourier Transform, FRFT)域的分形特性进行了分析研究，证实了海杂波在频域和FRFT域上满足统计自相似条件，具有分形特性，并且提出了相应的目标检测方法。文献[11]将分段分数布朗运动引入到雷达海杂波分形建模中，从频域角度对海杂波频谱进行分段描述。

然而，分数布朗运动模型要求在整个轨迹上的不规则特征是处处相同的。例如，当FBM模型用于人工合成山脉地形时，假设前提是山脉地形的每一部分的不规则程度都是相同的。而实际由于侵蚀等因素的影响，自然中的山脉地形每一部分的粗糙度都是不同的，显然假设条件与实际情况并不相符合。为了克服上述存在的局限，文献[12,13]相继独立提出了多分形布朗运动(multifractional Brownian motion, mBm)。该模型的参数H是一个随时间t变化的连续的β-Hölderian函数，满足0＜inftH(t)≤suptH(t )＜min(1,β)。

目前，关于海杂波分形特性分析和目标检测方法的相关研究主要是针对高分辨雷达进行的，并且不论是驻留模式还是扫描模式，使用的实测海杂波数据反映的都是同一片海域不同时刻经海面反射雷达所接受到的回波信号，可以用一个时间的函数表示。而现阶段使用的航海雷达所接受到的视频信号表现为既是时间又是空间的函数形式。特别地，在雷达扫描线上的海面回波强度是空间距离的函数，并且由于采样点数较少，限制了常用的分形方法在该情况下的研究和应用。本文的主要工作是引入多分形布朗运动作为描述扫描模式下的雷达海杂波的数学模型。本文首先介绍了多分形布朗运动的概念及参数估计，然后从实际的观测数据入手，分析了海杂波的统计特性和分形特性，最后利用多分形布朗运动对海杂波进行分析建模。

2 多分形布朗运动

设(X,dX)和(Y,dY)是两个度量空间。如果对任意x,y∈X，存在β＞0，使得当dX(x,y)＜1，有

则称函数f:X→Y是具有指数β的Hölder函数。

设H:[0,∞)→(0,1)是具有指数β＞0的Hölder函数，如果一个随机过程BH(t)(t)对于t≥0，满足则称随机过程是简化的多分形布朗运动，其中W是一个标准布朗运动。依概率1, BH(t)(t)是t∈[0,∞)的连续函数。

对任意t≥0, 0＜H(t)＜min(1,β)，如果存在唯一的一个连续正值函数tσt，使得随机过程连续，且具有性质为

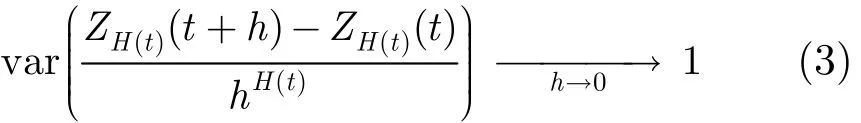
则称该随机过程为标准多分形布朗运动。

当H(t)=H, t≥0，多分形布朗运动和分数布朗运动是等价的；对任意t≥0，多分形布朗运动是近似自相似的，即

由此可以看出，多分形布朗运动是分数布朗运动的一种拓广。因此，从某种意义上来说，多分形布朗运动损失了分数布朗运动本身原有的一些性质：mBm的增量过程实际上是非平稳的，mBm不再是自相似的。但是mBm的假设条件(即H是一个Hölder函数)细化了mBm的连续性。

设{Xi,n,i=1,2,…,n −1}是mBm的离散形式，其在局部上(即适当长度为δ的窗内)表现为给定Hölder指数的分数布朗运动。于是，对部分K∈ℝ+和H(·)∈(0,1]，可得到

其中j=i−δ,i−δ+1,…,i−q , i =δ+1,δ+2,…,n, q=1,2,…,δ。

基于此假设条件，文献[14]在前人基础上提出多分形过程的记忆函数的估计方法，得到一类H(t)的参数估计量，其表达式为

3 扫描模式下的海杂波分形特性分析

本文使用的海杂波数据是某船载导航雷达在航海过程中实时采集得到的，数据采集的范围是以舰船为中心，半径为10 km内的海域。雷达发射信号脉冲重复频率PRF为1300 Hz，接收机采样率为60 MHz。雷达扫描一圈用时2.4 s，接收得到的一圈回波数据有大约3120条数据线，每条数据线约有4000个采样点。图1是某一圈扫描采集到的雷达回波图像。图2是图1中某一条扫描线上的海面回波幅度值。从图2中可以看出，在近距离处，入射到海面的雷达信号强度大，后向散射的回波信号强度也大。从近距离处到远距离处，回波信号的强度逐渐减弱。

3.1 海杂波的统计特性分析

通过计算实测数据的概率密度函数，得到其概率分布，其中某条扫描线实测数据的计算结果如图3中实线所示。图3中点划线和虚线分别表示的是瑞利分布和与实测数据具有相同均值和方差的正态分布，可以看出，实测数据的分布函数与瑞利分布比较相近，而与正态分布不相符合；实测数据的分布不具有对称性，有较长的拖尾，表明实测数据在时域上具有尖峰特性。

偏度γ1是衡量随机变量对称性的一个概率特征，刻画了统计数据分布偏斜方向和程度。如果γ1＞0，意味概率密度函数右侧的尾部比左侧的长，分布的主体集中在左侧，称随机变量具有正偏态分布；如果γ1＜0，意味概率密度函数左侧的尾部比右侧的长，分布的主体集中在右侧，称随机变量具有负偏态分布；如果γ1=0，表示数值相对均匀地分布在平均值的两侧，称随机变量为对称分布。正态分布属于对称分布。而峰度γ2是衡量随机变量峰态的一个概率特征，刻画了统计数据分布集中和分散的程度。如果γ2＞3，称随机变量服从尖峰态分布；如果γ2＜3，称随机变量服从低峰态分布。正态分布的峰度为3。通过计算实测数据得到，γ1=3.63, γ2=16.82。因此，实测数据具有非对称性(正偏态分布)和尖峰特性(尖峰态分布)，故实测数据是非高斯的，与图3的结论相符。

3.2 海杂波的长程相关特性分析

对数方差-时间图法是判断待测数据是否具有长程相关性的一种方法，利用该方法得到海杂波实测数据的log2var(xm)～log2m曲线，其中某条扫描线实测数据的计算结果如图4所示，其中虚线表示的是斜率为−1的曲线。如果曲线的斜率大于−1，则被考察的信号序列具有长程相关性。显然，实测数据的平均斜率大于−1，因此考察的海杂波数据具有长程相关性。

3.3 海杂波的分形特性分析

利用基于数学形态学和小波的两种分形估计方法对海杂波距离向实测数据进行分析[15,16]。图5和图6分别是两种方法的计算结果。从图中可以看出，基于数学形态学的方法计算得到的log2(Ag(ε)/ε2)～log2(1/ε)曲线的斜率几乎为1，而基于小波的方法计算得到的log2Γ(j)和分辨率j的曲线也近似于一条直线。从上面两幅图中的曲线特征，可以得出海杂波实测数据具有分形特性。

图1 某一圈扫描采集到的雷达回波图像

图2 某一条扫描线上的海面回波幅度值

图3 海杂波实测数据的概率分布函数拟合

图4 海杂波实测数据的log2var(xm)～log2m 曲线

图5 海杂波实测数据的log2(Ag(ε) /ε2)～log2(1/ε)曲线

图6 海杂波实测数据的 log2Γ(j)～j 曲线

4 海杂波的多分形布朗运动建模

图7是不同q值下的实测数据增量的概率分布，利用正态分布曲线对实测数据的概率分布曲线进行拟合，拟合误差结果如图8所示。从图7和图8中可以看出，当q=1时，海杂波的概率分布与正态分布存在较大差别；当q=5时，两者的差别有所减小；当q=50时，海杂波的概率分布与正态分布近乎重合；当q=100时，两者的差别稍微有所增加。因此，在q的特定取值范围内，式(5)的假设对本文使用的实测数据是成立的。

(1)远距离区域和近距离区域回波信号的Hölder指数的分析：从图2中可以看出，随着距离由远及近，海杂波强度的变化是不一样的。将整个回波数据分成近距离区域数据和远距离区域数据。根据第2节的参数估计方法，取δ=30, q=10, k=2，计算远、近距离区域的海杂波实测数据的逐点Hölder指数，结果如图9所示。图9(a)和图9(b)分别是近距离区域和远距离区域海杂波数据的幅度波形和Hölder指数，从计算结果中可以得到：第一，对于近距离区域，Hölder指数小于某一数值，在本例中为0.6；第二，对于远距离区域，Hölder指数也小于某一数值，在本例中为0.3。因此，近距离区域和远距离区域的Hölder指数是不一样的，前者的变化范围要大于后者的变化范围。分析认为，海杂波可以看作是较大起伏表面叠加了一些快速变化的小起伏。当观测区域较近时，由于离雷达距离近，散射点分布丰富。某些散射点虽然相互间存在着细微的变化，但是它们处于同一个大的起伏表面，所在的区域具有一定的平滑作用，使得散射点回波不规则程度相对较弱，此时的Hölder指数较大；另一些散射点除了相互间具有细微变化，而且它们分别处于不同的起伏表面，散射点回波不规则程度较强，此时的 Hölder指数较小，所以，近距离区域存在较大范围的Hölder指数变化；当观测区域较远时，信号的分形特征主要由相距较远的散射点之间的关系决定，同一起伏表面的平滑作用逐渐消失，散射点回波不规则程度较强，因此，远距离区域的Hölder指数变化范围较小。

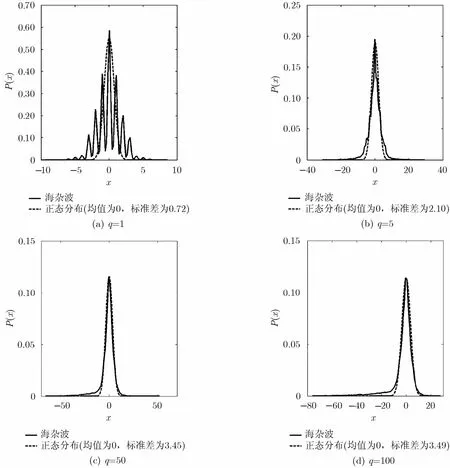
图7 不同q值下的实测数据增量的概率分布

图8 不同q值下的拟合误差

图9 海杂波实测数据的幅度波形和对应的Hölder指数

(2)有目标和无目标回波信号的Hölder指数的分析： 图10是第9圈含有目标的扫描数据线的幅度波形和Hölder指数。从图中可以得到：第一，近距离区域，目标处的Hölder指数大于某一数值，在本例中为0.6；第二，远距离区域，目标处的Hölder指数也大于某一数值，在本例中为0.3；第三，无论是近距离区域，还是远距离区域，相同区域内目标处的Hölder指数值大于同一区域内杂波处的Hölder指数值，即。原因分析为，相对于海杂波，目标表面光滑，散射点分布较均匀且差别很小，后向散射的回波强度变化微弱且缓慢，故Hölder指数较大；而由于海面起伏，散射点分布不均匀，海杂波具有较强的复杂性和不规则性，故Hölder指数较小。分形维数D与Hölder指数H有如下关系，即D=2−H，因此，海杂波处的分形维数值大于目标处的分形维数值，这与前人的研究结果是一致的。

5 结束语

图10 第9圈某扫描数据线的幅度波形和对应的Hölder指数

本文介绍了多分形布朗运动及其参数估计，运用统计和分形的计算方法，对扫描模式下的实测海杂波数据进行了判定，证实了此种情况下的海杂波具有非对称和尖峰厚尾的非高斯统计特性，同时也具有分形特性。本文利用多分形布朗运动对实测数据进行建模，计算了随时间变化的Hölder函数。研究发现：(1)近距离区域和远距离区域的海杂波实测数据的逐点Hölder指数是不同的，而且前者的变化范围要大于后者的变化范围。(2)目标处的Hölder指数和海杂波处的Hölder指数存在较大差别，前者的Hölder指数值大于后者的Hölder指数值。该研究结果将有助于对海上目标进行有效检测，后续将对海上目标检测方法和参数设置等问题做进一步的研究。

[1] Du G. Detection of sea-surface radar targets based on fractal model[J]. Electronics Letters, 2004, 40(14): 906-907.

[2] 王红光, 康士峰, 张忠治. 海杂波的分数布朗运动模型及其应用[J]. 现代雷达, 2005, 27(11): 58-62.

Wang Hong-guang, Kang Shi-feng, and Zhang Zhong-zhi. Fractional Brownian motion model of sea clutter and its application[J]. Modern Radar, 2005, 27(11): 58-62.

[3] 姜斌, 王宏强, 付耀文, 等. 基于LS-SVM的海杂波混沌预测[J]. 自然科学进展, 2007, 17(3): 415-420.

Jiang Bin, Wang Hong-qiang, Fu Yao-wen, et al.. Sea clutter chaotic prediction based on LS-SVM[J]. Progress in Natural Science, 2007, 17(3): 415-420.

[4] 姜斌, 王宏强, 黎湘, 等. S波段雷达实测海杂波混沌分形特性分析[J]. 电子与信息学报, 2007, 29(8): 1809-1812.

Jiang Bin, Wang Hong-qiang, Li Xiang, et al.. The analysis of chaos and fractal characteristic based on the observed sea clutter of S-band radar[J]. Journal of Electronics & Information Technology, 2007, 29(8): 1809-1812.

[5] 盛文, 任吉. 高频雷达海杂波的多重分形建模方法研究[J]. 电波科学学报, 2011, 26(5): 984-989.

Sheng Wen and Ren Ji. Multifractal modeling method for HF radar sea clutter[J]. Chinese Journal of Radio Science, 2011, 26(5): 984-989.

[6] 丁昊, 王国庆, 包中华, 等. DFA在海杂波标度特性分析及目标检测中的应用[J]. 信号处理, 2013, 29(7): 830-837.

Ding Hao, Wang Guo-qing, Bao Zhong-hua, et al.. Application of DFA to scaling property analysis of sea clutter and target detection[J]. Journal of Signal Processing, 2013, 29(7): 830-837.

[7] 刘宁波, 关键, 王国庆, 等. 基于海杂波FRFT谱多尺度Hurst指数的目标检测方法[J]. 电子学报, 2013, 41(9): 1847-1853.

Liu Ning-bo, Guan Jian, Wang Guo-qing, et al.. Target detection within sea clutter based on multi-scale hurst exponent in FRFT domain[J]. Acta Electronica Sinica, 2013, 41(9): 1847-1853.

[8] 宋杰, 刘宁波, 王国庆, 等. 海杂波FRFT谱的近似分形特性与目标检测[J]. 宇航学报, 2013, 34(10): 1394-1402.

Song Jie, Liu Ning-bo, Wang Guo-qing, et al.. Approximate fractality of sea clutter FRFT spectrum and target detection[J]. Journal of Astronautics, 2013, 34(10): 1394-1402.

[9] 刘宁波, 关键, 黄勇, 等. 基于频域多尺度Hurst指数的海杂波中目标检测方法[J]. 电子学报, 2013, 41(3): 424-431.

Liu Ning-bo, Guan Jian, Huang Yong, et al.. Target detection within sea clutter based on multi-scale hurst exponent in frequency domain[J]. Acta Electronica Sinica, 2013, 41(3): 424-431.

[10] 刘宁波, 关键, 宋杰, 等 海杂波频谱的多重分形特性分析[J].中国科学: 信息科学, 2013, 43(6): 768-783.

Liu Ning-bo, Guan Jian, Song Jie, et al.. Multifractal property of sea clutter frequency spectrum[J]. SCIENCE CHINA Information Sciences, 2013, 43(6): 768-783.

[11] 刘宁波, 关键, 黄勇, 等. 海杂波的分段分数布朗运动模型[J].物理学报, 2012, 61(19): 190503.

Liu Ning-bo, Guan Jian, Huang Yong, et al.. Piecewise fractional Brownian motion for modeling sea clutter[J]. Acta Physica Sinica, 2012, 61(19): 190503.

[12] Peltier R F and Véhel J L. Multifractional Brownian motion: definition and preliminary results[R]. INRIA Research Report No.2645, France: Rocquencourt, 1995.

[13] Roux D, Jaffard S, and Benassi A. Elliptic Gaussian random processes[J]. Revista Matemática Iberoamericana, 1997, 13(1): 19-90.

[14] Bianchi S. Pathwise identification of the memory function of multifractional Brownian motion with application to finance[J]. International Journal of Theoretical and Applied Finance, 2005, 8(2): 255-281.

[15] Maragos P and Sun F K. Measuring the fractal dimension of signals: morphological covers and iterative optimization[J]. IEEE Transactions on Signal Processing, 1993, 41(1): 108-121.

[16] Hu Jing, Gao Jian-bo, Posner F L, et al.. Target detection within sea clutter: a comparative study by fractal scaling analyses[J]. Fractals, 2006, 14(3): 187-204.

孙 康： 男，1985年生，博士后，研究方向为宽带雷达信号处理、雷达海上目标探测.

金 钢： 男，1958年生，研究员，研究方向为信息与信号处理、光学工程.

王超宇： 男，1985年生，博士生，研究方向为压缩感知雷达目标成像.

Modeling Sea Clutter in Radar Scanning Mode by Multifractional Brownian Motion

Sun Kang①②Jin Gang③④Wang Chao-yu⑤Ma Chao-wei①②Qian Wei-ping①Gao Mei-guo②

①(Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)

②(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

③(China Aerodynamics Research and Development Center, Mianyang 621000, China)

④(School of Automation, University of Electronic Science and Technology of China, Chengdu 611731, China)

⑤(School of Electronic Engineering and Optoelectronic Technology, Nanjing University of Science and Technology, Nanjing 210094, China)

To improve the detection performance of marine radar, the application of multifractional Brownian motion to modeling the radar sea clutter in the scanning mode is studied. It is verified that real sea clutter data submit to a non-Gaussian distribution with asymmetry, high peak and heavy tail, and have fractal characteristics. In some cases the assumption of multifractional Brownian motion for the real data is satisfied. On the basis of this analysis, the real data are modeled by using the multifractional Brownian motion, and the time-dependent Hölder function of the real data is calculated. The results show that the Hölder exponents of different regions are not the same, and the Hölder exponent of target is significantly larger than that of the sea clutter. The research results are helpful to design a reliable detection method.

Target detection; Sea clutter; Fractal; Multifractional Brownian motion; Hölder exponent

TN959.72

： A

：1009-5896(2015)04-0982-07

10.11999/JEIT140730

2014-05-29收到，2014-09-03改回

*通信作者：孙康 sunkang_me@163.com