跳频周期和跳频间隔的最大条件熵射频隐身设计方法

杨宇晓汪 飞周建江*康国华

①(南京航空航天大学航天学院 南京 210016)

②(雷达成像与微波光子技术教育部重点实验室 南京 210016)

跳频周期和跳频间隔的最大条件熵射频隐身设计方法

杨宇晓①②汪 飞②周建江*②康国华①

①(南京航空航天大学航天学院 南京 210016)

②(雷达成像与微波光子技术教育部重点实验室 南京 210016)

为提高跳频通信系统的被截获性能，该文以跳频周期和跳频间隔为研究对象，提出一种基于最大条件熵的跳频周期、跳频间隔射频隐身联合设计方法。该方法以跳频系统先验数据为样本空间，以拉格朗日乘子为优化粒子，利用混合混沌粒子群优化(HCPSO)算法对最大条件熵的对偶规划进行优化计算。与单阈值方法(STM)和双阈值方法(DTM)的对比仿真结果表明：该文提出的最大熵方法(MEM)具有最大的跳频周期、跳频间隔不确定性和最小的截获概率，且针对不同威胁因子具有较高的环境区分度。因此，MEM具有较好的射频隐身性能，可以有效提高搭载平台的生存能力。

跳频通信；射频隐身；跳频周期；跳频间隔；混合混沌粒子群优化算法

1 引言

近年来，随着雷达等相关技术的发展，无源探测系统对主动射频辐射源的探测能力已大大提高，对载有多种主动辐射源的飞行器平台(飞机、卫星等)构成了严重威胁。射频隐身技术是近年来提出的一种新的隐身技术，主要用以对抗无源探测系统。该技术通过对主动辐射源进行特征控制，有效避免其被无源电子侦察设备截获、分选识别和定位[1−3]。

最大信号不确定性策略是实现射频隐身的重要手段，该策略要求系统辐射信号的频域、时域和空域信号参数不确定性最大，以使敌方侦察设备无法预估，提高其抗分选识别能力。近年来，国内外学者对利用信号不确定性策略降低通信系统截获概率展开了许多研究，跳频系统由于实现简便，针对信号频率特征的不确定研究开展较早。1974年，Lempel和Greenbeger给出了单个跳频序列最大周期汉明自相关理论界(Lempel-Greenbeger界)[4]，在跳频序列理论界的约束下，文献[5,6]提出构造具有最优最大汉明相关值的跳频序列的一般化构造方法。在时域特征不确定研究方面，文献[7]提出利用最大熵方法对猝发通信系统的发射时刻进行优化，使其具有最大不确定性。文献[8]针对流星余迹通信体制完全随机的时域猝发特性，讨论了流星余迹通信的差错控制方式，在其低截获性能的基础上，提高通信质量。在空域特征不确定研究方面，文献[9]提出利用空间天线阵列仅在期望的用户方向上生成信号数据，并随机选取信道进行天线加权发射信号。文献[10]则分析了跳空技术在相控阵天线阵列上的实现方法，并研究了天线阵元位置对跳空能力的影响。

跳频通信与定频通信相比，具有隐蔽性好，抗干扰能力强等优点[11−13]，但跳频系统的跳频周期多为固定值，跳频间隔多为最小间隔的整数倍，敌对侦察方仍可通过跳频频率集、跳频速率及跳频网属等特征参数估计，实现跳频信号截获及分选。因此，为降低跳频系统截获概率，本文以最大信号不确定性为原则，以跳频周期和跳频间隔为研究对象，提出了一种基于最大条件熵的跳频周期、跳频间隔射频隐身联合设计方法，该方法根据不同的战场环境信息，对跳频周期、跳频间隔进行自适应规划，使其熵值为符合约束条件的最大值，即具有符合约束条件的最大不确定性。

2 最大条件熵原理

信息熵是信息论中用来衡量不确定性的数学度量。随机分布的不确定性越高，熵值就越大。1957年Jaynes在信息熵基础上提出了求解非适定问题的最大熵原理(Principle of Maximum Entropy, PME)[14]：在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布。

若在已知条件概念类Xc的条件下，衡量目标概念类Yc和Zc所具有的联合不确定性，则需要用联合条件熵H(Yc,Zc|Xc)来度量，最大熵原理也同样适用于联合条件熵模型，最合理的系统状态应当是符合约束条件且条件熵值最大的状态。联合最大条件熵如式(1)所示。

对于XcYcZc空间中的约束特征(xci,yci,zci)，定义其特征函数，如式(2)所示。

3 截获概率

主动辐射信号的射频隐身性能可以用截获概率来衡量，截获概率可以定义为在采集到的信号序列中处理出主动辐射信号的比率，截获概率是表征主动辐射信号被截获可能性的度量[15]。文献[15]给出的截获概率计算公式为

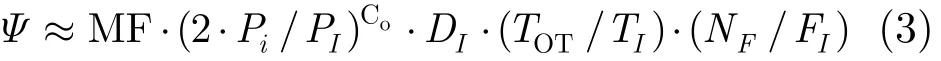
其中，MF为主瓣3 dB波束覆盖面积，Pi为截获接收机收到的功率，PI为截获接收机检测门限，DI为截获接收机密度，TOT为辐射信号驻留时间，TI为截获接收机扫描时间，NF为辐射频率次数，FI为截获接收机扫描频率带宽，CO为覆盖区/灵敏度比例因数。

4 跳频周期、跳频间隔射频隐身联合设计方法

本文提出的基于最大条件熵的跳频周期和跳频间隔射频隐身联合设计方法，以态势感知设备获取的威胁因子为条件类X，跳频周期为目标类Y，跳频间隔为目标类Z，按照最大信号不确定性策略要求，跳频系统应在符合约束条件的基础上，使Y和 Z在X条件下的联合不确定性最大，即Y和Z的联合条件熵H(Y,Z|X)最大，此时跳频系统的射频隐身性能最好。该设计方法主要包含以下3个部分。

4.1 构建拉格朗日函数

本文所要解决的主要问题是在考虑战场环境信

息(即威胁因子)的条件下，使跳频周期和跳频间隔的不确定性最大(即H(Y,Z|X)最大)，因此，可将其考虑为有约束条件的非线性规划类问题。本文所需求解的条件熵H(Y,Z|X)极大值即为非线性目标函数，而威胁因子约束条件则通过XcYcZc空间中不同特征值所具有的不同p(xci,yci,zci),p(xci)和p(yci, zci|xci)来体现的，由于xci,yci,zci相互独立，由概率论原理可得

p(xci,yci,zci),p(xci)和p(yci,zci|xci)分别为XcYcZc空间中取值为(xci,yci,zci)时的联合概率密度函数，xci的概率密度函数和yci,zci在xci下的条件概率密度函数。联立式(1)、式(2)和式(4)，可得求解条件熵H(Y,Z|X)极大值问题的有约束条件的非线性规划，如式(5)所示。

有约束条件的非线性规划问题若满足约束条件为等式约束，则可用拉格朗日乘子法将其转化为无约束条件问题求解。式(5)满足约束条件为等式要求，因此，可将其转化为无约束条件极值问题，并为每个特征函数引入一个参数αi(拉格朗日乘子)，同时为每个x引入参数β(x)，构建拉格朗日函数如下：将式(6)中L(α,p)对p(y,z|x)求导，并令，则使L(α,p)取最大值的条件概率密度模型为

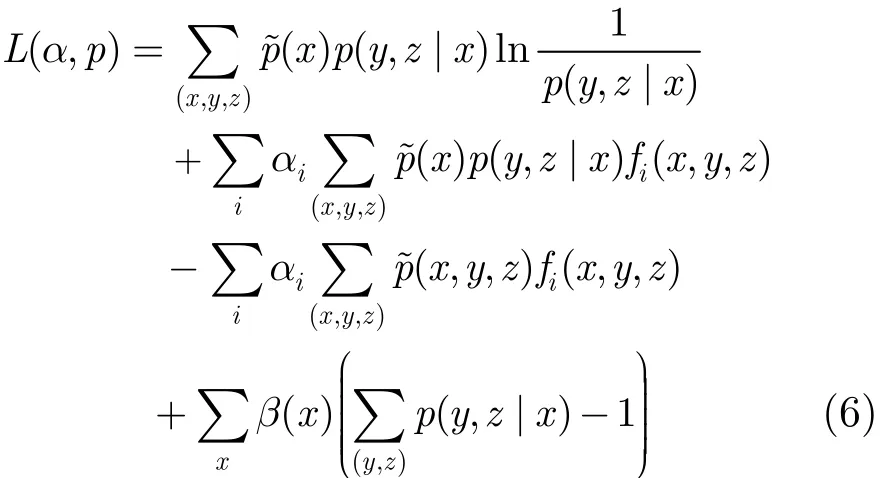
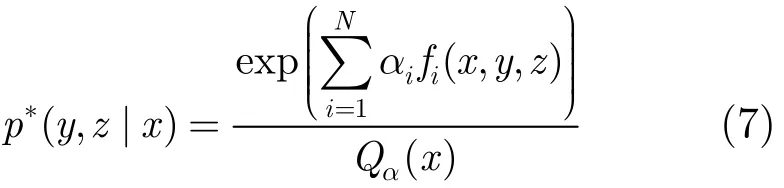
式(7)中Q(x)α为归一化因子。

4.2 确定拉格朗日乘子

为实现联合条件熵H(Y,Z|X)最大，其关键在于确定最优的条件概率密度函数p∗(y,z|x )，由式(7)可知，p∗(y,z|x )可由拉格朗日乘子αi唯一确定，因此，本节将对拉格朗日乘子的求解问题进行讨论。

由于凹函数H(Y,Z |X)极大值的非线性规划可考虑为凸规划问题，根据数学规划中的对偶理论，其应存在相应的对偶规划，即

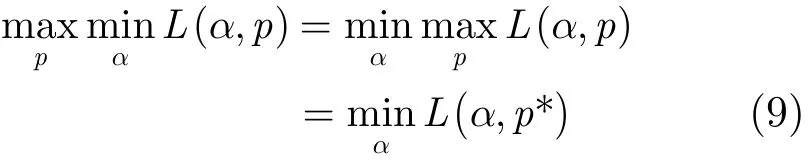
将p∗(y,z|x)代入式(4)中，记为E(α)，则E(α)即为最大条件熵问题的对偶规划：

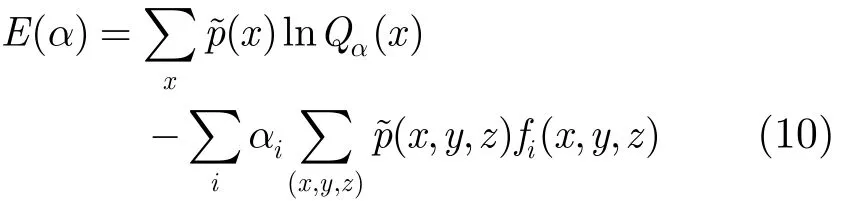
即

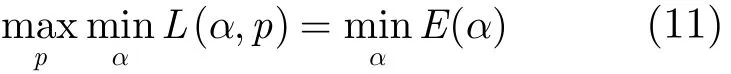
本文采用混合混沌粒子群算法(Hybrid Chaotic Particle Swarm Optimization, HCPSO)[16−18]对E(α)进行优化。以mαinE(α)为目标函数，将式(10)中的拉格朗日乘子α1,α2,…,αN作为N个优化粒子，进行迭代计算，选取使目标函数E(α)最小的一组解作为最优解。将最优解，代入式(7)、式(8)中，即可确定符合约束条件且熵值最大的最大条件熵概率分布模型p∗(y,z|x )。

4.3 符合最大条件熵要求的跳频周期、跳频间隔规划

为提高跳频通信系统的态势感知能力和射频隐身性能，需在考虑战场环境威胁的前提下，使跳频周期、跳频间隔的联合不确定性最大。

将态势感知设备获取的实时环境威胁因子作为条件类X，跳频周期规划作为目标类Y，跳频间隔规划作为目标类Z，则可利用4.2节所确定的最大条件熵概率分布模型p∗(y,z|x )，对跳频周期和跳频间隔进行自适应规划，使其熵值为符合约束条件的最大值，则此时的跳频周期和跳频间隔参数既满足战场威胁环境，又具有低被截获能力。

5 仿真结果分析

5.1 初始化样本空间

为确定最大条件熵概率分布模型p∗(y,z|x )，应首先确定样本空间中x的概率密度函数(x)和x, y, z的联合概率密度函数(x,y,z)。本节设置Xp为先验威胁因子空间，Yp为先验跳频周期空间，Zp为先验跳频间隔空间。考虑到搭载平台的态势感知能力和计算能力均为受限系统，为方便计算，设置威胁因子σ在[0,8]内取整数值，且符合正态分布特征。从实际战场需求出发，跳频周期和跳频间隔约束规则应为：目标区域的威胁因子σ越大，则跳频周期越小，跳频间隔越大。本节仿真实验以JTIDS指标为基础，JTIDS跳频系统的跳频速率为0.013 ms，跳频间隔为30 MHz[19,20]，假定样本空间满足的约束特征如下表1所示。

则符合表1均值要求的样本空间分布特征如表2所示。

根据表1的约束特征，确定训练样本空间XpYpZp的特征函数fi(xp,yp,zp)为

5.2 求解拉格朗日乘子最优解

由4.2节可知，可利用HCPSO算法经过迭代运算求解拉格朗日最优解。HCPSO优化算法控制参数设置为：种群数为50，迭代次数为200，加速度常数c1, c2均为2，经迭代计算得到使目标函数式(10)最小的最优解，进而将最优解代入式(7)、式(8)，即可确定最大条件熵概率分布模型。

5.3 设定战场威胁因子环境

为验证基于最大条件熵的跳频周期、跳频间隔射频隐身联合设计方法的有效性，本节设定战场威胁因子环境Xenvt，来模拟真实情况下的战场威胁环境。Xenvt中的环境威胁因子在[0,8]内取值，满足正态分布特征，设置战场威胁因子空间Xenvt如表3所示。

5.4 仿真结果

为验证跳频周期、跳频间隔最大熵设计方法的有效性，本文将最大熵方法(Maximum Entropy Method, MEM)与固定周期、间隔方法进行了对比。单阈值策略为：设置阈值W1=4，当威胁因子σ≤4时，跳频周期Tg=0.06 ms ，跳频间隔Fg= 30 MHz，当威胁因子σ＞4时，跳频周期Tg= 0.02 ms，跳频间隔Fg=70 MHz 。双阈值策略为：设置阈值W1=2,W2=5，当威胁因子σ≤2时，跳频周期Tg=0.06 ms，跳频间隔Fg=30 MHz ，当威胁因子2＜σ≤5时，跳频周期Tg=0.04 ms，跳频间隔Fg=50 MHz，当威胁因子σ＞5时，跳频周期Tg=0.02 ms，跳频间隔Fg=70 MHz 。

仿真1 跳频周期、跳频间隔性能比较

跳频周期和跳频间隔是跳频系统的重要参数，直接影响敌方截获接收机分选、识别跳频信号的能力。本节针对最大熵方法、单阈值方法(SingleThreshold Method, STM)和双阈值方法(Double Threshold Method, DTM)分别进行了仿真计算，3种策略下的跳频周期曲线和跳频间隔曲线分别如图1和图2所示。由仿真图可知，采用STM和DTM策略的跳频周期、跳频间隔，分别在2个或3个固定取值间变化，而MEM策略的跳频周期、跳频间隔则在取值范围内随机变化，因此，MEM策略具有较强的抗截获、抗分选能力。

表1 样本空间约束特征

表2 样本空间分布特征

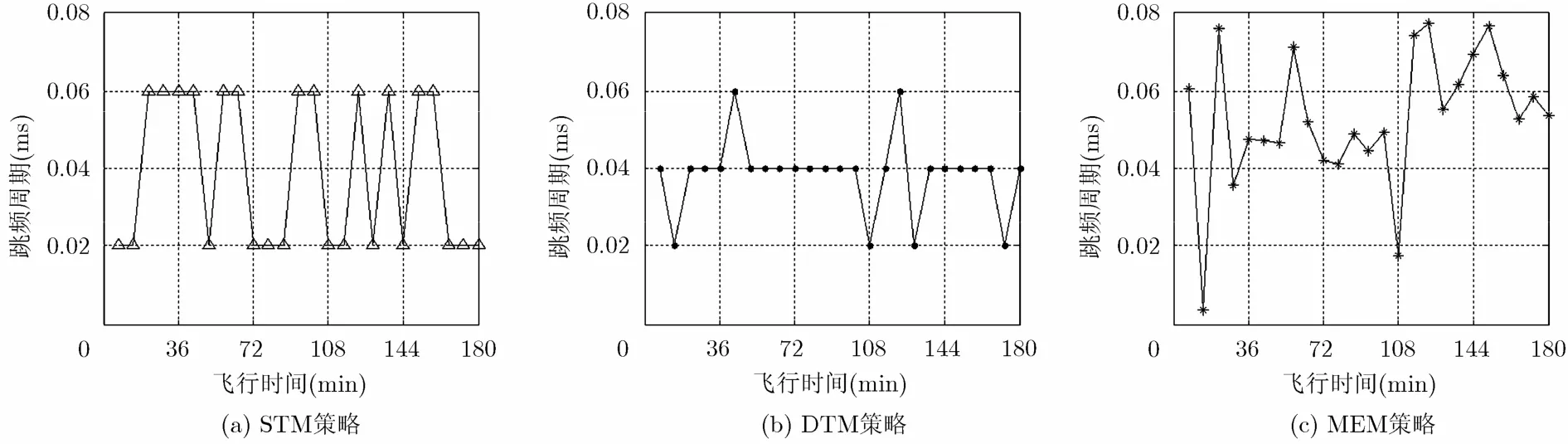
图1 3种策略下的跳频周期曲线

图2 3种策略下的跳频间隔曲线

表3 战场威胁因子空间Xenvt

仿真2 跳频周期、跳频间隔不确定性比较

由第2节可知，熵是不确定性的数学度量，因此，跳频系统的不确定性可以通过熵来衡量。为评价STM, DTM和MEM对跳频系统射频隐身性能的影响，本节依据5.3节设置的环境威胁因子环境对3种方法进行仿真计算，STM, DTM和MEM 3种方法的熵值分别如表4所示。

由表4可知，MEM的不确定性远优于STM和DTM，即MEM具有最优的射频隐身性能。

仿真3 跳频周期、跳频间隔环境适应性比较

最大信号不确定性要求跳频周期和跳频间隔的不确定性越大越好，但信号参量的不确定性越大，对系统设计的要求则越高，同时耗费的资源也越多。因此，最佳的不确定性设计应与环境威胁相适应。本节通过STM, DTM和MEM的跳频周期和跳频间隔均值来分析这3种方法的环境适应性。3种方法的跳频周期均值和跳频间隔均值分别如图3和图4所示。

表4 MEM, STM和DTM方法的熵值

3种方法均随着环境威胁因子的增加，逐渐减少跳频周期，增大跳频间隔，因此，均具有一定的环境适应性，其中DTM和MEM对于不同威胁因子具有较高的环境区分度。

仿真4 截获概率性能比较

跳频信号的射频隐身性能可以通过截获概率进行衡量，截获概率越低，射频隐身性能越好。本节针对MEM, STM和DTM分别进行了仿真计算，参数设置为：MF=11.2 m2, PI=−113 dBW , CO=0.477, DI=0.001, TI=5 s 3种策略下截获概率性能曲线分别如图5和图6所示。

由仿真结果可知，固定阈值方法中DTM的截获概率普遍低于STM, DTM的射频隐身性能优于STM。而最大熵方法的截获概率比固定阈值方法低4个数量级左右，其射频隐身性能要显著优于STM和DTM。该结论与仿真实验2所得3种方法的熵值相一致，因此MEM方法具有最优的射频隐身性能。

6 结束语

本文从提高跳频系统跳频周期和跳频间隔不确定性入手，提出了一种跳频系统射频隐身联合设计方法。该方法基于目标区域的环境威胁信息，利用最大条件熵模型对跳频周期和跳频间隔进行自适应规划。仿真结果表明，与STM和DTM方法相比，MEM具有最大的不确定性和最低的截获概率，且针对不同威胁因子具有较高的环境区分度，具有较好的射频隐身性能，可以有效提高搭载平台的生存能力。但相较传统的固定周期、间隔方法，MEM产生了较多的跳频周期和频率间隔参数，且要求较高的跳变速率，这些均对硬件系统提出了更高要求。目前跳频系统多采用FPGA平台搭建，频率信号则利用直接数字信号合成器(Direct Digital Synthesizer, DDS)产成，DDS通过相位累加器和频率控制字可以生成任意频率信号，且频率转换时间仅为纳秒数量级，随着未来器件性能的进一步提高，硬件系统可以满足MEM带来的硬件开销。

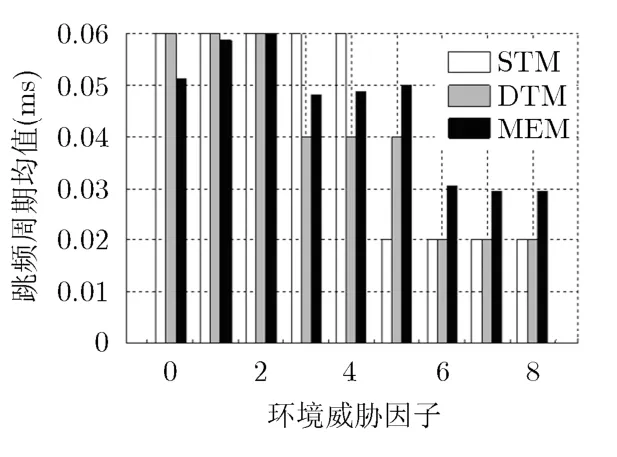
图3 不同威胁因子下的跳频周期均值

图4 不同威胁因子下的跳频间隔均值

图5 固定阈值法截获概率

图6 最大熵方法截获概率

[1] Schleher D C. LPI radar: fact or fiction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 21(5): 3-6.

[2] Gao J Y. Analysis of low probability of intercept (LPI) radar signals using the wigner distribution[D]. [Ph.D. dissertation], Naval Post Graduate School, 2002.

[3] 杨红兵, 周建江, 汪飞, 等. 飞机射频隐身表征参量及其影响因素分析[J]. 航空学报, 2010, 31(10): 2040-2045. Yang Hong-bing, Zhou Jian-jinag, Wang Fei, et al.. Characterization parameters of warplane RF stealth and analysis of its affecting factors[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(10): 2040-2045.

[4] Lempel A and Greenberger H. Families sequence with optimal Hamming correlation properties[J]. IEEE Transactions on Information Theory, 1974, 20(1): 90-94.

[5] Han H Y and Peng D Y. Set of optimal frequency-hopping sequences based on polynomial theory[J]. Electronics Letters, 2014, 50(3): 214-216.

[6] Liu X and Peng D Y. Theoretical bound on frequency hopping sequence set[J]. Electronics Letters, 2013, 49(10): 654-656.

[7] 杨宇晓, 周建江, 陈军, 等. 基于最大条件熵的射频隐身数据链猝发通信模型[J]. 航空学报, 2014, 35(5): 1385-1393.

Yang Yu-xiao, Zhou Jian-jiang, Chen Jun, et al.. Burst communication datalink model for radio frequency stealth based on conditional maximum entropy[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1385-1393.

[8] Mukumoto K, Nagata S, Wada T, et al.. Proposal of go-back-i-symbol ARQ scheme and its performance evaluation in meteor burst communications[J]. IEEE Transactions on Communications, 2012, 60(8): 2336-2343.

[9] Snow T and Chappell W J. Applications for directional modulation on a digital phased array[C]. Proceedings of the IEEE International Symposium on Phased Array Systems & Technology, Waltham, USA, 2013: 529-533.

[10] Chappell W J and Snow T. Directional modulation using independent waveforms at each element of a phased array radar[C]. Proceedings of the IEEE International Symposium on Microwave Digest (IMS), Seattle, USA, 2013: 1-4.

[11] Arun K K. A secure frequency hopping synthesizer for reconfigurable wireless radios[C]. Proceedings of the IEEE Conference on Information & Communicaion Technologies (ICT), Jeju, Korea, 2013: 851-854.

[12] Shao L J and Sun J J. The performance of analysis of anti-reconnaissance based on carrier aggrega-tion & frequency hopping communication system[C]. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing(WiCOM), Wuhan, China, 2011: 1-3.

[13] Liang T, Zhang J M, and Chen Y. Modeling and simulation of frequency hopping anti-jamming communication system[C]. Proceedings of the International Conference on Modeling, Simulation and Visualization Methods(WMSVM), Sanya, China, 2010: 250-253.

[14] Jaynes E T. Information theory and statistical mechanics[J]. The Physical Review, 1957, 106(4): 620-630.

[15] David L J. Introduction to RF Stealth[M]. Raleigh, North Carolina: Science Technology Publishing Incorporation, 2004: 8-12.

[16] 胥小波, 郑康锋, 李丹, 等. 新的混沌粒子群优化算法[J]. 通信学报, 2012, 33(1): 24-30.

Xu Xiao-bo, Zheng Kang-feng, Li Dan, et al.. New chaosparticle swarm optimization algorithm[J]. Journal of Communication, 2012, 33(1): 24-30.

[17] Shan Q and Wang J C. Solve capacitated vehicle routing problem using hybrid chaotic particle swarm optimization[C]. Proceedings of the International Symposium on Computational Intelligence and Design(ISCID), Hangzhou, China, 2013: 422-427.

[18] Lin W C, Hsu S C, and Cheng A C. Mass detection in digital mammograms system based on PSO algorithm[C]. Proceedings of the International Symposium on Computer, Consumer and Control(IS3C), Taichung, China, 2014: 662-668.

[19] 申振宁, 曾兴雯, 周子琛, 等. JTIDS系统仿真与性能分析[J].计算机仿真, 2005, 22(2): 23-25. Shen Zhen-ning, Zeng Xing-wen, Zhou Zi-chen, et al.. Simulation and performance analysis of JTIDS[J]. Computer Simulation, 2005, 22(2): 23-25.

[20] Liu H B, Jun G, Tang S, et al.. Analysis of the coding performance and performance of anti-jamming of JTIDS[C]. Proceedings of the International Conference on Consumer Electronics, Communications and Networks(CECNet), Xianning, China, 2013: 149-154.

杨宇晓： 男，1984年生，博士生，助理研究员，研究方向为射频隐身技术、卫星通信等.

汪 飞： 男，1976年生，博士，副教授，研究方向为射频隐身技术、雷达目标识别、阵列信号处理等.

周建江： 男，1962年生，博士，教授，博士生导师，研究方向为射频隐身技术、雷达目标识别、阵列信号处理等.

RF Stealth Design Method for Hopping Cycle and Hopping Interval Based on Conditional Maximum Entropy

Yang Yu-xiao①②Wang Fei②Zhou Jian-jiang②Kang Guo-hua①

①(College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

②(Key Laboratory of Radar Imaging and Microwave Photonics, Nanjing 210016, China)

In order to increase the interception performance of frequency hopping systems, an optimal algorithm for hopping cycle and hopping interval, which is based on the conditional maximum entropy is proposed. The prior data of frequency hopping systems are used as the training sample space, and the Lagrange multipliers are selected as optimized variables. The Hybrid Chaotic Particle Swarm Optimization (HCPSO) algorithm is used for the optimization of the dual programming of the conditional maximum entropy. Compared with the Single Threshold Method (STM) and the Double Threshold Method (DTM), the simulation results show that the proposed Maximum Entropy Method (MEM) not only has the greatest uncertainty of hopping cycle and hopping interval, it also has the lowest probability of intercept and higher environmental differentiation with threat factors. So the MEM has good RF stealth performance and it can effectively improve the survival ability of the platform.

Frequency hopping communication; Radio frequency stealth; Hopping cycle; Hopping interval; Hybrid Chaotic Particle Swarm Optimization (HCPSO) algorithm

TN914.4

： A

：1009-5896(2015)04-0841-07

10.11999/JEIT140892

2014-07-07收到，2014-12-23改回

航空科学基金(20130152002)，上海航天科技创新基金(SAST 201411)，中央高校基本科研业务费专项资金和江苏省普通高校研究生科研创新计划(CXZZ11_0212, NP2015505)资助课题

*通信作者：周建江 zjjee@nuaa.edu.cn