基于Berlekamp-Justesen码的压缩感知确定性测量矩阵的构造

夏树涛刘 璐 刘鑫吉

(清华大学深圳研究生院 深圳 518055)

(清华大学计算机科学与技术系 北京 100084)

基于Berlekamp-Justesen码的压缩感知确定性测量矩阵的构造

夏树涛*刘 璐 刘鑫吉

(清华大学深圳研究生院 深圳 518055)

(清华大学计算机科学与技术系 北京 100084)

确定性测量矩阵构造是近期压缩感知领域的一个重要研究问题。该文基于Berlekamp-Justesen(B-J)码，构造了两类确定性测量矩阵。首先，给出一类相关性渐近最优的稀疏测量矩阵，从而保证其具有较好的限定等距性(RIP)。接着，构造一类确定性复测量矩阵，这类矩阵可以通过删除部分行列使其大小灵活变化。第1类矩阵具有很高的稀疏性，第2类则是基于循环矩阵，因此它们的存储开销较小，编码和重构复杂度也相对较低。仿真结果表明，这两类矩阵常常有优于或相当于现有的随机和确定性测量矩阵的重建性能。

压缩感知；Berlekamp-Justesen码；渐近最优；复测量矩阵；限定等距性

1 引言

自2006年Candès等人[1]提出压缩感知(Compressive Sensing, CS)以来，这种提高海量数据压缩采样效率的新思路引起了海内外学者的广泛关注。压缩感知过程分为两部分：压缩采样和信号重构[2]。压缩采样过程主要关注的是如何构建有效且鲁棒的测量矩阵，这也是本文的重点研究内容。信号重构重点考虑从低维压缩采样数据中恢复出原始的高维信号，可靠重建的相关算法可见文献[1,3]。

限定等距性(Restricted Isometry Property, RIP)[1,4]是保证压缩感知信号重建鲁棒性的一个很重要的概念。如果一个测量矩阵满足限定等距性，那么这个矩阵就可以用来对信号进行采样，并在信号重构中保证原始信号的稳定和鲁棒恢复。

相关性(coherence)是建立矩阵RIP的一个重要方法。Bourgain等人[5]指出m×n的矩阵Φ的相关系数μΦ与限定等距常量δk存在关系：矩阵Φ满足k＜1/μΦ+1阶RIP，即δk≤μΦ(k−1)。然而，根据Welch界[6]，当n≫m时，μΦ的下界渐近为μΦ≥ 1/。因此，如果从矩阵的相关性角度来看，至多能构造出满足k=O()阶RIP的确定性测量矩阵，称这类矩阵为相关性意义下的渐近最优测量矩阵。

很多随机矩阵已经被证明是很好的压缩感知测量矩阵[7]。一些大小为m×n随机测量矩阵，很大概率上满足k=O(m/log2(n/m))阶RIP[8]，这些矩阵很容易就可以实现，也能很好地恢复稀疏信号。但是，它们的存储开销相对较高，且在硬件上较难实现。因此，构造存储量小且性能等价于或优于随机测量矩阵的确定性测量矩阵就显得意义重大。

目前国内外已经有不少学者提出了很多确定性测量矩阵构造方法。文献[9]提出了一种基于Chirp函数的2m×m复测量矩阵；文献[10]利用光正交码构建了一类三元测量矩阵；文献[11]基于Reed-Solomon码构建了一类相关性较小的测量矩阵。近期，浙江大学李抒行等人[12]基于有限几何构造了一大类稀疏的二元测量矩阵。文献[13]对现有的压缩感知确定性测量矩阵的构造给出了一个比较完善的综述。

基于Berlekamp-Justesen (B-J)码，文献[14]构造了一类性能优异的低密度奇偶校验(Low Density Parity Check, LDPC)码，并将这类LDPC码的校验矩阵直接作为测量矩阵应用到压缩感知中[15]，这类矩阵称为B-J矩阵。本文基于此B-J矩阵，提出了两类确定性测量矩阵的构造方法。一类通过在B-J矩阵中嵌入Hadamard矩阵或DFT矩阵，使测量矩阵保持稀疏性，并且相关性达到渐近最优。而另一类则构建了矩阵大小较为灵活的确定性复测量矩阵[16]，这类矩阵基于循环矩阵，因此存储开销也较小。本文中针对提出的两类测量矩阵进行仿真实验，实验结果表明这两类矩阵常常比一些随机矩阵和确定性测量矩阵效果更好。

2 二元B-J矩阵的构造

本节简单介绍有限域内q -元B-J码的构造和二元B-J测量矩阵的构造。更多的细节可以见文献[14]。

2.1 q -元B-J码

令q=2，其中是一个整数，令CBJ为q-元B-J码。通过对多项式xq+1−1的分解，CBJ的生成多项式可以写为

CBJ中的所有码字为

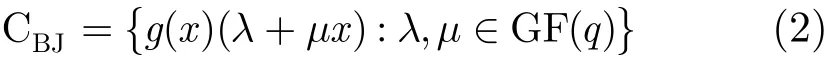
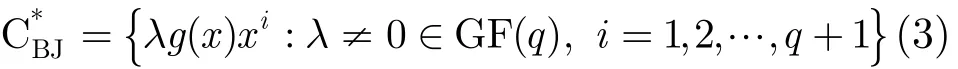
2.2 第1类B-J矩阵：通过q -元组替换B-J码

已知GF(q)={0,1,α,α2,…,αq−2}，且αq−1=1，记α−∞=0。定义αj(j=−∞,0,1,…,q−2)在GF(q)中的位置向量为y(αj)=(y−∞,y0,y1,…,yq−2)，其中yj=1，其他元素均为0。

对于i =−∞,0,1,…,q−2，定义CBJ中的码字子集为

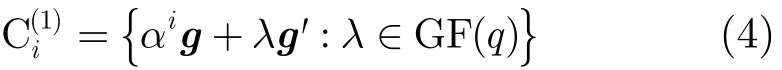
其中g =(1,g1,g2,…,gq−1,0),g '=(0,1,g1,g2,…,gq−1)。

设Ai(1)为GF(q)上C(i1)中的所有码字作为行组成的矩阵。对i=−∞,1,2,…,q+1，用q -元组替换Ai(1)中每个元素，则得到q×(q+1)q 的矩阵Bi(1)= (JiPi(,11)…Pi(,q1))。最后的矩阵H(1)=(B−(1∞)B0(1)B(1)…B(1−))T。

1q2

2.3 第2类B-J矩阵：通过(q -1)-元组替换B-J码

定义αj(j=0,1,…,q−2)在GF(q)中的位置向量为y(αj)=(y0,y1,…,yq−2)，其中yj=1，其他元素均为0，GF(q)中的0位置向量则为全0的(q -1)-元组。

对i=1,2,…,q +1，定义C*BJ中的一个码字子集为

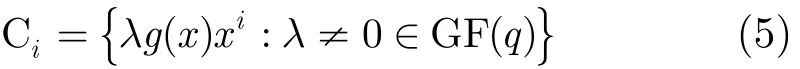
3 相关性渐近最优的稀疏矩阵构造

本节基于B-J矩阵提出一类相关性渐近最优的稀疏矩阵构造方法。通过采用Hadamard矩阵或者DFT(Discrete Fourier Transform)矩阵对B-J矩阵进行扩展，对于固定的m值，增加矩阵的列生成稀疏测量矩阵。这种列的增加就生成了适用于压缩感知测量矩阵的相关性渐近最优的稀疏矩阵。

定义1 (相关性) 设φi, φj是测量矩阵Φm×n的任意两列，则矩阵的相关性为

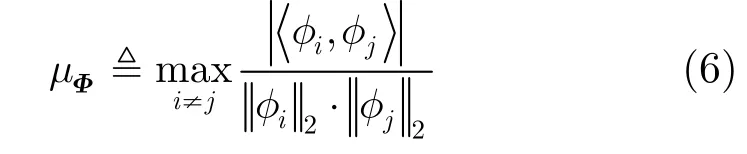
3.1 构造方法

将B-J矩阵与其他相关性很小的矩阵(例如Hadamard矩阵和DFT矩阵)嵌套生成新的矩阵，利用特殊方式嵌套生成的矩阵可以使相关性达到渐近最优。这种特殊的嵌套方式在文献[17]中最先提出。

首先，构造列重相同的二元矩阵A，本文中即为B-J矩阵，令q=2，则生成的两类B-J矩阵列重均为q。其次，构造相关性很小的q×q矩阵B。最后，将矩阵A的每一列中第i个1替换成矩阵B的第i行(i=1,2,…,q )，从而生成相关性渐近最优的稀疏矩阵C。记这种嵌套模式为A⊙B ，如图1所示。

图1 矩阵结合模式：A是有常数列重的二元矩阵，B的行数与此常数列重相同

引理1[17]给定一个列重为wm的二元矩阵Am×n1，相关性为μA。矩阵B的大小为wm×n2，相关性为μB。令Cm×(n1n2)=Am×n1⊙Bwm×n2，则其相关性μC=max(μA,μB)。

3.2 嵌套Hadamard矩阵生成相关性渐近最优的测量矩阵

Hadamard矩阵[18]是由元素1和-1生成的方阵，矩阵的任意两列都是正交的。2阶的Hadamard矩阵为：。

如果H2k−1是一个2k−1阶的Hadamard矩阵，则：，其中，

证明 H(1)的任意两列的1中最多有一个位置相同，任意两行的1中也最多有一个位置相同。所以，矩阵的任意两列内积的最大值为1，即：，其中hi与hj为矩阵H(1)的任意两列。

另外，因为H(1)的列重为q，显然，H(1)的相关性为：μH(1)=1/q 。

因为Hadamard矩阵的相关性为0。根据引理1，Φ(1)的相关性μ=1/q，达到了渐近最优。 证毕

证明 矩阵H(2)的任意两列内积的最大值为1，且H(2)的列重为q，则H(2)的相关性为：μH(2)=1/q。根据引理1, Φ(2)的相关性μ=1/q，达到了渐近最优。 证毕

3.3 嵌套DFT矩阵生成相关性渐近最优的测量矩阵随机傅里叶(DFT)矩阵定义[19]：

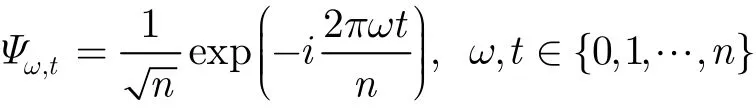
记Ψq为阶为q的DFT矩阵，则Ψq为

定理3 设q=2，令Φ(3)=H(1)⊙Ψq，则Φ(3)大小为q2×(q3+q2)，相关性μ=1/q，达到了渐近最优。

证明 矩阵H(1)的相关性为：μH(1)=1/q ，DFT矩阵的相关性为0。则Φ(3)的相关性μ=1/q。

证毕

定理4 设q=2，令Φ(4)=H(2)⊙Ψq，则Φ(4)大小为(q2−1)×(q3−q)，相关性μ=1/q，达到了渐近最优。

证明 矩阵H(2)的相关性为：μH(2)=1/q ，DFT矩阵相关性为0。则Φ(4)的相关性μ=1/q。

证毕

表1总结了上述相关性意义下渐近最优的测量矩阵，其中μ是矩阵相关性，k是稀疏性，q是素数幂。

3.4 矩阵大小调整

对于一些确定性测量矩阵，删除部分行列后得到的子矩阵恢复效果相对较差，但是本节提出的渐近最优矩阵在删除部分行列后性能仍常常较好，仿真效果详见5.1节。下面简单介绍一下矩阵行列的删除方法。

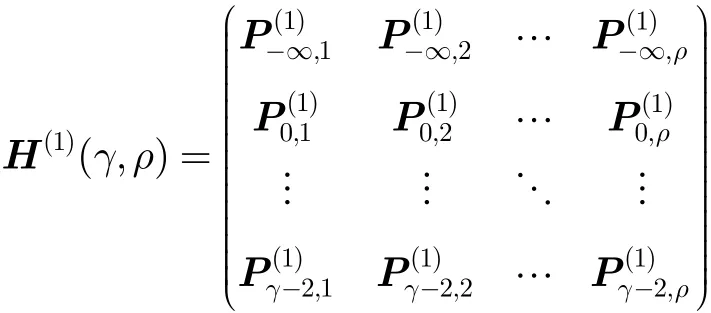
表 1 大小为m×n的感知矩阵总结

针对第2类二元B-J矩阵，对任意2≤γ≤ρ≤q , 0≤u≤q−1，当ρ=q+1时，u=0，则调整大小后的矩阵H(2)(γ,ρ,u)为

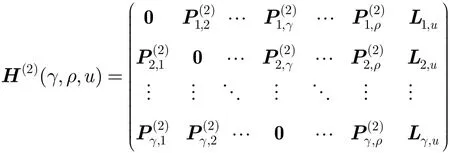
其中Li,u(i=1,2,…,γ)是从中删除最后q−1−u列得到的。的最后(ρ−γ)(q−1)+u列。则最终得到的子矩阵大小为γ(q−1)×[ρ(q−1)+u]l。

选取Hadamard矩阵或者DFT矩阵的前l列得到子矩阵，从子矩阵中选取前γ−1行嵌入到第2类B-J矩阵的子矩阵(2)(γ,ρ,u) H的前γ(q−1)列，然后从子矩阵中选取前γ行嵌入到子矩阵(2)(γ,ρ,u) H中

4 复测量矩阵的构造

本节基于B-J矩阵，提出一类复测量矩阵的构造方法。此类矩阵为循环矩阵，因此，矩阵的存储量小，而且矩阵大小调整更为灵活。

其中gi≠0∈GF(q )，并且xq+1=1。设A(λ)是GF(q)上以C(λ)的所有码字作为行生成的(q+1)×(q+1)矩阵。已知GF(q)={0,α,α2,…,αq−2}，αq−1=1，然后将每个A(λ)中的元素αi替换成i(i∈[1,q−1])，将A(λ)中的0替换成0。A(λ)是循环矩阵，这样在实际应用中可以大大节省存储空间。

从矩阵A(λ)中选取前m行和前n列，得到子矩阵A(m,n,λ)，m和n根据本文的需求来定。最后，将矩阵A(m,n,λ)中每一个整数k∈[0,q−1]通过式(8)转化成复平面单位圆上的点，并将结果矩阵标准化，这样就生成了复测量矩阵(2)(m,n,λ) A：

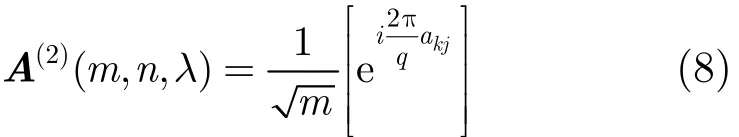
其中i为复数虚数单位，akj为矩阵A(m,n,λ)的第k行第j列元素。

因为g(x)所生成的码字为一个伪随机序列，则A(λ)矩阵的每一行均相当于一个伪随机序列，所以，得到的矩阵性能较好。构建算法见表2。

表 2 复测量矩阵构建算法步骤

这类矩阵的构造算法复杂度稍高，但是确定性测量矩阵只需要生成一次，而因为其循环特性大大减小了存储量，同时对稀疏信号的恢复效果也比较好，详见5.2节仿真部分。

5 仿真实验

本节对提出的相关性渐近最优稀疏矩阵和复值矩阵作为测量矩阵进行实验，将信号恢复效果与一些随机矩阵和确定性测量矩阵相比较。其中随机矩阵包括：随机高斯矩阵和随机DFT矩阵(随机选择DFT矩阵的行)，确定性测量矩阵包括：BCH矩阵[17]和基于Chirp函数构造的矩阵[9]。

5.1 相关性渐近最优稀疏矩阵

5.1.1 嵌套Hadamard矩阵生成的相关性渐近最优稀疏矩阵 令q=24，第1类B-J矩阵H(1)的大小为256×272，通过嵌套16阶的Hadamard矩阵得到的相关性渐近最优的稀疏矩阵Φ(1)大小为256×4352，矩阵的相关性为1/16。令γ=12,ρ=16,l=12，得到的子矩阵大小为192×3072。为了更好地进行评估，本文实现相同大小的随机矩阵作为测量矩阵进行信号恢复：随机高斯矩阵(在图中标为“Rnd”)。利用这些测量矩阵进行信号恢复所得到的信号完全恢复百分比结果见图2(相关性渐近最优稀疏矩阵标注为“BJ1+Had”)。可见，此矩阵信号恢复效果比随机矩阵效果好。

令q=24，第2类B-J矩阵H(2)的大小为255×255，通过嵌套16阶的Hadamard矩阵得到的相关性渐近最优稀疏矩阵Φ(2)大小为255×4080，矩阵的相关性为1/16。令γ=12, ρ=16, u=0, l=12，得到的子矩阵大小为180×3060。信号恢复所得到的信号完全恢复百分比结果见图3(相关性渐近最优稀疏矩阵标注为“BJ2+Had”)。容易看出，此矩阵信号恢复效果比随机矩阵效果好。

5.1.2 嵌套DFT矩阵生成的相关性渐近最优稀疏矩阵 令q=24，第1类B-J矩阵H(1)的大小为256×272，通过嵌套16阶的DFT矩阵得到的相关性渐近最优稀疏矩阵Φ(3)大小为256×4352，矩阵的相关性为1/16。令γ=12, ρ=16, l=12，得到的子矩阵大小为192×3072。为了更好地进行评估，本文使用相同大小的复值随机矩阵作为测量矩阵进行信号恢复：复值随机高斯矩阵(在图中标为“ComRnd”)和随机DFT矩阵(在图中标为“RndDFT”)。利用这些测量矩阵进行信号恢复所得到的信号完全恢复百分比结果见图4(相关性渐近最优稀疏矩阵标注为“BJ1+DFT”)。从图4可以看出，此矩阵信号恢复效果比随机矩阵效果好。

令q=24，第2类B-J矩阵H(2)的大小为255×255，通过嵌套16阶的DFT矩阵得到的相关性渐近最优稀疏矩阵Φ(4)大小为255×4080，矩阵的相关性为1/16。令γ=12, ρ=16, u=0, l=12，得到的子矩阵大小为180×3060。信号恢复所得到的信号完全恢复百分比结果见图5(相关性渐近最优稀疏矩阵标注为“BJ2+DFT”)。可见，此矩阵信号恢复效果比随机矩阵效果好。

5.2 复测量矩阵

对复测量矩阵进行仿真实验，将信号恢复效果与复值随机高斯矩阵、BCH矩阵[17]、基于Chirp函数的矩阵[9]和随机DFT矩阵(随机选择DFT矩阵的行)相比较。

令q=210, m=248, n=1023, λ=1，复测量矩阵A(2)(248,1023,1)的大小为248×1023。为了更好地进行评估，我们使用相同大小的复值矩阵作为测量矩阵进行信号恢复：BCH矩阵(在图中标为“BCH”)、基于Chirp函数的矩阵(在图中标为“Chirp”)、复值随机高斯矩阵(在图中标为“ComRnd”)和随机DFT矩阵(在图中标为“RndDFT”)。利用这些测量矩阵进行信号恢复所得到的信号完全恢复百分比结果见图6(最后的复测量矩阵标注为“q-ary Complex”)。图6显示出此矩阵信号恢复效果比随机矩阵效果好。

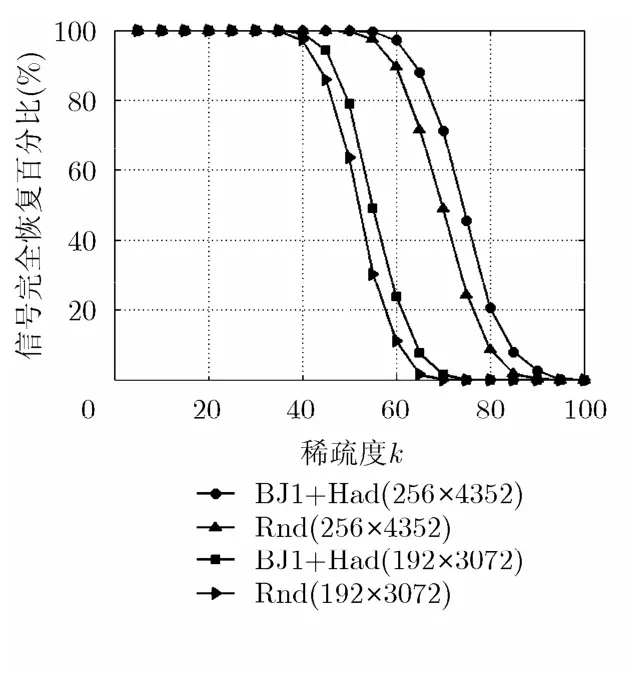
图2 256×4352相关性渐近最优矩阵Φ(1)和192×3072的子矩阵作为测量矩阵得到的信号完全恢复百分比随稀疏度变化

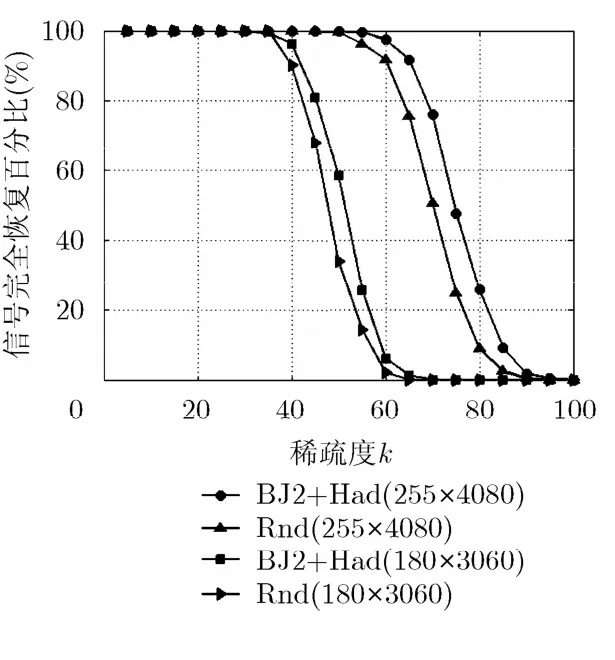
图3 255×4080相关性渐近最优矩阵Φ(2)和180×3060的子矩阵作为测量矩阵得到的信号完全恢复百分比随稀疏度变化

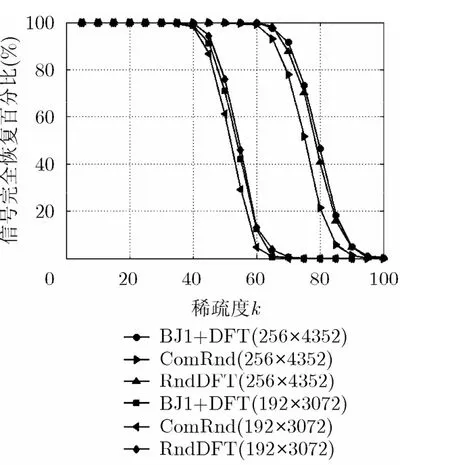
图4 256×4352相关性渐近最优矩阵Φ(3)和192×3072的子矩阵作为测量矩阵得到的信号完全恢复百分比随稀疏度变化

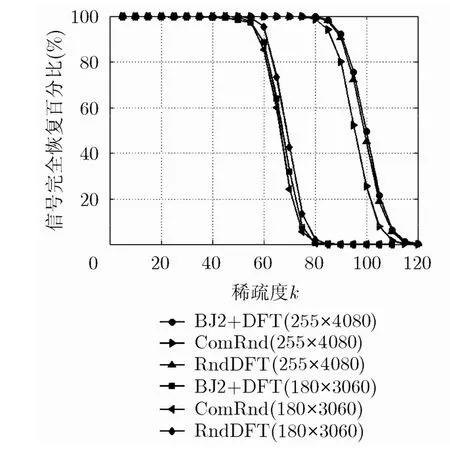
图5 255×4080相关性渐近最优矩阵Φ(4)和180×3060的子矩阵作为测量矩阵得到的信号完全恢复百分比随稀疏度变化

图6 248×1023的复测量矩阵A(2)(248,1023,1)作为测量矩阵得到的信号完全恢复百分比随稀疏度变化

最后，本文对512×512的辣椒图进行信号恢复，见图7。原始图像信号通过DCT块变换，图像压缩采样率为0.2(k/n=0.2)(自然图像的块恢复压缩感知算法见文献[20])。将图像分为16×16块，本文利用205×1024复测量矩阵A(2)(205,1024,1)对每一块图像压缩采样，并进行图像恢复。从图7可以看出，复测量矩阵恢复图像的PSNR值比其他矩阵要好。

与图7仿真实验相同，对512×512的辣椒图进行信号恢复，原始图像进行DCT变换。将图像分为16×16块，图像压缩采样率为γ，对每一块辣椒图分别通过大小为1024γ×1024的不同测量矩阵进行压缩采样，并进行信号恢复，结果见图8。从图8可以看出，在压缩采样率比较小的情况下(小于0.5)，复测量矩阵恢复图像的PSNR值比其他矩阵要好。

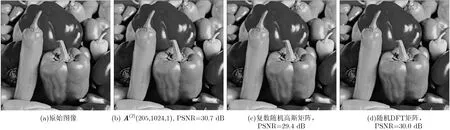
图7 利用不同测量矩阵对图像压缩采样所得到的图像恢复效果

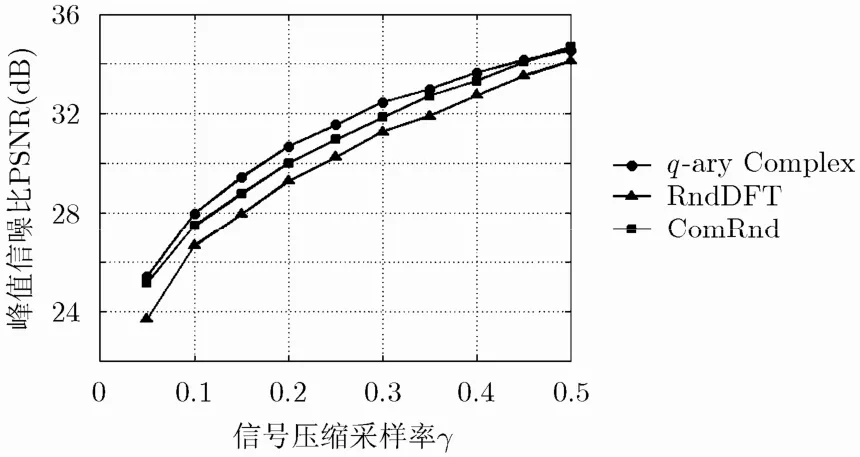
图8 复测量矩阵图像恢复得到的PSNR随压缩采样率变化

6 结束语

本文基于Berlekamp-Justesen(B-J)码，构造了两种确定性测量矩阵：一种是相关性渐近最优的确定性稀疏测量矩阵，另一种是确定性复测量矩阵。本文对相关性渐近最优的确定性稀疏测量矩阵给出了灵活调整矩阵大小的方法；而确定性复测量矩阵可以通过简单删除部分行和列使其大小灵活变动。另外，这两类矩阵中第1类有很高的稀疏性，第2类基于循环矩阵，所以具有存储开销较小、编码和重构复杂度相对较低等优良特性。仿真结果表明，在许多情况下，本文提出的两种矩阵比一些随机矩阵和确定性测量矩阵效果更好。

[1] Candès E J, Romberg J, and Tao T. Robust uncertainty principles: Exact signal reconstruction from highlyincomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2] 金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2): 470-475. Jin Jian, Gu Yuan-tao, and Mei Shun-liang. An introduction to copressive sampling and its applications[J]. Journal of Electronics & Information Technology, 2010, 32(2): 470-475.

[3] Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

[4] Candès E J and Tao T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.

[5] Bourgain J, Dilworth S, Ford K, et al.. Explicit constructions of RIP matrices and related problems[J]. Duke Mathematical Journal, 2011, 159(1): 145-185.

[6] Welch L. Lower bounds on the maximum cross correlation of signals[J]. IEEE Transactions on Information Theory, 1974, 20(3): 397-399.

[7] Baraniuk R, Davenport M, DeVore R, et al.. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation, 2008, 28(3): 253-263.

[8] Candès E J and Tao T. Near-optimal signal recovery from random projections: universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[9] Applebaum L, Howard S D, Searle S, et al.. Chirp sensing codes: deterministic compressed sensing measurements for fast recovery[J]. Applied and Computational Harmonic Analysis, 2009, 26(2): 283-290.

[10] Yu Nam Yul and Zhao Na. Deterministic construction of real-valued ternary sensing matrices using optical orthogonal codes[J]. IEEE Signal Processing Letters, 2013, 20(11): 1106-1109.

[11] Mohades M, Mohades A, and Tadaion A. A Reed-Solomon code based measurement matrix with small coherence[J]. IEEE Signal Processing Letters, 2014, 21(7): 839-843.

[12] Li Shu-xing and Ge Gen-nian. Deterministic construction of sparse sensing matrices via finite geometry[J]. IEEE Transactions on Signal Processing, 2014, 62(11): 839-843.

[13] 王强, 李佳, 沈毅. 压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报, 2013, 41(10): 2041-2050. Wang Qiang, Li Jia, and Shen Yi. A survey on deterministic measurement matrix construction algorithms incompressive sensing[J]. Acta Electronica Sinica, 2013, 41(10): 2041-2050.

[14] Ge Xin and Xia Shu-tao. LDPC codes based on Berlekamp-Justesen codes with large stopping distances[C]. Preceedings of IEEE Information Theory Workshop (ITW), Chengdu, 2006: 214-218.

[15] Li Dan-dan, Liu Xin-ji, and Xia Shu-tao. A class of deterministic construction of binary compressed sensing matrices[J]. Journal of Electronics (China), 2012, 29(6): 493-500.

[16] Liu Lu, Liu Xin-ji, and Xia Shu-tao. Deterministic complex-valued measurement matrices based on Berlekamp-Justesen codes[C]. Proceedings of IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi'an, China, 2014: 723-727.

[17] Amini A, Montazerhodjat V, and Marvasti F. Matrices with small coherence using p-ary block codes[J]. IEEE Transactions on Signal Processing, 2012, 60(1): 172-181.

[18] Pratt W, Kane J, and Andrews H C. Hadamard transform image coding[J]. Proceedings of the IEEE, 1969, 57(1): 58-68.

[19] Kalogerias D S and Petropulu A P. RIP bounds for naively subsampled Scrambled Fourier sensing matrices[C]. Proceedings of 48th Annual Conference on Information Sciences and Systems (CISS), Princeton, USA, 2014: 1-6.

[20] Gan Lu. Block compressed sensing of natural images[C]. Proceedings of 15th International Conference on Digital Signal Processing (DSP), Cardiff , UK, 2007: 403-406.

夏树涛： 男，1972年生，教授，博士生导师，研究方向为信道编码、网络编码和压缩感知等.

刘 璐： 女，1989年生，硕士生，研究方向为压缩感知确定性测量矩阵构造.

刘鑫吉： 男，1989年生，博士生，研究方向为压缩感知、编码理论和分布式存储.

Deterministic Constructions of Compressive Sensing Matrices Based on Berlekamp-Justesen Codes

Xia Shu-tao Liu Lu Liu Xin-ji
(Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, China)
(Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China)

Nowadays the deterministic construction of sensing matrices is a hot topic in compressed sensing. Two classes of deterministic sensing matrices based on the Berlekamp-Justesen (B-J) codes are proposed. Firstly, a class of sparse sensing matrices with near-optimal coherence is constructed. It satisfies the Restricted Isometry Property (RIP) well. Afterwards, a class of deterministic complex-valued matrices is proposed. The row and column numbers of these matrices are tunable through the row and column puncturing. Moreover, the first proposed matrices are high sparsity and the second matrices are able to obtain from the cyclic matrices, thus the storage costs of them are relatively low and both the sampling and recovery processes can be simpler. The simulation results demonstrate that the proposed matrices often perform comparably to, or even better than some random matrices and deterministic measurement matrices.

Compressive Sensing (CS); Berlekamp-Justesen (B-J) codes; Near-optimal; Complex matrix; Restricted Isometry Property (RIP)

TN911.72

： A

：1009-5896(2015)04-0763-07

10.11999/JEIT140875

2014-07-02收到，2014-12-02改回

国家973计划项目(2012CB315803)，国家自然科学基金(61371078)和高等学校博士学科点专项科研基金(20130002110051)资助课题

*通信作者：夏树涛 xiast@sz.tsinghua.edu.cn