直径为3的极大加权双星图*
2015-07-12杜智华
王 娜,杜智华
(1.新疆师范高等专科学校,新疆 乌鲁木齐 830043;2.新疆师范大学,新疆 乌鲁木齐 830054)
直径为3的极大加权双星图*
王 娜1,杜智华2
(1.新疆师范高等专科学校,新疆 乌鲁木齐 830043;2.新疆师范大学,新疆 乌鲁木齐 830054)

加权图;双星图;Perron向量
1 预备知识
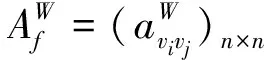
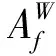
设F是边集E到多重集W的所有双射,给定G与W,ρ=max{ρ(Gf)|Gf∈G(G,W)},若存在映射f*∈F,并且满足ρ=ρ(Gf*),称Gf*(∈g(G,W))是极大加权图.
2 主要结论
设Gf∈g(G,W),S(a,b)是有n=a+b+2个顶点的双星图,u,v是两个中心且|N(u)v|=a,|N(v)u|=b,在这部分主要研究极大加权双星图(如图1).
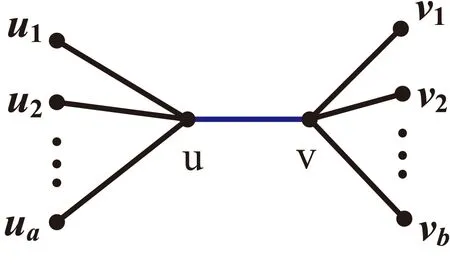
图1 极大加权双星图
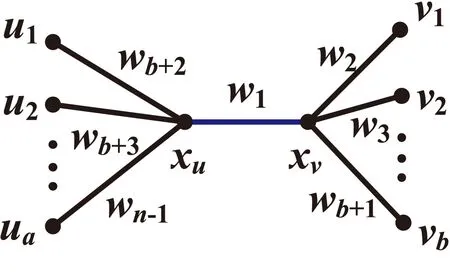
图2 赋权图
设Gf*∈g(S(a,b),W)是极大加权图,边u1u2的权值为Wu1u2,即f*(u1u2)=wu1u2xT=(x1,x2,…,xn)是Perron向量.
现在标记边集E={e1,e2,…,em},使得W=(wei|i=1,2,…,m)成递增减列即,
wei≥we2≥…≥wem
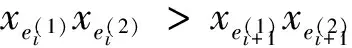
引理1 设B是一个非负实对称矩阵,λ1≥λ2≥…≥λn是B的n个特征值.如果有
λ=max‖x‖=1xTBx
则λ=λ1(ρ(B)).
引理2 设u,v是加权图G的两个顶点,v1,v2,…,vs∈NG(v)NG(u),xT=(x1,x2,…,xn)为GPerron向量,且xi与vi对应.G*是由删去G的边vvi再添加边uvi得到的,相应的令G*中的wuvi等于G中的wuvi(i=1,2,…,s).如果xu>xv,则ρ(G)<ρ(G*).
引理3 设Gf*∈g(G,W)是极大加权图,顶点u是star-center.Sr为u-star,它的叶子分别为u1,u2,…,ur,v(不是u叶子)是与相邻的点.设xT=(xp|p∈V(G))是Gf*的Perron向量,则有xu>xui以及xv≥xui(1≤i≤r).
引理4 设gf∈g(G,W),加权——邻接矩阵Af=(wvivj),则f与Perron向量xT=(x1,x2,…,xn)一致.
引理5 设Gf*∈g(G,W)是极大加权图,顶点u是star-center.Sr为u-star,它的叶子分别为u1,u2,…,ur,v(不是u叶子)是与相邻的点.设xT=(xp|p∈V(G))是Gf的Perron向量,则有xu>xui以及xv≥xui(1≤i≤r).
引理6 如果1≤a
证明 假设结论不成立,即xv≤xu.设p1,p2,…,pb是v的叶子,那么将边vqi(i=1,2,…,b-a)删去,再添加边uqi(i=1,2,…,b-a)并给其赋权值wvqi.这样我们得到一个新图Gf*.很明显Gf*∈g(S(s,b),W),但是由引理2可知ρ(Gf)>ρ(Gf*),从而矛盾.故有xv>xu.
证明 首先,由引理3可知xuxv≥xuxqi,xuxv≥xvxpj,所以由引理4可得wuv=w1.假设w2=w3=…=wn-1,由a=b,Gf*有两个自变群的轨道,其中xu,xv在一个轨道,其他的顶点在另外的一个轨道.由Perron向量的唯一性得到xu=xv(xpj=xqi,1≤i,j≤a).下面证明充分性.假设存在某个i,j(2≤i,j≤a,i≠j,)使得wi≠wj.设ρ=ρ(Gf*),从而可得,
(1)
分别从wuqi(1≤i≤a).wvpj(1≤j≤b)选取一个最大与最小者,不妨设为wuq1与wvp1,由(1)式可是wuq1 ρ(Gf)≥x'TA(Gf)x'=xTA(Gf*)x=ρ(Gf*) 由于Gf*是极大加权图,Gf∈g(S(a,b),W)以及ρ(Gf)=x'TA(Gf)x'=ρ(Gf*),那么由引理1可知x'为Gf的Perron向量.而x'u=x'v=xu=xv,从而有 这与(1)式矛盾,故w2=w3=…=wn-1. 定理8 设S(a,b)是有n=a+b+2个顶点的双星图,u,v是两个中心.任意给定一个权值集合W={w1,w2,…,wn-1|w1≥w2≥2≥…≥wn-1},SW(a,b)(图2),则SW(a,b)是g(S(a,b),W)中极大加权图. 证明 设Gf*=SW(a,b)∈g(S(a,b),W)是极大加权图,其Perron向量xT=(xp|p∈V(G)). 首先设a=b.若w1≥w2=…=wn-1,则由引理7可得xu=xv.进一步有xpj=xqi(1≤i,j≤a).那么由引理5得到,xuxv>xvxpj=xuxqi(1≤i,j≤a).从而根据引理4可知Gf*=SW(a,b)是极大加权图.其次,若存在1≤i,j≤a(i≠j)使得wi≠wj,可知xu≠xv.不失一般性,设xu xuxv>xvxpj≥min{xvxpj|j=1,2,…,b}≥ max{xuxqi|i=1,2,…,a} (2) 再由引理4可知,wuv>wvpj≥min{wvpj|j=1,2,…,b}≥max{wuqi|i=1,2,…,a},因此Gf*=SW(a,b)是极大加权图.最后假设a 在上面的讨论中,我们首先确立了直径为3的双星图的特征向量的分量之间的关系,进一步研究了当两个星的点数相等时,双星图的特征向量与加权映射的特性,从而找到了极大加权双星图.我们可以根据这一思路进一步考虑直径为4的树的极大加权图. [1]DCvetkoic,MDoob.SachsofGraphs-TheoyandApplications[J].thirdedJohannAmbrosiusbarthVerlag,1995, 20: 45-48. [2]DCvetkovic,PRowlinson,SSimic.Eigenspaceofgraphs[M].Combridge:CombridgeUniversitypress,1997. [3]YuanJinsongandShuJinlong.Ontheweightedtreeswhichhavethesecondlargestspectralradius[J].ORtransactions, 2006,10: 181-87. [4]王娜,杜智华.加权图的perron向量[J].兰州文理学院学报,2015(2):40-43. 10.13877/j.cnki.cn22-1284.2015.08.010 2015-04-10 国家自然科学基金项目“有向图的限制性连通度的研究”(11301452);新疆师范高等专科学校校级课题“新疆高等师范院校《数学分析》课程建设本土化研究”(XJJY201431);校级精品课程“数学分析” 王娜,女,新疆乌鲁木齐人,讲师. O A 1008-7974(2015)04-0024-033 结束语
