对地方病高危人群实施干预措施的时滞HIV/AIDS传播模型的持久性*

王来全，韩振岭，李 硕，魏成花

(1.昌吉职业技术学院，新疆 昌吉 831100；2.昌吉学院，新疆 昌吉 831100)

对地方病高危人群实施干预措施的时滞HIV/AIDS传播模型的持久性*

王来全1，韩振岭1，李 硕2，魏成花2

(1.昌吉职业技术学院，新疆 昌吉 831100；2.昌吉学院，新疆 昌吉 831100)

考虑了一类对高危人群实施干预措施的HIV/AIDS传播模型，给出了无病平衡点的全局稳定和地方病平衡点的局部稳定的条件，当R0>1时，讨论了疾病的持久性，同时，研究了对高危人群实施干预措施在HIV/AIDS预防中的效果.

干预措施；基本再生数；渐近稳定；持久

为了揭示传染病的传播规律，预测流行趋势,传染病数学模型迅速发展起来,许多学者对各种传染病模型平衡点的稳定性做了大量的研究工作，并得到很好的结果.文献[1-2]建立并研究了一类HIV/AIDS的传播模型,文献[3]研究了一类公众教育活动对预防HIV/AIDS的影响.基于文献[4-5]的理念,文献[6]研究了对一些易感者实施单一的教育活动对预防HIV/AIDS的传播的影响.但是,很少有人研究一类对高危人群实施干预措施的时滞HIV/AIDS传播模型的稳定性.在本文中，把易感人群分为高危易感人群和低危易感人群，在高危易感人群感染率大于低危易感人群的情况下,假设只对高危人群实施干预措施,讨论了地方病平衡点的局部渐近稳定性和疾病的持久性,同时，研究了对高危人群实施干预措施对预防HIV/AIDS传播的效果.

1 模型的建立

(1)

该数学模型的初值为：U(θ)=φ1，S(θ)=φ2，I(θ)=φ3，U(θ)=φ4，θ∈[-τ,0],其中φ=(φ1,φ2,φ3,φ4)T∈C,φi=φi(0)≥0(i=1,2,3,4).

C([-τ,0.R4])表示把连续函数从[-τ,0]映射到R4={(U,S,I,A)}的Banach空间.

2 平衡点和基本再生数

显然,系统(1)存在一个无病平衡点E0(U0，S0，0，0).其中,

计算出系统(1)的基本再生数R0.

当R0>1时，系统(1)存在一正地方病平衡点E1(U1,S1,I1,A1).

U1=

S1=

B2=

3 地方病平衡点的稳定性

为了分析地方病平衡点的稳定性,我们定义:x(t)=U(t)-U1,y(t)=S(t)-S1,z(t)=I(t)-I1,w(t)=A(t)-A1.则系统(1)在地方病平衡点E1(U1,S1,I1,A1)的线性方程为

(2)

定理1 如果R0>1,那么系统(1)的地方病平衡点E1(U1,S1,I1,A1)局部渐进稳定.

4 疾病的持久性

我们已经知道,对任意的t≥0,在初值条件下系统(1)的所有解为正解.设系统(1)的解(U,S,I,A)∈intΩ,将系统(1)的前两式相加得

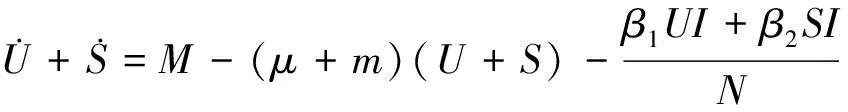
M-(μ+m+β1+β2)(U+S),

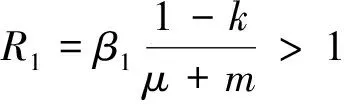
I(t)=

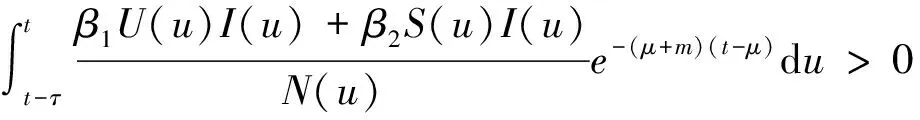
t>t1-τ

对所有的t>t1,因β2>β1,故有

I(t)>

t>t1-τ=

由以上式子推得

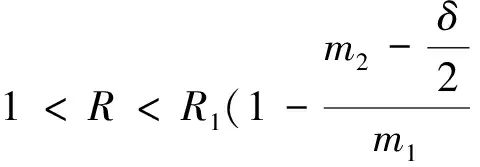
I(t1+τ)≥

如果断言不成立,则存在t3>t1+τ,对t1+τ≤t≤t3,使得I(t3)=m2R和I(t)≥m2R成立,

由定理2可以推出以下两个定理.

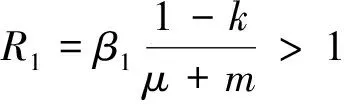
定理4 如果R0>1,则(1)的地方病持久.

5 干预措施对模型的影响效果

我们对模型(1)的基本再生数R0关于干预措施V0求导数即得

(3)

显然,基本再生数R0关于干预措施V0为单调递减的函数,从而为了降低基本再生数,可以加大干预措施的力度,达到降低HIV/AIDS疾病的传播.

6 结论

考虑了一类具有干预措施的HIV/AIDS传播模型,应用HIV/AIDS数学模型评估了高危人群实施干预措施对预防HIV/AIDS的传播影响,如果R0>1,证明了疾病将持久,特别地,我们从(3)式可以得到：对高危人群增强干预措施可以预防HIV/AIDS的蔓延,从而可以减少二次被感染的几率,如果本文的干预措施是教育和疫苗,则结果与文献[6]和[7]一致.

[1]MeleanAR,BlowerSM.Modellingvaccination[J].TrendsMicrobiol,1995,3:458-463.

[2]NyabadzaF.AmathematicalmodelforcombatingHIV/AIDSinsouthernAfriea:Willmultiplestrategieswork[J].BiolSyst,2006,14:357-372.

[3]BirkhoffG,RotaGC.Ordinarydifferentialequations[M].NewYork:JohnWiley,1982.

[4]MMusekwa-HoveSD,NyabadzaF.thedynamiesofanHIV/AIDSmodelwithscreeneddiseasecarriers[J].ComputMathMethodsMed,2009,10:287-305.

[5]ZhangTailei，Manhongjia,HongbingLuo,etal.StudyonaHIV/AIDSmodelwithapplieationtoYunmanprovince,China[J].AppliedMathematicalModelling, 2011,35:4379-4392.

[6]ZMukandavire,WGarira,JM.Tchuenche,modellingeffectsofpublichealtheducationalcampaignsonHIV/AIDStransmissiondynamicsg[J].Appliedmathmodelling,2009,33:2084-2095.

[7]PengmiaoHao,DejunFan,JunjieWei,etal.DynamicbehaviousofadelayedHIVmodelwithstage-strueture[J].CommumNonlinearSeiNumerSimulat,2012,17:4753-4766.

10.13877/j.cnki.cn22-1284.2015.08.008

2015-04-02

国家自然科学基金“人口流动对艾滋病传播影响的动力学模型研究”(11261056)；新疆自治区科技支撑项目“产城融合理念下新疆准东开发区产业优化与培育”(201442120)；昌吉职业技术学院自然科学基金“具有干预措施的HIV传播模型的建立与研究”(CJZY2015026)

王来全,甘肃定西人,教师．

王来全,E-mail:wanglaiquana@126.com；李硕,E-mail:lishuo6974@sina.com.

O

A

1008-7974(2015)04-0019-03