有效去除定位偏差的TDOA／FDOA闭合解定位算法

周 成，黄高明，高 俊

（海军工程大学 电子工程学院，湖北 武汉430033）

在目标辐射源所发射或者反射的信号中，含有从目标到接收站的时差（time difference of arrival，TDOA）和 频 差（frequency difference of arrival，FDOA）测量信息，结合接收站自身的位置和速度信息，可以得到关于目标位置和速度的非线性方程组［1-4］.无源定位方程具有高度的非线性，最直接的方法是采用搜索法［5-7］对目标的定位估计值进行求解，即对目标定位所有可能的取值进行遍历，并计算相应的目标函数，找到最优的目标定位估计值［8-10］.大量研究［11-13］发现，搜索法在较高噪声的条件下仍然能够保持较高的定位精度，但是存在计算量大，不满足实时性的缺点［14-15］.Lu等［16］提出了一种基于最大似然估计的泰勒算法（Taylor）.该方法将无源定位方程在估计值处进行泰勒级数（Taylor-Series）展开，从而将非线性的无源定位方程转化成线性形式.在噪声比较小的情况下，定位精度能够达到克拉美罗界（Cramér-Rao lower bound，CRLB）（CRLB是无偏估计器所能达到的最小估计误差均方值），但该方法面临初始点选择敏感和不一定收敛的问题.Ho等［17］提出了经典的基于两步加权最小二乘（two-step weighted least squares，两 步WLS）的TDOA／FDOA 定位算法.此算法将非线性TDOA／FDOA 定位方程转化成伪线性方程，再通过两步加权最小二乘运算，能够快速得到解析解，在适度的高斯TDOA／FDOA 噪声强度时，定位精度能达到CRLB，其在求解过程中不存在初始值选择和收敛的问题，运算量也比迭代算法要小.两步WLS算法是TDOA／FDOA 定位问题中经典的解析算法，具有闭合解的形式，得到了极其广泛的运用.

迭代法与解析法在一定情况下均会导出较大偏差的目标定位估计值.这是因为无源定位方程是高度非线性的，为了使得方程线性化以便于求解，迭代的定位算法将目标在初始值进行Taylor级数展开，并忽略二阶及二阶以上的噪声项，而具有解析解的两步WLS 定位算法还采用了伪线性化的处理思路，在第一步的WLS过程中，引入了一个与目标定位值相关的中间量，并将其视为与目标独立进行方程求解，导致了更大的偏差值［18］.

目前能够有效减小定位偏差的方法主要有2种，一种是对定位算法的偏差进行估计，再从该算法的定位结果中减去偏差的偏差补偿法［17-22］，该方法在对目标定位偏差实现有效估计的前提下，能够极大地减小目标定位偏差值；另一种是BiasRed 算法［17，22］，该方法通过在定位算法中加入新的约束条件，对定位偏差进行约束，能够将定位偏差值控制在一定的范围内，但由于新增约束条件对噪声敏感，会对定位的方差值造成影响.

针对上述2种方法，考虑到既要最大程度的减小目标的定位偏差，又要尽量小地影响原算法对目标定位的方差值，本文采用偏差补偿法.针对具有解析解的两步WLS定位算法，提出能够有效去除定位偏差，具有闭合解形式的无源定位算法.该算法首先对两步WLS算法在目标定位求解过程中的偏差值进行依次求解，得到最终的偏差值；再从两步WLS算法的定位结果中直接减去该偏差值，得到经过偏差补偿的目标定位解.

1 TDOA／FDOA 无源定位模型

考虑三维空间中的无源定位问题.利用M 个位置和速度准确已知的接收站对目标进行定位.假设各个接收站的位置为si＝［xi，yi，zi］T，速度为＝，i＝1，2，…，M，目标的位置和速度分别为uo＝［x ，y，z ］T和.其中，（＊ ）o表示含噪量（＊ ）的真实值.在三维空间中，需要M≥4个接收站才能完成目标定位，并且所有接收站不在同一条直线上或平面上，才能保证目标定位的唯一性.为了表述方便又不失一般性，假设第一个接收站为基准站.无源定位示意图如图1所示.

图1 无源定位示意图Fig.1 Passive localization scenario

第i个接收站到目标的距离为

为了有效利用FDOA 信息，对式（1）求时间微分可得

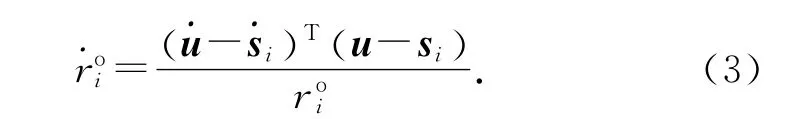
对式（2）求时间微分可得

在实际应用中，TDOA 和FDOA 观测值存在误差，可表示为

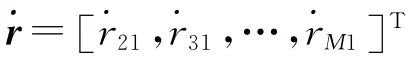
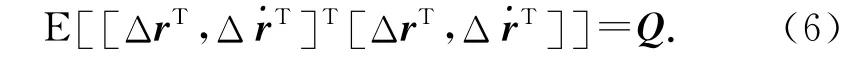
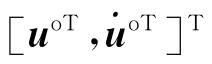
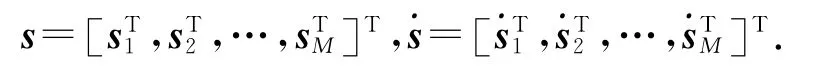
2 TDOA／FDOA 无源定位算法闭合解及其偏差分析

首先对文献［16］所提出的TDOA／FDOA 闭合解形式的定位方法进行介绍.然后，针对该算法，对其定位偏差进行理论分析，得出定位的偏差值.最后，将原定位解减去偏差值的期望，得到一个有效去除定位偏差的新解.

2.1 TDOA／FDOA闭合解

文献［16］所提出的两步WLS算法在三维的情况下，至少需要5个接收站才能实现定位.具体的定位算法可以分为两步加权最小二乘.为了方便后续偏差分析中公式的引用，在此仅罗列两步WLS定位算法中必要的公式，算法的具体推导与实现请参见文献［16］.

1）两步WLS定位算法的第一步结果为

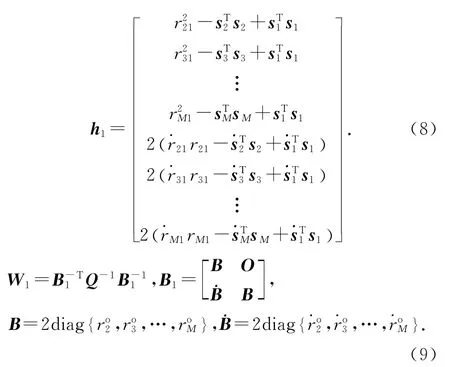
2）第二步：

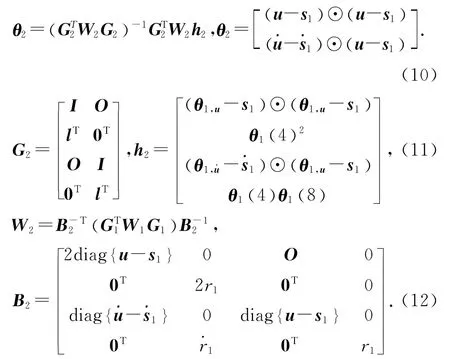
2.2 偏差分析

在偏差分析中，假设为小噪声环境［17］，即测量噪声足够小，二阶以上的噪声项对目标定位精度几乎不产生影响.假设目标不靠近任何一个接收站，确保B1对噪声不敏感［16］.将两步5算法每个步骤的偏差值逐一分析如下.

1）第一步的偏差值Δθ1.

将式（8）中h1、G1的值代入式（13），得

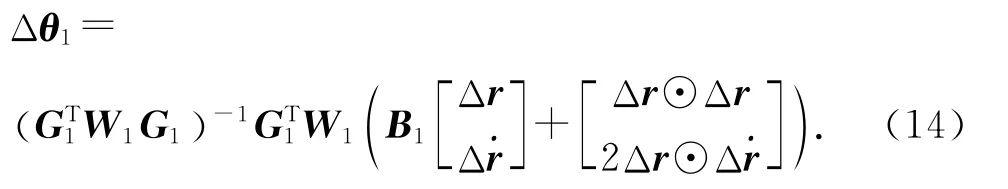
对式（14）求期望，即可求得θ1的理论偏差值.但是，由于G1中含有TDOA 和FDOA 测量噪声，求解的过程将十分复杂.为此，先给出θ1的理论偏差值，将在附录A 中对其进行证明.

定理1 两步WLS算法第一步定位结果θ1的偏差期望值为

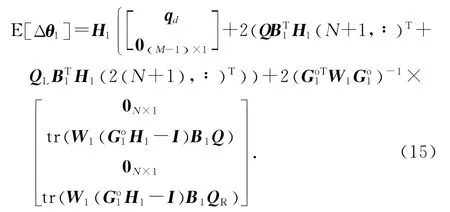
其中，

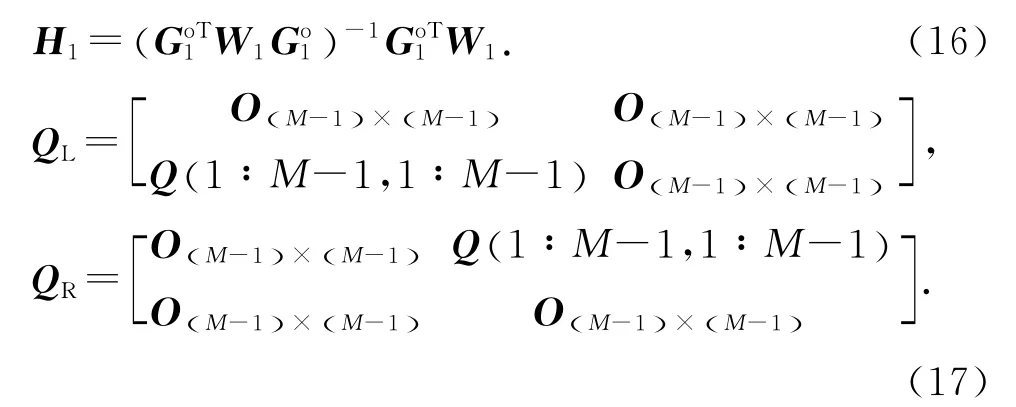
H1（N ＋1，∶ ）和H1（2（ N ＋1） ，∶ ）分 别 表 示H1的 第 N ＋ 1 行 和 第 2 （N ＋1） 行；Q （1∶M-1，1∶M-1） 表示矩 阵Q 的1 到M-1行、1到M-1 列所组成的新矩阵；qd是一个列向量，其元素由Q（1∶M-1，1∶M-1）的对角线元素组成.E ［Δθ1］的 第 一 部 分，H1［qd，0（M-1）×1］，是由于对测量值进行平方处理后，来自回归量h1的二阶噪声分量；剩余部分的偏差来自于从属变量G1中的噪声.

2）第二步的偏差值Δθ2.

在式（10）的左右两边同时减去真实值θo2，得到误差量为

将式（11）代入式（18）得

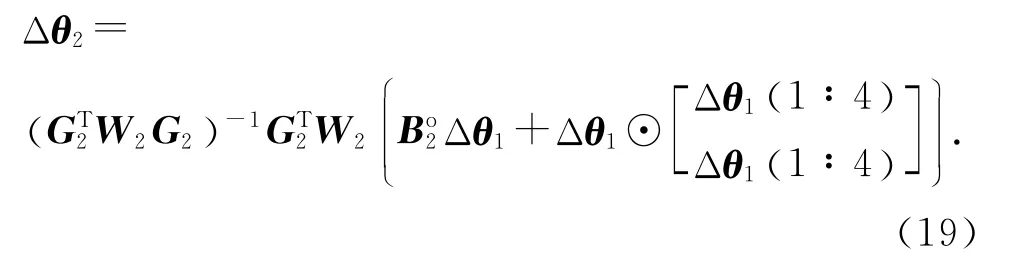
对式（19）求期望，即得到第二步的偏差值.

定理2 两步WLS算法第二步定位结果θ2的偏差期望值为

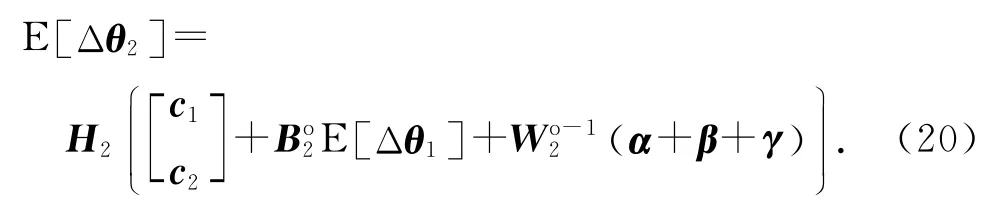
其中，

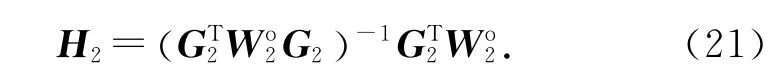
c1和c2都是列向量，其值分别来自于C1（1∶N＋1，1∶N＋1）和C1（1∶N＋1，N＋2∶end）对角线上的元素.C1是θ1的均方误差（mean squares error，MSE）矩阵，表示为

α、β、γ 的值以及定理2的证明将在附录B 中进行详细阐述.

3）总偏差值Δθ.

目标定位的真实值由θo表示，θo可以表示成

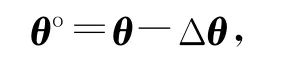
式中：θ为两步WLS估计器对目标位置和速度的估计值，Δθ为目标估计的偏差：

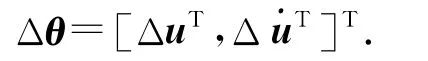
在式（10）中，用uo＋Δu 替换u，用＋替换，用＋Δθ2替换θ2，可得

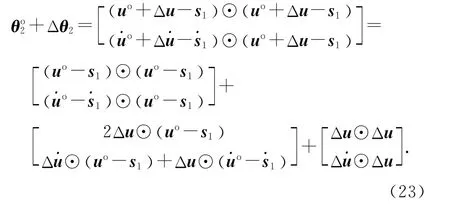
等式的右边分别表示真实值、一阶误差项、二阶误差项，且有

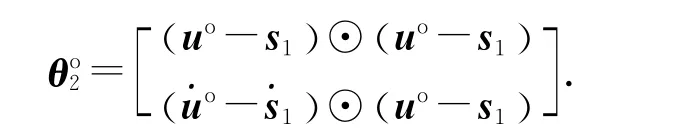
故式（23）可以化为

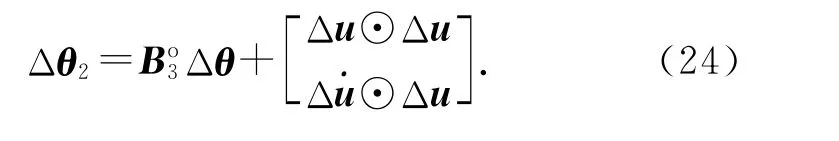
式中：

对式（24）移项整理，得到总的偏差值为

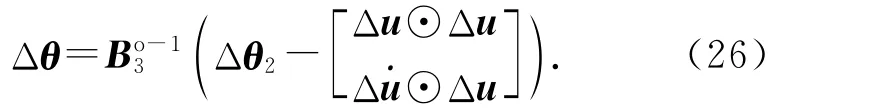
结合式（19）和（26），可得Δθ与Δθ1的关系.

对式（26）取期望得

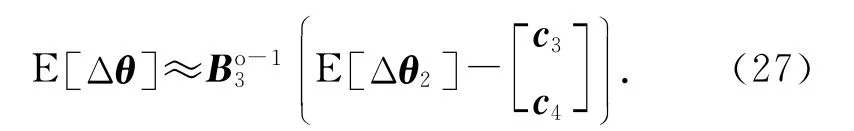
式中：

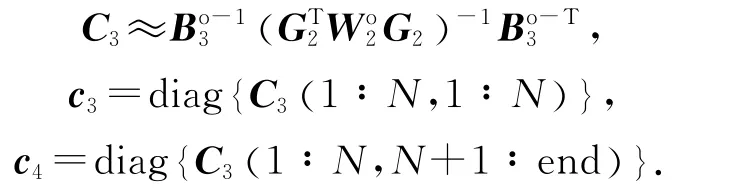
其中，C3是θ的协方差矩阵［16］.

式（27）是两步WLS算法的目标定位理论偏差值.将两步WLS 算法对目标定位的估计值减去其理论偏差值，就得到去除定位偏差后的目标定位结果：

式中：θ表示两步WLS 算法对目标位置和速度的估计值.

在实际的求解偏差过程中，式（27）要用到目标位置和速度的真实值，而这两者是未知数，需要用目标位置和速度的估计值来替换真实值进行计算.

3 定位性能分析

对于参数估计问题，CRLB 为任何无偏估计量的方差确定了一个下限，为无偏估计量的性能提供了标准.将去除定位偏差的TDOA／FDOA 的目标定位估计的协方差与CRLB进行比较.首先证明所提算法的目标定位估计值是无偏的，然后求出目标估计的协方差值，并与CRLB进行比较.

将CRLB的表达式表述如下［16］：

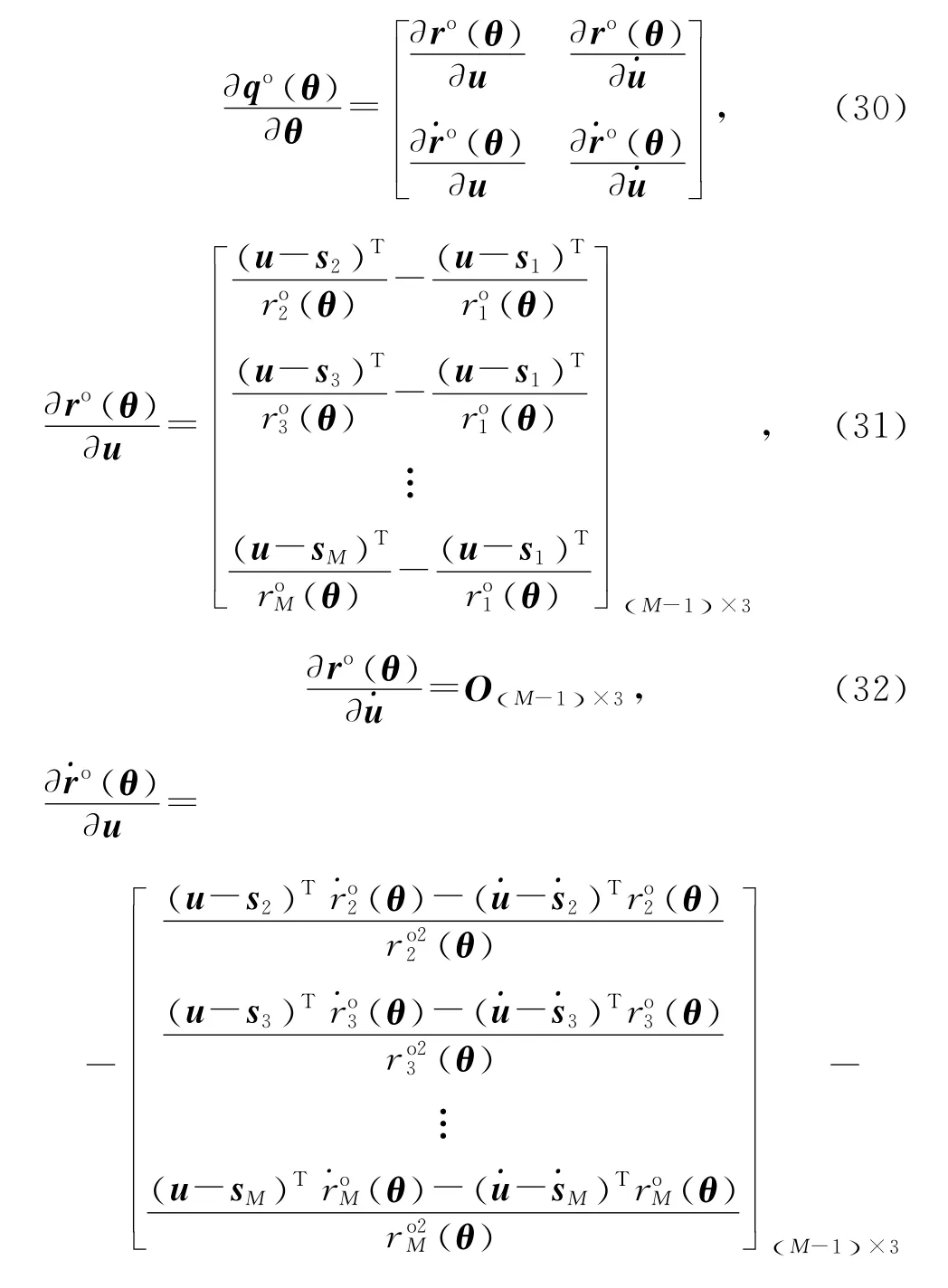
式（29）到（34）详细的证明可以参见文献［16］.

两步WLS算法对目标位置和速度的估计结果可以表示为

将式（35）代入式（28）并取期望得

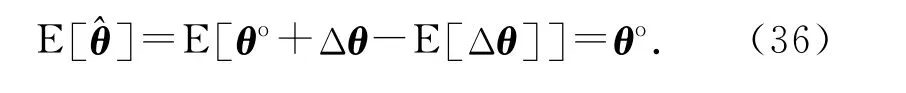
因此，所提出的算法对目标的位置和速度估计是无偏的.

求目标估计的协方差，利用式（28）和（35）可得：

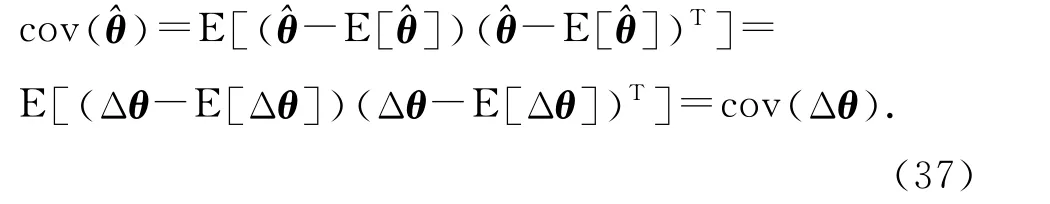
将式（26）、（19）和式（A6）代入式（37），忽略二阶以上的误差统计量得

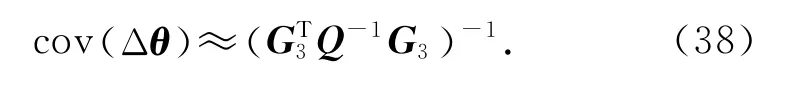
式中：

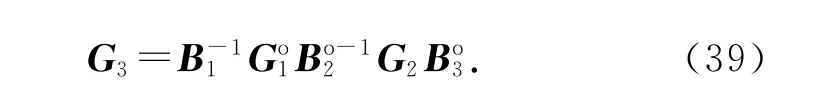
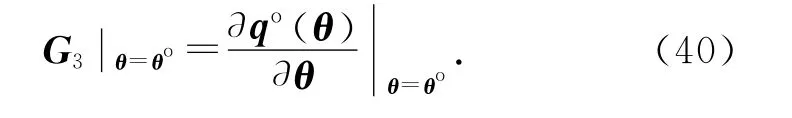
4 仿真实验

为了检验本文所提算法的有效性，进行仿真实验如下.利用6个接收站对目标进行定位，目标位置uo＝ ［2 000，2 500，3 000 ］T，速 度＝［-20，15，40］T.6个接收站的位置和速度如表1所示.

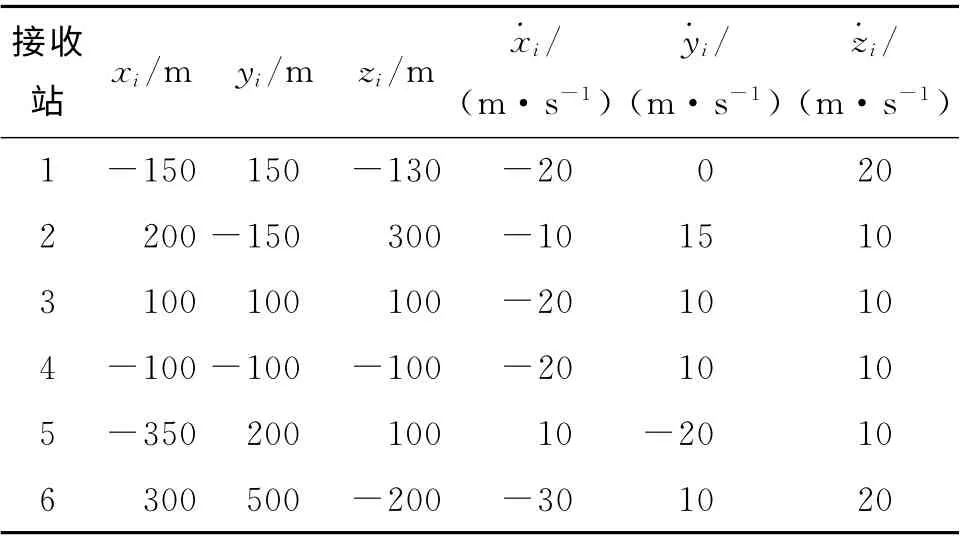
表1 接收站的位置和速度Tab.1Position and velocity of receiver

由于TDOA 测量值与FDOA 测量值分别来自于目标的位置信息和速度信息，两者不相关，假设由目标的TDOA 和FDOA 所组成的测量向量的均值为0，协方差为

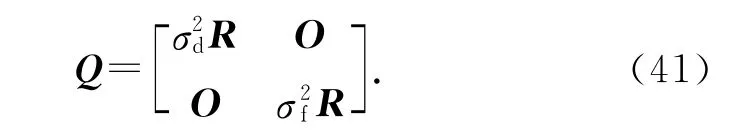
式中：R 的对角元素全部为1，其余元素均为0.5［23］.σd为TDOA 测量误差值，σf为FDOA 测量误差值，并且假设σ2f＝0.01×σ2d［23］.对目标的位置和速度进行L＝10 000次的仿真实验，定位的精度由均方根误差和偏差来衡量，定义为

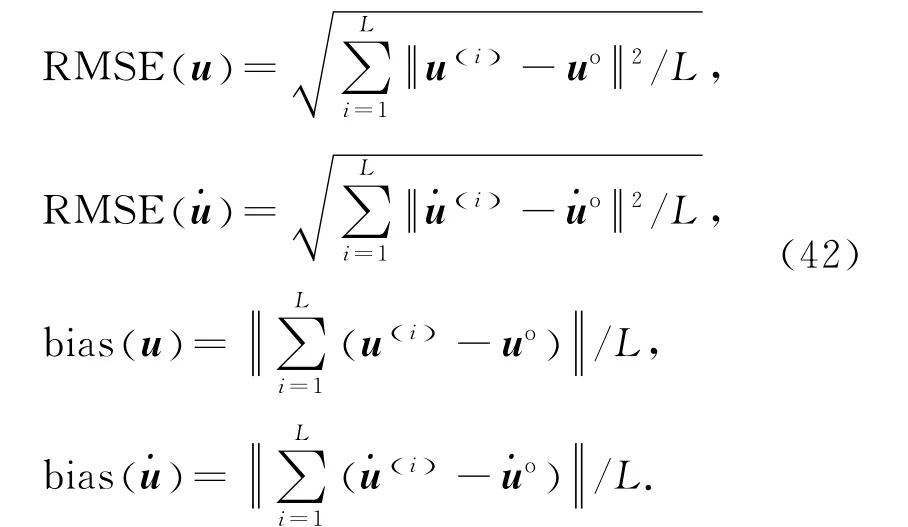
定义TDOA 测量误差值的分贝表示形为

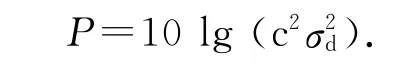
针对目标定位的均方根误差，将两步WLS 算法、Taylor算法、BiasRed算法以及本文所提出的算法进行比较，如图2和3所示.其中，Taylor算法是将目标的真实位置和速度值作为初始值，采用高斯-牛顿迭代法对目标的位置和速度进行估计［15，17］.由仿真结果可得：对于目标的位置估计，当TDOA测量噪声σ2d＜24dB 时，本文所提出的算法仍然能够达到CRLB；当σ2d≥24dB时，随着测量噪声增大，小噪声的假设条件已不再满足，本文所提出的算法与两步WLS算法同时开始偏离CRLB；而BiasRed算法在σ2d＝18dB时已经开始偏离CRLB，这是由于其在原两步WLS算法中加入了新的约束条件，而该条件对噪声较敏感造成的［17］.由于Taylor算法是将目标的真实位置和速度值作为初始值，其定位结果一直接近CRLB.但在实际的定位环境中，初始值的选择往往与真实值存在一定偏差，很可能出现无法收敛的问题.对于目标的速度估计，当TDOA测量噪声σ2d≤18dB 时，上述4种定位算法均达到了CRLB.随着噪声的增大，除了Taylor算法仍接近CRLB外，其余3种算法逐渐开始偏离CRLB，其偏离的原因是由于噪声增大之后，小噪声的假设条件已经不再满足，忽略二阶以上噪声对目标的定位产生了严重的影响.

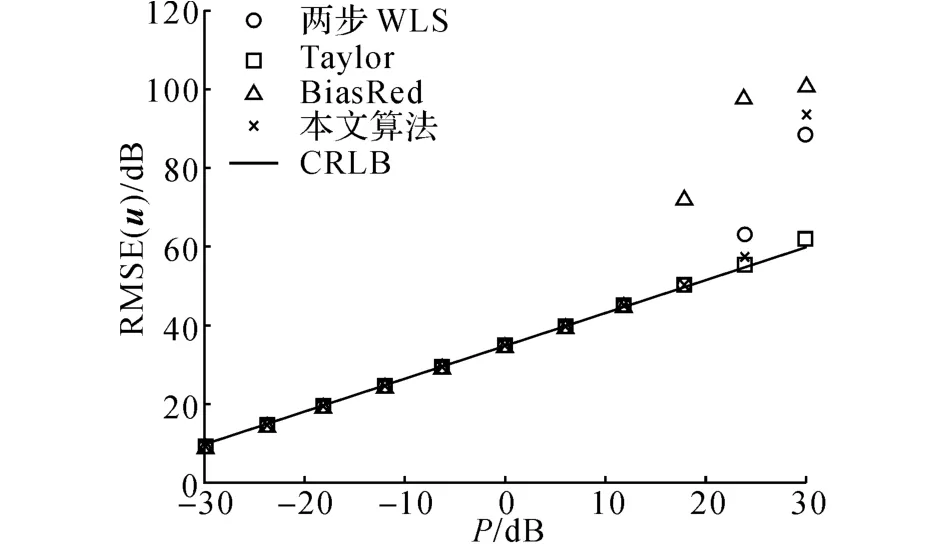
图2 不同定位算法对目标位置估计的均方根误差比较Fig.2 Comparison of RMSEs for source position estimates from different location algorithms

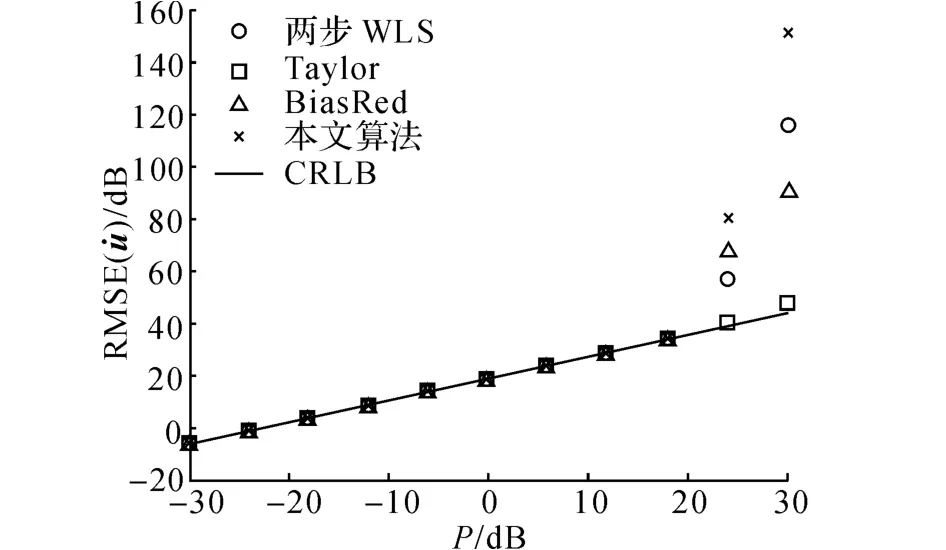
图3 不同定位算法对目标速度估计的均方根误差比较Fig.3 Comparison of RMSE for source velocity estimates from different location algorithms

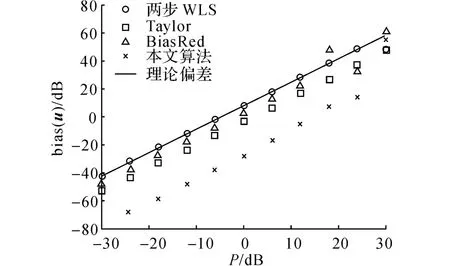
图4 不同定位算法对目标位置估计的偏差比较Fig.4 Comparison of bias for source position estimates from different location algorithms

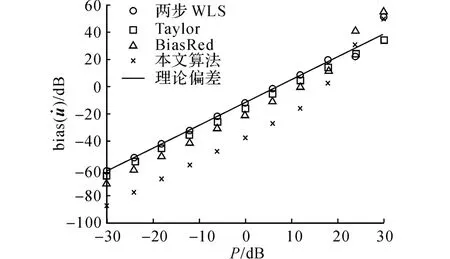
图5 不同定位算法对目标速度估计的偏差比较Fig.5 Comparison of bias for source velocity estimates from different location algorithms

针对目标定位的偏差，将两步WLS算法、Taylor算法、BiasRed算法以及本文所提出的算法进行比较，如图4和5所示.由仿真结果可得：1）当小噪声假设仍然适用时，即当本文所提出的算法未偏离CRLB时，两步WLS算法偏差的理论分析值与实际偏差值基本一致，证明本文所提出的方法能对两步WLS算法的偏差值进行准确估计；2）当噪声足够小、4种算法的RMSE值都能达到CRLB时，Taylor算法的目标位置和速度估计偏差值分别比两步WLS算法的偏差值小12dB 和4dB 左右，这是由于两步WLS算法在求解过程中进行伪线性化处理以及WLS估计器中的回归量h1与从属变量G1中的噪声相互交迭造成的［17］；3）当噪声足够小、4 种算法的RMSE值都能达到CRLB时，本文所提出的算法对目标的位置估计偏差比两步WLS算法要小35dB 左右，比Taylor算法小20dB 左右，比BiasRed算法小30dB左右；对目标的速度估计偏差，比两步WLS算法要小25dB 左右，比Taylor算法要小20dB左右，比BiasRed算法小15dB左右.这是由于在上述4种算法中，两步WLS算法和Taylor算法并没有进行定位偏差抑制方面的处理，其定位偏差程度较大；BiasRed算法是在两步WLS算法的基础上，加入新的约束条件，对第一步的偏差Δθ1进行抑制［17］，忽略了第二步的偏差Δθ2对总偏差的影响，其偏差程度较原两步WLS算法会有所改善.本文所提出的算法是先对两步WLS算法的目标定位偏差值进行估计，再从原估计值中减去总的偏差值，在噪声较小、偏差估计准确的情况下，本算法能够最大程度地去除定位偏差.

5 结 语

相比于迭代法，本文提出的去除偏差的具有闭合解形式的TDOA／FDOA 定位算法无需初始值的估计，不存在收敛的问题.经仿真实验验证，在远距离目标和小噪声的条件下，本文算法算法与Taylor算法、两步WLS 算法和BiasRed算法保持同等程度的定位方差，而该算法的定位偏差远远小于其余3种算法，证明该算法能够有效的去除定位偏差，提高目标的定位精度.在下一步的研究中，将会进一步考虑在接收站自身的位置和速度参数存在误差条件下的目标定位偏差去除问题.

（

）：

［1］YU H G，HUANG G M，GAO J.Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties［J］.IET Radar，Sensor and Navigation，2012，6（9）：891-899.

［2］LUO J，WALKER E，Bhattacharya P，et al.A new TDOA／FDOA-based recursive geolocation algorithm ［C］∥Proceeding of SSST.Texas：IEEE，2010：208-212.

［3］MUSICKI D，KAUNE R，KOCH W.Mobile emitter geolocation and tracking using TDOA and FDOA measurements［J］.IEEE Transactions on Signal Processing，2010，58（3）：1863-1874.

［4］HO K C，Lu X，Kovavisaruch L.Source localization using TDOA and FDOA measurements in the presence of receiver location errors：analysis and solution ［J］.IEEE Transactions on Signal Processing，2007，55（2）：684-696.

［5］郭福成.基于多级网格搜索的固定单站无源定位方法［J］.信号处理，2008，24（6）：927-930.GUO Fu-cheng.A fixed observer passive location method based on multi-level grid search［J］.Signal Processing，2008，24（6）：927-930.

［6］常飞，武小悦.基于改进粒子群算法的卫星数传任务调度［J］.系统工程与电子技术，2009，31（10）：2404-2408.CHANG Fei，WU Xiao-yue.Satellite data transmission task scheduling based on advanced particle swarm optimization ［J］.Systems Engineering and Electronics，2009，31（10）：2404-2408.

［7］刁鸣，袁熹，高洪元，等.一种新的基于粒子群算法的DOA 跟踪方法［J］.系统工程与电子技术，2009，31（9）：2046-2049.DIAO Ming，YUAN Xi，GAO Hong-yuan，et al.New method of estimating direction-of-arrival of moving sources based on particle swarm algorithm ［J］.Systems Engineering and Electronics，2009，31（9）：2046-2049.

［8］牛江川，刘明杰，宋荣昌，等.基于量子粒子群算法的惯性保险机构优化设计［J］.北京理工大学学报，2009，29（11）：959-963.NIU Jiang-chuan，LIU Ming-jie，SONG Rong-chang，et al.Optimization design of the inertia sagety mechanism based on QPSO algorithm ［J］.Transactions of Beijing Institute of Technology，2009，29（11）：959-963.

［9］罗航，王厚军，黄建国，等.基于PSO 的三参数威布尔分布参数的联合估计方法［J］.仪器仪表学报，2009，30（8）：1604-1612.LUO Hang，WANG Hou-jun，HUANG Jian-guo，et al.Method of united estimation to the parameters of three-parameter Weibull distribution based on PSO［J］.Chinese Journal of Scientific Instrument， 2009，30（8）：1604-1612.

［10］SUN J，XU W B.A global search strategy of quantumbehaved particle swarm optimization［C］∥Proceedings of IEEE conference on Cybernetics and Intelligent Systems.Singapore：IEEE，2004：111-116.

［11］SUN J，FENG B，WU W H.Particle swarm optimization with particles having quantum behavior［C］∥Proceedings of 2004Congress on Evolutionary Computation.［S.l.］：IEEE，2004：325-331.

［12］吴林晟，周希朗，高为，等.一种基于改进遗传算法的只测向无源定位技术［J］.电子与信息学报，2006，28（12）：2252-2255.WU Lin-sheng，ZHOU Xi-lang，GAO Wei，et al.A bearing-only passive location method based on improved genetic algorithm［J］.Journal of Eletronics and Information Technology，2006，28（12）：2252-2255.

［13］赵光权，彭喜元，孙宁.带局部增强算子的微分进化改进算法［J］.电子学报，2007，35（5）：849-853.ZHAO Guang-quan，PENG Xi-yuan，SUN Ning.A modified differential evolution algorithm with local enhanced operator［J］.Acta Electronica Sinica，2007，35（5）：849-853.

［14］张晓伟，刘三阳.免比例因子F的差分进化算法［J］.电子学报，2009，36（6）：1318-1323.ZHAO Xiao-wei，LIU San-yang.Differential evolution without the scale factor F［J］.Acta Electronica Sinica，2009，36（6）：1318-1323.

［15］常彦鑫，高正红.自适应差分进化算法在气动优化设计中的应用［J］.航空学报，2009，30（9）：1590-1596.CHANG Yan-xin，GAO Zheng-hong.Application of adaptive differential evolutionary algorithms to aerodynamic optimization design［J］.Acta Aeronautica et Astronautica Sinica，2009，30（9）：1590-1596.

［16］LU X，HO K C.Taylor-series technique for moving source localization in the presence of sensor location errors［C］∥in Proceedings on 2006IEEE International Symposium on Circuits and Systems，Island of Kos：IEEE，2006：1075-1078.

［17］HO K C，XU W.An accurate algebraic solution for moving source location using TDOA and FDOA measurements［J］.IEEE Transactions on Signal Processing，2004，52（9）：2453-2463.

［18］HO K C.Bias reduction for an explicit solution of source localization using TDOA ［J］.IEEE Transactions on Signal Processing，2012，60（5）：2101-2114.

［19］周成，黄高明，单鸿昌，等.基于最大似然估计的TDOA／FDOA 定 位 偏 差 补 偿 算 法［J］.航 空 学 报，2015，36（3）：979-986.ZHOU Cheng，HUANG Gao-ming，SHAN Hongchang，et al.Bias compensation algorithm based on maximum likelihood estimation for passive localization using TDOA and FDOA measurements［J］.Acta Aeronautica et Astronautica Sinica，2015，36（3）：979-986.

［20］WANG P，JI Y M，ABHAYAPALA T.Bias analysis and reduction for underwater localization problem ［C］∥Proceedings of the 31st Chinese Control Conference，Hefei：IEEE，2012：5178-5182.

［21］CHEN H，LIAN F.Bias estimation for multiple passive sensors ［C］∥20121ntemational Conference on Measurement，Information and Control（MIC），Harbin：IEEE，2012：1081-1084.

［22］JI Y M，YU C B，ANDERSON B D O.Bias-correction in localization algorithms［C］∥2009Global Telecommunications Conference，Honolulu：IEEE，2009，11：1-7.

［23］HAO B J，LI Z，QI P H，et al.Effective bias reduction methods for passive source localization using TDOA and GROA［J］.SCIENCE CHINA Information Sciences，2013，56（7）：1-12.

［24］WANG G，LI Y M，ANSARI N.A semidefinite relaxation method for source localization using TDOA and FDOA measurements［J］.IEEE Transaction on Vehicular Technology，2013，62（2）：853-862.

［25］MOON T K，STIRLING W C.Mathematical Methods and Algorithms for Signal Processing［M］.New Jersey：Prentice-Hall，2000.

附录A 定理1的证明

假设P1＝W1G1，代入式（14）得

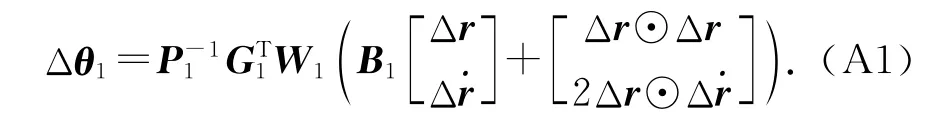
G1可以表示为

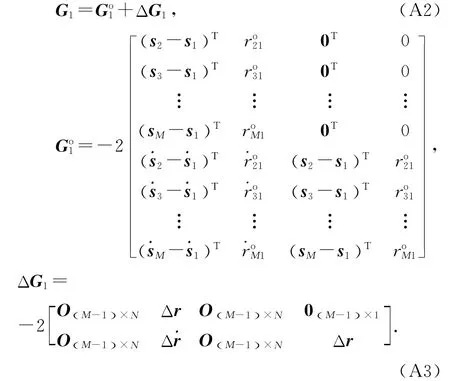
将式（A2）代入P1＝W1G1得

式中：P1含有的二阶噪声统计量W1ΔG1，其与相乘之后将产生二阶以上的噪声项，在本文所假设的小噪声环境下，其对目标定位的影响可以忽略不计.同时，在小噪声环境下，根据Neumann展开［24］，有

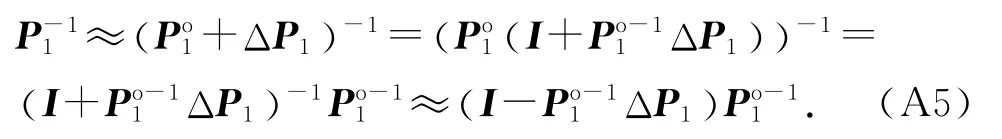
将式（A2）和（A5）代入式（A1），在小噪声环境下，忽略二阶以上的误差统计量，得

利用式（A3）和迹的等式yTAx＝tr （Ax yT）得

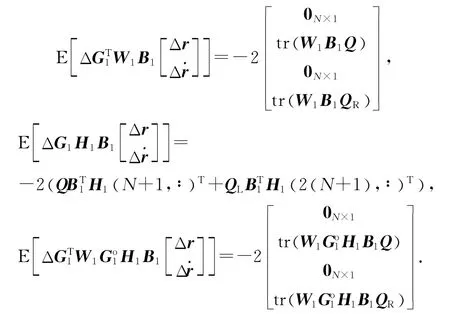
将式（A4）、（A5）代入式（A6），并取期望，即得到式（15）.证毕.

附录B 定理2的证明

尽管G2是常量，但是由于W2中有含噪量B2和G1，应将其展开成包含噪声项Δr、Δ˙r、Δθ1表达的形式.B2可以写成如下形式：

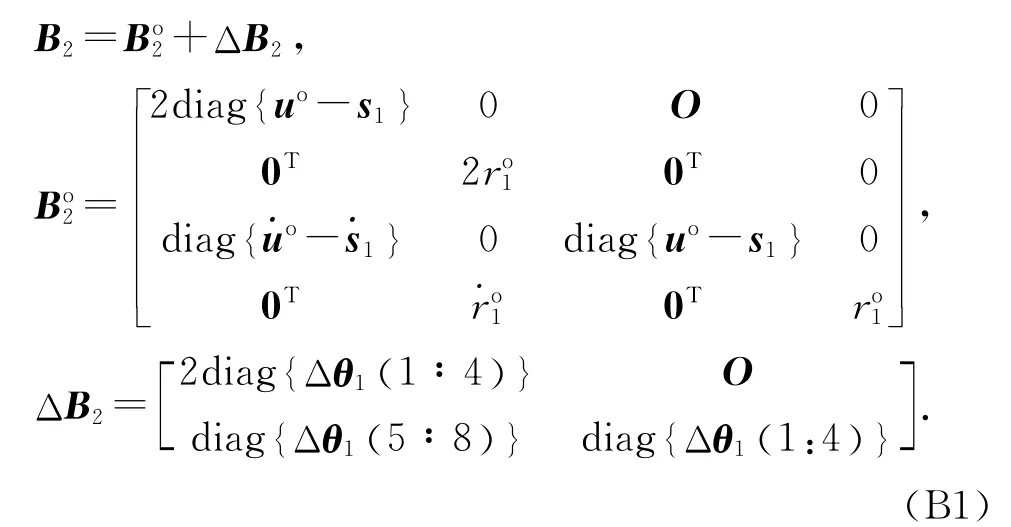
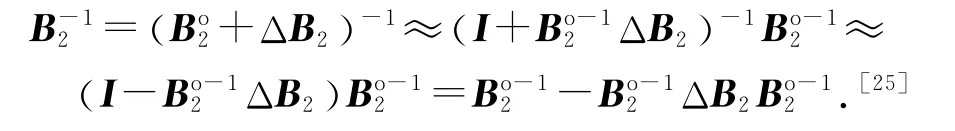
将式（A4）和（B1）代入式（12），忽略高于二阶的噪声统计量，得W2≈Wo2＋ΔW2，

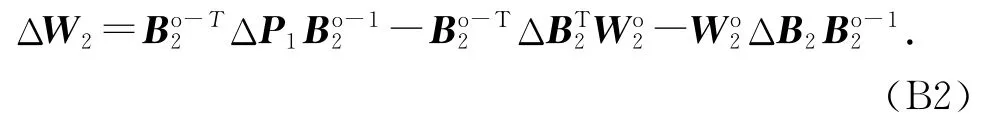
为了表达方便，令P2＝W2G2，故有

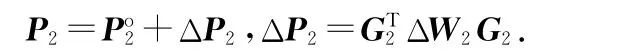
在小噪声的假设条件下，Po-12ΔP2≈O，同样有

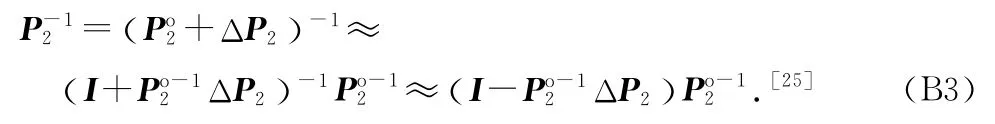
将式（B3）代入式（19），忽略高于二阶的误差统计量，可得θ2的偏差为

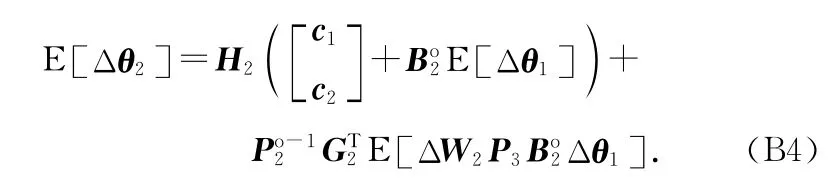
式中

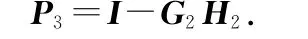
代入式（B2），可得

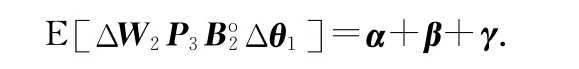
利用式（A4）和（A6），忽略高于二阶的误差统计量，并利用迹的等式yTAx＝tr （Ax yT），α 的值可以表示为

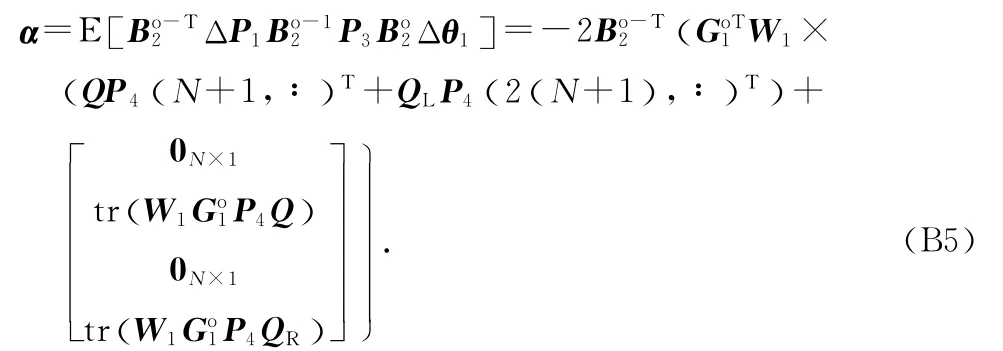
其中，

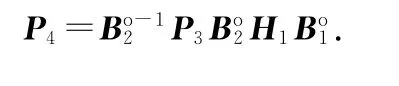
利用式（B1），可得

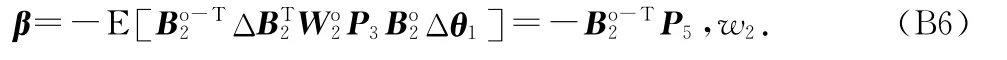
式中：P5＝P3Bo2，P5W ＝Wo2P5.P5W 与C1具有相同的维度，可以划分为分块矩阵如下

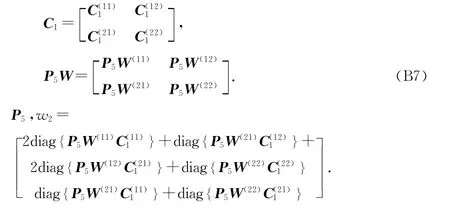
利用式（B1），可得

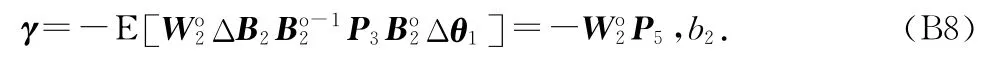
式中：P5B＝Bo-12P5.P5B 与C1具有相同的维度，可以划分为分块矩阵如下

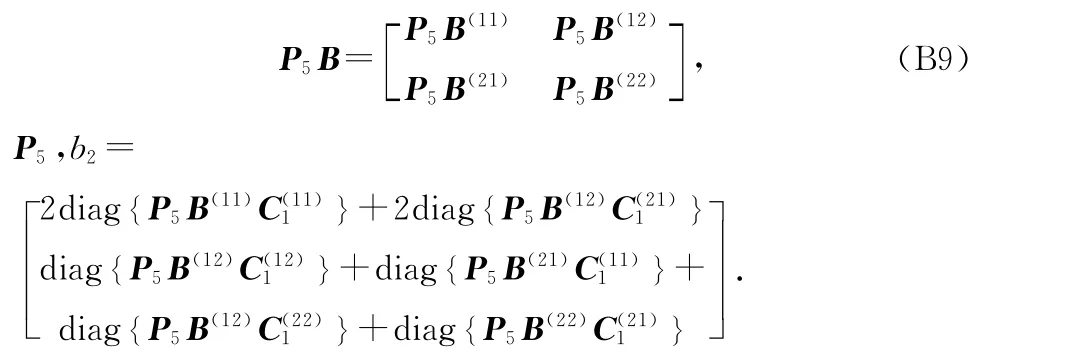
将式（15）、（B5）、（B6）、（B8）代入式（B4），即得到θ2的偏差值表达式（20）.证毕.