基于OpenMP的并行粒子群优化算法研究
2015-07-07康军广段国林王金敏田永军
康军广,段国林,王金敏,田永军
(1.河北工业大学机械工程学院,天津 300130;2.天津职业技术师范大学机械工程学院,天津 300222)
基于OpenMP的并行粒子群优化算法研究
康军广1,段国林1,王金敏2,田永军1
(1.河北工业大学机械工程学院,天津 300130;2.天津职业技术师范大学机械工程学院,天津 300222)
针对现有粒子群优化算法多采用串行方式执行且运行效率较低的问题,提出一种基于OpenMP技术的并行粒子群优化算法.该算法以多核硬件平台为基础,利用粒子群算法搜索速度快,易于并行等特点,引入OpenMP技术,通过将该并行算法应用于布局问题求解并与串行算法相比较,测试结果表明,该并行算法与串行算法结果一致,能够充分利用多核CPU的计算资源,运行效率得到明显提高.
OpenMP;并行;粒子群;多核CPU
粒子群优化算法(Particle Swarm Optim ization,PSO)是一种基于群体智能的启发式全局优化方法,具有结构简单、参数少、收敛速度快、易于实现并行等优点,近年来受到学术界的广泛关注,目前已应用于函数优化、TSP问题、布局问题、神经网络训练、工业系统优化与控制、系统辨识等诸多领域[1].然而粒子群优化算法多是基于串行方式执行的,不能充分利用现有的多核CPU硬件平台,造成过多的程序运行等待时间.
随着多核CPU的普及,目前主流计算机均配置为多核CPU,并配有大容量内存.如何让原有串行执行的程序在多核CPU下高效并行执行,是目前急需解决的问题.有效解决这个问题的方法之一就是利用多核并行计算技术,在算法的执行过程中,将程序任务下发给多个处理器核心,让多个核心同时去处理,并返回最终结果,有效提高每个处理器核心的利用率.OpenMP是共享内存并行程序设计的工业标准,支持C、C++以及Fortran等编程语言,具有良好的可移植性,适合于共享内存的多核计算机,可以方便的通过编译指导语句将串行程序改造成并行执行[2].本文在分析粒子群算法和OpenMP并行技术实现细节的基础上,实现了基于OpenMP技术的并行粒子群算法,并将并行粒子群算法应用于矩形布局问题求解,验证了该并行粒子群算法的可行性和高效性.
1 粒子群算法
粒子群优化算法是由美国社会心理学家Kennedy和电气工程师Eberhart于1995年提出的一种基于群智能的演化计算技术[3-4],粒子群优化算法通过群体中粒子间的合作与竞争产生的群体智能来指导优化搜索.与演化计算相比,PSO算法保留了基于种群的全局搜索策略,它采用的速度—位移模型操作简单,避免了复杂的遗传操作.粒子群算法特有的记忆功能,使其可以动态跟踪当前的搜索情况,调整其搜索策略,是一种高效的并行搜索算法.
1.1 算法原理
粒子群优化算法采用“群体”与“进化”的概念,依据个体(微粒)的适应值大小进行操作,粒子群优化算法不像其它进化算法那样对于个体使用进化算子,而是将每个个体看做是在D维搜索空间的一个没有重量和体积的微粒,并在搜索空间中以一定的速度飞行,该飞行速度随个体的飞行经验和群体的飞行经验进行动态调整[5].
设Xi=χi1,χi2,,χiDT为微粒i的当前位置;Vi=vi1,vi2,,viDT为微粒i的当前飞行速度;Pi=pi1, pi2,,piDT为微粒i所经历的最好位置,也就是微粒i所经历过的具有最好适应值的位置,称为个体最好位置.粒子通过跟踪2个“极值”来更新,第1个“极值”为粒子本身所找到的最好解,称为个体最优,其位置用pbest表示.第2个“极值”为整个粒子群中所找到的最好解,称为全局最优,其位置用gbest表示.粒子群算法的进化方程可描述为:
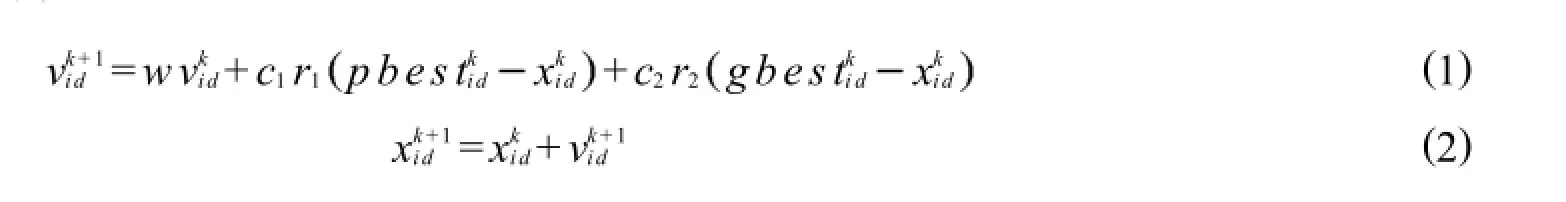
其中:χkid是粒子i在第k次迭代中第D维的位置,W为惯性权重,用来控制算法的开发和探索能力;c1、c2为加速系数,通常在0~2之间取值,分别调节个体向自身最好位置和全局最好位置方向飞行的最大步长;r1、r2为0,1之间的随机数,为了减少在进化过程中,微粒离开搜索空间的可能性,vijvmax,vmax.如果问题的搜索空间限定在χmax,χmax内,则可设定vmax=kχmax,0.1k1.0.
1.2 粒子群算法流程
本文将粒子群算法用于对矩形布局问题求解过程中定位函数的优化[6],其中,定位函数包含多个参数,每个参数的取值范围均为[0,1],每个粒子位置对应定位函数中某个参数的一组取值,通过粒子位置的更新找到种群中粒子的最优位置gbest,gbest为满足定位函数值最小的粒子位置,即满足定位函数要求的参数最优值,具体算法流程如下:
1)初始化粒子群,随机产生满足条件的粒子的位置和速度,并确定粒子的pbest和gbest;2)对每个粒子,将它的当前位置与它的pbest进行比较,如果是当前位置更好,则将其作为当前最好位置pbest,否则,pbest保持不变;3)对每个粒子,将它的当前位置和群体中的gbest比较,如果这个粒子的位置更好,则将其设置为当前的gbest,否则,gbest保持不变;4)更新粒子的速度和位置;5)如未达到终止条件,则转步骤2);6)开始下一轮迭代计算,否则取当前gbest为最优解;7)将gbest的值赋值给定位函数中的各个参数,确定待布矩形的布入位置.
2 粒子群算法并行化实现
OpenMP的执行模型采用fork-join的形式[7],其中fork创建新线程或者唤醒已有线程,join即多线程的会合.Fork-join执行模型在刚开始执行的时候,只有一个称为“主线程”的运行线程存在.主线程在运行过程中,当遇到需要进行并行计算的时候,派生出线程来执行并行任务.在并行执行的时候,主线程和派生线程共同工作,在并行代码执行结束后,派生线程退出或者阻塞,不再工作,控制流程回到单独的主线程中.
粒子群优化算法主要包括对种群中所有个体的位置和速度的初始化,选出局部最优解和全局最优解,通过速度、位置更新公式对所有个体进行更新迭代得到新的位置和速度.无论是个体的初始化,还是个体的位置和速度的更新,都是通过大量循环迭代实现的,是整个算法运行过程中最耗费时间的部分.循环并行化是使用OpenMP并行化程序的最重要部分,在OpenMP编程模式下,使用编译指导语句能将循环中工作分配到一个线程组中,线程组中的每一个线程分担循环中的一部分内容,实现整个程序的并行化,种群中粒子位置、速度初始化并行实现如图1所示.
OpenMP对循环并行化语句有严格的格式限制,循环变量必须是整数,而且在循环开始必须明确循环变量的初始值,结束条件和递增值.而且循环语句应该是单入口单出口的,在循环过程中不能出现break、goto语句.由于OpenMP只支持for循环的任务分担,需要将原有算法中的do-while循环改造成for循环格式,当循环次数比较小时,由于创建线程会占用一部分开销,并行效率并不高,有时可能会因为线程的创建开销增加程序运行时间,不适合改造成并行执行.
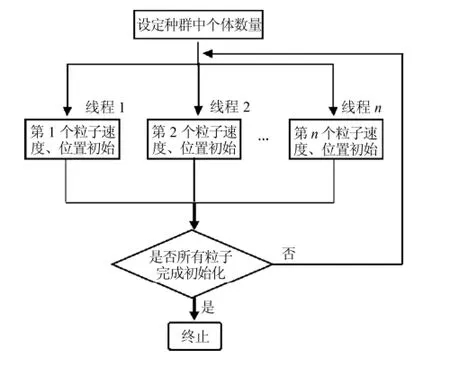
图1 粒子位置、速度初始化Fig.1 Initializationof the individuals'positionsand speeds
由于多线程同时执行循环语句中的代码,这就会出现数据的作用域问题,作用域用来控制某一个变量是否是在各个线程之间共享或者是某一个线程是私有的数据的作用域子句用shared来表示一个变量是各个线程之间共享的,用private来表示一个变量是每一个线程私有的,默认的变量作用域是共享的,在粒子群算法循环并行化之前要明确并行语句块中哪些变量应该设置为private,哪些设置为shared.
并行粒子群优化算法中每代粒子更新操作分散到多个线程同时执行,每次循环需要调用适应值函数,计算当前粒子的适应值,然后更新当前粒子的最优位置和整个种群的最优位置,整个种群的最优位置为全局变量,如果多个线程同时更新全局最优位置,这将会出现变量的读写冲突,通过#pragma omp critical编译制导语句可以解决该问题,当程序中的某一线程执行到#pragma omp critical里面时,要查看有没有其它线程正在里面执行,如果有的话,要等其它线程执行完再进去执行.这样就避免了数据读写冲突问题,但显而易见,它的执行速度会变低,因为可能存在线程等待的情况.粒子位置、速度更新并行程序如下:
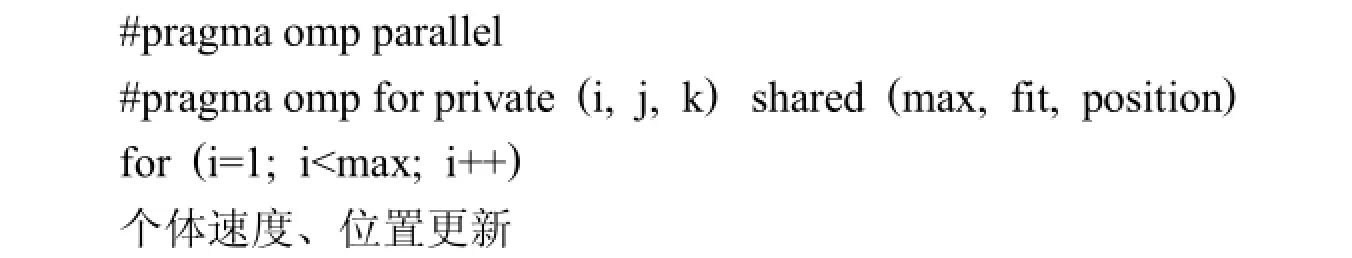

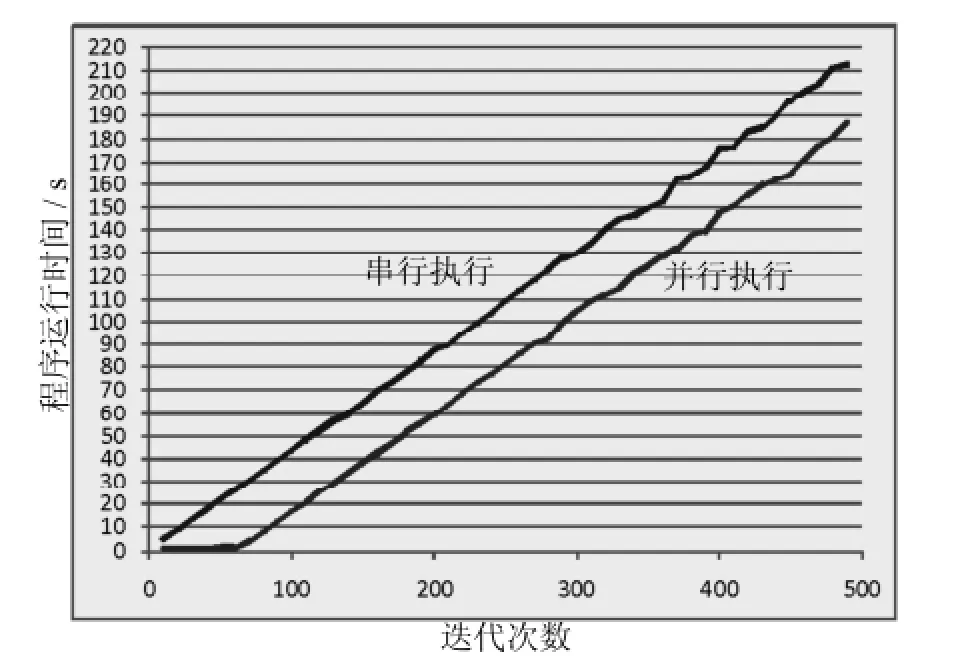
图2 不同迭代次数下串行和并行运行时间Fig.2 Running time of sequentialand parallelized way
3 实验结果与分析
为了验证算法的有效性,本文将并行粒子群算法用于矩形布局问题求解,并行算法和串行算法进行比较.为了使所得结果具有可比性,2种算法均运行在同一台计算机上,计算机配置为Intel Core i7-2600,4G内存,操作系统为32位w indows7,软件为VSStudio 2008.选取同一个矩形布局问题进行测试,通过OpenMP的库函数omp-setthreads()动态设置程序在并行运行过程中创建线程的数量.在改变种群的迭代次数和创建的线程数以后,并行程序运行时间比串行程序明显降低,如图2所示,当程序迭代次数在60次以内时,并行运行时间大约在1 s左右,而串行执行时间随着循环迭代次数的增加呈直线增长,并行效率非常明显,但当迭代次数大于60次以上并小于500次时,串行运行时间和并行运行时间基本保持相等的间距,随着迭代次数增加和线程数的不断增加,并行程序运行时间和串行程序运行时间的差距逐渐变小,如图3所示,当迭代次数在1400次时,并行运行时间和串行运行时间基本相等,此时并行效果很差.
图4为当循环迭代次数固定,随着创建的线程数的增加,并行程序执行时间变化图.从图中可以看出,创建的线程数增多会降低程序运行时间,因为循环块中的代码由更多的线程去同时处理,但创建的线程数达到循环规模一般以后,程序运行时间不再改善,维持在一个值附近波动,出现这种结果的原因是过多的创建线程会导致大量系统时间开销,线程之间数据的访问也会占用额外开销,从而会抵消程序的并行效率,在将串行程序改造成并行方式时要仔细分析程序中每次循环的计算规模和PC机的性能,灵活的设置创建的线程数,充分利用多核CPU的计算能力.
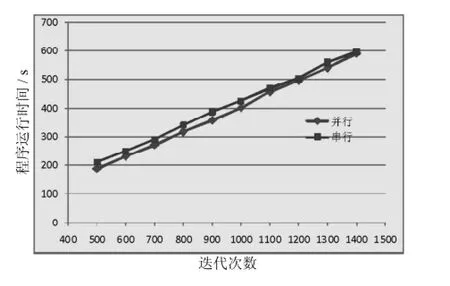
图3 迭代次数为500次以上串行并行运行时间Fig.3 Running tim eofabove500 iterations

图4 不同迭代次数和不同线程数下程序运行时间Fig.4 Running time ofdifferent iterationsand threads
4 结论
本文针对现有粒子群优化算法多采用串行方式执行且运行效率较低的问题,对串行粒子群算法进行分析,提出了一种基于OpenMP的并行粒子群优化算法.通过将该并行算法应用于矩形布局问题求解,并与串行算法相比较.实验结果表明,本文提出的并行粒子群算法合理可行,并行算法充分利用现有计算机多核处理器的资源,提高了求解矩形布局问题的速度,为求解大规模布局问题提供了参考.
[1]Bratton D,Kennedy J.Definingastandard forparticlesw arm optim ization[C]//Proceedingsof the IEEESwarm IntelligenceSymposium.Honolulu,HI,2007:120-127.
[2]Barbara C,Gabriele J.UsingOpenMP[M].London:TheM IT Press,2007.
[3]Kennedy J,EberhartR.Particleswarm optimization[C]//IEEE InternationalConferenceon NeuralNetwork-s,Perth,Australia,1995:1942-1948.
[4]姜建国,田旻,王向前,等.采用扰动加速因子的自适应粒子群优化算法[J].西安电子科技大学学报,2012,39(4):74-80.
[5]Qi Yang,Wang Jinmin.The particle swarm optimization algorithm for solving rectangular packing probl em[J].Advanced materials research,2011,186:479-483.
[6]王金敏,杨维嘉.动态吸引子在布局求解中的应用[J].计算机辅助设计与图形学学报,2005,17(8):1725-1730.
[7]盛楠,廖成,张青洪,等.基于OpenMP的多辐射源二维电波传播预测方法[J].电波科学学报,2013,28(4):611-615.
[责任编辑 杨屹]
Research on parallelparticle swarm optimization algorithm based on OpenMP
KANG Junguan1,DUANGuolin1,WANG Jinmin2,TIAN Yongjun1
(1.SchoolofMechanical Engineering,HebeiUniversity of Technology,Tianjin 300130,China;2.SchoolofM echanicalEngineering, Tianjin University of Technology and Education,Tianjin 300222,China)
Concerning the low performanceand executing in sequentialway ofmostparticle swarm optim ization algorithms,a parallelalgorithm based on OpenMPwasproposed.By introducingOpenMPtechnology,thealgorithm w ith the advantages of searching fastand easy to be parallelized of PSO isbased onmulti-core hardware platform.The parallel particleswarm algorithm is tested by solving the rectangular layoutinstance and iscomparedw ith thesequentialway.The experimental resultsw egotare the same asby choosing the sequentialway,also the results show that the proposed algorithm hasim proved the efficiency insolving the rectangular layoutproblem bymaking fulluse of themulticore com puting resources.
OpenMP;parallel;PSO;multi-coreCPU
TP301.6
A
1007-2373(2015)02-0034-04
10.14081/j.cnki.hgdxb.2015.02.008
2014-07-11
国家自然科学基金(60975046)
康军广(1981-),男(汉族),博士生.通讯作者:段国林(1963-),男(汉族),教授,博士生导师.
数字出版日期:2015-04-16数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20150416.1046.006.html
