基于T-S模型的复杂非线性大系统有限时间分散控制
2015-07-07杨德东蔡玉柱
杨德东,蔡玉柱
(河北工业大学控制科学与工程学院,天津 300130)
基于T-S模型的复杂非线性大系统有限时间分散控制
杨德东,蔡玉柱
(河北工业大学控制科学与工程学院,天津 300130)
利用模糊控制方法研究了复杂非线性大系统的有限时间分散控制问题.基于T-S模型给出了复杂非线性大系统的数学描述,设计了有限时间分散模糊控制器.给出了保证闭环系统有限时间稳定(FTS)的充分条件,该条件可以表示为线性矩阵不等式(LMI)形式,数值例子表明了所提出方案的有效性.
大系统;有限时间稳定(FTS);分散控制;模糊控制;T-S模型
0 引言
自从20世纪70年代初期,《Nature》报道复杂大系统相关问题以来[1-2],该方向的研究始终是国内外学者研究的重点和热点所在.由于复杂大系统的规模庞大,结构复杂,因此传统的集中控制技术已不再适用,从而更多的采用分散控制方式[3].复杂大系统研究的近期总结与回顾可见综述文献[4],从中不难发现Lyapunov稳定性理论是分析与综合技术的核心,得到的结果常常是闭环系统渐近稳定.虽然具有理论上的效果,但在实际工业生产中渐近稳定并不一定是要追求的唯一结果,例如:在化工生产过程中某一时间段要求状态不能偏离平衡点超过一定的界限.渐近稳定对于复杂大系统来说有时也略显保守,由于系统的复杂性,有可能这样的解不能存在,并且也不是必要的,例如:常常由于噪音信号的存在使得最终状态输出受到干扰从而在平衡点附近波动.连续时间线性系统有限时间稳定(FTS)的概念在文献[5]中被给出,目的是为了拓展Lyapunov稳定结果,此后得到了推广[6-7].针对连续时间非线性系统的FTS问题,文献[8-9]提供了一些有价值的结果.
实际中大系统常常表现为典型的非线性特征,并具有较高的状态维数和复杂的拓扑结构,难以建立精确的数学模型,所以从一开始,智能控制技术就较早的应用到该领域,并用于智能协调和智能优化等方面[10].近年来尤其是随着模糊控制技术的引入和发展,针对复杂非线性大系统的各种控制问题得到了不少结果[11-18].这些结果根据控制器形式和设计方法的不同可大概分为两大类:一类以自适应控制技术为基础,通常被称作分散自适应模糊控制方法,可细分为分散直接自适应模糊控制、分散间接自适应模糊控制和分散混杂自适应模糊控制等几种类型,能够有效地随环境变化进行调节,实时学习被控对象的动态特性[11-13];一类以T-S模型为框架,利用线性矩阵不等式(LMI)技术得到一系列以LMI形式表示的闭环系统稳定性判据,最终完成分散模糊控制器的设计[14-18].近年来,大多数结果都是以自适应控制技术为基础发展而来[19-23],所涉及的理论结果并没有包含有限时间成分.而本论文利用FTS理论,针对复杂非线性大系统基于T-S模型设计了分散模糊控制器,具有一定的创新性,进而给出了保证闭环系统FTS的充分条件,该条件被表示为LMI形式,数值例子表明了所提出方案的有效性.
本文中R+表示正实数,Rn表示n维欧几里得空间,n×m表示n×m实矩阵,单位阵和零矩阵分别用I和O表示,表示对称矩阵中的对称块,标准符号><被用来表示矩阵正(负)定次序,max和min分别表示矩阵的最大特征值和最小特征值.
1 问题描述
复杂非线性大系统常常由多个子系统互联构成,较难建立精确的数学模型,在这里利用T-S模型来构造整个系统框架,对其进行数学描述.假设由J个互联子系统Sii=1,2,,J组成的复杂非线性大系统可由如下模糊规则形式表示.
被控子系统第l条规则
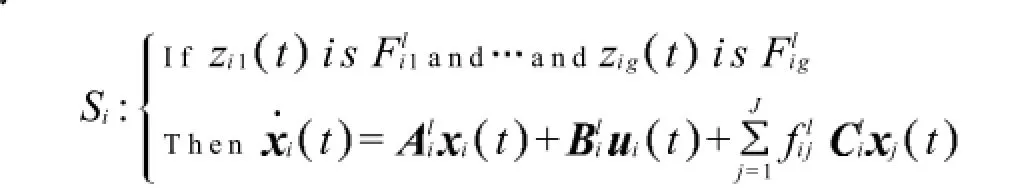

注释1:以上定义的表述形式来源于以前的结果[5],但在适用范围上有所扩展,在这里主要针对的对象是基于T-S模型的复杂非线性大系统.
注释2:Amato等提出的FTS概念本质上是有限时间有界的,这与一些已有的概念不同,例如文献[24],这些稳定性概念通常是相互独立的.
本研究的目的是设计一种分散模糊控制器,从而使基于T-S模型的闭环复杂非线性大系统满足定义1,下面将给出本文的主要定理和推论.
2 主要结果
本节将给出主要定理和推论,在开始证明主定理之前,首先给出一些必要的引理.


证明完毕.
3 数值例子
在这里给出一个数值例子用来验证所提出方案的有效性,类似于文献[15],考虑由3个子系统组成的互联非线性系统如下
子系统S1:
规则1:


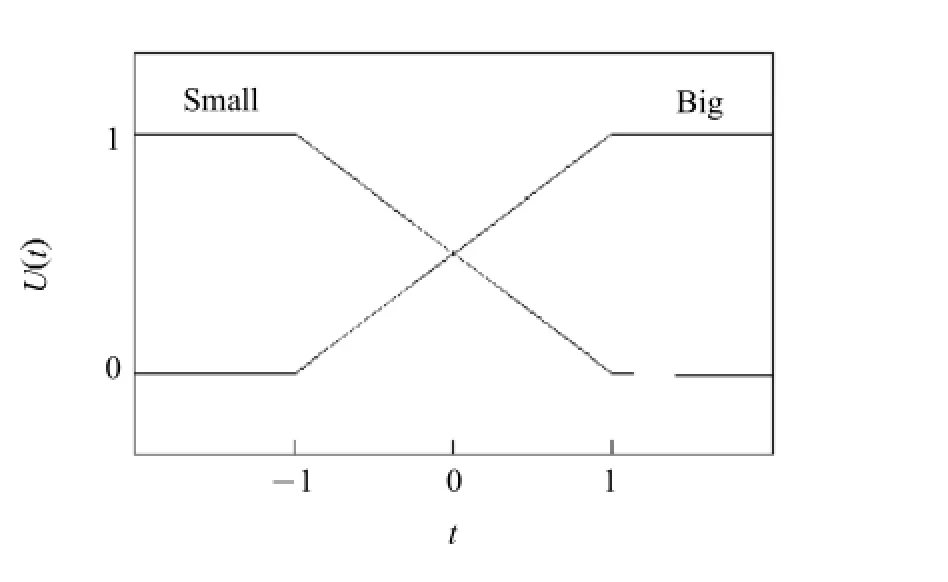
图1 隶属度函数Fig.1Membership functions
4 结论
本文基于T-S模型研究了复杂非线性大系统的有限时间分散控制问题,提供了分散控制的设计方案,给出了保证闭环系统FTS的充分条件.在未来的工作中将考虑系统的鲁棒性和更加实际的需求,例如:分段FTS问题,进一步拓展FTS的概念,将之更好的应用于生产实际中.
[1]GardnerMR,AshbyW R.Connectanceoflargedynamic(cybernetic)systems:criticalvaluesforstability[J].Nature,1970,228(5273):784.
[2]May R M.Will a large complex system be stable[J].Nature,1972,238(5364):413-414.
[3]Sandell J N R,Varaiya P,Athans M,et al.Survey of decentralized control methods for large scale systems[J].IEEE Transactions on Automatic Control,1978,23(2):108-128.
[4]Bakule L.Decentralized control:An overview[J].Annual Reviews in Control,2008,32(1):87-98.
[5]Amato F,Ariola M,Dorato P.Finite-time control of linear systems subject to parametric uncertainties and disturbances[J].Automatica,2001,37(9):1459-1463.
[6]Amato F,Ariola M,Cosentino C.Finite-time stabilization via dynamic output feedback[J].Automaitca,2006,42(2):337-342.
[7]Amato F,Ariola M,Cosentino C.Finite-time stability of linear time-varying systems:analysis and controller design[J].IEEE Transactions on Automatic Control,2010,55(4):1003-1008.
[8]AmatoF,CosentinoC,MerolaA.Sufficient conditionsforfinite-timestabilityandstabilizationofnonlinearquadraticsystems[J].IEEE Transactions on Automatic Control,2010,55(2):430-434.
[9]YangD,CaiKY.Finite-timequantizedguaranteedcost fuzzycontrolforcontinuous-timenonlinearsystems[J].ExpertSystemswithApplications,2010,37(10):6963-6967.
[10]万百五.大系统智能控制的进展[J].控制理论与应用,1994,11(1):118-121.
[11]ZhangTP,FengCB.Decentralizedadaptivefuzzycontrol forlarge-scalenonlinearsystems[J].FuzzySetsandSystems,1997,92(1):61-70.
[12]HuaC,GuanX,Shi P.Adaptivefuzzycontrolforuncertaininterconnectedtime-delaysystems[J].FuzzySets andSystems,2005,153(3):447-458.
[13]Tong S,Liu C,Li Y.Fuzzy-adaptive decentralized output-Feedback control for large-scale nonlinear systems with dynamical uncertainties[J].IEEE Transactions on Fuzzy Systems,2010,18(5):845-861.
[14]Wang W J,Leh L.Stability and stabilization of fuzzy large-scale systems[J].IEEE Transactions on Fuzzy Systems,2004,12(3):309-315.
[15]WangW J,LinW W.DecentralizedPDC for large-scaleT-S fuzzysystems[J].IEEE Transactions onFuzzySystems,2005,13(6):779-786.
[16]Tseng C S.A novel approachto H∞decentralizedfuzzy-observer-based fuzzy control designfor nonlinear interconnectedsystems[J].IEEE Transactions on Fuzzy Systems,2008,16(5):1337-1350.
[17]Zhang H,Feng G.Stability analysis and H∞controller design of discrete-time fuzzy large-scale systems based on piecewise Lyapunov functions [J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2008,38(5):1390-1401.
[18]ZhangH,DangC,LiC.DecentralizedH∞filterdesignfordiscrete-timeinterconnectedfuzzysystems[J].IEEETransactionsonFuzzySystems,2009,17(6):1428-1440.[19]Tong S C,Sui S,Li Y M.Adaptive fuzzy decentralized tracking fault-tolerant control for stochastic nonlinear large-scale systems with unmodeled dynamics[J].Information Science,2015,289:225-240.
[20]XiaoXS,WuLH.Decentralizedadaptivetrackingofinterconnectednon-affinesystems withtimedelaysandquantizedinputs[J].Neurocomputing,2014,141(SI):194-201.
[21]Huang Y S,Wang Z Y.Decentralized adaptive fuzzy control for a class of large-scale MIMO nonlinear systems with strong interconnection and its application to automated highway systems[J].Information Science,2014,274:210-224.
[22]TongS C,SuiS,LiYM.Adaptivefuzzydecentralizedcontrol forstochasticlarge-scalenonlinearsystemswithunknowndead-zoneandunmodeled dynamics[J].Neurocomputing,2014,135(SI):367-377.
[23]Sui S,Tong S C,Li Y M.Adaptive fuzzy decentralised output feedback control of pure-feedback large-scale stochastic non-linear systems with unknown dead zone[J].IET Control Theory&Applications,2014,8(7):488-502.
[24]Bhat P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal on Control and Optimization,2000,38(3):751-766.
[25]Boyd S,Ghauoi E L,Feron E,et al.Linear Matrix Inequalities in System and Control Theory[M].Philadelphia:SIAM,1994.
[责任编辑 代俊秋]
Finite-time decentralized control for complex nonlinear large-scale systems based on T-S model
YANG Dedong,CAI Yuzhu
(School of Control Science and Engineering,Hebei University of Technology,Tianjin 300130,China)
In this paper,we investigate the finite-time decentralized control problem of complex nonlinear large-scale systems via utilizing a fuzzy control approach.Based on T-S model,the mathematical description of complex nonlinear large-scale systems is given and the finite-time decentralized fuzzy controller is also designed.The sufficient conditions in terms of linear matrix inequality(LMI)are provided to guarantee the finite-time stability(FTS)of the closed-loop system.A numerical example shows the effectiveness of the proposed scheme.
large-scale systems;finite-time stability(FTS);decentralized control;fuzzy control;T-S model
TP273
A
10.14081/j.cnki.hgdxb.2015.03.001
1007-2373(2015)03-0001-07
2014-10-08
国家自然科学基金(61203076);天津市自然科学基金(13JCQNJC03500);河北省自然科学基金(F2012202100)
杨德东(1977-),男(汉族),副教授,博士.
数字出版日期:2015-06-16数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20150616.0922.002.html
