云闪测向定位算法
2015-07-05马舒庆庞文静蒲晓虎
梁 丽 马舒庆* 庞文静 蒲晓虎
1)(中国气象局气象探测中心,北京 100081)2)(重庆市气象信息与技术保障中心,重庆 401147)
云闪测向定位算法
梁 丽1)马舒庆1)*庞文静1)蒲晓虎2)
1)(中国气象局气象探测中心,北京 100081)2)(重庆市气象信息与技术保障中心,重庆 401147)
基于多站测向交叉算法,提出云闪侧向定位算法。根据各站仰角、方位角信息求解出各组闪电位置,由最大值和最小值约束条件剔除粗差较大的解后,引入加权运算得到较为准确的定位信息,再利用高斯牛顿迭代算法得到精准的云闪位置信息,从而实现云闪的三维定位。通过蒙特卡罗模拟方法,对算法进行评估,详细分析了站网多种因素对定位结果的影响。研究表明:该算法提高了定位精度,测向误差为1°时,4站站网误差低于500 m,站点越多定位精度越高,但综合考虑4站、5站站网为优,测向精度提高时,定位精度也随之提高;站网呈均匀布站方式优于T型等布站方式,均匀布站在实际中更具实用性。
测向定位; 云闪; 误差分析; 高斯牛顿迭代; 融合
引 言
随着气象、航空、航天及微电子领域的长足发展,闪电的超强、瞬间放电对其影响突显,尤其是云闪放电造成的危害,因此,精准、高效的云闪探测成为当务之急[1-8]。国内外闪电定位方法主要有时差法、测向法、测向时差法。时差法定位对孤立脉冲定位效果较好,但需要站点数量较多,且对连续脉冲定位较难[9];测向定位可以对同时发生的多个辐射源定位,定位精度较低。国内对测向云闪定位算法研究较少,基于提高测向法定位精度和实用性目的,本文主要探讨云闪三维测向定位算法,利用蒙特卡罗数学模拟方法,对算法进行评估,详细分析站网多种因素对定位结果的影响。
测向定位利用系统测得的仰角和方位角进行多站交汇得到目标位置。在复杂电磁环境下,测向定位结果很难在真实目标位置处相交,准确定位是多站测向定位的一个难点。文献[10]利用加权融合算法对三维目标进行定位,定位精度和稳定性优于文献[11]提到的传统定位方法,但稳定性和定位精度有待提高,文献[12]尝试利用牛顿迭代法对双信号台测向定位进行概位修正,该方法对初始值要求较高,容易出现不收敛情况。本文针对上述问题提出云闪测向定位(three-dimensional angle of arrival location,简称3D-AOA)闪电定位模型,利用多站测向定位,剔除不合实际的解,对解集合进行加权融合得到目标位置,再利用高斯牛顿迭代算法进行优化。实例计算表明,3D-AOA算法可以有效提高定位精度,合理布站时误差分布均匀,更具使用价值。
1 3D-AOA闪电定位模型
1.1 定位原理
3D-AOA闪电定位示意图如图1所示(以4站定位说明),S为闪电位置,A,B,C,D分别为站点位置。定位原理是根据各站点的方位角和俯仰角得到目标位置,剔除粗差解进行加权融合计算出被测目标的位置值,再利用高斯牛顿迭代算法进行位置的优化。

图1 闪电辐射源和站点位置示意图Fig.1 The sketch map of lightning radiation source and sites
1.2 定位方程的建立

(1)
(2)
i=1,2,…,n。
1.3 目标位置的解算
3D-AOA定位算法的步骤:①由n站的数据求解出n(n-1)个解;②剔除n(n-1)个解中不符合实际的解,得到优化解集合({Xm1},{Ym2},{Zm3}),其中,m1,m2,m3分别代表坐标x,y,z解的个数。m1,m2,m3均不大于n(n-1);③对优化解集合进行加权融合,得到位置向量估计值U=(X,Y,Z);④利用高斯-牛顿迭代算法进行位置优化。
由式(1)、式(2)可得定位公式,xij,yij,zij为位置坐标值:
xij=(yi-yj+tanθjxj-tanθixi)/
(tanθj-tanθi),
(3)
yij=[tanθjyi-tanθiyj+
tanθjtanθi(xj-xi)]/(tanθj-tanθi),
(4)
(5)
为了使定位更加精准,在解集合{xij,yij,zij},1≤i (6) (7) (8) 其中,K值由t分布的检验系数(可查表)确定,如果式(8)成立,则认为xr为粗大误差,剔除,否则保留。考虑实际中粗差一般为最值,先对解集合排序,判断最值是否为粗差,若不为粗差,停止粗差判断;若为粗差,逐一判断记录,若满足式(8)条件个数小于解个数一半则剔除,否则剔除粗差最大值。得到优化解集合{Xm1},同理,求解出{Ym2},{Zm3}。根据加权融合算法[10]得U=(X,Y,Z),权值取w时稳定性较高, (9) (10) (11) (12) 其中, (13) (14) (15) 高斯牛顿迭代算法的出发点是使残差平方和最小[14]。由加权融合得到初值U=(X,Y,Z),根据式(1)、式(2)反推各站仰角和方位角向量Pi(U)=[{θi},{φi}](1≤i≤n),各站接收的原始方位角、俯仰角P0=[{θi0},{φi0}](1≤i≤n),则残差为Ri(U)=Pi(U)-P0,残差的最小二乘形式为式(13),对L(T)进行一阶和二阶求导得式(17)、式(18),g1(U),g2(U)为L(U)的一阶和二阶求导公式。 (16) g1(U)=L(U)=A(U)R(U), (17) g2(U)=2L(U)=A(U)A(U)T+ (18) 其中,A(U)为式中P(U)对x,y,z偏导数的雅克比矩阵 (19) A(U(k))A(U(k))Th(k)= -A(U(k))R(U(k)), (20) L(U)近似为0。将加权融合得到的坐标值作为初始值,指定误差上限进行迭代运算得到最优位置解。首先,解算方程组,得到向量h(k)。然后,令U(k+1)=U(k)+h(k),若|U(k+1)-U(k)|<ε且|L(k+1)-L(k)|<ξ,则停止迭代,得到最优解Ubest=U(k+1)。 利用蒙特卡罗法分析定位误差,蒙特卡罗法是一种抽样技术,可求解具有随机性的不确定性问题。利用蒙特卡洛法求解雷电点位误差分布问题时,首先要确定模拟解算的次数(如N为1000次),对于每次模拟解算,随机产生一组探测站观测误差,然后通过定位算法求解出雷电的发生坐标,并进行误差概率分析。该方法可以理解为在某个特定点发生N次相同的闪电,探测网对其进行了N次解算。由于观测值中含有正态分布的随机误差,定位结果也将具有正态分布的误差。误差计算公式如下: (21) 点位估计量的均方根误差为 (22) 3.1 剔除粗差对算法精度的影响 设有4个探测站,站1(-100,100,0),站2(100,100,0),站3(100,-100,0),站4(-100,-100,0),坐标值表示该站与原点相对距离,单位为km[15]。假定利用4站探测(网内云闪)P1(10,10,10)和(网外云闪)P2(200,180,10)两处的雷电,到达各站的仰角和方位角信息均含误差。若不进行粗差剔除,直接测向交叉定位计算的原始值进行融合定位得P1估计值与实际值相距16.7440 km,P2估计值与实际值相距21.0756 km(表1)。进行粗差剔除后,融合计算得P1估计值与实际值相距1.8715 km,P2估计值与实际值相距为4.9265 km。基于加权融合测向定位算法(3D-AOA)计算得P1估计值与实际值相距3.7477×10-5km,P2估计值与实际值相距为 3.3782 km。数值表明,剔除粗差可以很好地改善定位精度。 表1 目标位置及不同定位算法处理的定位结果Table 1 Target location and positioning results of different-algorithm processing 3.2 测向误差对定位误差的影响 设有4个探测站,坐标同3.1节,站址误差为10 m,高度为10 km,角度测向误差在0.5°,1°,1.5°不同条件下,加权融合与3D-AOA两种算法的定位误差。由图2~图4可以看出,随着测向误差的增大,定位精度下降;同布站方式、同测向误差条件下,3D-AOA定位算法优于加权融合定位精度;同布站方式,站网内误差分布一致,站网外3D-AOA误差分布更均匀。 1.1 研究对象 选取了2017年1月至2018年5月安徽省肿瘤医院收治的脊柱转移性肿瘤(包括胸椎,腰椎转移癌)80例,其中男性43例,女性37例;年龄范围32~87岁,年龄(65.8±10.3)岁。通过计算机按照随机数字法分为氨甲环酸组和对照组,每组各40例。 图2 Δθ=Δφ=0.5°时,3D-AOA定位算法定位误差分布(单位:m,*为站点位置)Fig.2 Positioning error distribution for Δθ=Δφ=0.5°(unit:m,*denotes the location of sites) 图3 Δθ=Δφ=1°时,3D-AOA定位算法定位误差分布(单位:m,*为站点位置)Fig.3 Positioning error distribution for Δθ=Δφ=1°(unit:m,*denotes the location of sites) 图4 Δθ=Δφ=1.5°时,3D-AOA定位算法定位误差分布(单位:m,*为站点位置)Fig.4 Positioning error distribution for Δθ=Δφ=1.5°(unit:m,*denotes the location of sites) 3.3 布站方式对定位精度的影响 合理的站点布局可充分利用站点资源,提高定位精度、减少探测盲区。为分析布站方式对定位精度的影响,采用以下仿真条件:站网半径为75 km,站点以(0,0)点为圆心,各站测向误差为1°,站址误差为10 m。假设闪电辐射源高度为10 km,x方向范围为-200~200 km,y方向范围为-200~200 km。分析T型、菱形、Y型、随机布站4种布站方式,如图5所示。 图5 不同布站方式的3D-AOA定位算法定位精度(单位:m,*为站点位置)Fig.5 Different disposition way of positioning accuracy(unit:m,*denotes the location of sites) 由图5可知,定位误差小于500 m,均匀分布优于其他布站方式;站网内定位精度明显高于站网外;对称布站时,误差分布同样也具有对称性,且误差均匀性较好,实际应用中便于数据分析。 3.4 测站个数对定位精度的影响 在闪电定位系统中,探测子站数量是系统定位精度重要影响因子,同时也关系到最佳经济成本。采用以下仿真条件:站址误差为10 m,高度为10 km,不同个数的站点均以均匀方式环绕圆心,分析3站、4站、5站、6站定位的精度,如图6所示。 3站定位,网内定位精度较差,4站以上站网网内定位误差均小于500 m;随着参与定位站点的增加,定位精度逐步提高;小于5站时,站点增加,定位精度明显提高,6站定位,定位精度并不明显优于5站定位。所以在实际布站中,如果考虑经济因素,站点布置可以综合考虑。 3.5 基线长度对定位精度的影响 以上分析表明,站网内的定位精度均优于站网外的定位精度,为了检验基线长度对定位结果的影响,以5站均匀布站定位定位系统为例进行验证。 图6 不同测站数量3D-AOA定位算法定位精度(单位:m,*为站点位置)Fig.6 The positioning accuracy of different station number(unit:m,*denotes the location of sites) 仿真条件为站址误差为10 m,高度为10 km,基线长度(距中心点距离)分别为50,75,90,100 km(图7)。 由图7可以看出,同站点数量、站网结构和测向误差情况下,基线长度越大,站网定位精度越高;当基线长度达到100 km时,误差曲线没有短基线对称均匀,这是因为测向系统本身对定位距离的敏感性。不同基线长度对站网定位精度分析只是在理想情况下的理论分析结果,在实际站网确定基线长度时,应对仪器的探测性能、硬件测时精度、站网周围的地形地貌、探测网的具体用途等多种因素进行综合考虑。 图7 不同基线长度R的3D-AOA定位算法定位精度(单位:m,*为站点位置)Fig.7 Different positioning accuracy of the baseline length R(unit:m,*denotes the location of sites) 续图7 为提高闪电定位系统测向定位算法精度,本文提出3D-AOA定位算法,并对算法进行误差分析,得到如下结论: 1) 通过对4站站网网内和网外两点的云闪位置误差分析,剔除粗差可以明显提高定位精度。 2) 同布站方式同测向误差下,3D-AOA算法优于解融合定位精度,站网内误差分布一致,站网外3D-AOA误差分布更具均匀性。随着测向误差的增大,定位精度下降。 3) 由站网布局分析可知:均匀布站的定位精度分布均匀,且在测向误差为1°、站址误差为10 m时,定位误差小于500 m时,菱形布局最优。 4) 随着布站数量增加,定位精度随之提高;基线长度越长,站网内面积越大,站网内精度越高。 [1] Rustan P L,Uman M A,Childers D Q,et al.Lightning source locations from VHF radiation data for a flash at Kennedy Space Center.JGeophysRes,1980,85(C9):4893-4903. [2] 陈渭民.雷电学原理.北京:气象出版社,2009. [3] Rison W,Thomas R J,Krehbiel P R,et al.A GPS-based three-dimensional lightning mapping system:Initial observations in Central New Mexico.GeophysResLett,1999,26(23):3573-3576. [4] 张阳,张义军,孟青,等.北京地区正地闪时间分布及波形特征.应用气象学报,2010,21(4):442-449. [5] 张义军,周秀骥.雷电研究的回顾和进展.应用气象学报,2006,17(6):829-834. [6] 张义军,孟青,马明,等.闪电探测技术发展和资料应用.应用气象学报,2006,17(5):611-620. [7] 王学良,张科杰,张义军,等.雷电定位系统与人工观测雷暴日数统计比较.应用气象学报,2014,25(6):741-750. [8] 郭虎,熊亚军.北京市雷电灾害易损性分析、评估及易损度区划.应用气象学报,2008,19(1):35-40. [9] 张文娟,孟青,吕伟涛,等.时间差闪电监测网的误差分析和布局优化.应用气象学报,2009,20(4):402-410. [10] 佘玉莲,陈德生,谢君.VHF闪电定位技术评述.气象与环境科学,2008(5):55-58. [11] 刘李楠,赵晓萌.一种三维多站测向交叉定位算法.电子科技,2011,24(1):35-37. [12] 李洪梅,陈培龙.三维多站测向交叉算法及精度分析.指挥控制与仿真,2007(2):54-59. [13] 赵温波,曲成华,方青,等.雷达组网拟牛顿融合定位算法研究.现代雷达,2012,34(6):35-44. [14] 胡志祥.雷电定位算法和误差分析理论研究.武汉:华中科技大学,2012. [15] 吕帅华,孙秀琴,张占鹏,等.一种基于高斯-牛顿法的光电经纬仪交会测量算法.光电工程,2006,33(11):22-25. Direction-finding Location Algorithm of Cloud Flashes Liang Li1)Ma Shuqing1)Pang Wenjing1)Pu Xiaohu2) 1)(MeteorologicalObservationCenter,CMA,Beijing100081)2)(ChongqingMeteorologicalInformationCenter,Chongqing401147) Cloud lightning location is achieved by excluding solution with large gross errors to optimize initial solution, and joint constrained optimization of weighted integration and Gauss-Newton iterative algorithm based on the multi-station direction-finding cross-algorithm. The lighting position of each group is used as initial positioning solution, which is achieved according to elevation and information of azimuth. Initial solution is optimized through removing the solution with large gross errors by testing function of T-distribution, and then more accurate location information is obtained utilizing the weighted arithmetic. Cloud lightning location information is obtained accurately finally using Gauss-Newton iterative algorithm for constraint calculation. The algorithm is evaluated with the Monte Carlo simulation method, and then the influence of locating result is analyzed. Assuming the error of site layout is 10 m, the error of angle finding is 1°, the position precision is significantly improved using the algorithm of removing gross errors in four-station network simulation. The position precision of three-dimensiond angle of arrival loction (3D-AOA) is higher than integration solution under the same simulation conditions, which shows that the position precision is improved effectively by utilizing the weighted arithmetic and Gauss-Newton iterative algorithm. It shows that the accuracy of position is effectively improved and the deviation of four-station network is less than 500 m when the direction-finding error is 1°, and more stations lead to higher positional precision, but considering the balance of economic cost and precision, four- or five-station network is suggested. As the accuracy of direction-finding increases, the positional precision also increases. Analysis of different station network distributed shows that uniform distributed mode is better than others, the position precision of stations within a station network is clearly higher than stations out of the network. The error symmetry is convenient for analyzing data in practical application. Longer baseline leads to higher positioning accuracy of station network when the station number, station network structure and the direction-finding are fixed. Due to the sensitivity of finding system to the positioning distance, the error curve becomes less symmetrical when the baseline length reaches 100 km. The analysis on different baseline length of the station network positioning accuracy is only the theoretical result in the ideal case, a variety of factors such as instrument performance, detecting network, and hardware testing should be taken into comprehensive consideration in actual application. direction finding and location; cloud flash; error analysis; Gauss Newton iteration; fusion 10.11898/1001-7313.20150511 公益性行业(气象)科研专项(GYHY201106047) 梁丽,马舒庆,庞文静,等. 云闪测向定位算法. 应用气象学报,2015,26(5):618-625. 2014-12-29收到, 2015-05-27收到再改稿。 * 通信作者, email: msqaoc@cma.gov.cn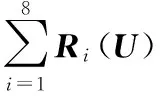
2 算法的误差分析
3 计算机仿真



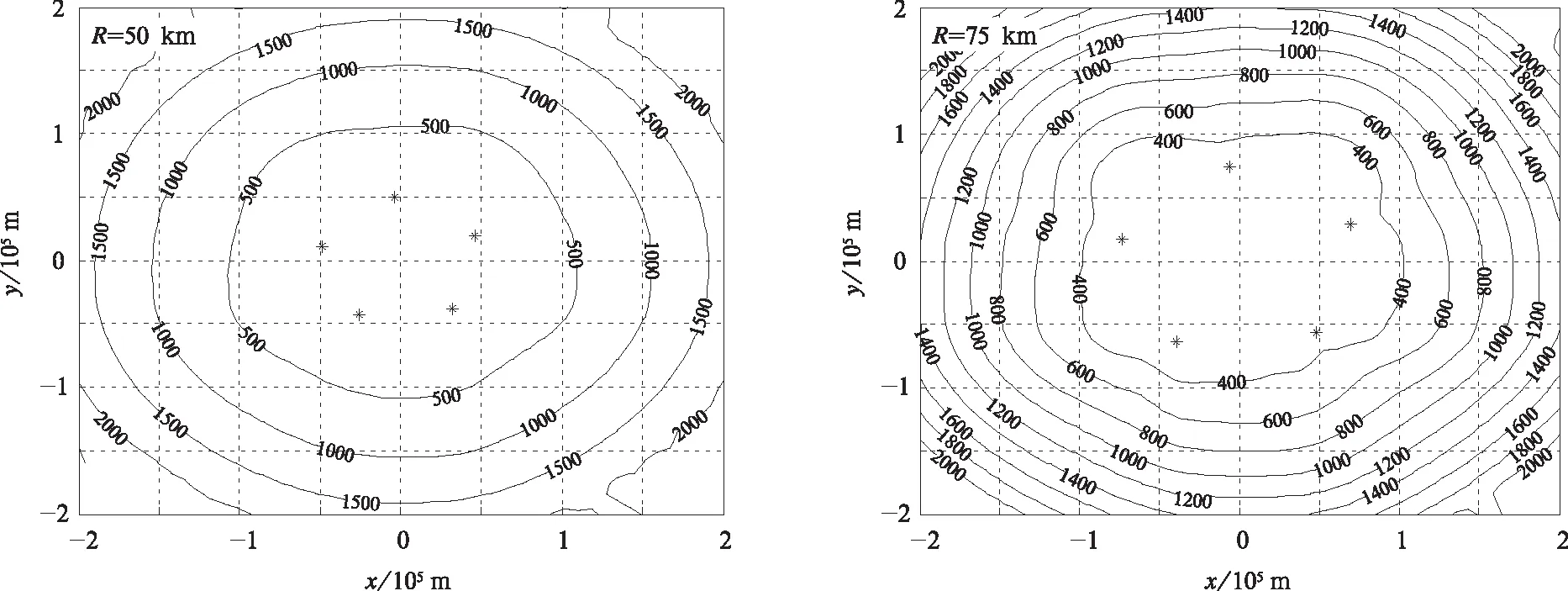
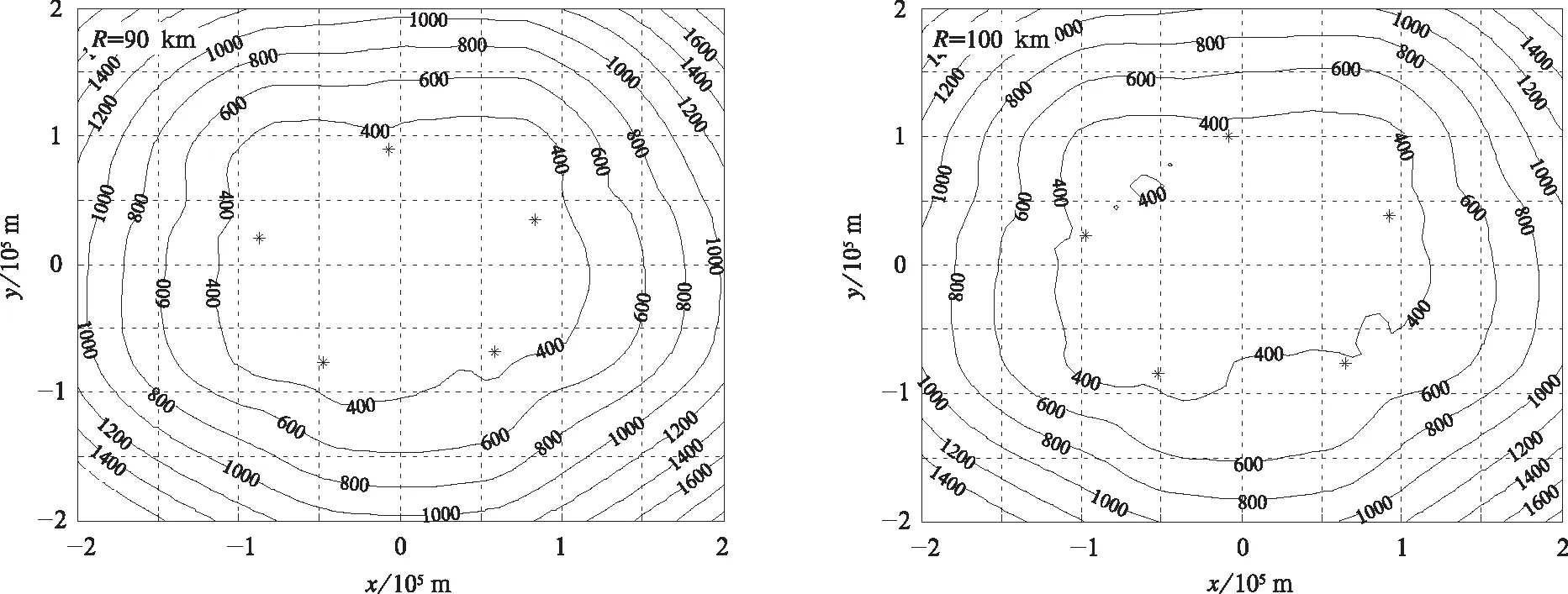
4 结 论
