一种多扭曲失真图像的质量评价方法

王春哲，李杰，李明晶，郭盼

一种多扭曲失真图像的质量评价方法

王春哲1，李杰2*，李明晶2，郭盼1

(1．长春理工大学研究生院，吉林长春130022; 2．长春大学电子信息工程学院，吉林长春130022)

针对现有评价方法不适合于多扭曲失真图像这一问题，本文展开了对多扭曲失真图像评价方法的研究。在分析图像的边缘信息和奇异值向量对视觉特征的表征能力的基础上，提出一种基于边缘信息奇异值分解的图像质量评价算法。首先，利用Sobel算子提取参考图像及失真图像视觉敏感的边缘信息，再对两图像的边缘信息进行奇异值分解，利用奇异值向量之间的夹角来描述失真图像的畸变程度。最后，采用LIVE数据库中的450张多扭曲的失真图像验证该文算法，并与MSE、PSNR、SSIM、CSSIM等算法进行了对比。实验结果表明，该文算法对多扭曲失真图像的质量评价具有更高的稳定性，主客观评价的一致性较传统评价方法更好。通过对比时间效率，该方法基本上满足实际需求，具有更高的适用性。

图像边缘信息;奇异值分解;图像质量评价

1 引言

在图像处理的诸多领域，都需要对被测试的图像质量进行评价［1］，评价方法分主观评价和客观评价。主观评价方法主要是通过观察者直接观察图像并按照某种标准对图像的质量做出评价，由于受到观察者本身诸多因素影响，且评价方法费时［2-3］，不适用于实时系统。客观评价方法一般采用一种数学模型来逼近主观评价，客观评价与主观评价结果的一致性是衡量客观评价方法优劣的重要指标。

根据对原始图像信息依赖程度，客观质量评价方法主要分为全参考、无参考和部分参考3种类型［4］。全参考评价方法是利用参考图像的全部信息，通过计算失真图像与参考图像之间的视觉感知误差值来衡量失真图像的视觉质量，主要有均方误差(MSE，Mean Square Error)、峰值信噪比(PSNR，Peak Signal to Noise Ratio)和结构相似度(SSIM，Structural Similarity Index Measurement Systemm)等方法［5-6］;无参考评价方法则不需要参考图像的任何信息，直接对失真图像做基于统计特性的描述，无参考评价方法能够满足实际需要，但由于没有任何参考图像的预知信息，无参考评价方法的难度较大［7］;部分参考评价方法是利用参考图像的部分信息或某些特征，评价失真图像的视觉感知质量，例如利用轮廓波变换的方向系数进行评价的方法(CSSIM，thecontourlettransformbased Structural Similarity)［7］。

目前客观质量评价方法中比较成熟的方法，大多是只针对某一种特定失真图像的评价算法［8］，但是一般人眼感受的图像信息要经过图像的获取、压缩、传输、接收等几个阶段，人眼最终获得的是一副具有多种失真的图像。2012年，Texas大学图像和视频工程实验室发布的多扭曲失真图像数据库(LIVE Multiply Distorted Image Quality Database)，为多扭曲失真图像评价算法的研究提供了标准的图像库，开创了多扭曲失真图像的质量评价研究的先河。本文在深入研究人眼视觉敏感理论及结构特征的基础上，用图像的边缘信息模拟人眼的视觉特性，以边缘信息的奇异值解释图像的结构特征，利用两奇异值向量之间的夹角描述多扭曲失真图像的畸变程度。实验结果表明，针对多扭曲失真类型的图像，该文方法与主观评价的一致性优于其他传统方法。

2 图像的边缘信息

由于图像的边缘信息包含了图像的大部分视觉敏感特征，因此可通过提取图像的边缘信息来评价图像的视觉感知质量。提取图像的边缘信息的算子很多，如Canny算子、LoG算子、Sobel算子等，考虑到算法的计算复杂度等因素［9］，选择计算复杂度低的Sobel算子进行边缘信息的提取。Sobel算子是一种利用局部差分寻找边缘的算子，算子不但能提供较为精确的边缘方向信息，而且对噪声具有很好的平滑作用。该算子包含两组3×3的矩阵，分别为横向及纵向，将与之图像做平面卷积，即可得出横向及纵向的亮度差分近似值。

若AM×N代表原始图像，Sx及Sy分别代表经横向及纵向边缘检测的图像，Sobel算子公式如下:

选择一个合适的阈值t，如果g(x，y)＞t，则认为这个像素点为边缘点［8］。

每个像素的梯度g(x，y)定义为:

3 图像的结构特征及奇异值分解

图像的奇异值包含了图像的大部结构特征，图像矩阵进行奇异值分解以后，奇异值表现出来的即为图像的结构特征。当图像有轻微的几何扰动时，图像的结构特征基本不变。

图像的奇异值分解是图像矩阵对角化的过程，若图像矩阵AM×N为实矩阵，则存在正交矩阵UM×M，VN×N，对角矩阵SM×N，有:

其中:UTU=I，VTV=I，r=rank(A)，S=diag(s1，s2，…，sr，0，…，0)。将这r个分量从大到小排列，即:s1≥s2≥…≥sr，s1，s2，…，sr即为图像A的奇异值，构成了A的奇异值向量［10］。

4 图像边缘信息的奇异值分解

从信息分布的角度分析，图像的结构特征与人眼视觉特性HVS(Human Visual System)不一致，因此图像的奇异值所表述的图像结构信息不能客观的反应图像的真实质量。由于人眼对图像的轮廓和边缘信息敏感［9］，因此本文采用对图像的边缘信息进行奇异值分解的方法解决此问题。

图像边缘信息奇异值分解的算法结构如图1所示，首先运用Sobel算子提取参考图像和失真图像的边缘信息，再分别对两图像的边缘信息进行奇异值分解，然后通过两图像边缘信息的奇异值夹角的大小来衡量失真图像的质量。两向量的夹角越小，表明两图像的相关程度越大，失真图像的视觉感知质量越好。

图1 边缘信息的奇异值分解(EQSVD)Fig．1Singular value decomposition of edge information

奇异值夹角定义［10］如下:

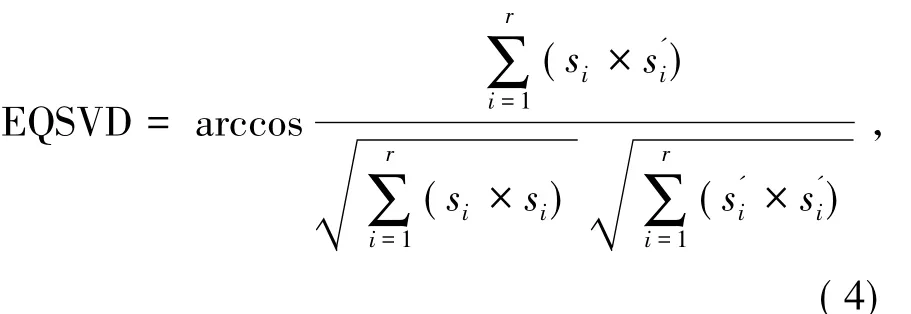
其中:si为参考图像奇异值，表示的是失真图的奇异值。

5 实验

5．1数据库及非线性回归函数的选取

实验采用美国Texas大学图像和视频工程实验室提供的多失真图像数据库［11］，该数据库中有15张标准参考图像和450张失真图像，图像分辨率为1 280×720。其失真图像由两部分组成，第一部分225张失真图像，由模糊图像经不同压缩倍率形成的多扭曲失真图像;第二部分225张失真图像，由模糊图像添加不同程度的噪声形成的多扭曲失真图像。该数据库中还给出了每张图像的主观差异评分DMOS(Difference Mean Opinion Score)值，DMOS值是图像的主观评价MOS(Mean Opinion Score)值与满分100分之间的差值，若DMOS值越小，图像的主观观测质量越好。

由于客观评分与主观评分存在非线性关系，为了衡量客观评价，需将客观评价结果进行非线性补偿，本文采用高斯函数对客观评价结果进行补偿，即:

其中:a1，a2，b1，b2，c1，c2是待测系数。

5．2方法实现

本文用来比较的客观评价方法有全参考型MSE、PSNR、SSIM方法和部分参考型CSSIM方法。计算数据库中450张失真图像客观测度MSE、PSNR、SSIM、CSSIM、EQSVD的客观成绩，并用式5将客观评分非线性映射到主观评分中，使用以下3个评价标准对客观预测和主观评价的一致程度进行评估。

(1)非线性回归下的客观评分与主观差异评分DMOS的均方误差均值(RMSE，Root Mean Square Error)，如式6。

(2)非线性回归下的客观评分与主观差异评分DMOS的相关系数(CC，Correlation Coefficient)，如式(7)。

式(6～8)中，xi表示非线性客观评分，yi表示主观差异评分DMOS值，x－为xi的均值，y－为yi的均值。

5．3实验结果及分析

首先对数据库中450张失真图像进行测试，将本文算法EQSVD与MSE、PSN、SSIM、CSSIM方法进行比较［7］，非线性拟合结果如图2、图3所示。

从图2的高斯非线性拟合结果可以看出，EQSVD方法的散点图最为集中，非线性拟合效果明显好于其他3种全参考评价方法。

(3)非线性回归下的客观评分与主观差异评分DMOS的绝对误差均值(MAE，Mean Absolute Error)，如式(8)。

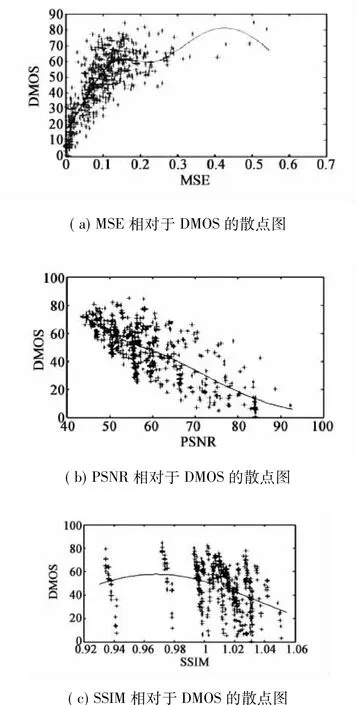
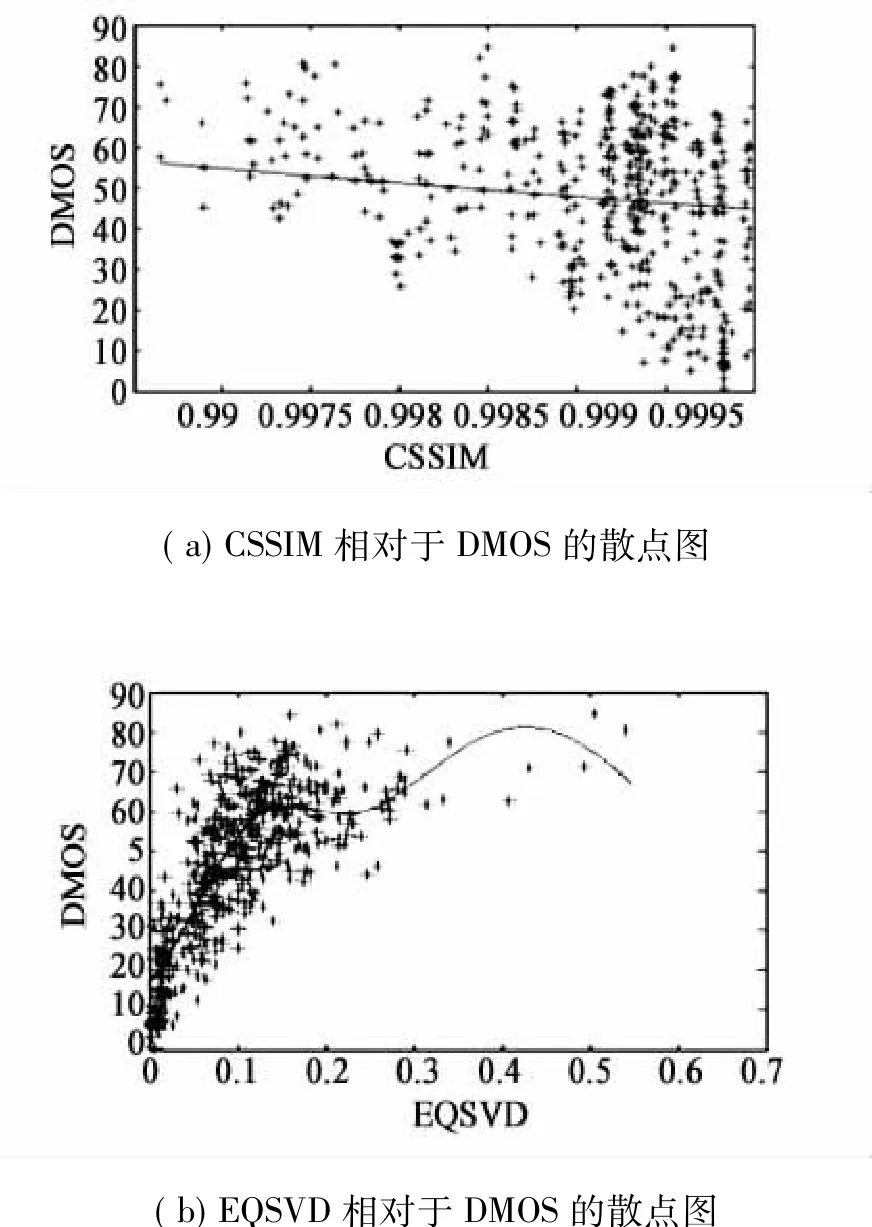
图3 部分参考评价模型相对于DMOS的散点图Fig．3Scatter of image quality assessment of reduced reference VS the DMOS

从图3的非线性拟合结果也可以看到，EQSVD散点图要比CSSIM方法散点图集中，非线性拟合结果也优于部分参考质量评价CSSIM方法。

为更精确分析所提算法性能，实验也采取RMSE、CC和MAE等3个评价标准比较了上述几种评价方法的效果，结果见表1。

从表1中数据可看出，EQSVD所对应的绝对误差均值MAE和均方根误差均值RMSE明显小于其他评价方法，EQSVD所对应的相关系数CC最大。因此，表1各指标说明了EQSVD算法不论与全参考评价方法MSE、PSNR、SSIM方法还是与部分参考评价方法CSSIM相比，与主观观测质量的一致性更好。

表1 客观评价方法的性能比较Tab．1Performance comparison of objective assessment methods

为验证本文算法的复杂度，本文设计了算法复杂度对比试验，实验中以数据库中一幅失真图像(1 280×720)为例，用于仿真的计算机CPU型号为Intel(R)Celeron(R)G550，工作频率为2.60 GHz，RAM为4 GHz。各种算法的运算时间比较结果见表2。

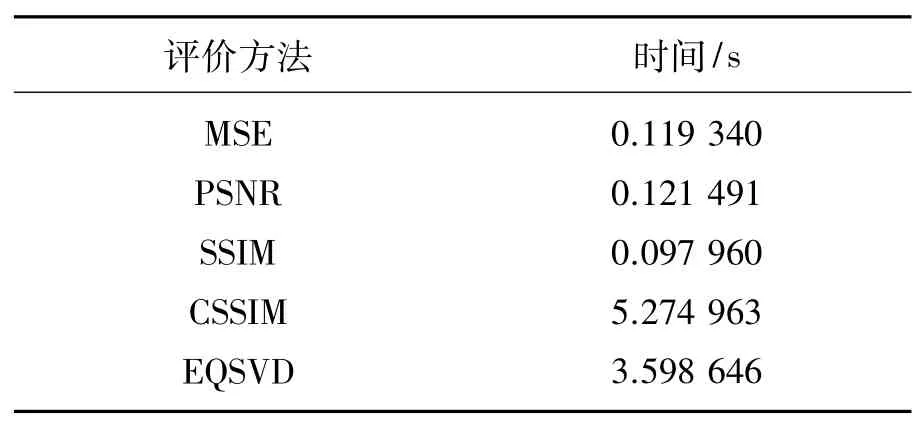
表2 运算时间比较Tab．2Comparison of computation time

从表2可看出，SSIM方法的速度最快，而CSSIM方法需要对轮廓波每个方向都进行SSIM运算，运算复杂程度最大，运行时间最长。本文设计的EQSVD方法运行时间优于CSSIM。

综合表1和表2指标，EQSVD方法性能比较其他方法更优越。

6 结论

提出一种基于边缘信息奇异值分解的EQSVD评价方法，通过Sobel算子对参考图像及失真图像的边缘信息进行奇异值分解，通过求其两图像的奇异值夹角分析两图像的相似程度。通过对多扭曲失真标准图像的仿真实验表明，EQSVD方法比MSE、PSNR、SSIM、CSSIM等算法具有更高的稳定性，主客观评价的一致性较传统评价方法更好。

［1］Lin W，Kuo C．Perceptual visual quality metrics:a survey［J］．Journal of Visual Communication and Image Representation，2011，22(4):297-312．

［2］赵梦，韦学辉．一种基于主成分分析法的图像质量评价方法［J］．杭州电子科技大学学报，2012，32(3):41-44．

Zhao M，Wei X H．An image quality evaluation method based on principal component analysis［J］．Hangzhou University of Electronic Science and Technology Journals，2012，32(3):41-44．(in Chinese)

［3］MaL，Li S N，King N N．Reduced-reference image quality assessment in reorganized DCT domain［J］．Signal Processing: Image Communication，2013，28(8):884-902．

［4］Li J，Wu K Z，Zhang X M，et al．Image quality assessment based on multi-channel regional mutual information［J］．AEUInternational Journal of Electronics and Communications，2012，66(9):784-787．

［5］KalitkinN N，Golovanov R V．Smoothed gradients criterion for image quality assessment［J］．Doklady Mathematics，2013，88(1):495-498．

［6］钱方，郭劲，孙涛，等．基于小波加权的激光干扰效果评估［J］．液晶与显示，2013，28(5):781-787．

Qian F，Guo J，Sun T，et al．Assessment of laser-dazziing effects based on weighted wavelet transforms［J］．Chinese Journal of Liquid Crystals and Displays，2013，28(5):781-787．(in Chinese)

［7］徐云生，尹东．一种基于Contourlet变换的图像质量评价算法［J］．电子技术，2010，47(7):23-26．

Xu Y S，Ying D．An image quality assessment algorithm based on contourlet transform［J］．Electronic Technology，2010，47 (7):23-26．(in Chinese)

［8］姚军财．基于人眼对比度敏感视觉特性的图像质量评价方法［J］．液晶与显示，2011，26(3):390-396．

Yao J C．Image quality assessment method based on contrast sensitivity characteristics of human vision system［J］．Chinese Journal of Liquid Crystals and Displays，2012，27(9):935-947．(in Chinese)

［9］Maria G M，Chaminda T H，Barbara V．Image quality assessment based on edge preservation［J］．Signal Processing: Image Communication，2012，27(8):875-882．

［10］骞森，朱剑英．基于奇异值分解的图像质量评价［J］．东南大学学报，2006，36(4):643-646．

Qian S，Zhu J Y．Image quality assessment based on singular value decomposition［J］．Journal of Southeast University，2006，36(4):643-646．(in Chinese)

［11］Sheikh H R，Wang Z，Cormack L，et al．LIVE image quality assessment database release 2［OL］．http://live．ece．utexas．edu/research/quality/live_multidistortedimage．htm．

Image quality assessment algorithm for multi-distorted image

WANG Chun-zhe1，LI Jie2*，LI Ming-jing2，GUO Pan1
(1．College of Electronic Information and Engineering，Changchun University of Science and Technology，Changchun 130022，China; 2．College of Electronic Information and Engineering，Changchun University，Changchun 130022，China)

Due to the problem that the existing method of objective quality assessment algorithm is not suitable for multi-distorted images，the quality assessment method for multi-distorted images was studied in this paper．On the basis of analyzing capability that the singular vector and edge information representing visual feature，an algorithm of image quality assessment based on the singular value decomposition of edge information was put forward．Firstly，the edge information of the reference image and distorted image which is sensitive to visual information was extracted by using the Sobel operator．Secondly，the singular value of the edge information of two image was decomposed，then the angle between the singular value was calculated to describe the quality of the distorted image．Finally，the algorithm applied in this paper are verified by more than 450 distorted images in LIVE Multiply Distorted Image Quality Database，and the algorithm was compared with the MSE，PSNR，SSIM，CSSIM method．Experimental results show that the algorithm is more consistent with human subjectscores and has greater stability for multi-distorted image than traditional methods．Through comparison with the time efficiency，the proposed algorithm can basically meet the practical demand，and the algorithm is more usability．

edge information of image;Singular Value Decomposition;image quality assessment

TP391．41

A

10．3788/YJYXS20153004．0681

王春哲(1989－)，男，吉林松原人，硕士生，主要从事图像质量评价及遥感图像处理技术的研究。E-mail: 1545208189@qq．com

李杰(1969－)，女，吉林白山人，教授，博士，硕士生导师，主要从事数字图像传感器技术和图像处理技术的研究。E-mail:lijie6915@foxmail．com

1007-2780(2015)04-0681-06

2014-07-11;

2014-09-02．

国家自然科学基金(No．61405191);吉林省科技厅自然基金项目(No．201215107);吉林省教育厅科研项目(吉教科合字［2013］第264号)

*通信联系人，E-mail:lijie1915@foxmail．com

李明晶(1977－)，女，吉林公主岭人，副教授，博士，主要从事图像融合处理技术的研究。E-mail:lmj5320510@ 163．com

郭盼(1989－)，女，吉林九台人，硕士生，主要从事图像融合和星图识别技术的研究。E-mail:963902263@ qq．com